高考易错题自测AB卷——不等式

广东 张红红

高考易错题自测AB卷
——不等式

广东 张红红

A卷

一、选择题

1．设集合P＝｛x｜－5＜x＜1｝，Q＝｛x｜（3－x）（x＋2）＞0｝，则P∩Q＝（ ）

A．（－5，3） B．（－2，1）

C．（－5，－2）D．（－2，3）

A．［－4，0］B．（0，4］

C．［0，4］D．［0，1］

3．不等式ax2＋8ax＋21＜0的解集为（－7，－1），那么a的值是（ ）

A．－3 B．1C．2 D．3

4．关于x的不等式mx2＋mx＋m＜1的解集为R，则实数m的取值范围是（ ）

5．不等式｜2x＋1｜－｜x－3｜＞2的解集是（ ）

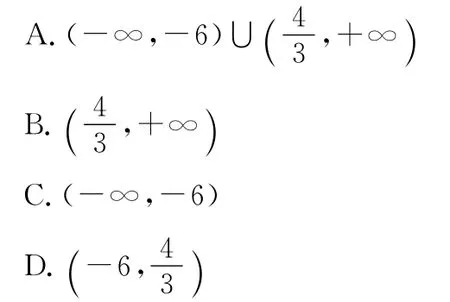
6．已知集合A＝｛x｜x2＋2x＜0｝，B＝则A∪B＝（ ）

A．（－∞，0） B．（－2，＋∞）

C．（－∞，－2）D．（－2，0）

A．［－1，2］

B．［－1，2）

C．（－∞，－1］∪［2，＋∞）

D．（－∞，－1］∪（2，＋∞）

8．若2a＋b＝3，则ab的最大值是（ ）

9．下列结论正确的是（ ）

A．－5B．－3C．1D．4

12．已知正数a，b满足a＋b－ab＋3＝0，则ab的取值范围是（ ）

A．［2，9］ B．（－2，1）

C．（1，＋∞）D．［9，＋∞）

二、填空题

B卷

一、选择题

A．8B．9C．12D．16

A．8B．9C．7D．6

A．－1B．0C．1D．2

A．［－2，2］ B．［－1，1］

C．［0，2］D．［0，1］

6．下列函数中，最小值为4的是（ ）

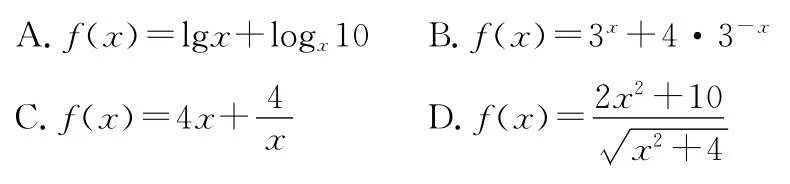
A．2 B．6C．9D．12

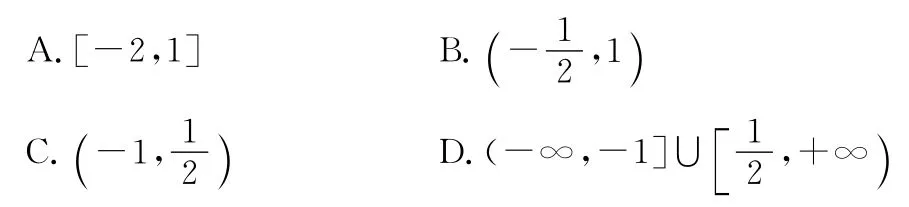
10．若方程x2＋ax＋2b＝0的一个根在（0，1）内，另一个根在（1，2）内，则的取值范围是（ ）

A．［－2，1］

B．（－2，1）

C．（－∞，－2）∪（1，＋∞）

D．（－∞，－2］∪［1，＋∞）

A．（－∞，0）

B．（2，＋∞）

C．（－∞，－1］∪［2，＋∞）

D．（－2，0）

12．某工厂第一年年底的产量为p，第二年的增长率为a，第三年的增长率为b，这两年的平均增长率为x，则有（ ）

二、填空题

14．二次方程x2＋（a2＋1）x＋a－2＝0有一个根比1大，另一个根比－1小，则a的取值范围是________．

15．已知实数a，b满足ab＝1，则a＋b的取值范围是________．

16．对一切实数，不等式x4＋（a－1）x2＋1≥0恒成立，则实数a的取值范围为________．

【参考答案与提示】

A卷

1．B 【解析】由（3－x）（x＋2）＞0，得－2＜x＜3，所以P∩Q＝（－2，1）．

【易错警示】注意（3－x）（x＋2）＞0对应二次函数y＝（3－x）（x＋2）的图象开口向下．

2．C 【解析】当a＝0时，得1＜0，该不等式的解集为空集，符合题意；当a≠0时，由解得0＜a≤4．综上所述，0≤a≤4．故选C．

【易错警示】错选B．错误原因：忽略了a＝0的特殊情况，误以为原式只能是一元二次不等式．

3．D 【解析】由题意a＞0且－7，－1是对应方程ax2＋8ax＋21＝0的两根，由根与系数的关系可得（－7）×，所以a＝3．

【易错警示】不能把握不等式解集区间端点和对应方程的根的关系．

【易错警示】错误一：没有将各段求解的结果与前提条件求交集；错误二：分类讨论之后，各段求解结果没有求并集．

6．A 【解析】A＝（－2，0），B＝（－∞，－1］，所以A∪B＝（－∞，0）．

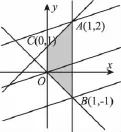
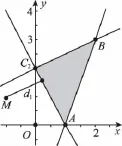
11．D 【解析】如图，目标函数z＝（x＋1）2＋（y－1）2的几何意义是表示可行域内任意一点（x，y）与定点M（－1，1）之间距离的平方．由图可知，最短距离即为点M到直线2x＋y－2＝0的距离d，易得d2＝．故选D．

【易错警示】错选B．忽略了表达式的几何意义是距离的平方．

12．D 【解析】由a＋b－ab＋3＝0得a＋b＝ab－3．因为

13．（－∞，1）∪（6，＋∞） 【解析】由原不等式移项得，等价于（6－x）（x－1）＜0，解得x＜1或x＞6．故原不等式的解集是（－∞，1）∪（6，＋∞）．

【易错警示】本题极易出现如下错解：两边同乘以x－1得3x＋2＜4（x－1），解得x＞6，所以不等式的解集为（6，＋∞）．警示：不等式两边同乘正数不改变方向，同乘负数改变方向．按以上错解思路，必须讨论x－1的符号．

B卷

【易错警示】先构造定值（常数），再进行常数代换．

【易错警示】利用基本不等式求最值时，必须满足“和为定值”或“积为定值”；所以，常常配凑成“和为定值”或“积为定值”．

3．B 【解析】将目标函数z＝mx＋y化成y＝－mx＋z后，如图所示平移到与可行域的边界AB所在直线重合时，截距z取得最大值，此时边界上的无穷多个实数对（x，y）使z＝mx＋y取得最大值，所以－m＝kAB＝，则，故选B．

【易错警示】“若有无穷多个实数对（x，y）”也可表达为“有无穷多个最优解”．y＝－mx＋z与另两条边界重合时，目标函数取最小值有无穷多个最优解，不合题意．

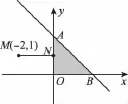
4．A 【解析】由x2＋4x＋y2－ 2y得表示如图所示区域上任意一点N（x，y）到定点M（－2，1）的距离d的平方与5之差．当距离d最小值2时x2＋4x＋y2－2y取最小值22－5＝－1，此时N（x，y）为（0，1）．故选A．

【易错警示】错误一：误认为最优解在可行域边界顶点处取得，将顶点O，A，B的坐标直接代入比较后得最小值0；错误二：将距离d的最小值2错当成x2＋4x＋y2－2y的最小值．

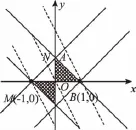
5．A 【解析】｜x｜＋｜y｜≤1表示正方形内部，xy≥0表示一、三象限内的点，综合两者得如图所示区域．将目标函数z＝2x＋y化成y＝－2x＋z后，平移直线y＝－2x使之过B（1，0）时z＝2x＋y取最大2，过M（－1，0）时取最小－2．故选A．

【易错警示】错选B．将目标函数z＝2x＋y化成y＝－2x＋z后，在与可行域的边界所在直线比较斜率后，没有把握好其倾斜角（倾斜程度）的大小．提示：当两角同为锐角或同为钝角时，斜率越大则倾斜角越大．

【易错警示】一是画错已知的不等式组表示的平面区域，特别是画图时的随意性，导致根据目标函数的几何意义确定最优解时位置出错；二是不能逆向应用z的最大值得到最优解，发现关系4a＋b＝9；三是不会将2a2＋b2转化为二次函数求最值．

9．C 【解析】已知不等式组表示的平面区域为图中的△ABC及其内部，三个顶点坐标分别为A（3，1），B（4，2），C（1，2）．将目标函数变形得y＝－kx＋z，当z最小时，直线的纵截距最小．结合动直线y＝－kx＋z绕定点A的“旋转分析”易得当斜率－k满足时，直线当且仅当经过点（3，1）时纵截距最小．故所求实数k的取值范围是．故选C．

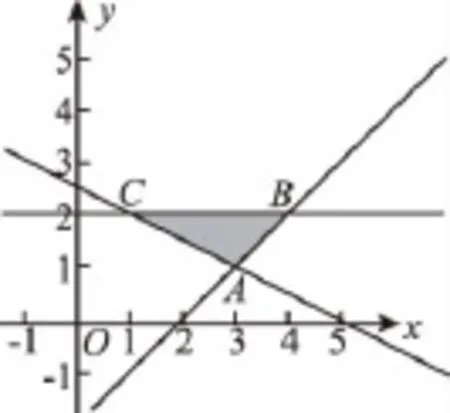
【易错警示】错选B，将动直线z＝kx＋y的斜率错当成k．

10．C 【解析】由已知画出二次函数f（x）＝x2＋ax＋ 2b的简图，可知可以看成是a－O－b坐标平面内可行域内的动点N（a，b）与定点A（－2，2）的连线的斜率．二元一次不等式组表示的平面区域如图阴影部分所示（不含边界）．因为kAB＝1，kAD＝－2，垂线AC的斜率不存在（可理解为无穷大），由斜率与倾斜角的关系可知，kAN∈（－∞，－2）∪（1，＋∞），故选C．

【易错警示】错误一：将区域边界画成实线，错选D；错误二：没有注意到NA的连线中有一条是倾斜角为90°的直线，错选B．

【易错警示】代入分段函数f（x）的表达式时，没有将自变量按区间进行讨论．

12．C 【解析】依题意得，该工厂第二年的产量为p（1＋a），第三年的产量为p（1＋a）（1＋b）．则p（1＋x）2＝p（1＋a）·（1＋b）．于是（1＋x）2＝（1＋a）（1＋b）≤．故选C．

【易错警示】错解：令x＋1＝t，则x＝t－1，则原式得y＝所以函数取最小值3．错误原因：基本不等式取等号时，），此时取不到等号．

14．－1＜a＜0 【解析】设f（x）＝x2＋（a2＋1）x＋a－2，由简图可知解得－1＜a＜0．

【易错警示】常见错解是直接求出两根的大小，将其分别与1，－1比大小，因得到的无理不等式求解烦琐而造成错误．对于二次方程根的分布问题，应根据条件画出简图，再从图形上找出某些特殊点的对应函数值的符号，有时还得联系对称轴的位置和判别式Δ的正负．

15．（－∞，－2］∪［2，＋∞） 【解析】当a＞0，b＞0时，a，当a＜0，b＜0时，（－a）＋（－b）≥，所以a＋b的取值范围是

【易错警示】忽视了“一正二定三相等”中的“正”的条件．

16．a≥－1 【解析】令x2＝t（t≥0），原式得t2＋（a－1）t＋1≥0恒成立．分离参数a，得（1－a）t≤t2＋1．当t＝0时，上式恒成立，此时恒成立，所以．而t＞0，因为，所以．所以1－a≤2，即a≥－1．综上所述，a≥－1．

【易错警示】错解成－1≤a≤3．将t2＋（a－1）t＋1≥0在［0，＋∞）恒成立误看成在R上恒成立．谨记：换元法换元时，产生“新元”，必须等价考虑新元范围．

（作者单位：广东省惠来县第一中学）