巧解选择题的一些妙招
广东 陈镇民
巧解选择题的一些妙招
广东 陈镇民
解答数学选择题的基本要求是准确、迅速、灵活,常用方法主要有直接法和间接法两大类.直接法是解答选择题最基本、最常用的方法,但高考的题量较大,如果所有选择题都用直接法解答,不但时间不允许,甚至有些题目的解答过程会变得繁杂.因此,我们还要研究解答选择题的一些技巧,掌握一些解选择题的特殊方法.总的来说,选择题属小题,解题的原则是:小题巧解,小题小做.
方法1 直接求解法
直接求解法就是由题干给出的条件出发,进行逻辑推理,直接得出结论.这种策略多用于一些定量性的问题,这是解选择题最常用的策略.这类题可直接从题设的条件出发,根据已知条件,相关公式、公理、定理、性质等通过准确运算、严谨的推理、合理的验证得出正确结论,然后与选项对照,从而作出相应的选择.
【例1】(2015·新课标卷Ⅰ文·3)已知点A(0,1),B(3, 2),向量
A.(-7,-4) B.(7,4)
C.(-1,4)D.(1,4)


【分析】本题主要考查三角恒等变换,由于角α的位置及其余弦值确定,所以属定量问题,适宜用直接求解法.

方法2 特例法
在求解数学问题时,如果要证明一个问题是正确的,就要证明该问题在所有可能的情况下都正确,但是要否定一个问题,则只要举出一个反例即可.基于这一原理,在解选择题时,可以通过取一些特殊数值、特殊点、特殊函数、特殊数列、特殊图形、特殊位置等对选项进行验证,从而可以否定和排除不符合题目要求的选项,再根据4个选项中只有一个选项符合题目要求这一信息,就可以间接地得到符合题目要求的选项,这是解选择题的特殊化策略.
【例3】(2010·安徽理·10)设{an}是任意等比数列,它的前n项和,前2n项和,前3n项和分别为X,Y,Z,则下列等式中恒成立的是( )
A.X+Z=2Y B.Y(Y-X)=Z(Z-X)
C.Y2=XZ D.Y(Y-X)=X(Z-X)
【分析】由于本题中的n∈N*,且四个等式中只有唯一成立,因而令n=1代入检验.
【解】令n=1,则X=a1,Y=a1+a2,Z=a1+a2+a3,代入四个选择支进行检验,可知选D.
【例4】(2010·新课标卷理·4)如图,质点P在半径为2的圆周上逆时针运动,其初始位置为),角速度为1,那么点P到x轴距离d关于时间t的函数图象大致为( )

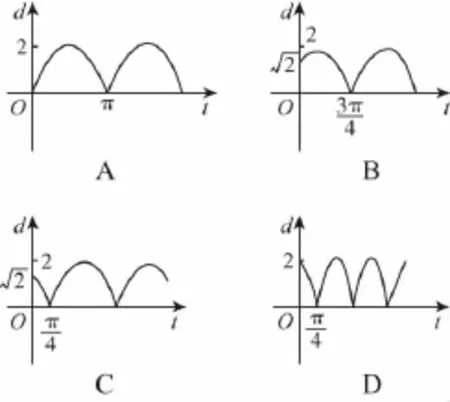
【分析】本题涉及质点的运动,可以结合质点运动的特殊位置与函数图象之间的联系来确定选项.
【例5】(2015·年新课标卷Ⅱ理·12)设函数f′(x)是奇函数f(x)(x∈R)的导函数,f(-1)=0,当x>0时,xf′(x)-f(x)<0,则使得f(x)>0成立的x的取值范围是( )
A.(-∞,-1)∪(0,1)B.(-1,0)∪(1,+∞)
C.(-∞,-1)∪(-1,0)D.(0,1)∪(1,+∞)
【分析】本题主要考查抽象函数与不等式的综合问题,因而可以通过构造符合题意的特殊函数来解决问题.
【解】令f(x)=x-x3,则f(-1)=0,当x>0时,xf′(x)-f(x)=x(1-3x2)-(x-x3)=-2x3<0,由f(x)>0,即x-x3>0,得x(x+1)(x-1)<0,解得x<-1或0<x<1.选A.
【例6】正四面体ABCD的顶点A,B,C分别在两两垂直的三条射线Ox,Oy,Oz上,则在下列命题中,错误的是( )
A.O-ABC是正三棱锥
B.直线OB∥平面ACD
C.直线AD与OB所成的角是45°
D.二面角D-OB-A为45°
【解】如图,正四面体ABCD的四个顶点分别为正方体的四个顶点,不难发现直线OB∥平面ACD不成立,故选B.
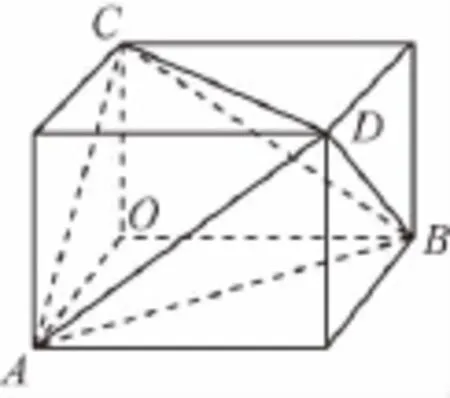
方法3 极限法
极限法可以归于直觉判断法,具体来讲,就是根据变量变化的趋势或极限的取值情况来发现结果,要求化动为静,在运动中寻找规律.从而可以避开抽象、复杂的运算,降低解题的难度,优化解题过程.

【分析】本题主要考查解析几何的定值问题,可以考虑选择点A或点B的极限位置,把动态问题转化为静态问题进行解决.

【例8】(2013·新课标Ⅱ理·12)已知点A(-1,0),B(1,0),C(0,1),直线y=ax+b(a>0)将△ABC分割为面积相等的两部分,则b的取值范围是( )


方法4 数形结合法
根据题设条件作出所研究的曲线或有关图形,借助几何图形的直观性作出正确的判断,这种方法叫数形结合法.有的选择题可通过命题条件的函数关系或几何意义,作出函数的图象或几何图形,借助于图象或图形的作法、形状、位置、性质,得出结论,图形化策略是以数形结合的数学思想为指导的一种解题策略.

【解】分别作出函数h(x)=x与函数g(x)=4sin(2x+1)的图象,要使函数f(x)在区间中不存在零点,即两函数h(x)与g(x)的图象没有交点,故选A.

【例10】(2014·新课标Ⅰ理·12)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )

C.6D.4
【分析】本题主要考查空间几何体的三视图,意在考查
考生的识图能力、空间想象能力及运算求解能力.
【解】如图,设辅助正方体的棱长为4,三视图对应的多面体为三棱锥A-BCD,最长的棱为故选C.

方法5 逆向思维法
在解选择题时,四个选项以及四个选项中只有一个是符合题目要求的都是解题的重要信息.逆向化策略是把四个选项作为首先考虑的信息,解题时,要“盯住选项”,着重通过对选项的分析、考察、验证、推断进行否定或肯定,或者根据选项之间的关系进行逻辑分析和筛选,找到所要选择的,符合题目要求的选项.
A.-2 B.2
C.-1 D.1
【分析】本题考查对新定义符号的理解及图象对称性,应考虑画图象,由于t的值未知,图象不容易确定,所以可以从选项入手.
【解】根据图象,t=-2时,函数f(x)的图象关于直线x=1对称(图①);t=2时,函数f(x)的图象关于直线x=-1对称(图②);t=-1时,函数f(x)的图象关于直线x=对称(图③).选D.
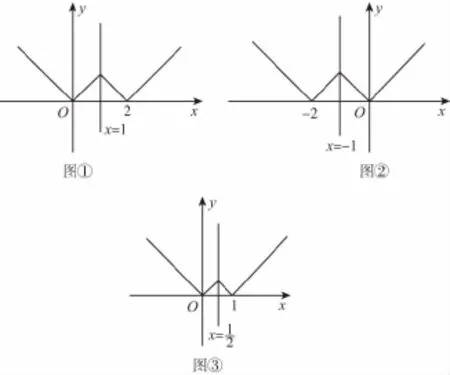
方法6 估算法
有些选择题由于条件的限制有时没必要进行精确运算,而只要依赖于估算就可以解决.估算实质上也是一种数学意识,它以正确的数理为依据,通过合理的观察、比较、判断、推理,从而做出正确的选择,因此,估算也是一种能力.
【例12】用1,2,3,4,5这五个数,组成没有重复数字的三位数,其中偶数的个数为( )
A.24 B.30
C.40D.60
【解】由1,2,3,4,5这五个数,组成没有重复数字的三位数共有A35=60个,其中偶数的个数不超过一半,故选A.
方法7 推理分析法
推理分析法是通过逻辑推断思维过程,分析各个选项之间的逻辑关系,从而否定干扰项,肯定正确选项的方法.
【例13】(2010·广东文·10)在集合{a,b,c,d}上定义两种运算和如下:
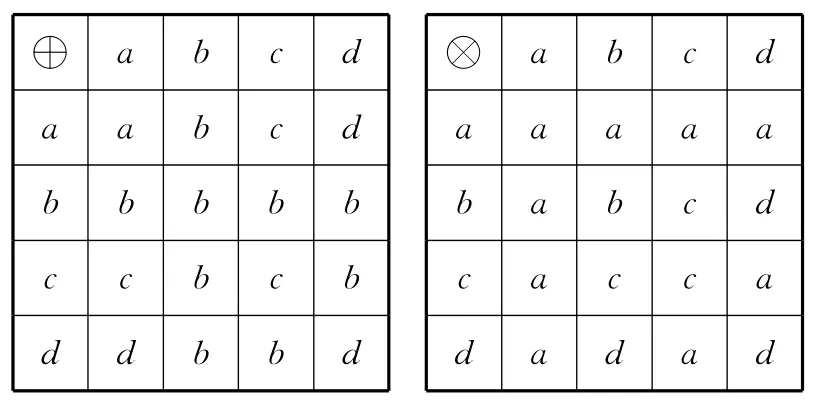
A.aB.b
C.cD.d
【分析】此类新定义问题,需要根据定义逐步进行推导.
【例14】(2015·广州市一模理·8)已知i是虚数单位,C是全体复数构成的集合,若映射f:C→R满足:对任意z1,z2∈C,以及任意λ∈R,都有f(λz1+(1-λ)z2)=λf(z1)+(1-λ)f(z2),则称映射f具有性质P.给出如下映射:
①f1:C→R,f1(z)=x-y,z=x+yi(x,y∈R);
②f2:C→R,f2(z)=x2-y,z=x+yi(x,y∈R);
③f3:C→R,f3(z)=2x+y,z=x+yi(x,y∈R);
其中,具有性质P的映射的序号为( )
A.①②B.①③
C.②③D.①②③
【解】设z1=x1+y1i,z2=x2+y2i,x1,y1,x2,y2∈ R,则λz1+(1-λ)z2=λx1+(1-λ)x2+[λy1+(1-λ)y2]i,对于①,f(λz1+(1-λ)z2)=λx1+(1-λ)x2-[λy1+(1-λ)y2],λf(z1)+(1-λ)f(z2)=λx1-λy1+(1-λ)x2-(1-λ)y2=λx1+(1-λ)x2-[λy1+(1-λ)y2],所以f(λz1+(1-λ)z2)=λf(z1)+(1-λ)f(z2),①是具有性质P的映射.
对于②,f(λz1+(1-λ)z2)=[λx1+(1-λx2)]2-[λy1+(1-λ)y2],λf(z1)+(1-λ)f(z2)=λx21-λy1+(1-λ)x22-(1-λ)y2=[λx21+(1-λ)x22]-[λy1+(1-λ)y2],显然,不是对任意λ∈R,f(λz1+(1-λ)z2)=λf(z1)+(1-λ)f(z2)成立,所以②不是具有性质P的映射.
结合选项,应选B.
【例15】如图,一个箱子的每个面都是矩形且边长都是整数,若它的主对角线XY=9,请问这个箱子的体积最大可能值是什么?( )

A.81B.90
C.108D.112

(作者单位:广东省广州市教育研究院)

