一种新的自适应动态网格优化算法

于　干, 周红志

(阜阳师范学院 信息工程学院，安徽 阜阳 236041)



一种新的自适应动态网格优化算法

于干, 周红志

(阜阳师范学院 信息工程学院，安徽 阜阳 236041)

摘要：针对动态网格优化算法(GEA)收敛速度较快，收敛精度不够理想，特别是解决多峰函数有可能会错过全局最优解的缺陷，提出了一种新的自适应动态网格优化算法.通过评估早熟收敛程度，将早熟收敛程度、函数的峰值与步长的变化联系起来，加入1个随机因子用以调整搜索范围，从而提高了算法的寻优效率.通过对典型的MP问题的测试，并与其他的动态优化算法比较，证明了算法的有效性.

关键词：动态网格优化算法；收敛程度；随机因子；有效性

动态网格优化算法(Gridding Evolutionary Algorithm，GEA)[1]是2007年由于干等人提出的一种基于网格节点的快速收敛算法.网格算法[2]的这种基于搜索网格节点的技术具有很强的定向搜索能力，主要体现为：算法能够按照设计好的搜索技术总是搜索当前几个较好的方向，这项技术能够保证算法不局限于只围绕一个点搜索，从而陷入局部最优，因此理论上它每次运行都能找到函数的全局最优解.

但网格优化算法的定向搜索特性在一定程度上限制了算法本身的随机性，优化结果的优劣很大程度上依赖于研究者给出的定向搜索信息，即所设置的一些参数如：演化步长、每代设定的较优解个数、每代搜索的网格点个数等.研究者通过对文献[3-4]的研究，借助其研究成果，设计了一种具有自适应能力的动态网格优化算法.本文提出的改进网格优化算法同传统的网格算法的主要不同在于：算法的自调节、自适应能力，也就是在不改变算法的定性特性的前提下，增加了算法的随机性，同时在种群初始化时也采用随机初始化方法.改进后的算法通过实验与文献[3-5]的研究结果进行比较，验证了算法的有效性.

1自适应动态网格优化算法(AD-GEA)

GEA的基本思想是：首先以待求解的函数变量区域的中心位置点为中心，依据设定好的步长值(步长值的初始值设置为函数变量区域长度的一半，标记为perlength)，根据函数的维数，将变量区域划分网格；依据适应值函数计算网格上各个网格节点的适应值，再统计适应值较好的几个点作为下一代演化的父代种群(较好点的个数需要根据函数的维数设定，一般设为4～8)；将步长值减少(一般减为原步长值的一半)，以新的步长分别在上一代保存的较好点的周围划分网格，分别计算每个网格上各个网格节点的函数值，分别找出几个较好个体暂存到较好个体集中，待所有网格点周围的较好个体搜索完成之后，筛选出较好的几个网格点作为下一代搜索种群；在新的搜索种群个体周围进行下一代的搜索.直到停止条件满足.

图1　GEA算法搜索过程

图1演示了GEA算法的搜索过程，算法每代只存放一个较好点.其中第一次以变量区间中心点为中心划网格，计算网格上所有网格点的函数值(空心圆点、中间的红色矩形点)，第一次找到的较好点假定为红色矩形点；第二次以红色矩形点为中心，以原步长的一般值再次划网格，计算网格上所有网格点的函数值(空心矩形点、红色圆点)，本次找到的较好点假定为红色圆形点；将步长再次减半，以红色圆形点为中心划分网格，计算、找出较好点假定为红色菱形点.依次搜索下去直到满足停止条件.

1.1网格优化算法特点及收敛性分析

从算法思想的描述可以得出算法的几个特性：

(1)算法从第一代设定几个网格点作为目前较好适应点，到以后每代产生几个最好适应点，算法都是围绕设定好的几个较好网格点周围展开搜索过程，这使得算法能够朝着潜在的最优解方向进行搜索.因此，算法不会盲目搜索，可以说这种搜索过程是一种确定性的搜索过程.

(2)每代设定好几个较好个体作为搜索的中心，且搜索每个较好个体以后都需要按照一定的规则在这个较好点的周围再筛选出几个较好的点暂存起来.当所有较好点按照此过程完成搜索以后，将所有暂存的较好解组合在一起筛选找出最好的几个点用于下一代搜索.这样保证了整个算法的搜索过程不会陷入到某一个最好点的局部搜索，避免了局部最优问题.

(3)算法的演化搜索过程中步长的设定一般都将步长逐次减半，也就是在当前搜索过程中在每个最好点的周围进行网格划分时所依据的步长为上一代所用步长值的1/2，在测试实验中函数的变量区域一般都不是很大.因此，在设置初始步长时通常设置为每维变量的区间范围的一半，通过这种快速的收缩过程使得算法能够很快地收敛到要搜索的函数全局最优解.

综上，网格优化算法具有：定向性、不易陷入局部最优、快速收敛等特性.

1.2自适应动态网格优化算法实现技术

基本网格优化算法依据步长快速变化而达到收敛目标，但这种技术也存在两个明显的缺陷：a)实际搜索过程中复杂的非线性行为在快速收敛的过程中，得不到有效的反映，导致收敛精度不够理想;b)网格优化算法每代都是围绕在设定好的几个较好解周围进行搜索，这种搜索过程解决单峰函数效果很好，但解决多峰函数有可能会错过全局最优解,因此它对于复杂问题的适应能力和调节能力都十分有限.

基于以上两个问题，本文在参考文献[3-4]中的自适应策略基础上，提出了一种动态随机调整策略，将早熟收敛程度、函数的峰值与步长的变化联系起来.基本思想是：解决单峰函数时，步长的变化依据早熟收敛程度设定.如果收敛程度较快，步长变化需慢些，以增加网格搜索范围，反之按照步长减半处理；解决多峰函数时步长变化依照单峰函数变化策略的同时增加1个随机因子.基本思想是将步长的变化与搜索过程的早熟收敛程度的指标联系起来，具体可按照下面公式进行：假设当前步长设为：Plen，下一代步长设为Nlen:

Nlen=w(t)Plen;

(1)

w(t)=1-(1+e-p)-1

(2)

式中，p为随机因子用于评价算法的收敛程度，p越小说明算法越趋于收敛.w(t)为步长变化权重值，由公式(2)看以看出，算法的步长变化权重值在(0，1)内变化，当p减小时(即算法趋于收敛)w(t)则增加，也就是扩大搜索范围，反之则减小.w(t)描述了在第t代的步长变化相对收敛速度的影响，w(t)取值大小可以调节GEA算法全局寻优能力与局部寻优能力，w(t)值较大，全局寻优能力强，局部搜索能力弱;反之，则全局寻优能力弱，局部寻优能力增强.恰当的w(t)可以提高算法性能，提高寻优能力，同时减少迭代次数.当GEA处于收敛状态时，需要增加搜索步长，从而增强GEA的全局寻优能力;当GEA处于全局搜索状态时，需要减小搜索步长，从而增强算法局部寻优能力.当早熟收敛程度的指标减小时，w(t)相应增加，增强了全局搜索能力；相反增大时，w(t)值将随之减小，增加局部搜索能力.

1.3自适应动态网格优化算法流程

综合以上基本原理，本文算法的基本流程如下：

a)种群初始化:在函数变量区间内随机产生M个点，通过研究证明M取值与函数的维数有关，当维数较低时M取值范围为5～10，当维数较高时M取值范围为20～50.具体做法是(以n维函数为例)：在函数变量区间内对任1个xi随意取值，形成1个点(x1,x2,x3，…,xn),作为当代搜索种群中的1个个体.然后按照此方法产生搜索种群的其他M-1个个体，M个种群个体必须包含函数变量区域中心点个体，形成初始种群Gen[M]；

b)设定初始步长:Pleni为函数变量xi区间长度值的一半；

c)在Gen[M]每个个体Mi周围分别实现：以当前步长Pleni为依据在每个变量区间上划分网格，任意一个变量都有xi，xi±Pleni，xi±2*Pleni等5种可能取值，然后所有xi可能取值在一起，随机的组合形成一组(x1,x2,x3，…,xn)，统计这些点的函数适应值，比较后选出n个较好的点(n值一般取3～5)，放入较好种群Betterpoint[n*M]中；

d)产生下一代演化种群个体集：在步骤c完成的基础上，在Betterpoint[n*M]中选出M个适应值较好点，从而得到BestPoint[M]作为下一代种群Gen[M]；

e)计算算法的收敛程度:BestPoint[M]中M个点的函数适应值最优解与实际最优解的的差值作为计算依据，当差值小于0.001时，p值取较小值取值范围为(0～0.5)，反之p取较大值取值范围为(0.5～1.0)；

f)计算下一代步长：利用公式(1)、(2)计算出下一代步长Plen；

g)演化搜索过程终止判定：若满足算法终止条件则停止搜索过程；如不满足则转至步骤b.通常算法的终止条件设置为：演化代数满足要求或BestPoint[M]所有个体的适应值最大差值<=0.000 01.

2仿真实验

2.1实验函数

为对本文算法的思想进行有效性的验证，本文测试了MP(MovingPeak)问题[6](由Branke提出)，函数形式如下:

(3)

式中，X(t)、Wi(t)、Hi(t)分别表示时刻t时峰i的位置、宽度和高度，峰的个数用m表示，n代表函数的维数，函数问题的一个解用X=(x1,x2,x3，…,xn)表示，每个解X的适应值为F(X，t).Hi(t)、Wi(t)和X(t)的变化过程为：

Hi(t)=Hi(t-1)+α·β

Wi(t)=Wi(t-1)+β·δ

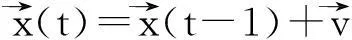
α和β分别表示与函数的高度和宽度相关的惩罚因子，σ是一个用于增加函数随机性的高斯变量，同时为了控制峰的变化方向增加了一个随机矢量V.

函数的维数、峰每次变化所移动的距离及函数峰的个数均是MP函数的决定性参数.因此，AD-GEA的实验将主要在这几个方面与文献[3-6]中所提到的GEA、SOS、AD-CPSO算法进行比较.

2.2实验结果

表1给出了在本文的实验中函数的所有初始化参数.其中f是函数变化的频率,A表示函数自变量变化范围，H表示峰高的变化范围，W表示峰宽的变化范围,I表示所有峰的初始化高度，M为所有实验中测试函数的变化次数.

表1　实验函数的所有初始化参数

表2　峰移距离S不同,GEA和SOS算法所得到的平均误差值

表3　峰数n不同时,GEA和SOS算法所得到的平均误差值

上述实验结果(表2、表3)表明：在解决动态函数优化问题方面，AD-GEA能够很好地解决动态函数优化问题,无论是演化代数还是误差值均明显好于文献[3-6]中所提到的GEA、SOS、AD-CPSO算法.特别是在求解低维数的优化函数时,GEA的快速收敛性和精确性优势更加明显.

3结语

针对GEA算法收敛速度较快，收敛精度不够理想，特别是解决多峰函数有可能会错过全局最优解的缺陷，本文提出了一种新的自适应动态网格优化算法.通过评估早熟收敛程度，将算法的搜索过程与收敛程度结合起来，加入一随机因子用以调整搜索范围，从而提高了算法的寻优效率.

自适应动态网格优化算法和别的优化算法相比，具备以下不同点：

1)算法并不是记忆存储过的所有有效信息，它只是将当前一代比较有效的结果用于下一代的优化；

2)算法并不是在这个优化空间不停地搜索，而是将搜索空间划分成多个区域，依据当前的优化信息在最优希望的区域进行搜索.

需要指出的是，本文算法在解决多维、高峰函数优化问题时，如何进一步减少每代搜索的个体个数，将是下一步研究的重点.

[参考文献]

[1]吴亚丽,徐丽青.一种基于粒子群算法的改进多目标优化算法[J].控制与决策,2012,27(8)：1127-1132.

[2]于干，李长河，康立山.一种新的基于网格的函数优化算法[J].计算机应用，2007，27(7)：1760-1759.

[3]WANG YS,AI JB，SHI YJ，et al.Cultural- based particle swarm optimization algorithm[J].Journal of Dalian University of Technology,2007,47(4):539-544.

[4]任圆圆,刘培玉,薛素芝.一种新的自适应动态文化粒子群优化算法[J].计算机应用研究，2013,30(11):3240-3243.

[5]于干，康立山.基于网格的一种新的动态演化算法[J].计算机应用，2008，28(2)：319-322.

[6]BRANKEJ,KAUFLERT,SCHMIDTC,et al.A multipopulation approach to dynamic optimization problems[C]∥Adaptive Computingin DesignandManufacturing.NewYork:Springer-Verlag,2000:299-308.

[责任编辑马云彤]

A New Adaptive Dynamic Gridding Evolutionary Algorithm

YU Gan， ZHOU Hong-zhi

( School of Information Engineering, Fuyang Teachers College, Fuyang 236041, China )

Abstract：In view of the shortage of fast convergence speed of optimization algorithm for dynamic Gridding Evolutionary Algorithm (GEA), unsatisfactory convergence precision and especially the defect in missing the global optimal solution when solving multimodal function, a new optimization algorithm for adaptive dynamic gridding was proposed in this paper. It improves the optimization efficiency of the algorithm by evaluating the degree of premature convergence, linking the degree of premature convergence and the change of peak and step of function and adding a random factor to adjust the search scope. It proves the effectiveness of the algorithm through the tests on the typical MP problem and comparisons with other dynamic optimization algorithms.

Key words：dynamic gridding evolutionary algorithm; convergence degree; random factor; effectiveness

中图分类号：TP393.028

文献标志码：A

作者简介：于干(1982—)，男，安徽亳州人，阜阳师范学院信息工程学院讲师，硕士，主要从事智能计算与智能优化研究.

基金项目：安徽省自然科学一般项目(2014FXSK01)；安徽省自然科学项目(2015FXTZK03)

收稿日期：2015-04-30

文章编号：1008-5564(2016)01-0048-04