一种基于泰勒级数多元变量展开模型定位算法

刘承鹏， 夏　斌， 谢　楠， 彭荣群

(山东理工大学 计算机科学与技术学院， 山东 淄博 255049)



一种基于泰勒级数多元变量展开模型定位算法

刘承鹏， 夏斌， 谢楠， 彭荣群

(山东理工大学 计算机科学与技术学院， 山东 淄博 255049)

摘要：为了提高无线传感器网络节点定位精度，构建了增加未知节点与未知节点间的距离信息的泰勒级数多元变量展开定位模型.在对该算法的求解过程中，首先利用最大似然估计法得到未知节点的初始位置，再运用加权最小二乘法计算其最优值作为未知节点的估计位置.仿真测试了不同距离测量误差和已知节点数目对定位误差的影响，以及算法的累计分布函数.结果表明，该算法能够有效提高节点定位精度.

关键词：泰勒级数多元变量展开； 定位模型； 最大似然估计； 无线传感器网络

在无线传感器网络诸多节点定位算法中，泰勒级数展开法[1-3]以其收敛速度快、顽健性强、求解精度高等优点，成为一种常用的节点定位方法.文献[4]提出了一种基于最小二乘法和泰勒级数展开的协同定位算法，该算法将最小二乘法获得定位结果作为泰勒级数展开法的初始值，然后进行泰勒级数展开，从而获得二者协同的定位结果.文献[5]提出一种基于Taylor和Kalman的室内协同定位方法.先利用Chan与Taylor二者协同的方法对位置信息进行估算，取符合条件的测量数据，再用Kalman法计算定位结果，将二者的结果进行比较，对符合条件的定位结果进行处理，最终完成定位.但是，这些定位算法都是采用传统的泰勒级数展开定位模型结合其它不同的算法进行定位.传统泰勒级数展开法仅考虑了位置已知节点与未知节点之间的距离，位置信息不充分，无法完成更精确的节点定位.

鉴于此，本文增加未知节点与未知节点之间的距离信息，构建了新的泰勒级数展开模型，即泰勒级数多元变量展开定位模型.基于此模型，提出一种新的节点定位算法.该算法首先利用最大似然估计法[6-9]得到位置未知节点的初始值，再根据泰勒级数多元变量展开定位模型进行迭代.为了衡量算法的性能，通过仿真验证了该算法的有效性.

1泰勒级数多元变量展开定位模型

在二维空间中，随机均匀布放N+M个传感器节点.其中，N为未知节点的数目，M为已知节点的数目.无线传感器网络通过TOA技术[10-11]获得测量值，然后计算得出所有节点间的距离测量值：

(1)

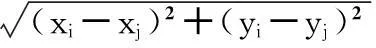
(2)

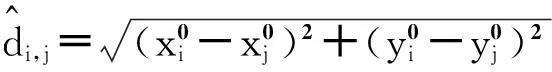
将(2)式移项整理，得到如下形式：

(3)

式(3)可以简记为新定位模型：

S=TΔ+E

(4)

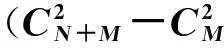
2新定位算法

2.1算法描述

新算法的求解过程为，先用最大似然估计法得出未知节点位置的初始值后，再采用加权最小二乘法[12-15]计算其位置的估计值.详细步骤如下：

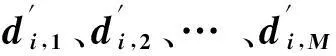
(5)

将方程组(5)的前M-1项减去第M项，得到如下方程组：

(6)

将(6)式移项整理，后得到如下形式：

AX=b

(7)

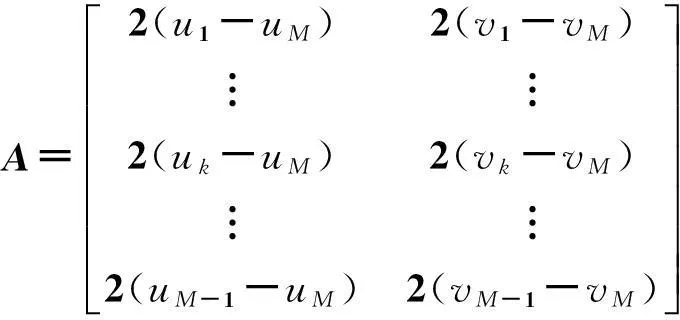
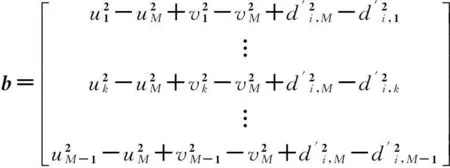
利用标准最小二乘法，可得X点的估计坐标:

(8)

(2)根据求解出的所有未知节点位置的初始值， 由公式(4)得到泰勒级数多元变量展开定位模型S=TΔ+E.

(3)利用加权最小二乘法求解位置偏差：

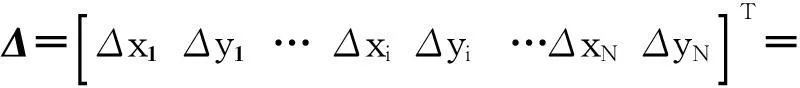
(TTW-1TT)-1TTW-1S

(9)

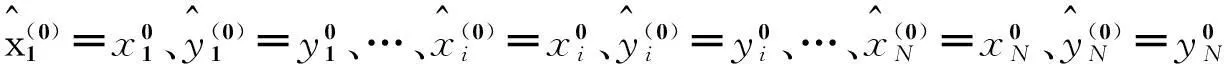
(10)

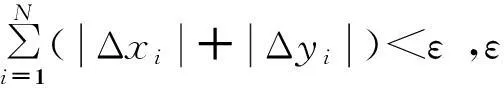
2.2算法复杂度分析

新算法的泰勒级数多元变量展开定位模型中增加了未知节点与未知节点之间的距离，提高了计算量.表1给出了三种算法的时间复杂度.

表1三种算法复杂度对比

算法时间复杂度最大似然O(N2Mh)最大似然+传统泰勒O(N2Mh)+O(NM)新算法O(N2Mh)+O(N4)

表1中，N为未知节点数目，M为已知节点数，h为迭代次数.从表1中可以看出，新算法复杂度是三者中最高的.新算法时间复杂度虽有所增加，却获得了更高的定位精度.

3仿真结果与分析

为了验证基于泰勒级数多元变量展开定位算法的有效性，利用工具Matlab对新算法进行仿真，并与最大似然估计法、最大似然估计结合传统泰勒级数展开算法进行对比分析.仿真参数为100m×100m 的平面区域，随机均匀布放20个未知节点.独立仿真1 000次.假设距离测量误差服从高斯分布N(0,σ2).为评价定位算法性能，用定位结果的均方根误差计算定位误差，表示为

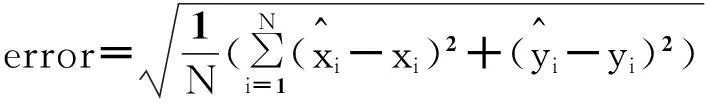
(11)

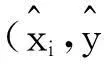
3.1距离测量误差对定位误差的影响

在距离测量过程中势必会产生误差，因此，测量误差对定位误差的影响是衡量定位算法性能的重要指标.图1给出的是三种定位算法的定位误差随着测量误差方差变化曲线图.仿真条件为已知节点数目M=5，且随机均匀布放于平面仿真区域.从图1中可以看出，其定位误差均随测量误差的升高而升高.但是新算法的定位误差明显小于其它两种算法，这是因为在新算法中采用的是泰勒级数多元变量展开，增加了未知节点与未知节点之间的距离信息，而传统泰勒级数展开并未考虑这一点.由此，新算法降低了定位误差，提高了定位精度.另外随测量误差的变化，新算法曲线斜率(大于零)更小，这说明新算法在距离测量误差变化跨度较大时，定位误差变化不大，较其它两种算法能更好地降低测量误差对定位误差的影响.

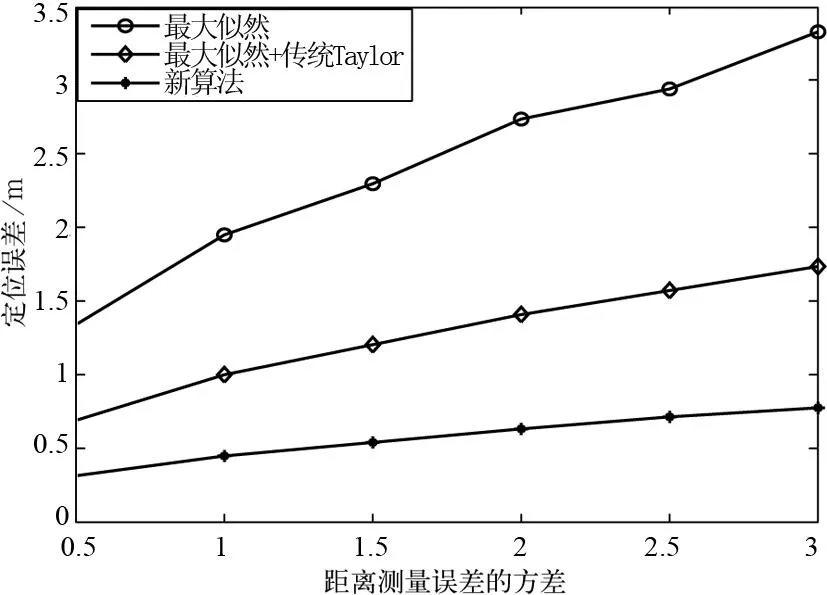
图1　定位误差随距离测量误差的变化图

3.2位置已知节点的数目对定位误差的影响

图2是当距离测量误差的方差σ2=1.5时，已知节点数目对三种算法定位误差的影响曲线.横轴表示已知节点数目，纵轴表示定位误差.从图2中可以看出，未知节点数目不变的情况下，三种算法的定位误差均随已知节点数目增加而减小.新算法的斜率(小于零)较大，说明新算法较其它两种算法的定位误差受已知节点数目影响较小.新算法在达到相同定位精度时可以降低已知节点的使用数目，从而节约成本.

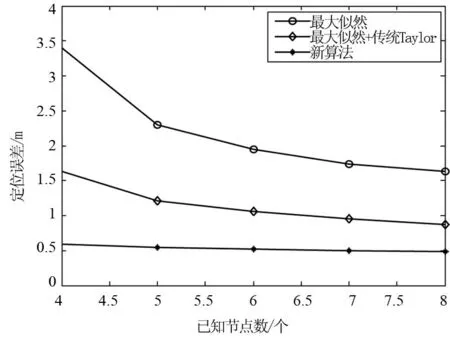
图2　定位误差随已知节点数目的变化图

3.3定位误差的累积分布函数

图3给出了距离测量方差σ2=1.5时，三种算法定位误差累积分布函数曲线图.横坐标表示定位误差，纵坐标表示定位误差小于横坐标值的概率.从图3可以看出，在90%的累积分布点，最大似然估计法、最大似然估计结合传统泰勒级数展开算法、新算法的定位误差在1.83m、1.23m、0.81m以内.实验数据显示，在距离测量误差相同的条件下，新算法的定位精度明显优于其它两种算法.

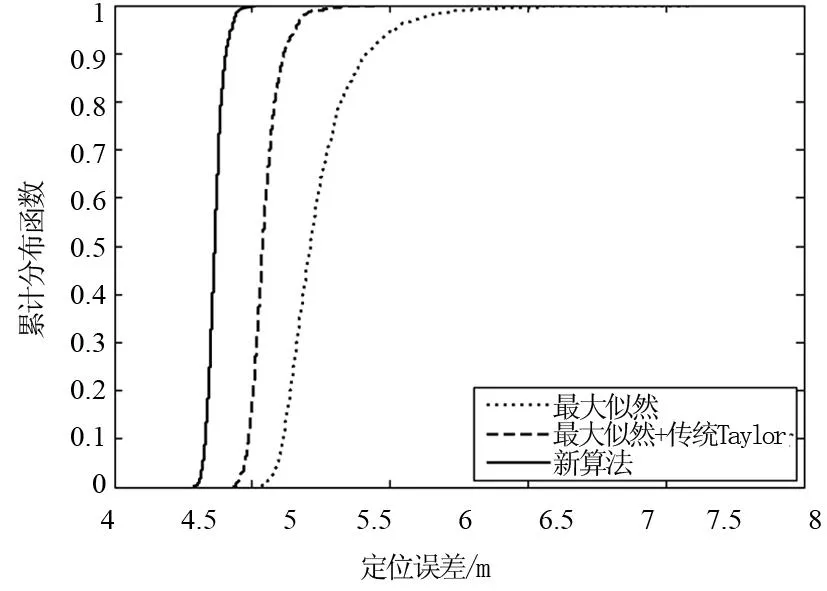
图3　定位误差的累积分布函数图

4结束语

文中建立了新的泰勒级数多元变量展开的定位模型.并在该模型基础上，提出了一种新的定位算法，将最大似然估计法与泰勒级数多元变量展开法相结合，充分发挥二者所长，使算法的整体定位性能更优.仿真结果表明，新算法能够较好地降低距离测量误差对定位精度的影响.但该算法是基于距离测量信息已知的条件下进行的，而部分距离测量信息未知的情况有待继续研究.

参考文献:

[1] Foy W H. Position-location solutions by Taylor series estimation[J]. IEEE Transactions on Aerospace Electronic Systems, 1976, AES-12(3):187-194.

[2]熊瑾煜, 王巍, 朱中梁. 基于泰勒级数展开的蜂窝TDOA定位算法[J]. 通信学报, 2004, 25(4):144-150.

[3]刘春红, 战美, 陆萍萍. 基于Taylor级数展开的改进定位算法研究[J]. 无线电通信技术, 2012, 38(6): 48-51.

[4]冯慧昭, 张正平, 秦水介. 一种基于最小二乘法和Taylor级数展开法的协同定位算法[J]. 通信技术, 2009, 42(2): 210-214.

[5]王瑞荣, 郑书万, 陈浩龙, 等. 一种基于Taylor和Kalman的室内协同定位方法[J]. 传感技术学报, 2014, 11(27):1 557-1 561.

[6]丁海强, 齐光快, 庄华亮, 等. 基于负约束条件下最大似然估计的无线传感器网络定位算法[J]. 传感技术学报, 2014, 27(11): 1 545-1 550.

[7]钟丽鸿, 胡成全, 金京姬. 基于RSSI极大似然估计定位算法的分析与实现[J]. 吉林大学学报(理学版), 2014, 52(3): 556-560.

[8] Zhang X F, Liu H Y. Efficient Implementation of Distributed Maximum Likelihood Estimation Method in Clustered Wireless Sensor Networks[J].Sensors &Transducers, 2013, 157(10):101-107.

[9] Simonetto A, Leus G. Distributed Maximum Likelihood Sensor Network Localization[J]. IEEE Transactions on signal processing, 2014,62(6):1 424-1 437.

[10]朱国辉, 冯大政, 向平叶, 等. 传感器误差情况下的线性校正TOA定位算法[J]. 系统工程与电子科技, 2015, 37(3): 498-502.

[11] Li Y, Qian Z, Zhao S,etal.AResearchofTOAwirelesssensornetworklocalizationalgorithm[J].AdvancedMaterialsResearch, 2013, 79 (1):1 601-1 604.

[12]于宁, 万江文, 冯仁剑. 无线传感器网络定位求精方法[J]. 高技术通讯, 2008,18(10):1 017-1 022.

[13]杜巧玲, 钱志鸿, 王树勋. 无线传感器网络二维协作定位方法[J]. 吉林大学学报(信息科学版), 2009, 27(2): 167-172.

[14]SoHC,LinL.Linearleastsquaresapproachforaccuratereceivedsignalstrengthbasedsourcelocalization[J].SignalProcess, 2011, 59(8):4 035-4 040.

[15]LinL,SoHC,ChanFKW,etal.AnewconstrainedweightedleastsquaresalgorithmforTDOA-basedlocalization[J].SignalProcess, 2013,93(11):2872-2878.

(编辑：刘宝江)

A localization algorithm based on Taylor series multivariable expansion model

LIU Cheng-peng, XIA Bin, XIE Nan, PENG Rong-qun

(School of Computer Science and Technology, Shandong University of Technology, Zibo 255049, China)

Abstract:In order to improve positioning accuracy in wireless sensor networks, a new Taylor series multivariable expansion localization model is established by the method of adding the distances information between unknown nodes. In process of the algorithm solution, firstly the maximum likelihood estimation is utilized to obtain initial values of unknown nodes. Then, its optimal values are calculated as the estimated location of unknown nodes by the weighted least squares method. To evaluate the performance of this algorithm, simulations test the impact of different distance measurement error and the number of known nodes on positioning error, and the cumulative distribution function of algorithm. Simulation results show that the proposed algorithm has achieved better performance on positioning accuracy and efficiency.

Key words:Taylor series multivariable expansion; localization model; maximum likelihood estimation; wireless sensor networks

中图分类号：TP393

文献标志码：A

文章编号：1672-6197(2016)03-0061-05

作者简介：刘承鹏，男， liuchengpeng123456@163.com； 通信作者： 夏斌，男， xiabin@sdut.edu.cn.

基金项目：山东省高校科技计划项目(J11LG24)

收稿日期：2015-05-10