Copula函数的选择及股票市场的相关性研究

闫中义， 李新民

(青岛大学 数学科学学院， 山东 青岛 266071)



Copula函数的选择及股票市场的相关性研究

闫中义， 李新民

(青岛大学 数学科学学院， 山东 青岛 266071)

摘要：Copula函数能够完整地刻画变量间的相关关系，在股票市场中用Copula函数来描述股票之间的相关性被广泛应用.本文从6种Copula模型入手，对基于参数自助的似然准则检验方法和基于参数自助的拟合优度检验方法进行了对比分析，研究其在模型选择上的准确性，并将其应用到平安银行和交通银行两支股票中，发现与模拟结果相一致.

关键词：股票； Copula函数； 拟合优度检验； 似然准则； 参数自助

在金融市场中，股票的收益率关系日趋复杂，其相关性研究是研究金融市场关联性的重要内容.利用Copula函数作为工具对股票进行相关性分析有其特有的优势，因为Copula函数能够将边缘分布与联合分布分开来研究，并且在随机变量作单调变换后保持变量间的相关性不变.Bouye[1]，Durrleman和Nikeghbali[2]等人系统地介绍了Copula在金融市场中的一些应用.

Copula是一个函数，它主要用来描述随机变量之间的相关性.Sklar[3]于1959 年首次提出 Sklar 定理并建立Copula函数理论.根据Sklar定理，利用Copula理论建立模型的关键有两步：首先要确定好边缘分布；其次找一个能很好地描述边缘分布的相关结构的Copula函数.目前Copula函数在实际应用中的一个主要问题是函数形式的选择.Embrechts[4]对不同的Copula函数模型进行了比较研究，发现采用不同形式的Copula模型可能导致不同的分析结果. 因此在描述股票间的相互关系时选择合理的Copula函数模型尤为重要.

目前主要根据以下几种思路来选择合理的Copula函数：(1)从金融市场相关性角度出发，通过分析常用Copula函数的特点来进行选择；(2)根据各种信息准则，从给定的集合中选取较为合适的Copula；(3)通过Copula的拟合优度检验选择最优的Copula来描述变量间的相关模式[5]；(4)利用似然函数准则,提出的基于参数bootstrap的模型选择方法[6].

对于上述方法，已有文献对前2种方法进行了对比分析，但尚未见到对后2种方法的对比分析.本文通过对比基于参数自助的似然准则检验和基于参数自助的拟合优度检验两种Copula函数的选择方法进行分析和模拟研究，选出最优的Copula来描述它们之间的相关关系.平安银行(000001.SZ)和交通银行(601328.SS)的股票收益率具有较强的相关性，本文选择这两种股票的Copula函数对这两种股票从2014年4月4日到2015年5月29日共301对交易日的原始数据进行分析研究，从而使购买者能够根据其关联性，优化投资决策，也希望为相关部门提高股票市场的运行效率及监管提供重要的现实参考依据.

1Copula理论

根据Sklar定理，设随机变量(X1,X2)的联合分布函数为

F(x1,x2)=C(F1(x1),F2(x2))

F1(x1),F2(x2)是(0,1)上的均匀分布函数.这样是为了避免计算上的复杂，因为其它的边缘分布的选择在本质上不会改变结论.

联合对数似然函数的具体形式为

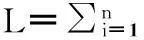
式中c为Copula函数的密度函数，ui,vi,i=1,…,n为样本值.最佳的Copula就是能使联合对数似然函数达到最大时所对应的Copula.

Kendall’s tau 是随机变量关于Copula的一个非参度量.它表示两个相互独立的向量的同向对和异向对概率做差，即如果(X1,Y1)和(X2,Y2)是独立同分布的随机向量，那有

Pr[(X1-X2)(Y1-Y2)<0]

Kendall’s tau同样可以表示成Copula函数的形式

随机变量u，v在(0,1)上均匀分布，C是它的连接分布函数.对于阿基米德Copula，Kendall’s tau 能够写成

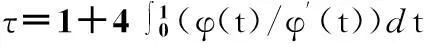
2基于参数自助的似然准则检验方法

参数自助的方法[7]是当样本总体的分布函数形式已知时，可以通过极大似然或Kendall’s tau 等方法来得到参数的估计值，然后重复抽样.基于参数自助的似然准则检验方法的基本做法是利用已知的Copula产生随机样本，即“原始数据”，然后用待选的Copula去拟合，并重复抽样，计算每次的最大似然函数值.最后，利用原始数据的似然值与拟合的似然平均值构造检验统计量.那么能够提供最接近样本值的似然函数值所对应的Copula函数就是所要找的最佳Copula函数.具体做法如下：

(1)选定一个Copula函数，产生n组随机数，构成原始数据(U1,U2,…,Un).

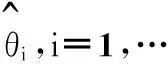
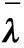
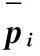
3基于参数自助的拟合优度检验方法

Copula的拟合优度检验[9]的执行都是基于经验Copula的过程：

(1)

Cn是经验Copula

(2)

Cθn是在假设H0:C∈{Cθ}成立的条件下C的一个估计.式(1)中的θn是θ基于秩的估计.检验统计量为

Sn=∫[0,1]dn(u)2dCn(u)=

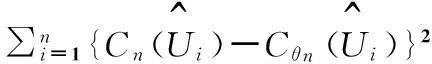
(3)

基于参数自助的拟合优度检验的近似p值可以用如下过程得到：

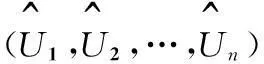
(3)用每一个Copula模型去计算式(3)中检验统计量Snj,j=1,…,m.

(4)重复如下步骤，对每个k∈{1,…,B},

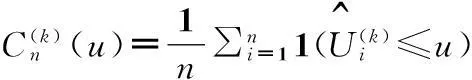
(c)计算Snj,j=1,…,m的一个渐近独立实现：

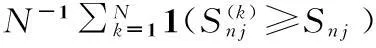
4模拟比较

下面选取6种常用的Copula模型(见表1)，用R软件进行模拟实验来比较这两种方法的检验能力.

表1不同Copula模型的τ和θ

Copula类型C(u,v)τθGumbelexp{-[(-lnu)1/θ+(-lnv)1/θ]θ}1-θ[1,?)Frank-1θlog{1+(e-θu-1)(e-θv-1)e-θ-1}1-4θ+4D1θ()θ-?,?()/0{}Clayton(u-θ+v-θ-1)-1/θθθ+2[0,?)NormalΦθ(Φ-1(u),Φ-1(v);ρ)2πarcsinθ[-1,1]Plackett[1+(θ-1)(u+v)]2(θ-1)-[1+(θ-1)(u+v)]2-4uvθ(θ-1)2(θ-1)无具体表达式(0,+?)/{1}tT2(T-1ν(u1),T-1ν(u2);ρ,ν)2πarcsinθ(-1,1)

对原始数据的样本值，考虑4种秩相关系数，τ=0.2，τ=0.4，τ=0.6，τ=0.8，重复B=1 000次，产生样本容量为n=300的模拟数据.为了简单起见，把Gumbel，Frank，Clayton，Normal，Plackett，t(v=4)简写为G，F，C，N，P，t.原假设为“当数据来自其它的Copula函数时，待检验的Copula函数能够拟合这些数据”.当p值≥0.05时，说明接受原假设，即所对应的Copula函数就是我们所要找的Copula.

从表2中可以得出，对于检验水平为0.05，当相关系数非常小即0.2时，两种方法都无法识别出原始数据所来源的Copula，但当相关系数为0.6，0.8的时候，基于参数自助的似然准则检验方法的优势就显现出来了，除了Normal在0.6的时候没识别出来外，其他Copula均能准确识别.而基于参数自助的拟合优度检验方法在这种情况下只能识别出Clayton来，其他Copula都无法准确识别.

表2不同Copula函数结构下两种方法的平均p值

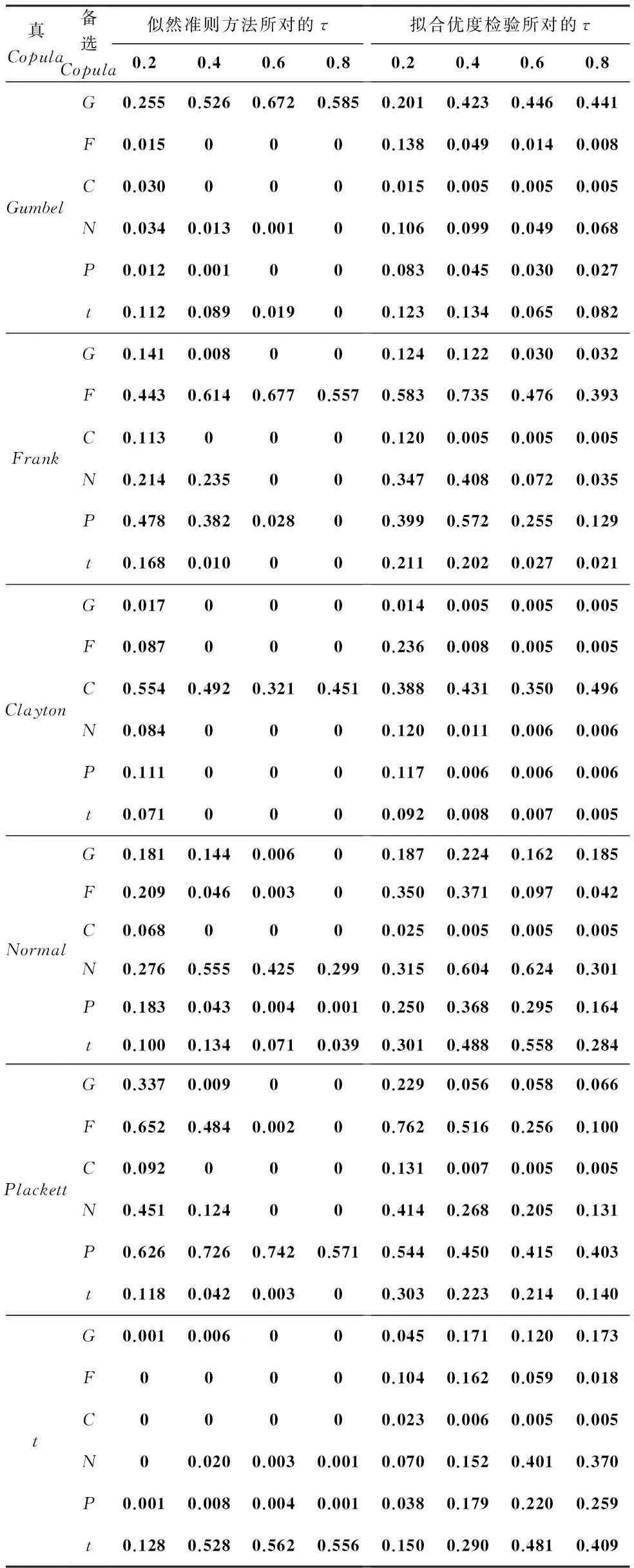
真Copula备选Copula似然准则方法所对的τ拟合优度检验所对的τ0.20.40.60.80.20.40.60.8GumbelG0.2550.5260.6720.5850.2010.4230.4460.441F0.0150000.1380.0490.0140.008C0.0300000.0150.0050.0050.005N0.0340.0130.00100.1060.0990.0490.068P0.0120.001000.0830.0450.0300.027t0.1120.0890.01900.1230.1340.0650.082FrankG0.1410.008000.1240.1220.0300.032F0.4430.6140.6770.5570.5830.7350.4760.393C0.1130000.1200.0050.0050.005N0.2140.235000.3470.4080.0720.035P0.4780.3820.02800.3990.5720.2550.129t0.1680.010000.2110.2020.0270.021ClaytonG0.0170000.0140.0050.0050.005F0.0870000.2360.0080.0050.005C0.5540.4920.3210.4510.3880.4310.3500.496N0.0840000.1200.0110.0060.006P0.1110000.1170.0060.0060.006t0.0710000.0920.0080.0070.005NormalG0.1810.1440.00600.1870.2240.1620.185F0.2090.0460.00300.3500.3710.0970.042C0.0680000.0250.0050.0050.005N0.2760.5550.4250.2990.3150.6040.6240.301P0.1830.0430.0040.0010.2500.3680.2950.164t0.1000.1340.0710.0390.3010.4880.5580.284PlackettG0.3370.009000.2290.0560.0580.066F0.6520.4840.00200.7620.5160.2560.100C0.0920000.1310.0070.0050.005N0.4510.124000.4140.2680.2050.131P0.6260.7260.7420.5710.5440.4500.4150.403t0.1180.0420.00300.3030.2230.2140.140tG0.0010.006000.0450.1710.1200.173F00000.1040.1620.0590.018C00000.0230.0060.0050.005N00.0200.0030.0010.0700.1520.4010.370P0.0010.0080.0040.0010.0380.1790.2200.259t0.1280.5280.5620.5560.1500.2900.4810.409

5实例论证

选取了平安银行(000001.SZ)和交通银行(601328.SS)从2014年4月4日到2015年5月29日，共301对交易日的原始数据(见图1)，对这301对交易日的收盘数据取对数收益率，然后利用经验分布得到300对在(0,1)上的数据，构成我们的数据(见图2).利用G，F，C，N，P，t6种Copula来拟合,经计算，这两只股票对数收益率的相关系数τ=0.59，整体上具有较强的相关性.

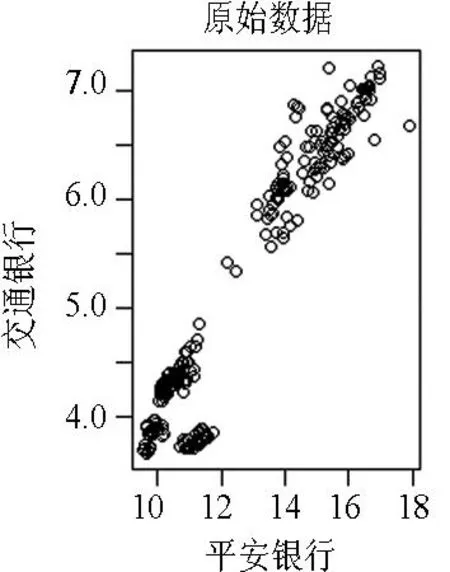
图1301对交易日的收盘数据

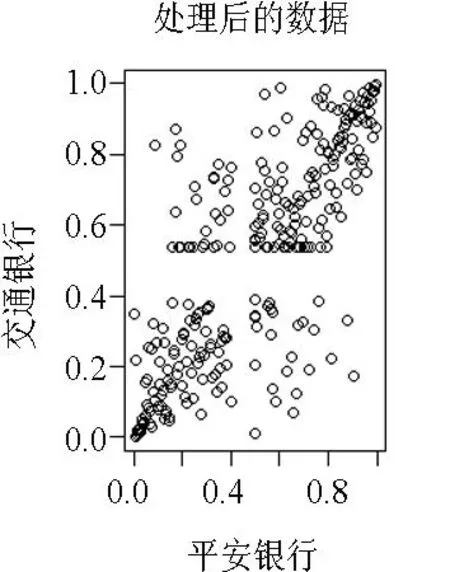
图2300对(0，1)上的数据

设Ct表示第t日的收盘价，并令πt表示相应的日对数收益率，有

πt=100(lnCt-lnCt-1)

表3两种方法的平均p值

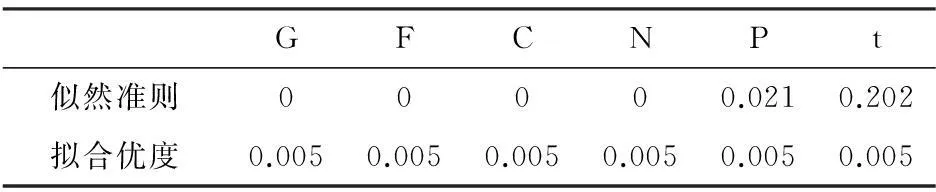
GFCNPt似然准则00000.0210.202拟合优度0.0050.0050.0050.0050.0050.005

从表3可以看出，基于参数自助的似然准则检验方法表明平安银行和交通银行这两支股票的关系用自由度为4的tCopula来描述非常合适.而基于参数自助拟合优度检验的方法无法识别.又由表2的模拟和分析结果可知，当相关系数为0.6时，基于参数自助的似然准则检验方法能够很好识别除Normal外的其他Copula；而基于参数自助的拟合优度检验方法在这种情况下只能识别出Clayton来，其他Copula都无法准确识别.因此，平安银行和交通银行这两支股票的对数收益率可用自由度为4的tCopula来描述.

所以当两支股票相关性较强时，对Copula函数的选择用基于参数自助的似然准则检验方法比较好.

6结束语

本文通过模拟比较和实例论证，对比了基于参数自助的似然准则检验方法和基于参数自助的拟合优度检验方法，发现基于参数自助的似然准则检验方法在数据之间相关性较强的情形下，检验结果很稳定并且识别率高，这样我们就可以根据一支股票的走势而推断出另一支股票的走势来，是一个非常好的Copula模型的选择方法.用这个方法做参考，股票投资者就可以合理地搭配自己所购买的股种，进行优化投资.

参考文献：

[1]BouyéE,DurrlemanV,NikeghbaliA,etal.Copulasforfinance:Areadingguideandsomeapplications[J].SsrnElectronicJournal, 2000.

[2]DurrlemanV,NikeghbaliA,RoncalliT.Whichcopulaistherightone?[J].SsrnElectronicJournal, 2000.

[3]SklarM.Fonctionsderépartitionàndimensionsetleursmarges[J].Publ.inst.statist.univ.paris, 1959, 8(1):229-231.

[4]EmbrechtsP,LindskogF,McneilEJ.Modellingdependencewithcopulasandapplicationstoriskmanagement[J].HandbookofHeavyTailedDistributionsinFinance, 2003,1(8):329-384.

[5]FermanianJD.Goodness-of-fittestsforcopulas[J].JournalofMultivariateAnalysis, 2005, 95(1):119-152.

[6]NikoloulopoulosAK,KarlisD.Copulamodelevaluationbasedonparametricbootstrap[J].ComputationalStatistics&DataAnalysis, 2008, 52(7):3 342-3 353.

[7] 吴建华, 王新军, 张颖. 相关性分析中Copula函数的选择[J]. 统计研究, 2014 , 31(10):99-107.

[8]MardiaK,KentJ,BibbyJ.Multivariateanalysis[M].London:AcademicPress, 1979.

[9]KojadinovicI,YanJ.ModelingmultivariatedistributionswithcontinuousmarginsusingthecopulaRpackage[J].JournalofStatisticalSoftware, 2010, 34(9):1 346-1 352.

(编辑：郝秀清)

The selection of Copula model and the correlation analysis in stock market

YAN Zhong-yi, LI Xin-min

(College of Mathematics, Qingdao University, Qingdao 266071, China)

Abstract:The copula function could describe the correlation between several variables, so the model selection of copulas is particularly important. In this article, we select six kinds of copulas. The method of likelihood criterion based on parametric bootstrap and the method of goodness-of-fit test based on parametric bootstrap are used to compare the accuracy of model selection. We also use the two methods to test the relationship of PingAn stock and JiaoTong stock, and find that the result is same as results of simulation.

Key words:stock; Copula; goodness of fit tests; likelihood criterion; parametric bootstrap

中图分类号：O212

文献标志码：A

文章编号：1672-6197(2016)03-0042-04

作者简介：闫中义，女，447468203@qq.com; 通信作者：李新民，男，xmli@qdu.edu.cn

基金项目：山东省自然科学基金项目(ZR2014AM019)

收稿日期：2015-07-07