基于自适应多目标指数罚函数的NSGA-II算法

王　聪， 赵文玲

(山东理工大学 理学院， 山东 淄博 255049)



基于自适应多目标指数罚函数的NSGA-II算法

王聪， 赵文玲

(山东理工大学 理学院， 山东 淄博 255049)

摘要：为求解多目标优化问题，将快速非支配进化算法(NSGA-II)进行了推广，构造了一种新的多目标指数罚函数，将其作为NSGA-II算法的适应度函数，通过每次自适应更新罚因子，以此获得多目标规划问题的有效解(Pareto解).仿真结果表明，该算法在快速收敛的情况下，能够获得更加均匀的Pareto前沿.

关键词：多目标规划； 罚函数； NSGA-II算法； 自适应罚因子； 约束优化

工程中的很多问题被描述为数学优化问题，可以根据目标函数的数目将其分为单目标优化问题和多目标优化问题.但在实际中，很多问题都被描述为带有复杂约束的多目标规划问题，因此研究求解此类问题的算法具有重要的意义.

目前处理带有复杂约束的多目标规划，主要用到罚函数方法与NSGA-II算法结合[1-2]以及一些改进的NSGA-II算法[3-5].罚函数法是处理带有约束的优化问题常用的方法之一，其中包括序列无约束极小化技术法(SUMT)，增广拉格朗日罚函数法，精确罚函数法等[6].由于这些算法所构造的罚函数以及罚因子的选取不当，很大程度上降低了NSGA-II算法效率，使得罚函数法在处理带有约束的多目标规划问题时略显无力.而对于改进NSGA-II算法，虽然避开了罚因子的选取问题，但是由于需要引进了辅助算子，在一定程度上丢失了NSGA-II算法的原有的优点.

鉴于以上缺陷，本文提出了一种自适应多目标指数罚函数的NSGA-II算法，构造新的指数罚函数，将该指数罚函数作为NSGA-II算法的适应度函数，在迭代过程中结合NSGA-II算法的特点，自适应更新罚因子，将带有约束的多目标规划模型转化为无约束多目标指数罚函数模型.这种算法不仅成功地解决了罚因子的选取问题，而且最大程度的保留了NSGA-II算法原有的优点，增加了该算法的适用性.

1一种新的多目标指数罚函数模型

对于单目标规划问题(P):

(1)

其中，目标函数和约束函数都是连续可微.1994年，R.Cominetti等人提出了指数罚函数[7]，形式如下:

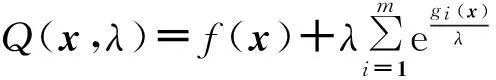
(2)

其中，λ>0.并且指出，这一类罚函数是简单光滑，但不是精确的.

最近，张连生等[8]在文献中对单目标规划提出一种新的指数罚函数:

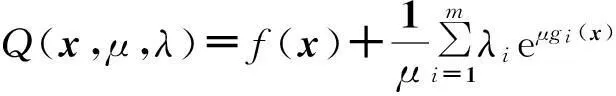
(3)

其中，μ>0，λi≥0，这种指数罚函数是简单的、光滑的、精确的.

本文将这种思路引入到多目标规划中，构造新的多目标指数罚函数.

考虑多目标规划问题(VP):

(4)

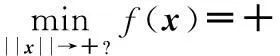
对(VP)构造了一种新的指数罚函数，将其转化为无约束优化问题(VP1):

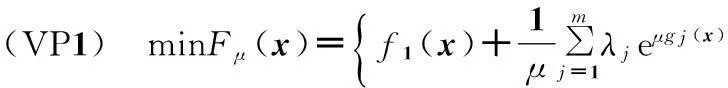
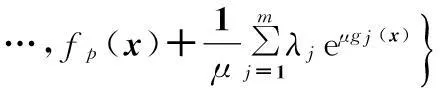
(5)

其中，μ>0是罚因子. 将该模型作为NSGA-II算法的适应度函数，结合NSGA-II算法的特点对罚因子进行自适应更新，进行求解.

2NSGA-II算法

考虑如下只带有线性约束的多目标规划模型(LVP)

minF(x)={f1(x),f2(x),…,fp(x)}

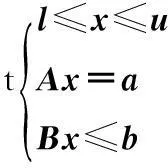
其中，x,l,u为n维向量，a为m维向量，b为p维向量，A为m×n维矩阵，B为p×n维矩阵.

NSGA-II是求解(LVP)常用的进化算法，该算法主要包括非支配排序算子，拥挤度算子，选择算子，精英保留算子[9].

快速非支配排序算子根据偏序的定义，初步判断种群中个体的优劣程度.

算法步骤:

Step1初始化集合Sp，用来保存被p所支配的个体，初始化np=0，用来记录被p所支配个体的数目；

Step2对于每个在种群中个体q，若个体p支配个体q，则将q包含在Sp中，若q支配p，则np=np+1；

Step3若np=0，则表示没有个体可以支配p,将p放入第一前端F1，并且令p的序值为1，若遍历完种群的每个个体，则进行Step2，否则，返回Step1，继续寻找序值为1的个体，并且更新集合F1.

在对整个种群进行完遍历后，可以得到第一前端F1，然后在集合Sp中寻找剩余的前端.

算法步骤:

Step1初始化前端计数i=1.

Step2初始化集合Q为空集，将其作为第i+1个前端中个体的存储集合.

Step3遍历Fi中的个体p，对于在Sp中的每个个体q，nq=nq-1，若nq=0，则表示在子集中，没有个体可以支配q，令q的序值为i+1，将q放入集合Q.

Step4令i=i+1，Fi=Q，并且返回Step2.

通过以上操作，可以确定种群中每个个体的序值，和每个个体支配的集合，以及支配个体的数目.

拥挤距离算子是计算种群中属于同一序值的每个个体之间的欧式距离，只有在序值相同时，才有距离比较的意义.首先，将位于某前端两个端点的个体的拥挤距离设为无穷大，对于不是端点的个体，计算方法是求得该个体和前后两个目标函数值大小接近的个体的目标函数值之差.

选择算子采用锦标赛选择算法，对于种群中的每个个体，有两个属性可以判断其优劣程度.在整个种群中，首先根据序值选择出序值小的个体，对于属于同一序值的个体，选择拥挤距离大的个体，这样既能使得种群中优秀的个体保存下来，又能增加种群的多样性.

将各个算子结合到一起，得到NSGA-II算法.

算法步骤:

Step1初始化种群，设定种群数目，变异参数，交叉参数，初始迭代代数i=0，最大代数G.

Step2计算个体的序值，拥挤距离，进行选择操作.

Step3对选择出来的子种群进行交叉和变异操作，将子种群与父代种群合并.

Step4对合并后的种群进行裁剪操作，产生与初始种群数目相同的新种群，并且，令i=i+1:若i等于G，则终止迭代，输出结果，否则，转Step2.

3自适应算法步骤及数值仿真

现有算法的普通罚因子更新策略为

μk=Kk+μk-1

(6)

其中K为大于0的常数，k是迭代次数，在初始化时，很难选择合适的K，若K选择过小，会影响罚因子的增加速度，若K选择过大，会使得迭代末期整个种群中可行解个体的比例降低，所以通常采取试探的方法，寻找合适的K，这样大大降低了算法的运行效率，增加了运行时间.

下面提出一种新的自适应罚因子更新策略:

μk=μk-1(1+eρ+1)

(7)

其中ρ表示在前一次迭代后，整个种群中，可行解个体所占的比例.因此，0≤ρ≤1，并且随着迭代的进行，种群中可行解比例越来越高，即ρ趋近于1.在算法运行初期，由于可行解比例比较小，罚因子较大，因此可以搜索尽可能多的可行解，在算法后期，罚因子减小，因此可以在可行解中搜索尽可能多的最优解，由于引进了自适应搜索，使得当种群中可行解比例趋近于1时，罚因子更快速趋近于0，提升了算法效率，成功地解决了K的选取问题.

下面给出本文的算法.

基于自适应多目标指数罚函数的NSGA-Ⅱ算法步骤:

Step1给定罚函数参数向量μ0，λ0，终止条件ε，以及初始次数k=1.

Step2构造多目标指数罚函数序列:

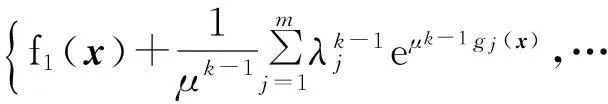
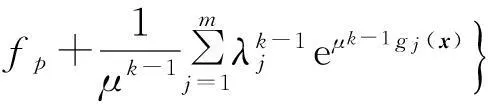
将其作为适应度函数，用NSGA-II算法求解该模型，计算每一次迭代后种群中可行解比例ρ，若‖Xk-Xk-1‖≤ε，则输出结果，否则转Step3.

下面应用此算法求解算例1、算例2.

算例1

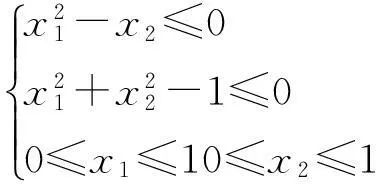
表1可行解比例与罚参数关系

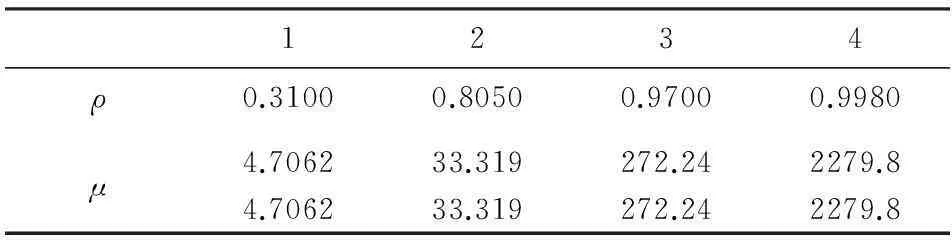
1234ρ0.31000.80500.97000.9980μ4.706233.319272.242279.84.706233.319272.242279.8

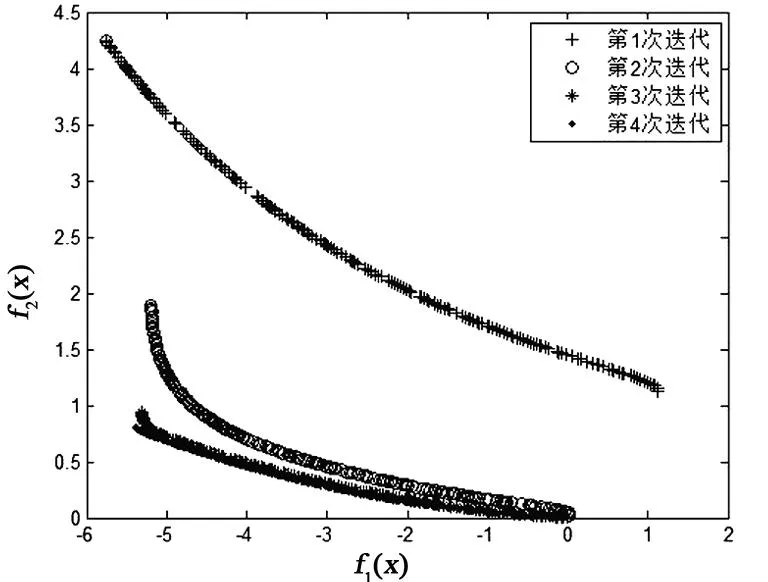
图1　例1迭代过程与Pareto解

下面对算例1利用普通罚因子更新策略式(6)进行数值仿真，并与自适应罚因子更新策略式(7)进行比较.在式(6)中分别选择当K=1,10,40,100,得到表2.

表2普通罚因子与自适应罚因子比较

K=1K=10K=40K=100自适应迭代次数147534运行时间/s4922.912.99.8711.9可行解比例0.9900.9930.9890.9550.998

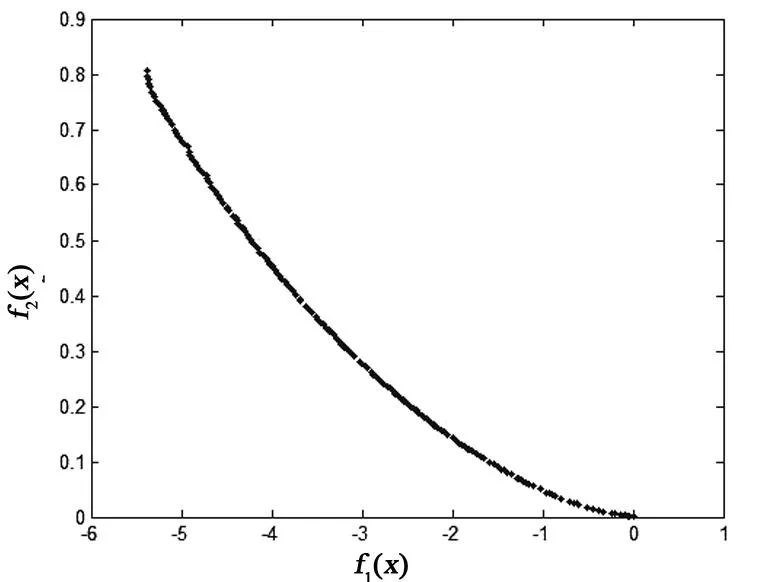
图2　例1最终迭代与Pareto解

由表2可以看出，若初始值K选择过小，则增加了算法的迭代次数和程序运行时间；若K选择过大，虽然迭代次数减少了，但是在最后的Pareto解中，可行解比例明显下降.从表2中可以看出自适应更新策略不仅在迭代次数和运行时间，以及最终可行解比例方面，都优于非自适应罚因子.

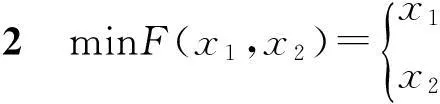
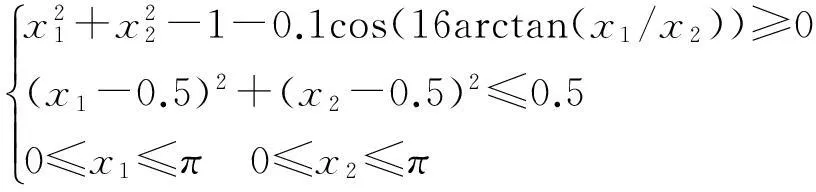
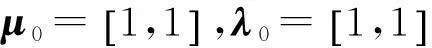
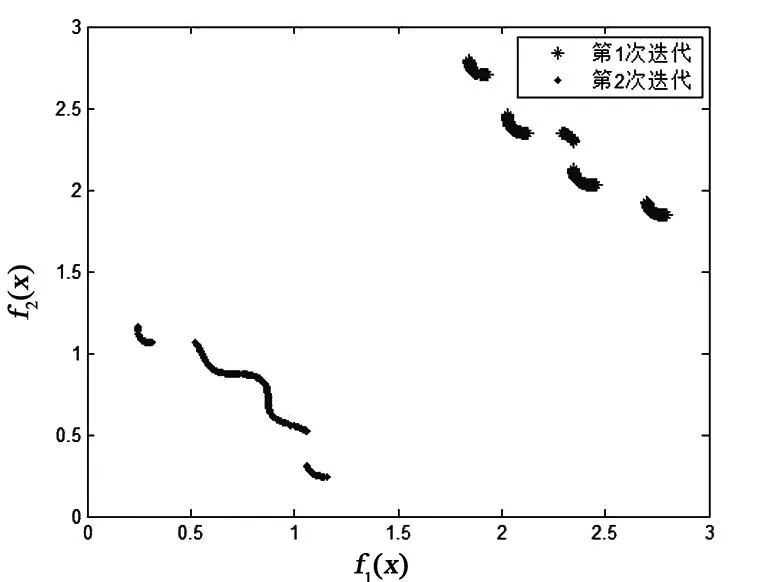
图3　例2迭代过程与Pareto解

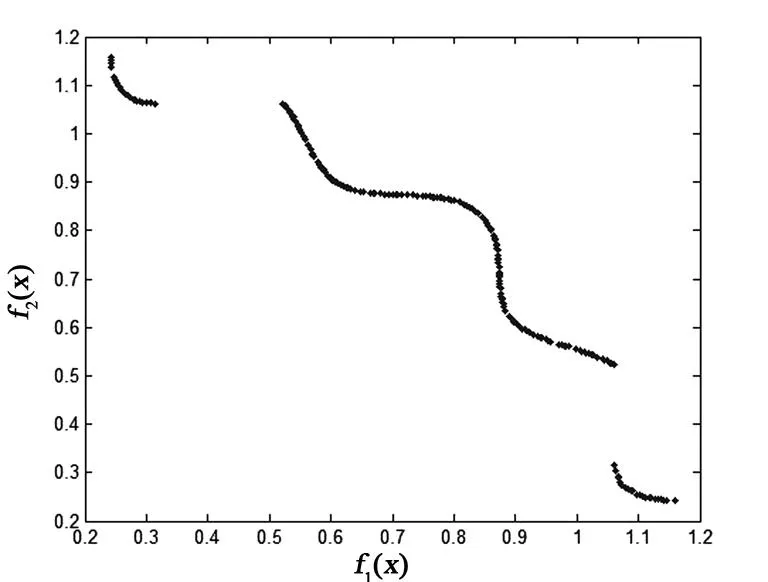
图4　例2最终迭代与Pareto解

本文提出的多目标指数罚函数，将其作为NSGA-II的适应度函数，并且结合多目标遗传算法的特点，对罚因子进行了自适应更新，避免了因为罚因子选取不当造成的麻烦.最后通过数值仿真，可以看出本文的算法不仅迭代次数少，而且可以得到更优的Pareto前沿.本文提出的算法将NSGA-II算法推广到了带有非线性约束的多目标规划领域，扩大了该算法的适用范围.

参考文献：

[1]刘涛, 苏成利, 李平. 基于外点惩罚函数与NSGA-II算法的气体分馏装置多目标优化[J]. 江南大学学报(自然科学版), 2014, 12(6):658-665.

[2]邹宏涛. 网格独立任务的新型多目标安全模型及遗传算法求解[D]. 西安: 西安电子科技大学, 2012.

[3]黄冀卓， 王湛， 马人乐. 一种新的求解约束多目标优化问题的遗传算法[J]. 计算机工程与应用， 2006， 42(23): 47-51.

[4]陈志旺， 陈林. 求解约束多目标区间优化问题的改进NSGA-Ⅱ[J].小型微型计算机系统， 2014，35(11):2 502-2 506.

[5]王珑, 王同光, 罗源. 改进的NSGA-II算法研究风力机叶片多目标优化[J]. 应用数学和力学, 2011, 32(6):693-701.

[6]李政. 非线性规划中的两种罚函数[D]. 上海：上海大学， 2007.

[7]CominettiR，DussaultJP.Stableexponential-penaltyalgorithmwithsuperlinearconvergence[J].JournalofOptimizationTheory&Applications， 1994， 83(2):285-309.

[8]张连生，顾燕红. 简单光滑精确指数乘子罚函数[J]. 数学年刊(中文版), 2010， 31(4):475-486.

[9]KöppenM,YoshidaK.Substitutedistanceassignmentsinnsga-IIforhandlingmany-objectiveoptimizationproblems[C]//ShigeruO,KalyanmoyD,CarloP,etal.EvolutionaryMulti-CriterionOptimization.Germany:SpringerBerlinHeidelberg, 2007:727-741

(编辑：刘宝江)

NSGA -II based on adaptive multi-objective exponential penalty function

WANG Cong, ZHAO Wen-ling

(School of Science, Shandong University of Technology, Zibo 255049, China)

Abstract:In order to solve multi-objective programming problem，this paper extended the NSGA-II algorithm，and constructed a new multi-objective exponential of penalty function as the fitness function of NSGA-II algorithm.It could to obtain the Pareto solutions of multi-objective programming problem through dynamic updating penalty factor. Finally，the simulation results showed that the algorithm not only converged fastly，but also obtained more uniform Pareto frontier.

Key words:multi-objective programming problem； penalty method； NSGA-II； adaptive penalty factor； constrained optimization

中图分类号：O224

文献标志码：A

文章编号：1672-6197(2016)03-0011-04

作者简介：王聪, 男, 596520206@qq.com; 通信作者：赵文玲, 女, zwlsdj@163.com

基金项目：国家自然科学基金项目(11271233); 山东省自然科学基金项目(ZR2012AM016)

收稿日期：2015-09-10