网络点边对偶性变换及其性质研究

曲超　袁瑞芬　张国炼

(东莞理工学院　计算机学院，广东东莞　523808)



网络点边对偶性变换及其性质研究

曲超袁瑞芬张国炼

(东莞理工学院计算机学院，广东东莞523808)

摘要：针对网络拓扑变换提出了一种新的点边对偶性变换方式，即将原始网络中的边映射为结点，结点映射为邻接边之间的多个二元关系。提出并证明了该变换的某些特性。通过实验对相应性质在不同结构网络中的表现加以验证。

关键词：网络拓扑；点边对偶变换；复杂网络；网络性质

目前，互联网规模越来越大，结点间相互作用复杂，其拓扑结构基本上未知或未曾探索[1]。人们对描述真实系统拓扑结构的研究经历了从欧几里德格网到随机图，再到直到最近几年发现的复杂网络模型。小世界网络和无标度网络的发现，掀起了复杂网络的研究热潮，同时也带动了各种网络拓扑应用的蓬勃发展。其中对于网络拓扑模型变换的研究主要应用于交通网络。其主要方法是将交通网络抽象为复杂网络的形式，这些复杂网络是对交通网络的映射，不同的抽象方法所获得的复杂网络图，能够从不同的角度反映出交通网络的特点。其中主要包括：L-space、 C-space[2]、B-space[3]、P-space[4]、Primal Approach[5]以及Dual Approach[6]等。

上述的各类方法都是以逻辑概念做为变换依据，例如Dual Approach方法，将若干个连续的同名道路视为一个结点，将道路的交叉路口映射为结点间边，虽然能够对交通网络加以描述，但未能将网络信息与道路实体相联系，导致在实际应用中产生各种问题。

1复杂网络的基本概念

复杂网络的复杂性体现在两个方面：其一，复杂网络常常包含海量的结点，即结点数量非常庞大；其二，复杂网络之间的连接关系通常较为复杂。其主要度量参数及含义如下。

1)度分布。结点vi的度ki被定义为与该结点连接的相邻结点的数目，所有结点的度的平均值称为网络的平均度，记为。网络中结点的度分布用度分布函数P(k)来表示，含义是任意一个结点有k条边的概率，也等于网络中度为k的结点的数目占结点总数的比例。复杂网络研究的另外一个重大发现是大部分大规模真实网络在中，两种度分布较为常见：一是指数度分布,即P(k)随着k的增大以指数形式衰减；另一种分布是幂律分布，即P(k)~k(-γ)，其中γ称为度指数，不同的网络，其动力学性质也不同。另外,度分布还有其它形式，如星型网络的度分布是两点分布，规则网络的度分布为单点分布。

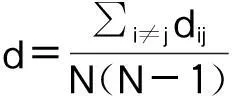
4)介数。介数通常分为边介数和结点介数两种。结点介数定义为网络中所有最短路径中经过该结点的路径的数目占最短路径总数的比例。边介数定义为网络中所有最短路径中经过该边的路径的数目占最短路径总数的比例。介数反映了相应的结点或者边在整个网络中的作用和影响力，是一个重要的全局几何量，具有很强的现实意义。根据结点和边得介数,能够分析网络系统中任意一个结点和另外结点之间的关联，这种关联被删除或是失效时对整个系统的影响。

5)度和簇系数之间的相关性。网络中度和簇系数之间的相关性被用来描述不同网络结构之间的差异，包括连接度不同的结点的相关性和结点的度与其簇系数之间的相关性。在网络系统中，度和簇系数之间的相关性有助于分析系统的层次性和模块程度。

用上述参数可以很方便地衡量现实网络的特性。根据Newman的观点[8]，现实网络大致分为四种：社会网络、信息网络、技术网络和生物网络。这四种网络虽然各自具有不同的物理形式、彼此描述的系统各异、其结点和边的定义差别也很大，但它们却具有一些相同的特征：网络结点间的作用很复杂，而且高度不规则；结点之间在度、簇系数、集中性等网络特征度量方面表现出不对称性，不同结点差异很大；尽管这些网络大而复杂，结点间的平均距离却很小，呈现出小世界特性。大量的实证研究表明：现实世界中的许多网络具有下面三个共同特性:结点度服从度指数介于[2,3]的幂律分布；集聚程度高；结点间平均距离小。

2网络点边对偶变换

对于交通网络模型，Dual方法将句法空间里同名的多条边看做一个结点，不能全面地反映出的城市道路网络的深层特性。为此提出一种更具普遍意义的点边网络对偶变换。

不同于对偶图，对偶变换图是将原图G中的边转换为结点，G中的结点转换为新图中的边集。同样，不同于Dual Approach方法，点边对偶变换图将任意一条边看作新图中的一个点，而不是在句法空间里将同名的多条边作为新图中的一个点，该定义更具普遍性。由定义可知对偶变换图具有如下性质：

定理1|V′|=|E|，即对偶变换图G′的结点数等于原图G中边的条数。

证明 由定义可知该定理成立。

定理2G中的每一个结点在G′中转化为一个团(clique)，且任意两个团之间没有公共边。

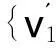
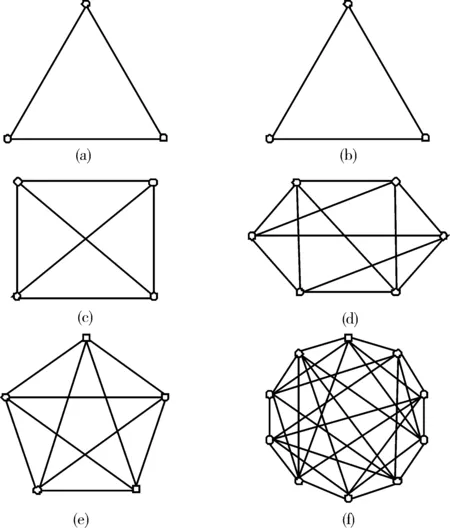
图1　k3，k4，k5及其点边对偶变换图

推论1G中度为n的结点在G′中转化为Kn。

推论2G′中由G中结点转化的团两两之间最多只有一个公共点。

推论3G′中由G中度大于2的结点转化的团都是极大团。

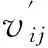
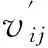
证明由定理2可知，G中度为di的结点vi在G′中转化为团kdi，其度数为di*(di-1)，又任意两个团之间没有公共边，因此图G′的度数和为所有团的度数和。

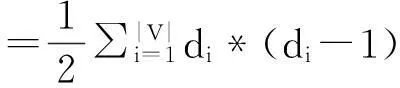
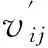
定理5表明在对偶变换后结点的簇系数不再依赖于对与目标结点相邻的结点之间边数的计数，而是可以根据原始网络结点的度来唯一确定。该性质将对交通网络的研究起到较为重要的作用。

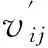
3点边对偶性变换的复杂网络特性测试

对1 000个结点的随机网络[9]、小世界网络[10]以及无标度网络[11]进行点边对偶性变换，并考察其度量参数。

图2　随机网络及其变换图的度分布

图3(a)、(b)分别显示了平均度为4、6、8的小世界网络及其点边转换后的网络的度分布情况。与随机网络相似，小世界网络的度分布呈现正态分布的特性，因而其点边转换图的度分布也表现为正态分布。

图3　小世界网络及其变换图的度分

图4　无标度网络及其变换图的度分布

图4(a)、(b)分别显示了平均度为4、6、8的无标度网络及其点边转换后的网络的度分布情况。由于无标度网络度分布服从幂率分布，而幂率分布不具备线性可加性，因而点边转换后的网络度分布并不符合马太效应。虽然如此，但从图像中可以看出其度分布近似于幂率分布，导致该现象的原因有待进一步研究和探索。

以上网络的簇系数及平均最短路径长度如表1所示。

表1　簇系数及平均最短路径长度

从表1可以看出，随机网络、小世界网络和无标度网络经过转换后簇系数有所增大，其原因在于根据推论1，原始网络的结点在转换后的网络中被转换为若干团，因而导致簇系数有所增大。根据定理6可知平均最短路径长度应随转换有所增大，但其幅度并不会很大，表1也验证了这一点。

4结论

网络点边对偶变换提供了一种新的网络拓扑结构研究方法。对于随机网络、小世界网络该变换基本保持了原图的度分布规律、簇系数和平均最短路径长度；对于无标度网络，其簇系数和平均最短路径长度仍能与原图保持基本一致。所证明的性质及实验所的结论可应用于交通网络系统、生物学研究以及政治、经济、管理等领域。该变换的更多性质有待进一步研究和探索，在信息网络模型中具有重要的研究价值。

参 考 文 献

[1]Albert R, Barabasi A-L. Statistical mechanics of complex networks[J]. Reviews of Modern Physics, 2002, 74(1): 47-97.

[2]Ferber C V, Holovatch T, Holovatch Y, et al. Public transport networks: empirical analysis and modeling [J]. Eur Phys J: B, 2009,68(2): 261-275.

[3]Zhang P P, Chen K, He Y. Model and empirical study on some collaboration networks [J]. Phys: A, 2006,360(2): 599-616.

[4]Ferber C V, Holovatch T, Holovatch Y, et al. Network harness: metropolis public transport [J]. Phys: A, 2007, 380(1):585-591.

[5]Porta S, Crucitti P, Latora V. The network analysis of urban streets: a primal approach [J]. Envir Planning: B, 2006,33: 705-725.

[6]Porta S, Crucitti P, Latora V. The network analysis of urban street: a dual approach [J]. Phys: A, 2006, 369(2): 853-866.

[7]Watts D J, Strogatz S H. Collective dynamics of ‘small-world’ networks[J]. Nature, 1998, 393:440-442.

[8]Newman M E J. The structure and function of complex networks[J]. SIAM Review, 2003, 45(2):167-256.

[9]Vanhoucke M, Demeulemeester E, Herroelen W. A New Random Network Generator for Activity-on-the-Node Networks[J]. Journal of Scheduling, 2000, 6(1):1-23.

[10]Porter M A. Small-world network[J]. Scholarpedia, 2012, 7(2):1739.

[11]Cesar A H R, Barabási A L. Scale-free networks[J]. Encyclopedia of Genetics Genomics Proteomics & Informatics, 2008, 3(5):1716.

Vertex-Edge Duality Transformation for Network and Its Properties

QU ChaoYUAN RuifenZHANG Guodong

(Computer College, Dongguan University of Technology, Dongguan 523808, China)

AbstractThe paper proposes a new vertex-edge duality transformation method, that is, the edge mapping as a node, and the node mapping as a two element relationship between the adjacent edges, proving some properties about the duality transformation, and verifying the performance of the corresponding properties in different structures by experiments.

Key wordsnetwork topology; vertex-edge duality transformation; complex network; network properties

文章编号：1009-0312(2016)01-0001-06

中图分类号：TP301

文献标识码：A

作者简介：曲超(1979—)，男，山东烟台人，讲师，主要从事数据挖掘、语义网和物联网等方面研究。

基金项目：东莞理工学院2014年大学生创新创业训练计划项目(201411819023)。

收稿日期：2015-07-08