与联盟值有关的联盟结构生成优化

李少芳

(莆田学院　信息工程学院，福建莆田　351100)



与联盟值有关的联盟结构生成优化

李少芳

(莆田学院信息工程学院，福建莆田351100)

摘要：基于势结构与联盟值无关的联盟结构生成算法的研究成果,可以应用到与联盟值有关的联盟结构生成优化中。同时，在与联盟值有关的问题研究中，充分利用给定的联盟值信息进一步优化计算，提高效率。文中介绍了同势的联盟值信息提取方法，并给出应用实例，减少的搜索空间接近一半。

关键词：多Agent；联盟结构；势结构；算法优化；联盟值

联盟结构生成问题已经被证明是NP-完全的。对于n个Agent产生的搜寻空间以O(nn)和 ω(nn/2)指数增长[1-3]，通过遍历所有联盟结构来找到一个最优联盟结构是行不通的。通常在有限时间内只能有选择地搜索部分联盟结构，得到一个满足给定限界k的次优联盟结构。

与联盟值无关的联盟结构生成算法，以不同搜索单位、不同搜索路径加以区分，取得很大进展。Sandholm等的算法[1]采用对联盟结构图首先搜索L1、L2、Ln层(它们只占联盟结构图的极小部分)，可得到收益不低于最优收益1/[n/2]的联盟结构。然后再执行自上往下逐层搜索方法，任意时间停止，可以得到一个满足一定限界要求的解，但是要得到全局最优解，必须搜索完所有可能的Agent联盟结构。胡山立等的算法[4]在搜索L1、L2、Ln层后，采用隔层搜索的方法，以最少的搜索层改进Sandholm等的算法。Dang等人[5]首次提出不是以层为搜索单位的算法。搜索所有最大联盟的势不大于[n(q-1)/q]的联盟结构，可得到收益不小于最大收益1/(2q-1)的联盟结构。苏射雄等[6-7]明确提出基于更小的搜索粒度势结构的搜索算法。刘惊雷等[8]提出一种快速构建最优联盟结构的DP算法。这些算法也适用于与联盟值有关的问题研究中[9-10]，可以针对任意的Agent联盟收益函数，但是如果要得到最优的联盟结构，这些算法仍需要搜索完所有可能的Agent联盟结构，搜索量非常大。利用已知的联盟值信息，可以更有效地减小搜索空间。张新良等[9]的SCS算法在Agent收益函数满足合作收益独立性的前提下，对具有同构关系的的Agent联盟结构按收益大小排序，通过将收益不是最大的剪枝来减少了搜索量。

1势结构CCS

设n个Agent的集合A={a1, a2, a3, …, an}，A中的一个非空子集C称为Agent的一个联盟。联盟C中Agent的个数称为联盟C的势，记为|C|。A的一个完全的划分称为一个联盟结构CS。最优联盟结构用CS*表示。设联盟结构CS={C1, C2,…, Cp}，不失一般性地，设|C1|≥|C2|≥…≥|Cp|≥1。令n1=|C1|,n2=|C2|,…,np=|Cp|,n=n1+n2+…+np，称{n1,n2,…,np}为联盟结构CS的势结构[5]，记为CCS。整数n的每一种划分对应一种势结构，例如，整数6的一种划分表示为6=2+2+1+1，正好对应势结构{2, 2, 1, 1}。在正整数n的所有不同的划分中，将最大加数n1不大于m的划分个数记做f(n，m)，其值可以通过如下的递归方法计算[11]。n个Agent的势结构数就是整数n的划分数，值等于f(n，n)，时间复杂度为O(n2)。

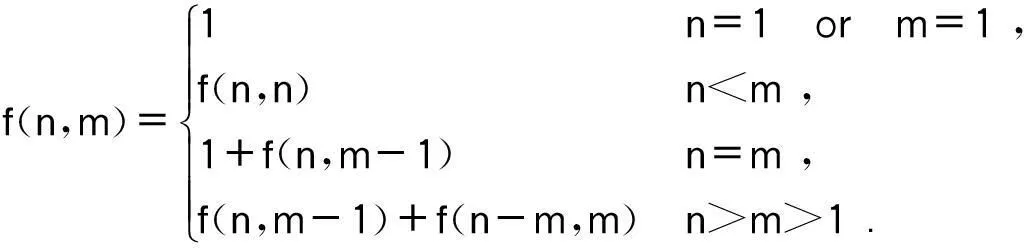
以n=5为例，5个Agent的所有7个势结构分别是{5}、{4, 1}、{3, 2}、{3, 1, 1}、{2, 2, 1}、{2, 1, 1, 1}、{1, 1, 1, 1, 1}，它们对应的联盟结构数分别为1、5、10、10、15、10、1，总共52个。

2同势的联盟值信息提取

可以根据势结构CCS划分联盟结构空间，并尽可能找到包含最优解或次优解的势结构后，再对其所对应的联盟结构进行搜索，减少搜索量，在合理时间内找到最优解或次优解。下面表1给出n=5时的一组联盟值。考察不同势的联盟值，计算各势的联盟上界值和平均值，对低于平均值的联盟进行剪枝。

表1　n=5时各联盟值

算法主要分三步进行：

Step 1：算法要求输入所有联盟C的v(C)值，并给定一个限界k,1/k∈[0.5, 1]，这时可能返回的局部最优解，其质量保证至少是最优解的1/2。可以用联盟的势|C|作为下标，定义两个一维数组max和avg，用以存放势|C|的所有联盟的上界值和平均值。单联盟如{{1},{2}, …,{n}}和全联盟{1, 2, …, n}的值首先作为局部最优解。

Step 2：对应势结构，用保留的联盟构造出联盟结构，搜索找到该势结构对应的最优解或次优解的联盟结构。

Step 3：对比第二个阶段找到的各联盟结构，在合理时间内找到最优解或次优解CS*。

后两个阶段只要找到最优解(k=1)或是足够好的解(也就是0.5< k< 1)，算法停止。

在循环遍历势结构的搜索过程中，不创建任何多余或无效的联盟结构。

3搜寻优化示例

以表1数据为例来说明算法的搜索优化过程如下。5个Agent的所有7个势结构分别是{5}、{4, 1}、{3, 2}、{3, 1, 1}、{2, 2, 1}、{2, 1, 1, 1}、{1, 1, 1, 1, 1}。势为1, 2和5的联盟必须先被搜索， 得到k=2.5的局部最优解。势结构{5}对应的由唯一的全联盟构成的联盟结构{1, 2, 3, 4, 5}的值=250， 势结构{1, 1, 1, 1, 1}对应的由单联盟构成的联盟结构{{1},{2},{3}, {4},{5}}的值=200， 首先比较这两个值， 取较大者250为局部最优解。

势结构{4, 1}中的4对应的联盟， 根据max[4]=220和avg[4]=190， 只从{1, 2, 4, 5}(190)、{1, 3, 4, 5}(220)、{2, 3, 4, 5}(200)中选取。势结构{4, 1}中的1对应的单联盟， 根据max[1]=60和avg[1]=40， 只从{1}(50)、{2}(40)、{5}(60)中选取。因此， 较快找到势结构{1, 4}对应的最优联盟结构{{1,3, 4, 5}, {2}}， 值为260。

势结构{3，2}中的3对应的联盟， 根据max[3]=190， avg[3]=142， 只从{1，2，3}(160)、{1, 4, 5}(150)、{2, 3, 4}(150)、{2, 4, 5}(180)、{3, 4, 5}(190)中选取。势结构{3, 2}中的2对应的联盟， 根据max[2]=120和avg[2]=79， 只从{1, 3}(90)、{1, 4}(80)、{1, 5}(90)、{2, 3}(90){2, 5}(120)、{4, 5}(110)中选取。因此， 较快找到势结构{2, 3}对应的最优联盟结构{{1, 3}，{2, 4, 5 }}和{{4, 5}，{1, 2, 3 }}， 值都为270。

势结构{3, 1, 1}中的3对应的联盟， 根据max[3]=190， avg[3]=142， 只从{1, 2, 3}(160)、{1, 4, 5}(150)、{2, 3, 4}(150)、{2, 4, 5}(180)、{3, 4, 5}(190)中选取。而1对应的单联盟， 根据max[1]=60和avg[1]=40， 只从{1}(50)、{2}(40)、{5}(60)中选取。因此， 较快找到势结构{1, 1, 3}对应的最优联盟结构{{1}, {2}, {3, 4, 5 }}， 值为280。

势结构{2, 2, 1}中的2对应的联盟， 根据max[2]=120和avg[2]=79， 只从{1，3}(90)、{1, 4}(80)、{1, 5}(90)、{2, 3}(90)、{2, 5}(120)、{4, 5}(110)中选取。而1对应的单联盟， 根据max[1]=60和avg[1]=40， 只从{1}(50)、 {2}(40)、 {5}(60)中选取。因此， 较快找到势结构{1, 2, 2}对应的最优联盟结构{{2}, {1, 3}, {4, 5}}(40+90+110=240)。

势结构{1, 1, 1, 2}中的2对应的联盟， 根据max[2]=120和avg[2]=79， 只从{1, 3}(90)、{1, 4}(80)、{1, 5}(90)、{2, 3}(90)、{2, 5}(120)、{4, 5}(110)中选取。而1对应的单联盟， 根据max[1]=60和avg[1]=40， 只从{1}(50)、{2}(40)、{5}(60)中选取。因此， 较快找到势结构{1, 2, 2}对应的最优联盟结构{{1}, {2}, {5}, {1, 3}}(50+40+60+90=240)。

对比得到， 本例的最优联盟结构为{{1}, {2}, {3, 4, 5 }}， 值为280。经表2统计， 搜索空间减少44%。

表2　n=5时优化前后的联盟结构计算量对比

4算法的基本信息对比

表3　各算法的基本信息对比

任一时间算法是指算法可以在任意时间中止，返回一个解，并随着时间的增加，解更优，其相对于非任一时间算法具有更好的实际应用。搜索单位可以是层、势结构、联盟组合或联盟结构结点等。搜索路径是否受联盟值影响也是衡量算法通用性的一个重要方面，一些算法的搜索路径是固定不变的，另一些则根据给定的联盟值的不同而发生变化。限界表示在最坏情况下搜索得到的局部最优解的质量。各算法的基本信息对比，如表3所示。

5结语

DP算法[9]利用最优联盟结构问题的最优子结构性质和重叠子问题性质，通过避免寻找整个空间来保证最优解，速度较快，时间复杂度为O(3n)，但是它不能够在任一时间产生解，要在内存中保留具有2n-1个输入的三张表。对于中等规模数量(大于26)的Agent，DP方法很快地变得不适用。如果试图通过限制能被形成的联盟的大小来减少问题的复杂性，从而使返回解的速度加快，然而，这样的限制也大大地减少了可能解的有效性，因为在这种情况下被选择的解可能任意地远离最优解。大多数的DP算法和启发式算法的搜索路径与给定的联盟值有关，或者是在满足一定的假设条件的前提下提出的[12-14]，当没有任何启发信息的条件下，只能选择搜索路径不受联盟值影响的算法。文中的算法与联盟值有关，首先要求输入所有2n-1个联盟的值，需要进行2n-1次赋值运算，在实际应用中也只对较小的n有效。其中势结构计算的时间复杂度为O(n2)，算法保留的联盟数多少与给定的联盟值信息有关，进一步的优化计算可以将搜索空间减少近一半。

目前研究中的一些进展包括：一是不以层为搜索单位，而以更小的搜索粒度，如势结构、联盟组合等进一步减少搜索的结点数，从而加快搜索；二是研究给定联盟值的情况，如何充分利用这些信息减少搜索空间；三是给定限界的情况搜索算法的进一步优化；四是对已提出算法之间的更详尽的比较分析。这些进一步的研究工作都值得期待。

参 考 文 献

[1]Sandholm T W, Larson K, Andersson M, et al. Coalition Structure Generation with Worst Case Guarantees[J]. Artificial Intelligence, 1999,111(1-2):209-238.

[2]Talal Rahwan,Tomasz P, Michalak, et al. Coalition structure generation: A survey[J]. Artificial Intelligence,2015, 229:139-174.

[3]詹宇森.多Agent合作博弈中的计算复杂性及相关算法研究[D].南京:南京大学,2013.

[4]胡山立,石纯一.给定限界要求的联盟结构生成[J].计算机学报,2001,24(11):1285-1290.

[5]Dang V D, Jennings N R. Generating coalition structures with finite bound from the optimal guarantees[C]//Proceedings of the 3rd International Joint Conference on Autonomous Agents and Multi-Agent Systems. New York:AAMAS,2004:564-571.

[6]Su She-Xiong, Hu Shan-Li, Zheng Sheng-Fu,et al.Coalition Structure Generation with Given Required Bound based on Cardinality Structure[C]// Proceedings of the 6th International Conference on Machine Learning and Cybernetics.Hong Kong:ICMLC,2007: 2505-2510.

[7]胡山立,石纯一,李少芳.给定限界的势结构分组与联盟结构生成[J].计算机学报, 2012,35(12):2618-2624.

[8]刘惊雷,童向荣,张伟.一种快速构建最优联盟结构的方法[J].计算机工程与应用,2006,42(4):35-44.

[9]张新良,石纯一.多Agent联盟结构动态生成算法[J].软件学报,2007,18(3):574-581.

[10]陈少白,张嫚,胡朝娣.赋权合作博弈中的可行联盟结构与收益分配[J].武汉科技大学学报,2015,38(1):77-80.

[11]王晓东.计算机算法设计与分析 [M]. 4版. 北京:电子工业出版,2012.

[12]刘惊雷,张伟,童向荣,等.一种O(2.983n)时间复杂度的最优联盟结构生成算法[J]. 软件学报,2011,22(5):938-950.

[13]Rahwan T, Jennings N R. An Improved Dynamic Programming Algorithm for Coalition Structure Generation[C]// Proceedings of the 7th international conference on Autonomous Agents and Multi-Agent Systems. Estoril: AAMAS, 2008:1417-1420.

[14]Panagopoulos, Athanasios Aris, Chalkiadakis, et al. Towards optimal solar tracking: a dynamic programming approach[C]// Proceedings of the 29th AAAI Conference on Artificial Intelligence.Austin, US: AAAI,2015:695-701.

Coalition Structure Generation Optimization Related to Coalition Value

LI Shaofang

(Information Engineering College, Putian University, Putian 351100, China)

AbstractThe coalition structure generation algorithm based on cardinality structure has nothing to do with the coalition values, which results can be applied to the coalition structures generated in optimization related to the coalition value. Meanwhile, in the study of problems related to the coalition value, people can make full use of the given coalition values information for further optimal calculation and improve efficiency. The paper introduces the information extraction method of coalition values with same cardinality, giving application examples, and reducing the nearly half search space.

Key wordsmulti-agent; coalition structure; cardinality structure ; algorithm optimization; coalition value

文章编号：1009-0312(2016)01-0015-05

中图分类号：TP393

文献标识码：A

作者简介：李少芳(1971—)，女，福建福安市人，副教授，硕士，主要从事计算机算法及多Agent系统研究。

基金项目：福建省科技厅资助项目(2015H0033)；福建省教育厅资助项目(JK2015041)。

收稿日期：2015-10-12