立式圆柱薄壳容器的振动特性研究

郑运虎,李　颖

(1.兰州理工大学石油化工学院， 甘肃　兰州　730050；2.四川省简阳市高级职业技术中学，四川　简阳　641400)



立式圆柱薄壳容器的振动特性研究

郑运虎1,李颖2

(1.兰州理工大学石油化工学院， 甘肃兰州730050；2.四川省简阳市高级职业技术中学，四川简阳641400)

摘要：为降低原油储罐的振动效应，防止其结构的局部破坏，对立式圆柱薄壳容器的振动特性进行研究。通过ANSYS Workbench软件对薄壁储罐分别进行空罐、半罐和满罐3种状态的不同约束方式的模态分析。分析结果表明：储罐的各阶振型与固有频率的大小有关；振型的变化则与激励方向密切相关，不同方向的激励所导致的振型差异较大；在满罐状态下的固有频率值最小，在低频的激励载荷下容易发生振动，但危害较小；摆振是造成罐顶破坏的重要原因，可通过在顶端增加约束的方法来削弱摆振以提高结构的稳定性。

关键词：预应力；薄壳；垂荡振动；模态；振型；满罐；约束

在海洋平台上服役的压力容器长期受到风浪载荷的冲击，会造成平台的垂荡和涡激振动。许多平台通过增加垂荡板以增加垂荡阻尼来减小垂荡振动,或者通过安装螺旋侧板来减小涡激振动。虽然这些措施能提高平台工作的稳定性，但平台的晃荡无法从根本上消除。实践证明， Spar平台上安装螺旋侧板最多能降低60%的激荡[1]。固定在平台上的构件的稳定性通常也受到平台振动的影响。研究表明，储罐罐顶的破坏通常是因为罐内液体的晃动造成对罐顶的反复冲击而引起的[2]。了解储罐结构的固有频率与振动特性, 可为防止结构振动的疲劳破坏[3-4]、评价结构的稳定性和优化结构设计提供一定的依据[5]。本文运用Workbench Acoustic Extension模块对盛装满罐原油、半罐原油和空罐3种状态下的储罐进行模态计算，探究不同约束条件下储罐的振动特性，以期为降低原油储罐的振动效应和防止结构的局部破坏提供一定参考。

1模态分析理论基础

1.1　经典动力学方程

由经典力学理论[6-13]可知，物体的动力学通用方程为

(1)

式中：[M]是质量矩阵；[C]是阻尼矩阵；[K]是刚度矩阵；{x}是位移；{F(t)}是力矢量；{x′}是速度矢量；{x′′}是加速度矢量。无阻尼模态分析是经典的特征值问题，动力学问题的运动方程为

(2)

1.2　改进后的动力学方程

盛装液体容器模态分析计算通常采用虚拟质量法[9]，其计算方程为

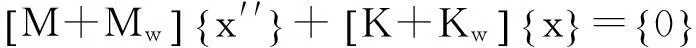
(3)

通过式(2)与式(3)对比不难发现质量矩阵增加了液体作用产生的附加质量矩阵[Mw]，而刚度矩阵增加了液体对结构产生的附加刚度矩阵[Kw]。对结构作用产生的附加刚度相对结构本身非常小，一般忽略，所以式(3)可改写为

(4)

假设流体为理想流体，即流体各向同性、不可压缩、无黏性，考虑结构重力的影响，在结构低速运动条件下，根据流体力学连续方程、运动方程和能量方程，结合Laplace方程与Helmholtz方程，可以求得速度势以及压力场的有限元方法的解析解：

(5)

(6)

(7)

F为节点上的压力。结合牛顿第二定律得：

(8)

(9)

结合式(7)、(8)、(9)得虚拟质量矩阵

(10)

式中：[Mw]为虚拟质量矩阵；[γ]为节点矩阵；[λ]为特征值矩阵，即固有频率。

2建立有限元模型

采用SolidWorks进行3D建模。建模过程中忽略管接头、孔、法兰、接管、垫板支座、加强圈和其他附属构件。模型简化为对称模。为便于查看，在Workbench中施加的载荷、力学计算结果以及网格划分结果均显示模型一半。容器材料为16MnR，直径为1.5 m，圆柱段长4 m，全长4.375 m，壁厚为5 mm；容器一端采用标准椭圆封(a/b=2)，另一端为平板封头，材质均为16MnR，壁厚5 mm，a=1.5 m，b=750 mm；模型材料为原油，直径为1.5 m，筒体长4 m。圆柱薄壳和液体模型采用六面体主导划分网格，封头网格采用Patch Conforming划分，封头与罐体接触部位网格细化。网格最终划分结果为29万4 360个节点，7万1 732个单元。具体划分情况见图1。

图1　有限元模型

3模态分析过程

3.1　静力学计算

在分析之前先建立16MnR和原油的材料属性，并将材料赋予模型。考虑静压力与重力，由于软件在湿模态求解模块中无法施加力学载荷，为更真实地模拟模态情况，所以将液体压力与重力以预应力的方式预先加载到结构上。图2为施加的梯度载荷，图3为静水压强计算结果。罐内存在油和气两相介质，由于气压较小，故忽略了气体的压力。

图2中的静水压强从顶端往底端逐步增大。可看出，载荷值随着盛油深度逐渐增大，最大载荷值为0.052 92 MPa，与理论计算一致。图3为静水压强下结构应力分布情况，最大应力值随梯度载荷值逐渐变大，符合静水压强应力变化规律，最大应力值为8.113 MPa靠近容器底端。容器材料最低屈服强度为345 MPa，满足强度要求。

图2　梯度载荷

图3　应力分布

3.2　模态计算

在Workbench extensiong 模块中将流体模型命定为Acoustic Body。在Acoustic Body属性中，完成以下设置：油液密度为9×10-7kg/mm3；声波在液体中传播速度为1.35 km/s;算法为对称耦合；FSI面为固液交界面；自由页面为液顶端面；默认采用流场为拉格朗日场；重力加速度为9.80 m/s2;定义求解阶数为6。计算时通过插入APDL命令，模块会自动将静水压力加载到结构上。完成设置后，开始模态计算。

模态计算结果由固有频率和振型2大部分组成。固有频率值的大小反映了结构的刚度和抗振能力。固有频率越大表示结构刚度越大，抗振能力越强，稳定性越高。计算结果表明，前6阶振型两两相似，即第1、2阶振型相似，第3、4阶振型相似，第5、6阶振型相似。为一目了然地了解各振型特点，分别截取了满罐底端约束、半罐底端约束、空罐底端约束、满罐两端约束、半罐两端约束和空罐两端约束共6种情况下的第1、3、5阶振型云图。图4示出储罐底端固定、顶端自由状态时原油满罐、半罐和空罐时的振型情况；图5为储罐底端固定、顶端铰支时原油满罐、半罐和空罐状态下的振型云图。图6和7为在各阶频率的不同状态和不同约束下的结构最大位移响应图和固有频率图。

(a)满罐第1阶振型 (b) 满罐第3阶振型 (c)满罐第5阶振型

(d)半罐第1阶振型 (e)半罐第3阶振型 (f)半罐第5阶振型

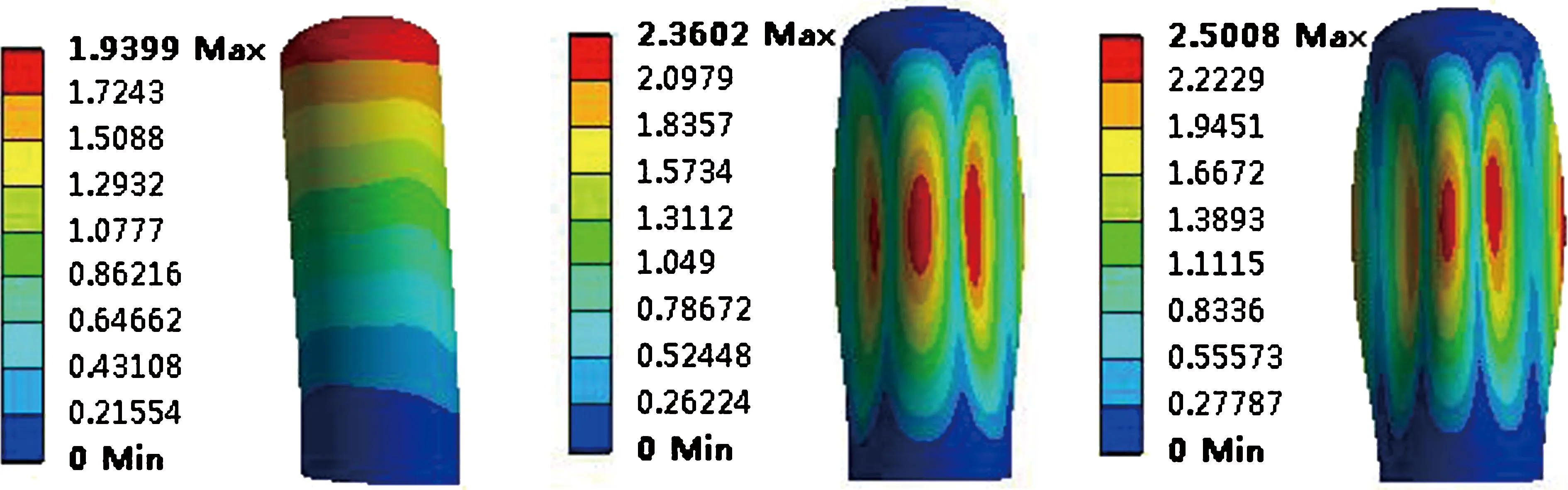
(g)空罐第1阶振型 (h)空罐第3阶振型 (i)空罐第5阶振型

图4储罐底端固定、顶端自由状态时的振型情况

(a)满罐第1阶振型 (b)满罐第3阶振型 (c)满罐第5阶振型

(d)半罐第1阶振型 (e)半罐第3阶振型 (f)半罐第5阶振型

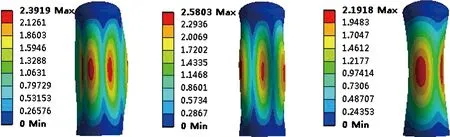
(g)空罐第1阶振型 (h)空罐第3阶振型 (i)空罐第5阶振型

图5储罐底端固定、顶端铰支时的振型情况

图6　各阶振型的最大振幅

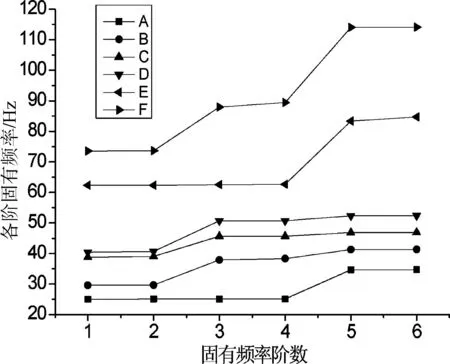
图7　不同状态下的各阶固有频率

从各阶云图中可以看出振型主要以轴向挤压、来回摆动和周向挤压为主。从图4可以看出：储罐整体在横向激励和纵向激励下出现轴向挤压、周向挤压和平面上来回摆动的振型特点；满罐和半罐时的1阶振型均沿轴向出现3个失稳波；满罐时的3阶振型、半罐时的5阶振型和空罐时的1阶振型均是摆振；满罐时的5阶振型和空罐时的3阶振型上升为4个失稳波；半罐时的3阶振型为周向挤压，出现2个失稳波；空罐时的5阶振型上升为轴向5个失稳波。从图5可看出：约束加强后，摆振消失了；满罐、半罐和空罐的1阶振型沿轴向均出现了4个失稳波，比储罐在底端约束和顶端自由时多了失稳波；满罐体的3阶、半罐的5阶和空罐的3阶振型均出现了5个失稳波；满罐5阶、半罐的3阶和空罐的5阶振型均是在周向的激励下出现了2个失稳波。各状态下的各阶振型云图不仅反映出结构在不同频率下的振动形态，而且可看出振型所对应频率下的激励载荷形式。通过储罐的振型特点，可看出激励载荷主要是周向激励、沿轴向的激励和整体横向载荷激励。其中整体横向激励是导致摆振的原因，周向和沿轴向的激励导致振型出现失稳波。

图6是储罐在满罐、半罐和空罐时在不同约束下的最大位移响应图。线1和线2反映的是储罐在满罐状态时底端固定、顶端自由和底端固定、顶端铰支状态下的各阶振型的最大位移响应曲线；线3和线4反映的是储罐在半罐状态下，底端固定、顶端自由和底端固定、顶端铰支时的各阶振型的最大位移响应曲线；线5和线6反映的是空罐状态下储罐底端固定、顶端自由和底端固定、顶端铰支时各阶振型的最大位移响应曲线。通过对比不难看出：储罐在两端均约束时的最大响应位移普遍比只约束底端时的大；随着储罐中油液深度的加深，各阶振型的最大振幅逐渐变小，即满罐时的罐体各阶振型的最大振幅<半罐时罐体各阶振型的最大振幅<空罐时罐体各阶振型的最大振幅。

图7反映的是满罐、半罐和空罐状态在不同约束条件下的各阶频率值。线A表示满罐状态下罐体底端固定、顶端自由时的各阶频率值曲线；线B表示满罐在罐体底端固定、顶端铰支时的各阶频率值曲线；线C表示半罐状态下罐体底端固定、顶端自由时各阶固有频率曲线；线D表示半罐状态下罐体底端固定、顶端铰支时各阶固有频率曲线；线E表示空罐状态下罐体底端固定、顶端自由时各阶固有频率曲线；线F表示空罐状态下罐体底端固定、顶端铰支时各阶固有频率曲线。从图上不难看出：各状态下各阶固有频率呈现出良好的递增规律，即状态A的各阶固有频率值<状态B的各阶固有频率值<状态C的各阶固有频率值<状态D的各阶固有频率值<状态E的各阶固有频率值<状态F的各阶固有频率值;罐体两端约束时的固有频率值大于一端约束时的固有频率值,即空罐状态下的固有频率值>半罐状态下的固有频率值>满罐状态下的固有频率值。

4结束语

本文以盛装原油的圆柱薄壳储罐为例，对储罐在满罐状态、半罐状态和空罐状态的不同约束方案下分别进行了模态计算。通过计算得到以下结论。

1)储罐的各阶振型与固有频率值的大小密切相关，不管储罐处于哪种状态，只要固有频率接近那么它们的振型也很相似。通常情况下固有频率越高振幅越大，振型的变化与激励的方式有关，激励频率高低与振型没有必然的联系。

2)储罐在满罐状态下的固有频率值最小，在低频的激励载荷下最容易发生振动；空罐状态的各阶固有频率值最大，说明空罐发生共振需要较高频率的激励载荷。

3)罐体在底端固定和顶端铰支约束下的各阶固有频率值比底端固定和顶端自由约束条件下的各阶固有频率值大，说明两端约束条件下结构的整体抗振性能有所提高。摆振是造成罐顶破坏的重要原因，所以增加约束，削弱摆振可以提高结构的稳定性。

4)根据所得的固有频率与相应的振型，可通过在相应位置增加阻尼和约束或在振型最大处加强结构以提高刚度，防止和避免共振带来的危害。

参考文献

[1]郭斌，唐文勇.Spar平台疲劳评估方法研究[D].上海:上海交通大学,2005.

[2]张光浩,崔文勇.储液罐动态响应及隔震分析研究[D].北京：北京化工大学,2010.

[3]姚起杭,姚军.工程结构的振动疲劳问题[J]. 应用力学学报,2006 (1):12.

[4]袁安富,陈俊.ANSYS在模态分析中的应用[J].中国制造业信息化,2007(11):42.

[5]杨康,韩涛.ANSYS在模态分析中的应用[J].佳木斯大学学报,2005,23(1):81.

[6]陈艳霞，陈磊.ANSYS Workbech工程应用与案例精通[M].北京: 电子工业出版社, 2012:25-35.

[7]张立翔.流体结构互动理论及其应用[M]. 北京: 科学出版社,2004：12-45.

[8]仲维国,张嘉钟.导弹静模态的ANSYS有限元分析[J].强度与环境,2004 (1):17.

[9]张洪才.ANSYS14.0 理论机械与工程应用实例[M].北京: 机械工业版社, 2012:25-56.

[10]贾锐,石秀华,徐宇明，等.基于ANSYS的圆柱薄壳结构模态分析[J].弹箭与制导学报,2008, 28(6):314.

[11]曹银萍,石秀华.基于ANSYS的鱼雷有限元建模与模态分析[J].弹箭与制导学报,2009,29(3):289.

[12]刘晓欧,尹韶平,严光洪.基于MSC Nastran的下环肋圆柱壳体振动模态计算方法[J].计算机辅助工程,2006,15(9):124.

[13]朱维兵,周刚,张海洋,等. 流体静压型机械密封轴向振动特性分析[J]. 西华大学学报(自然科学版),2014,33(1):1.

(编校：饶莉)

Research on the Vibration Characteristics of Vertical Cylindrical Shell Container

ZHENG Yunhu1, LI Ying2

(1.CollegeofPetrochemicalEngineering,LanzhouUniversityofTechnology,Lanzhou730050China;

2.JianyangSeniorVocationalandTechnicalSecondarySchool,Jianyang641400China)

Abstract:To reduce vibration effects of crude oil storage tank so that the local damage of its structure can be avoided, the vibration characteristics of vertical cylindrical shell containers are studied. On the ANSYS Workbench, we carried out the modal analysis for three sorts of thin-walled tanks. Some tanks are empty, and some tanks are filled with half tank of oil and the others are full. The results show that vibration type is associated with the tank natural frequency, and the vibration mode change is closely related to the excitation direction, and the difference of vibration modes from different direction excitation are distinct. Natural frequency of tank is minimum when the tank is full. Vibration occurs easily at low frequency but less harmful. Shimmy is an important cause of roof damage, and adding constraints at the top can reduce the shimmy to improve the stability of the structure.

Keywords:prestressing; thin cylindrical shell;heave vibration;modal; vibration modes;full tank;constraint

doi:10.3969/j.issn.1673-159X.2016.01.005

中图分类号：TE972

文献标志码：A

文章编号：1673-159X(2016)01-0024-05

基金项目：国家质检公益项目(201210026，201310152);甘肃省高等学校基本科研业务费(1205ZTC067)。

收稿日期：2014-12-16

第一作者：郑运虎(1986—),男,硕士,CAE工程师，主要研究方向为承压设备安全可靠性。E-mail:921238461@qq.com

·机电工程·