光纤陀螺角速率延迟特性分析与测试

李星善，马 珣，袁慧铮，王 勇，陆俊清，葛仲浩

(1.湖北航天技术研究院总体设计所，武汉430040；2.湖北三江航天万峰科技发展有限公司，湖北 孝感432000)

光纤陀螺角速率延迟特性分析与测试

李星善1，马 珣2，袁慧铮1，王 勇1，陆俊清1，葛仲浩1

(1.湖北航天技术研究院总体设计所，武汉430040；2.湖北三江航天万峰科技发展有限公司，湖北 孝感432000)

在姿态控制系统中，作为传感器的陀螺所起的作用至关重要，尤其是在系统动态环境比较恶劣的情况下，需要陀螺测量的载体旋转速度准确且满足实时性要求，否则会造成大的误差，严重时会造成姿态失控。针对某型惯测组合中的光纤陀螺，分析了测量延时产生的因素，提出了一种在转台上低采样频率情况下精确测量延时量的方法。通过实际试验，得到的结果与理论分析一致，验证了该方法的正确性和测量精度。

姿态控制；惯测组合；光纤陀螺；延迟特性

0 引言

惯性测量组合是惯性导航系统的核心部件，作为角速度和加速度传感器，其测量的精确性对系统的导航结果具有直接的影响。在导弹武器系统中，机动要求越来越多，复杂的弹道给姿态稳定控制提出了更高的要求。为满足一定的控制裕度，要求传感器的输出延时足够小，减少系统失稳的可能性。因此在惯测组合的设计过程中，需要考虑对输出延时的控制，减少数据转换的次数及数据处理所占用的时间，以提高系统的实时性。除了设计的保证，在平时的标定测试或一般功能测试中，由于没有参考基准，很难精确得出延时的具体数值。因此需要设计一种测量方法，对惯测组合的输出延时进行精确测量，并依据测量结果对软硬件设计进行验证并改进，逐步达到系统对延时的要求。

1 惯测组合的测量延迟分析

惯性测量组合一般由陀螺、加速度计及相应的处理电路组成，以某型光纤惯性测量组合为例，输出延时包括：光纤陀螺、石英挠性加速度计表头本身的测量延迟，处理电路造成的延迟，通信延迟等。惯测组合原理如图1所示。由于对石英加速度计通道的延迟已有成熟的研究结果，本文主要研究光纤陀螺通道的输出延迟。

图1 光纤惯测组合原理框图Fig.1 Functional block diagram of IMU based on fiber gyroscope

在光纤惯测组合中，光纤陀螺测量转速基于sagnac效应原理，如图2所示。敏感的相位误差ΔΦR=2πLD·Ω/λc，其中λ表示真空中的波长，c为真空中的光速，D表示线圈直径，L表示光纤线圈长度。可以看出根据sagnac效应，转速与相位差成正比关系，且是瞬时产生，可以认为原理上无延迟产生。

图2 真空情况下的Sagnac效应Fig.2 Sagnac effect in vacuum

在数据处理过程中，需要进行闭环处理，周期为光纤环的渡越时间，即光沿光纤线圈传播的时间，以1 000m光纤环为例，本征周期约为3.4μs，考虑到闭环处理中方波调制，AD采样存在延迟，大约为1个处理周期，再加上积分计算，在达到输出模块时延时不会超过2个本征周期。在光纤陀螺中，数据输出采用脉冲方式，更新周期为0.5ms，因此会引入不超过1个周期的延迟。由于输出周期远大于陀螺闭环的本征周期，闭环延迟可以忽略，所以陀螺理论输出延迟在0～0.5ms之间。

除了陀螺本身的延迟，数据处理板的计算以及通信也会造成最终的测量延迟。以某型光纤惯测组合为例，数据处理板完成陀螺脉冲的采样、实时温度补偿、打包发送等功能，系统工作频率10MHz。其中脉冲采样可以在1个处理周期内完成，温补在10个周期左右完成，延时不超过0.1ms。惯组输出串行通信速率为1MHz，31个字节，约2 000个周期可以完成不超过0.2ms，因此理论上惯组信号处理板的延迟在0.3ms左右。

综上所述，光纤惯测组合陀螺通道的测量延迟包括陀螺表头延迟和数据处理板延迟，大约在0.8ms以内。

2 测量方案

为准确测量光纤陀螺的延时特性，需要使用精密转台作为基准，并对测角精度和实时性有较高的要求。其中测角精度应不小于陀螺的分辨率，陀螺稳定精度为0.5(°)/h，本单位某型三轴转台0.36″的测角精度可以满足10(°)/s摇摆时测量要求。

图3 惯测组合延时特性标定连接图Fig.3 Design chart for delay characteristics measurement

按图3所示，将惯测组合固联安装在三轴转台内框上，使用一块采样板对惯组数据和转台并口测角数据同时进行采集。这里采样板程序中使用了公共时间计数器，使得接收到的惯组数据和转台测角数据共用一个时间信息，实现了时间的同步。采样板接收到惯组数据和转台测角数据后，读取时间计数器，并打包发送到上位机处理。

该方案中惯组采样周期为2ms，转台采样周期为1ms。使用频率1Hz，幅值3°和频率0.1Hz，幅值10°的摇摆参数分别对各个输入轴进行测试，在上位机上得到了有效的试验数据，通过处理得到准确的陀螺通道延时量。

采用1Hz，3°和0.1Hz，10°时，角度曲线分别为A=3·sin(2π(t-t0))和A=10·sin(2π·0.1(t-t0))。选用的光纤陀螺精度为0.5(°)/h，当采用1Hz，3°试验条件时，每周期的测角精度约为1.4E-4(°)，代入角度曲线，可辨识的最小时间差为7.4μs。同理采用0.1Hz，10°试验条件时，可辨识的最小时间差为0.2ms，对测试数据进行多周期拟合，测试精度可达到0.1ms以内。

3 测试数据分析

在X轴频率0.1Hz，幅值10°的摇摆试验中，对测得的转台角度进行归一化处理，并使用最小二乘法对正弦角度进行拟合，结果如图4所示。拟合曲线与测试曲线重合，在该时间轴上，周期为10000.0837ms，相位为-1865.3085ms。

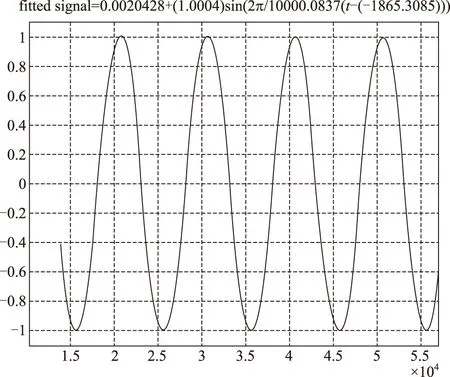
图4 转台角度归一化拟合曲线Fig.4 Fitting curve of the angle of turn table in normalization method

对X陀螺输出数据进行归一化处理，由于陀螺输出的是脉冲角增量，为了与转台角度进行对应，对角增量进行积分处理，得到如图5所示细线条曲线。由于没有扣除陀螺零偏和试验时的地速分量，造成曲线向正方向发生偏移，而不是标准的正弦曲线；扣除零偏和地速分量，重新处理后为图5所示粗线条曲线，为标准正弦曲线。

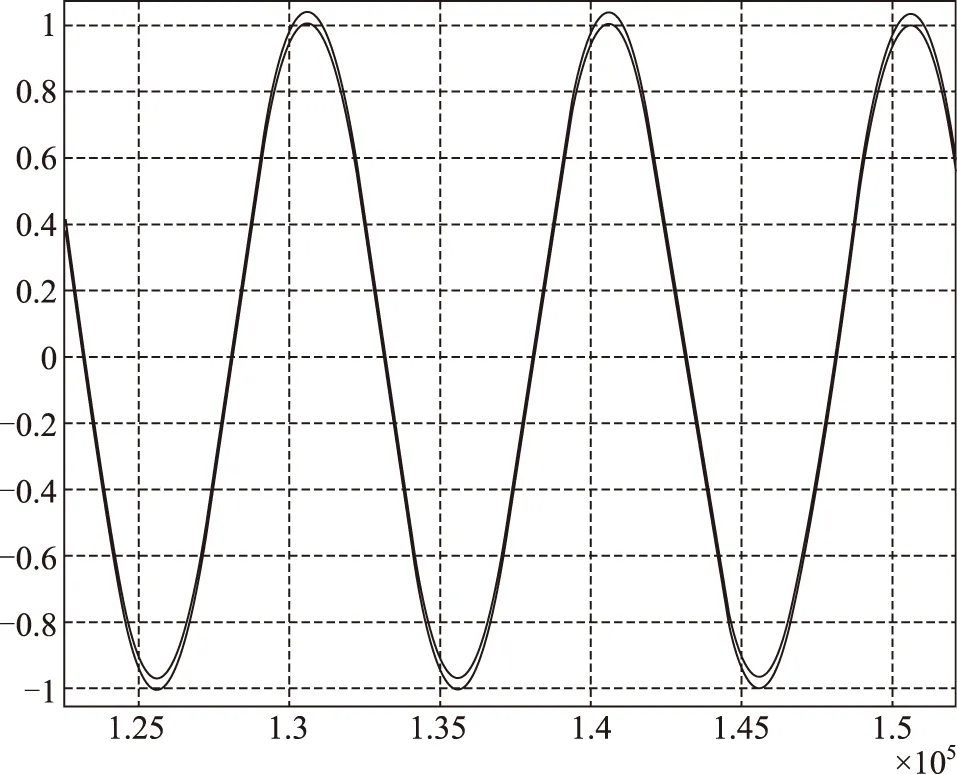
图5 陀螺输出数据归一化处理Fig.5 The output of fiber gyroscope in normalization method

采用最小二乘法对处理后的陀螺数据进行拟合，得到图6所示曲线。拟合曲线与测试曲线完全重合，在该时间轴上，周期为10000.0859ms，相位为-1864.8427ms。

图6 陀螺数据拟合曲线Fig.6 Fitting curve of the output of fiber gyroscope

转台测角数据和陀螺积分角度采用同一个时间计数器，所以拟合正弦曲线相位具有可比性，零点差值为角度延迟量。假设角度归一化曲线为A=sin(t-t0)，求导为角速率曲线W=cos(t-t0)，可见角度与角速率的零点位置相同，角度的零点差值即为角速率延迟量。

从数据可以看出，转台角度和陀螺积分角度的拟合周期只相差0.0022ms，在4.9min的测试数据中可以忽略。转台角度超前惯组输出0.4658ms。考虑转台测角延迟0.05ms，惯组实际延时量为0.5158ms。惯测组合数据处理板造成的延迟可以在电路板上直接测量获得，实测为0.28ms。因此陀螺本身的延迟为0.2358ms。

同理对X轴频率1Hz，幅值3°的摇摆试验数据进行处理，如图7、图8所示。

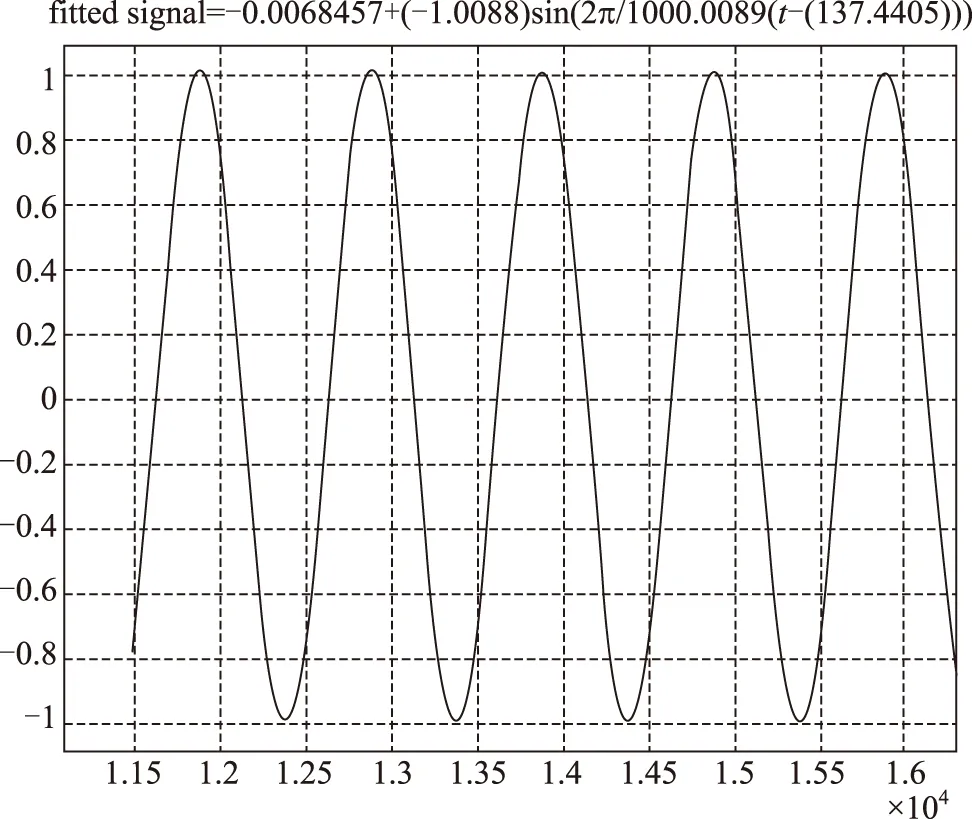
图7 转台角度归一化拟合曲线Fig.7 Fitting curve of the angle of turn table in normalization method

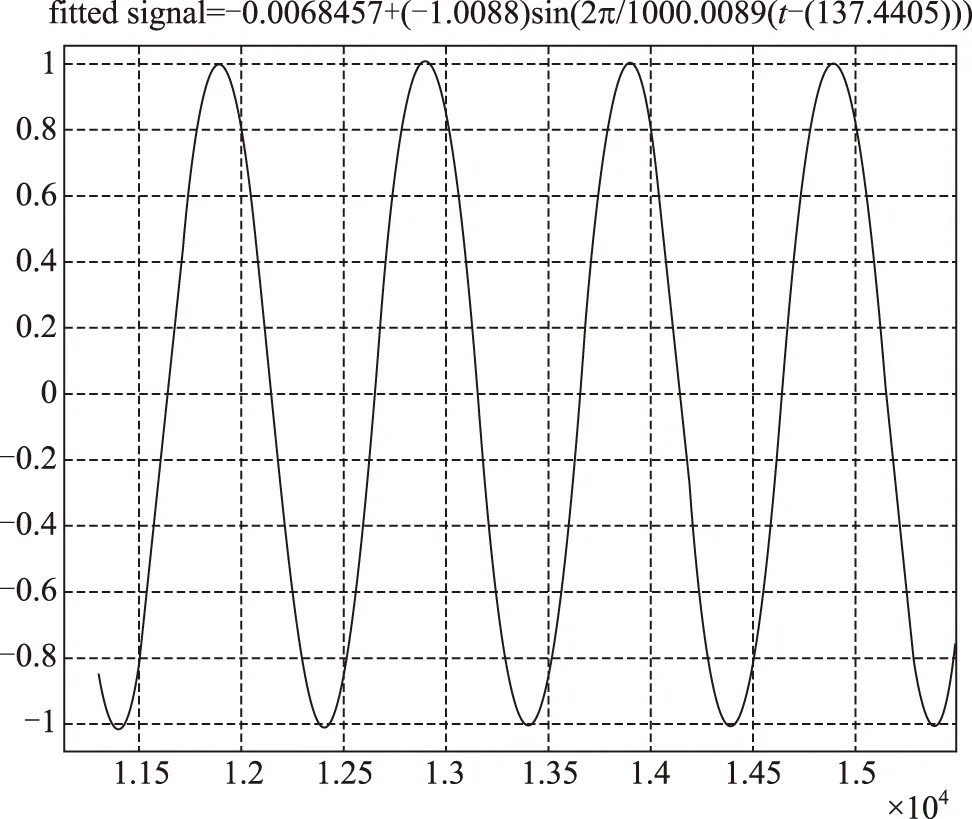
图8 陀螺数据拟合曲线Fig.8 Fitting curve of the output of fiber gyroscope

可见数据拟合良好，增加测角延迟0.05ms，扣除数据处理及通信延迟0.28ms，陀螺本身延迟为0.2967ms。与0.1Hz，幅值10°测试结果基本相同。

对另外两个输入轴进行测试，陀螺延迟均在0.2～0.4ms之间，与分析结果一致。

4 结论

在光纤陀螺的延时特性测试中，采样板使用同一时间计数器同步惯组数据和转台角度，省去了硬件同步设计，方案实现简单。由于采用相同的时间，数据处理时得到的相位可直接相减，且进行了惯组数据积分、归一化正弦拟合等处理，有效利用了全部采样数据，得到了精确的相位信息，实现了低采样速率下对惯测组合延时量的精确测量。

以光纤惯测组合为例进行了延时的理论分析和实际测试，使用该方法测试结果重复性好，与理论分析结果吻合，验证了测试方法的正确性和测量精度。

[1] Wang Yan.Research on control characteristics of digital closed-loop FOG[D].Beijing：School of Astronautics，Beijing University of Aeronautics and Astronautics，2004.

[2] Gaiffe T.From R&D brassboards to navigation grade FOG-based INS the experience of photonetics ixsea[J].IEEE0-7803-7289-1/02，2002：1-4.

[3] Herve C.Lefevre.张桂才，王巍，译.光纤陀螺仪[M].国防工业出版社，2002.

[4] 王巍.干涉型光纤陀螺仪技术[M].中国宇航出版社，2010.

[5] 张桂才.光纤陀螺原理与技术[M].国防工业出版社，2008.

Analysis and Test for Angular Rate Delay Characteristics of Fiber Optic Gyroscopes

LI Xing-shan1，MA Xun2，YUAN Hui-zheng1，WANG Yong1，LU Jun-qing1，GE Zhong-hao1

(1.The 9th Designing of China Aerospace Science Industry Crop，Wuhan 430040，China；2.Hubei Sanjiang Space Wanfeng Technology Development Co.，Ltd.，Xiaogan 432000，China)

The function of gyroscope is very important in attitude control system.High accurate and real-time output of rotational velocity of vector are crucial for a steady-state system in harsh dynamic environment，otherwise，the systematic error would appear，or even lead to loss of control.In this paper the cause of delay characteristic for FOG was studied，and the accurate measurement method in the case of low-frequency sample on test tables for delay differential was proposed.Finally，the precision and accuracy in the measuring method were verified by experiment，and the results were consistent with theoretical analysis.

Attitude control；Inertial measuring units；Fiber optic gyroscope；Delay characteristic

2015-03-18；

2015-09-02。

李星善(1982-)，男，高级工程师，主要从事光纤陀螺及其惯性系统的研究。E-mail：lxs4233@163.com

U666.1

A

2095-8110(2016)01-0069-04