一种基于实时物理闭环校正的空中动基座对准方法
何长久,许 静,高伟熙,唐子伟,王忠辉
(北京自动化控制设备研究所,北京100074)
一种基于实时物理闭环校正的空中动基座对准方法
何长久,许 静,高伟熙,唐子伟,王忠辉
(北京自动化控制设备研究所,北京100074)
提出了一种基于实时物理闭环校正的平台惯导空中动基座对准方法。该方法利用卡尔曼滤波实现惯导误差的实时估计,根据最优二次型准则设计反馈控制进行惯导平台的实时闭环物理校正,有效保证了对准精度。经机载试验,平台惯导空中动基座对准后,导航精度大幅提高。
高精度平台惯导;动基座对准;实时;物理闭环校正
0 引言
平台惯导动基座对准技术是非常重要的关键技术,主要解决在带飞状态下平台惯导空中启动及初始对准的技术问题。其动基座对准方案采用传递对准方式,基准信息为处于连续卫星修正状态的母惯导信息。依此为背景,设计一种基于实时物理闭环校正的空中动基座对准方法,实现了平台惯导系统在动基座条件下的高精度对准。
1 动基座对准方案
子惯导采用游移自由方位编排解算的高精度平台惯导系统,动基座对准基准信息为处于卫星连续修正状态下的母惯导信息。
兼顾对准时间和对准精度两方面考虑,采用“速度+位置”的匹配对准方式。
对于平台惯导,在动基座对准过程中需完成速度和位置误差修正、失调角误差估计、物理平台调整、陀螺漂移估计补偿。为此,设计了卡尔曼滤波器,在动基座对准过程中实时进行子惯导状态误差准确估计的同时,依据最优二次型准则确定的闭环控制反馈系数,实现物理平台的实时闭环校准。
1.1 干扰补偿方案
在惯导系统传递对准设计过程中,杆臂效应影响对准精度,设计考虑杆臂效应、挠曲振动等干扰因素的补偿和处理。
母、子惯导位置示意图如图1所示。母、子惯导相对惯性空间的距离矢量分别为rm和rs,母、子惯导之间的矢量距离为lms,当角速度为ω时,母惯导速度为
vmL=ω×rm
(1)
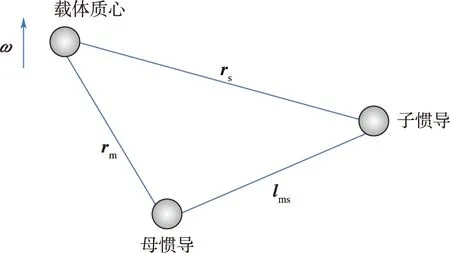
图1 母子惯导位置示意图Fig.1 The position diagram of themaster INS and the slave INS
子惯导速度为
vsL=ω×rs
(2)
母、子惯导之间的杆臂效应速度为
v杆臂=ω×rs-ω×rm=ω×lms
(3)
lms可以通过量测母子惯导之间的距离获得,ω可以通过平台姿态角获得,根据式(3),可以计算杆臂效应带来的速度v杆臂。杆臂效应在卡尔曼滤波器的速度量测值中进行实时补偿
Zk=vs-vm-v杆臂
(4)
1.2 卡尔曼滤波器
动基座对准过程中,用于子惯导误差参数估计的滤波器为经典卡尔曼滤波器,滤波器工作在实时闭环状态,其包含滤波周期、离散周期以及反馈修正周期的设定。子惯导误差模型为:
(5)
(6)
离散卡尔曼滤波算法如下:
(7)
(8)
(9)
(10)
Pk=(I-KkHk)Pk/k-1
(11)
为了兼顾对准时间和对准精度,在动基座对准方案中,共设计了两个卡尔曼滤波器,分别为5维和8维,5维滤波器实现对水平轴平台姿态角误差的粗估和修正;8维滤波器估计过程中,要求载体机动,以实现对方位姿态角误差的估计,并在此基础上,实现对水平姿态角误差的精确估计和修正、水平轴陀螺漂移的精确估计。
1.3 方位对准方案
平台惯导方位对准采用基于速度指向分解误差原理,采用机动方案,实现方位误差角的准确估计。
机动对准方案,需要载体进行一定时间(3~5min)的机动,影响方位精度的因素有:加速度计刻度系数误差、基准速度误差(主要为运动相关变化部分)、补偿后残存的杆臂效应误差。其对准精度的估算公式可用式(12)表示:
(12)
子惯导加速度计刻度系数误差量级为1×10-4(1σ)、基准速度误差运动变化量(载机机动按90°转弯)和杆臂误差补偿残余按0.2m/s(1σ)考虑,其寻北精度量级为:3′(1σ)。
通过仿真分析和比较,确定采用机动对准方案。方位对准精度与载机机动动作的大小、持续时间直接相关。机动形式有三种:S形机动、盘旋和转弯,通过仿真确定的三种机动形式要求为:
1)S形机动:机动最大加速度约为0.3~0.5g,机动周期不少于5min;
2)盘旋机动或转弯:载机盘旋一圈或进行一个90°转弯。
机动结束后,转入直线飞行,惯导完成精调平、水平陀螺漂移估计和导航参数初始化。
1.4 方位控制方案

方位轴直接工作在游移方位方式下,方位轴控制施矩公式为
(13)
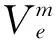
2 惯导误差校正
2.1 闭环反馈校正原则
卡尔曼滤波器进行惯导误差建模设计时,一般假定各项误差为小量,忽略了高次项误差的影响,误差模型传播近似为线性。采用开环校正方案时,由于物理平台处于非水平状态,对准阶段惯导误差增长较快,直接影响到惯导误差的估计精度;相对于开环校正,闭环反馈校正实时对惯导误差进行校正,惯导误差始终控制为小量,滤波器中惯导误差模型更为准确,误差估计精度也更高。
实时闭环反馈校正时,特别是滤波器工作初期,各误差参数估计均没有收敛,反馈校正不当将导致滤波器和物理平台处于震荡状态甚至失效,必须依据一定的准则,选择合理的校正系数。
本方法利用线性二次型最优控制准则,分析确定惯导误差实时物理闭环反馈校正系数。线性二次型最优控制原理如下。
设线性定常系统的状态方程为
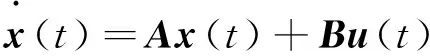
(14)
二次型性能指标为
(15)
式中,Q为正定(或半正定)实对称阵,R为正定实对称阵,xT(t)Qx(t)表示状态变量与平衡位置的偏差,uT(t)Ru(t)与控制功率成正比。
反馈控制过程中,使J最小,就是使系统的偏差最小,并使控制过程的消耗能量最小。可以证明,当系统的状态是完全可控时,使J最小的控制是状态X(t)的线性函数,即
u(t)=-Kx(t)
(16)
其中,
K=R-1BTP
(17)
P为常数对称阵定矩阵,且满足黎卡提代数方程
PA+ATP-PBR-1BTP+Q=0
(18)
由分离性定理可知,反馈修正环节可以单独设计。状态矩阵A取决与惯导误差模型,根据实际修正周期、滤波周期,综合考虑校正后的超调量和超调时间,按照二次型最优准则,确定反馈修正系数向量K。
2.2 惯导误差校正方案
根据不同误差项特性,选择不同的校正方案,具体如下:
(1)位置、速度误差校正
根据滤波器对子惯导位置误差、速度误差的估计,以50ms为周期,按照设定的反馈系数,实时在子惯导导航解算中扣除这两项误差。
(2)水平轴平台失调角校正
根据滤波器对子惯导水平轴平台失调角的估计,量纲转换后,以20ms为周期,按照设定的反馈系数,在平台施矩解算中扣除。
(3)水平轴陀螺漂移校正
陀螺漂移的估计时间较长,而且该值的估计精度受方位失调角影响较大,动基座对准过程中,不对水平轴陀螺漂移进行校正。动基座对准结束,以最后估计的水平轴陀螺漂移值为准,量纲转换后,在转导航后的导航施矩解算时,实时补偿陀螺漂移等效值。
(4)方位失调角校正
方位失调角估计是动基座对准的关键,该值的估计直接影响到水平轴失调角和水平轴陀螺漂移的估计精度。载机机动后方位失调角稳定收敛,但对准过程中,不对该值进行补偿。导航编排采用游移自由方位,动基座对准结束,转导航初始化时,直接在游移方位角初始值中扣除该值。
3 试验验证
基于实时物理闭环校正的高精度平台惯导系统空中动基座对准方法完成地面调试、车载试验、机载试验,机载试验情况如下。
参试子惯导为某高精度平台惯导系统,母惯导为处于连续GNSS卫星修正状态下的某高精度平台惯导系统。机动方式为正反90°曲线机动、90°自然转弯、绕机场盘旋三种。
按照上述对准方案设计,在机载试验中对误差估计效果、子惯导校正效果、对准后导航精度进行了全面考核。7个架次动基座对准后,子惯导纯惯性导航1h的精度优于1nmile(1σ),导航精度统计值如表1所示(基准信息为GPS卫星信息)。
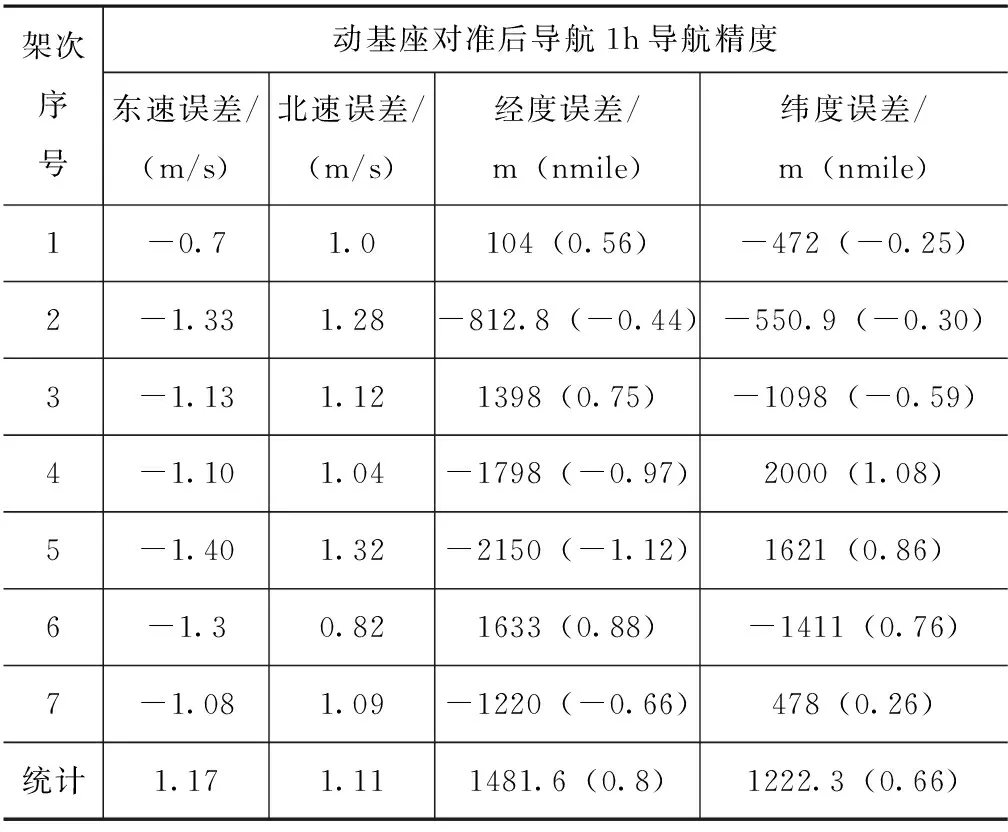
表1 动基座对准后子惯导纯惯性导航精度统计Tab.1 Inertial navigation accuracy statistc of slave INS after moving alignment
典型试验曲线如图2~图7所示。
分析试验数据可知:
1)载体机动后,方位失调角估计即可稳定收敛,收敛时间小于3min,方位失准角估计精度稳定且满足要求;
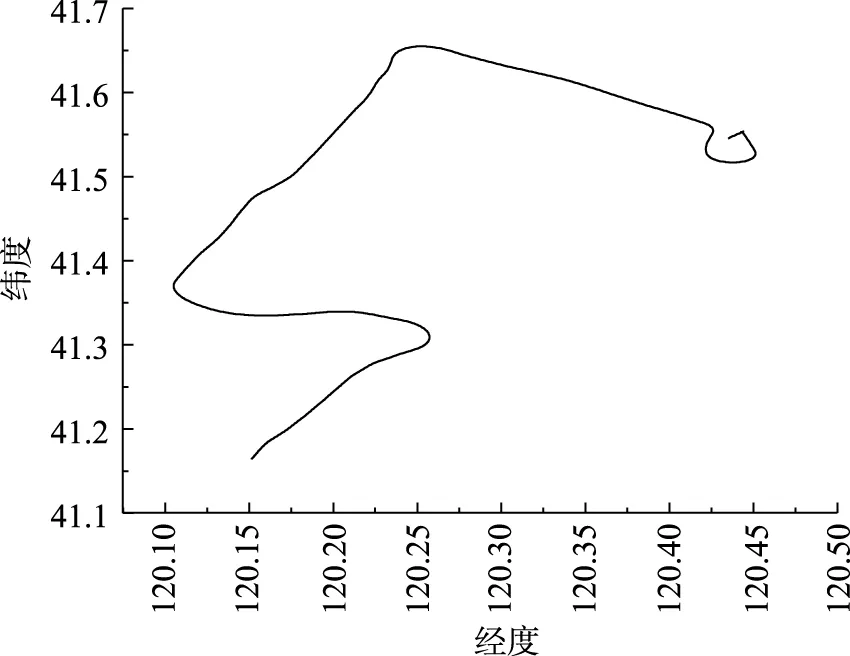
图2 机动航线Fig.2 Maneuver route
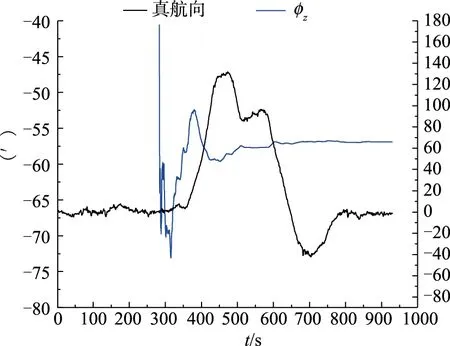
图3 对准期间方位失调角估计Fig.3 Estimation of azimuth misalignment angle during alignment
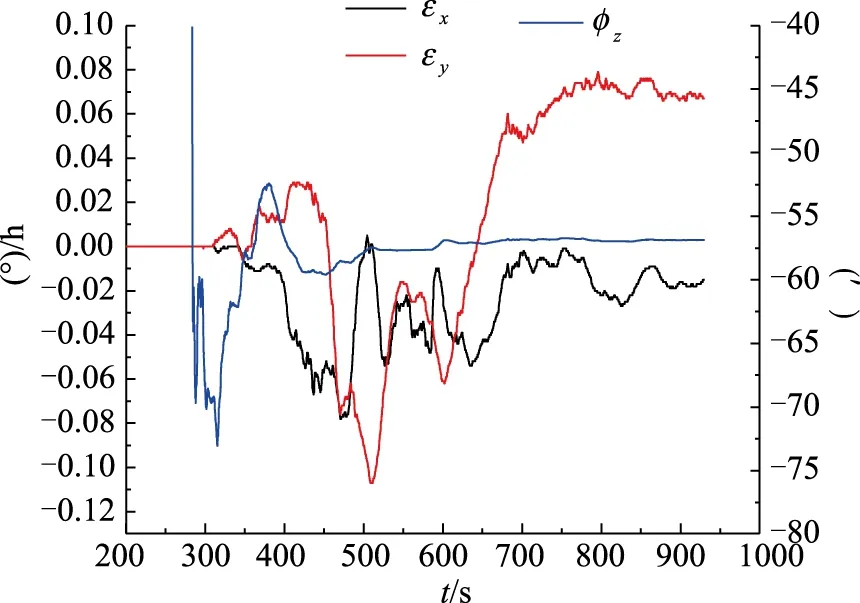
图4 对准期间水平轴陀螺漂移、方位失调角估计Fig.4 Estimation of gyro drift in the horizontal axis direction during alignment
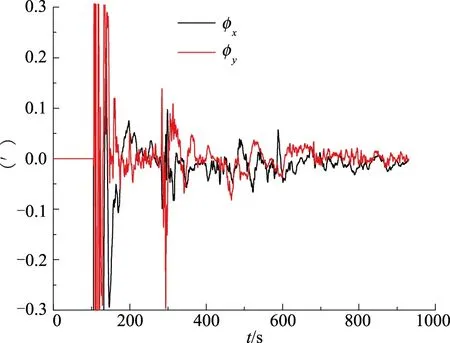
图5 对准期间水平轴平台失调角估计Fig.5 Estimation of platform misalignment angles in the horizontal axis direction during alignment

图6 对准后纯惯性导航速度误差曲线Fig.6 Velocity error curves chart of inertial navigation after moving alignment
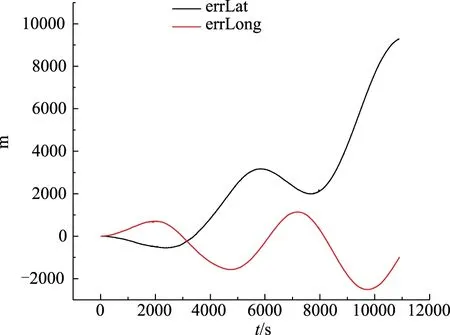
图7 对准后纯惯性导航位置误差曲线Fig.7 Location error curve chart of inertial navigation after moving alignment
2)方位失调角收敛后约300s,水平轴陀螺随机常值漂移估计可稳定收敛,估计精度0.01(°)/h左右;方位失调角收敛之前,方位失调角误差耦合到水平轴陀螺随机常值漂移中,水平轴陀螺随机常值漂移的估计能够收敛,但是估计精度将直接受到实际方位失调角影响;
3)平台水平轴失调角对准稳定时间小于100s,在方位失调角估计过程中,水平轴失调角有小幅度震荡,说明方位失调角估计精度对高精度平台惯导系统的水平轴失调角估计有一定的耦合影响。水平轴失调角再此稳定后,对准精度进一步提高,优于10″;
4)动基座对准下,按照上述设计方案,对准后1h导航精度优于1nmile(1σ)。
机载试验表明,基于实时物理闭环校正的空中动基座对准方法,对平台惯导系统的导航精度有大幅提高。
4 结论
本报告设计一种基于实时物理闭环校正的动基座对准方法,实现了高精度平台惯导空中启动、对准的工程方案。经机载试验验证,空中动基座对准后纯惯导1h导航精度优于1nmile(1σ),具有较高的工程应用价值。
[1] Titterton D H,Weston J L.Strapdown inertial navigation technology[M].USA:The American.Institute of Aeronautics and Astronautics and the Institution of Electrical Engineers,2004:342-344.
[2] Baziw J,Leondes C T.In-flight alignment and calibration of inertial measurement units,Part I:General formulation[J].IEEE Transactions on Aerospace and Electronic Systems,1972,8(4):439-449.
[3] 翁浚,秦永元,严恭敏,成研.车载动基座FOAM对准算法[J].系统工程与电子技术,2013,35(7):1498-1501.
[4] 严恭敏,翁浚,白亮,等.基于惯性参考系的动基座初始对准与定位导航[J].系统工程与电子技术,2011,3(3):618-621.
[5] 杨博,胡平华,敬军,弹用平台惯导系统空中动基座对准技术[J].惯性技术学报,2007,15(2):151-154.
[6] 刘百奇,宫晓琳,房建成.基于GPS 观测量和模型预测滤波的机载SINS /GPS 空中自对准[J].中国惯性技术学报,2007,15(5):568-572.
[7] 王司,邓正隆.机载导弹空中二次快速传递对准方法研究[J].航空学报,2005,26(4):486-489.
[8] Hong H S,Lee J G,Park C G.In-flight alignment of SDINS under large initial heading error[C]//AIAA Guidance,Navigation,and Control Conference an Exhibit,Montreal,Canada,AIAA-2001-4183.
[9] 冯培德,糜秀娣,徐仕会,等.惯导系统在动基座条件下对准的新途径[J].中国惯性技术学报,2001,9(4):28-31.
[10] 房建成,祝世平,俞文伯.一种新的惯导系统静基座快速初始对准方法[J].北京航空航天大学学报,1999,25(6):728-731.
An In-flight Moving Alignment Method Based on the Real Time Physical Closed-loop Correction
HE Chang-jiu,XU Jing,GAO Wei-xi,TANG Zi-wei,WANG Zhong-hui
(Beijing Institute of Automatic Control Equipment,Beijing 100074,China)
In this paper,an in-flight moving alignment method which is based on the real time physical closed-loop correction,applying to the platform INS is put forward.In this method,the real time estimation of inertial navigation error is realized by using Kalman filter,and a feedback control is designed according to the optimal quadratic criterion to do the real time physical closed-loop correction for the platform of INS,which effectively guarantees the alignment precision.The navigation precision can be improved after in-flight moving alignment,verifying by airborne flight experiments.
High precision platform INS;In-flight moving alignment;Real time;Physical closed-loop correction
2015-11-09;
2015-11-12。
国家自然科学基金项目—基于三轴惯性稳定平台的轻小型航空/海洋重力仪研究(41527803)
何长久(1989-),男,硕士,助理工程师,主要从事惯性导航方面的研究。E-mail:hechangjiuok@163.com
U666.1
A
2095-8110(2016)01-0019-06

