节点重要度在复杂网络鲁棒性中的应用

莫泓铭

(四川民族学院，四川康定 626001)



节点重要度在复杂网络鲁棒性中的应用

莫泓铭

(四川民族学院，四川康定 626001)

[摘要]如何评价网络的鲁棒性一直是当前的一个研究热点。识别网络中的重要节点从而梳理网络的体系结构有助于提高网络的可控性。近年来，有关识别复杂网络中重要节点的研究取得了一定的进展。基于此，本文提出了一种复杂网络中识别重要节点的方法来验证网络的鲁棒性。实例验证表明越重要的节点对网络鲁棒性的影响越大。

[关键词]复杂网络；重要节点；鲁棒性；脆弱性

随着大数据时代的到来，生活中的各种系统都可以被抽象为网络。我们的生活被各种各样的网络包围着，常见的如通信网络、在线社交网络、电力网络、交通网络、物联网等，在学术上它们都可以被视为复杂网络[1-4]。由于这些系统越来越庞大，结构越来越复杂，与人们的生活联系得越来越紧密，一旦其系统失效，将会对我们的生产、生活和经济发展带来不可估量的后果。复杂网络具自组织、自相似、吸引子、小世界、无标度中部分或全部性质[3-4]。近年来，复杂网络的可靠性与抗毁能力越来越受到广大学者的关注[5-7]。鲁棒性是用来表征控制系统对特性或参数摄动的不敏感性。在实际应用中，系统或网络面临的各种各样的主观或客观的干扰是不可避免的。近年来，对复杂网络鲁棒性的研究大多集中在网络中的边与节点。本文主要从复杂网络中节点重要度的视角来探讨复杂网络的鲁棒性。

1基础知识

自然界中存在的许多复杂系统都可以通过各种各样的网络加以描述。一个典型的网络可由许多的节点和节点之间边的关系构成。假如一个网络G=(V，E)是由|V|=n个节点和|E|=m条边组成[8]。vij=1表示节点i和节点j之间有一条连边，vij=0代表节点i和节点j不相连。

1.1复杂网络的基本特性[3-4]

复杂网络具有自组织、自相似、吸引子、小世界、无标度等特性，相对于一般意义上的网络而言，其“复杂”主要体现：(1)结构复杂。节点数目众多，网络结构特征呈现多样性与复杂性；(2)节点间关系错综复杂，对于加权网络，节点间的权重各异；对于有向网络且节点间的连边存在方向性；(3)对于时域或空域网络，节点的状态随时间或空间的变化而变化；(4)多重属性的融合。复杂网络中的节点、边、结构都具有多重的关系，因而很难简单地概括、掌握其结构。

1.2识别复杂网络中重要节点的算法

通过以上这些算法或指标可以单一地衡量节点某一个方面的能力，每种单一的算法都有其侧重点及局限性。基于此，学者们提出了一些多属性指标的综合计算方法，例如：Du[11]等综合考虑了节点的DC、BC和CC等指标，然后运用TOPSIS(technique for order performance by similarity to ideal solution)法来为每个节点确定了一个的综合指标，从而按最优解排序，据此得到节点的重要性排序结果。Wei[12-13]等利用证据理论[14-15]的思想将加权网络中节点的DC、BC和CC等指标视作BPAs(basic probability assignments)，结合证据理论的组合规则将这些BPAs进行融合，得到一个节点的综合BPA值，最终对节点的影响力进行排序。Mo[16]等基于证据理论的思想提出了一种在无权网络中融合节点的DC、BC和CC等指标的算法。度仅仅考虑的是节点的最相邻的邻居情况，认为度相同的节点则其同等重要，然而近来的一些研究表明，节点所处的位置也是非常重要的，即使一些处在核心位置的关键节点，虽然度很小，但它们却非常重要，而一些处在网络边缘的节点度很大，但影响力却很小。基于此，Kitsak[17]等提出了K-核分解法(K-shell decomposition)，通过网络分层的方法来确定节点的重要性。K-核分解法在分析大规模网络的层级结构等方面有很多应用，然而也存在一定的局限性，有很多后续的改进、改良K-壳分解法的研究工作[18]。此外，还有PageRank 算法[19]、LeaderRank算法[20]和HITS算法[21]等。

2网络的鲁棒性指标

网络的鲁棒性是指网络中的一个或多个部件遭到破坏时，网络维持其基本性能的能力。网络的脆弱性是指当网络的结构遭遇变化时，其所遭受的破坏能力，即系统崩溃的可能性。鲁棒性与脆弱性分别从稳定指标与失效指标的角度来表征网络的特性，两者相辅相成。网络的鲁棒性越大，则其脆弱性就越小，即抗毁能力越强。网络的鲁棒性越小，则其脆弱性越大，即其抗毁能力越弱。下面介绍两种常用的鲁棒性指标：

2.1最大连通度Gmax

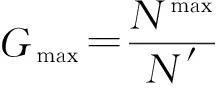
2.2连通因子ϖ

网络的鲁棒性或脆弱性都是从网络的拓扑结构的视角来检验网络的抗毁能力。识别网络中的重要节点有助于梳理网络的拓扑结构，提高对网络的整体把握能力。因而识别网络中的重要结点并加以重点维护或保护，有助于提高网络的鲁棒性。

3实例应用

以图1所示的网络为例，该网络由12个结点构成，其中节点最大的度为4，平均度为1.8333。通过计算得知，节点的度中心DC、介数中心BC、紧密度中心CC及将DC、BC和CC运用证据理论融合后得到的新指标DBC[16]值，如表1中第2～4列所示。

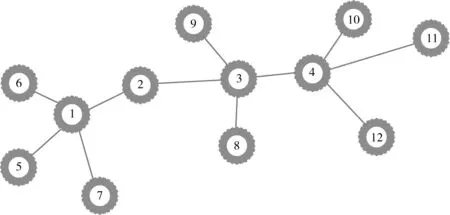
图1　示例网络

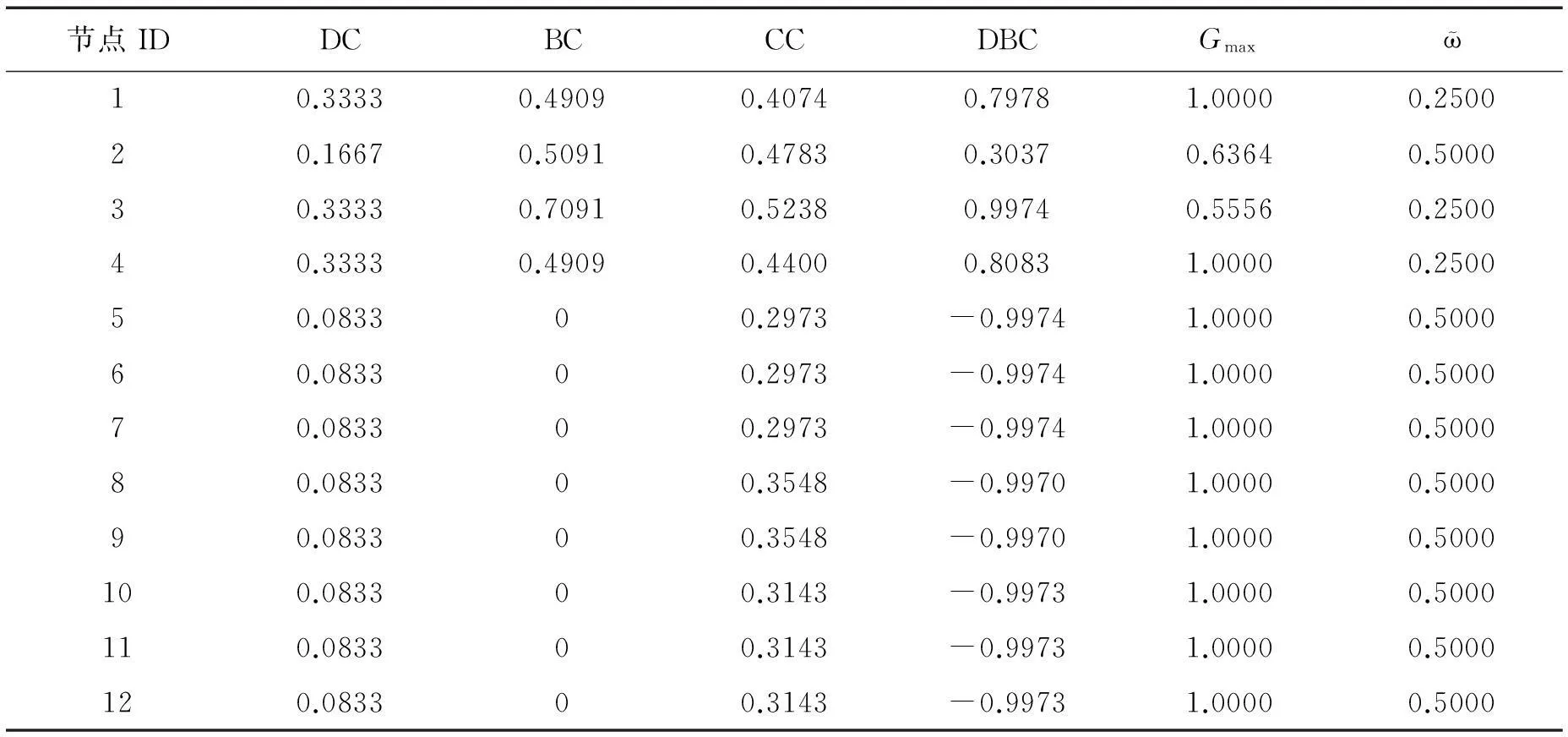
节点IDDCBCCCDBCGmax10.33330.49090.40740.79781.00000.250020.16670.50910.47830.30370.63640.500030.33330.70910.52380.99740.55560.250040.33330.49090.44000.80831.00000.250050.083300.2973-0.99741.00000.500060.083300.2973-0.99741.00000.500070.083300.2973-0.99741.00000.500080.083300.3548-0.99701.00000.500090.083300.3548-0.99701.00000.5000100.083300.3143-0.99731.00000.5000110.083300.3143-0.99731.00000.5000120.083300.3143-0.99731.00000.5000

从表1可知，节点1、节点2、节点3和节点4是上述算法的指标值最高的4个节点。然而，在DC算法中，节点1、节点3和节点4有相同的值因而被认定为同等重要。BC、CC和DBC算法中节点3的值最大，因而节点3被判定为最重要的节点。

当移除网络中的某个节点后，网络的最大连通度及连通因子值变化如表1中第6～7列及图2所示。

图2　节点的最大连通度Gmax与连通因子ϖ

对于该网络，从表1及图2可知，当移除节点3后，网络的Gmax与连通因子值ϖ都达到最小值。结合上述的不同的节点重要度算法可知，节点3为该网络的最重要节点。即当节点3失效后，网络最脆弱，网络的鲁棒性最差。反之，移除一些末梢节点(如节点5、节点12等)后，网络的最大连通度及连通因子都维持在一个较高的值，网络的鲁棒性较好。

4结论

在大数据背景下，网络体系越来越庞大，内部结构越来越复杂，网络的可靠性越来越受到人们的关注。实例验证表明，通过识别网络中的重要节点来探寻网络的鲁棒性是可行的。识别网络中的重要节点，并对其加强维护或保护，有利于提升网络的抗风险能力，提高网络的可靠性。从融合节点的多重属性的角度来挖掘网络中的重要节点来验证网络的鲁棒性是下一步的研究方向。

[参考文献]

[1]彭志莲.智能农业中物联网技术的应用分析[J].长春师范学院学报:自然科学版,2014,33(1):59-60.

[2]于昊.MSTP在辽宁电力传输网中的应用[J].长春师范学院学报:自然科学版,2014,33(6):50-51.

[3]Strogatz S H.Exploring complex networks[J].Nature,2001,410(6825):268-276.

[4]Barabási A L,Albert R.Emergence of scaling in random networks[J].Science,1999,286(5439):509-512.

[5]Callaway D S,Newman M E J, Strogatz S H, et al.Network robustness and fragility: Percolation on random graphs[J]. Physical review letters,2000,85(25):5468.

[6]Min B,Do Yi S,Lee K M,et al.Network robustness of multiplex networks with interlayer degree correlations[J]. Physical Review E,2014,89(4):042811.

[7]Beygelzimer A,Grinstein G,Linsker R,et al.Improving network robustness by edge modification[J].Physica A: Statistical Mechanics and its Applications,2005,357(3):593-612.

[8]Freeman L C.Centrality in social networks conceptual clarification [J].Social networks,1979,1(3):215-239.

[9]Albert R,Jeong H,Barabási A L.Internet:Diameter of the world-wide web[J].Nature,1999,401(6749):130-131.

[10]Freeman L C.A set of measures of centrality based on betweenness[J].Sociometry,1977:35-41.

[11]Du Y,Gao C, Hu Y,et al.A new method of identifying influential nodes in complex networks based on TOPSIS[J]. Physica A:Statistical Mechanics and its Applications,2014,399:57-69.

[12]Wei D,Deng X,Zhang X,et al.Identifying influential nodes in weighted networks based on evidence theory[J]. Physica A:Statistical Mechanics and its Applications,2013,392(10):2564-2575.

[13]Gao C,Wei D,Hu Y,et al.A modified evidential methodology of identifying influential nodes in weighted networks[J].Physica A:Statistical Mechanics and its Applications,2013,392(21):5490-5500.

[14]Dempster A P.Upper and lower probabilities induced by a multivalued mapping[J].The annals of mathematical statistics,1967:325-339.

[15]Shafer G.A mathematical theory of evidence[M].Princeton:Princeton university press,1976.

[16]Mo H,Gao C,Deng Y.Evidential method to identify influential nodes in complex networks[J].Journal of Systems Engineering and Electronics,2015,26(2):381-387.

[17]Kitsak M,Gallos L K,Havlin S,et al.Identification of influential spreaders in complex networks[J].Nature Physics,2010,6(11):888-893.

[18]Wei B Liu J,Wei D,et al.Weighted k-shell decomposition for complex networks based on potential edge weights [J].Physica A:Statistical Mechanics and its Applications,2015,420:277-283.

[19]Page L,Brin S,Motwani R,et al.The pagerank citation ranking: Bringing order to the web[C].Brisbane, Australia,In Proceedings of the 7th International World Wide Web Conference,1998:161-172.

[20]Lü L,Zhang Y C,Yeung C H,et al.Leaders in social networks, the delicious case[J].PloS one,2011,6(6):e21202.

[21]Kleinberg J M.Authoritative sources in a hyperlinked environment[J].Journal of the ACM,1999,46(5):604-632.

[22]罗筱如.基于复杂网络理论的电力网络鲁棒性及脆弱性分析[D].成都:西南交通大学,2012.

An Application of the Nodes Importance in Network Robustness

MO Hong-ming

(Sichuan Minzu College, Kangding Sichuan 626001, China)

Abstract:How to evaluate network robustness is still a hot issue. Identifying the influential nodes and classifying the structure of networks will help to enhance the controllability of networks. In recent years, some progress has been made in the research of identifying the influential nodes. This paper, thereafter, proposes a new method to confirm the robustness of network on the basis of influential nodes in complex networks. The experiments have proved that the more influential the nodes are, the more influence they will have on robustness.

Key words:complex network; influential nodes; robustness; vulnerability

[作者简介]莫泓铭(1983- )，男，助理研究员，西南大学硕士研究生，从事不确定信息处理、复杂网络的节点重要度研究。

[基金项目]四川省教育厅理工科一般科研项目“基于复杂网络节点重要度识别理论的网络鲁棒性研究”(14ZB0322)；国家民委自筹科研项目“基于证据理论的决策方法及其在民族地区生态环境治理决策中的应用”(14SCZ014)。

[收稿日期]2015-12-21

[中图分类号]TP391.9

[文献标识码]A

[文章编号]2095-7602(2016)02-0022-04