基于数值积分的变位储油罐罐容表标定的改进算法
侯国亮,李希瑞,孙 敏,林泳坤
(1.长春师范大学数学学院,吉林长春 130032;2.长春师范大学工程学院,吉林长春 130032)
基于数值积分的变位储油罐罐容表标定的改进算法
侯国亮1,李希瑞2,孙敏2,林泳坤2
(1.长春师范大学数学学院,吉林长春 130032;2.长春师范大学工程学院,吉林长春 130032)
[摘要]本文采用细化积分区域的方法给出了标定变位储油罐罐容表的数值积分新算法,该算法克服了文献[1]中所提算法在油面高度较低时计算误差大的缺点。数值实验表明,本文所提算法正确有效。
[关键词]细化积分区域;数值积分;罐容表;变位储油罐
1问题背景介绍
通常加油站都有若干个储存燃油的地下储油罐,并且一般都有与之相配套的“油位计量管理系统”,采用流量计和油位计来测量进、出油量与罐内油位高度等数据,通过预先标定好的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况.
许多储油罐在使用一段时间后,由于地基变形等原因,就可能会使罐体的位置发生纵向倾斜和横向偏转等变化(以下称之为变位),从而导致罐容表发生改变.按照有关规定,需要定期对罐容表进行重新标定.图1是一种典型的储油罐尺寸及形状示意图,其主体为圆柱体,两端为球冠体,图2是其罐体发生纵向倾斜变位的示意图,图3是罐体发生横向偏转变位的截面示意图.
现阶段,变位储油罐罐容表的标定工作均是由人工或半人工操作实现的.需要在加油站停工条件下进行,而且操作程序繁琐复杂,技术要求严格,时间周期长,这样做既影响加油站的正常运转,也需要较高的经济成本,同时还会有一定的系统误差和测量误差.为此,运用记录的储油罐进、出油量的实际数据,进行建模分析,正确识别罐体变位参数,实时修正罐容表,将是一项非常有现实意义的研究课题.
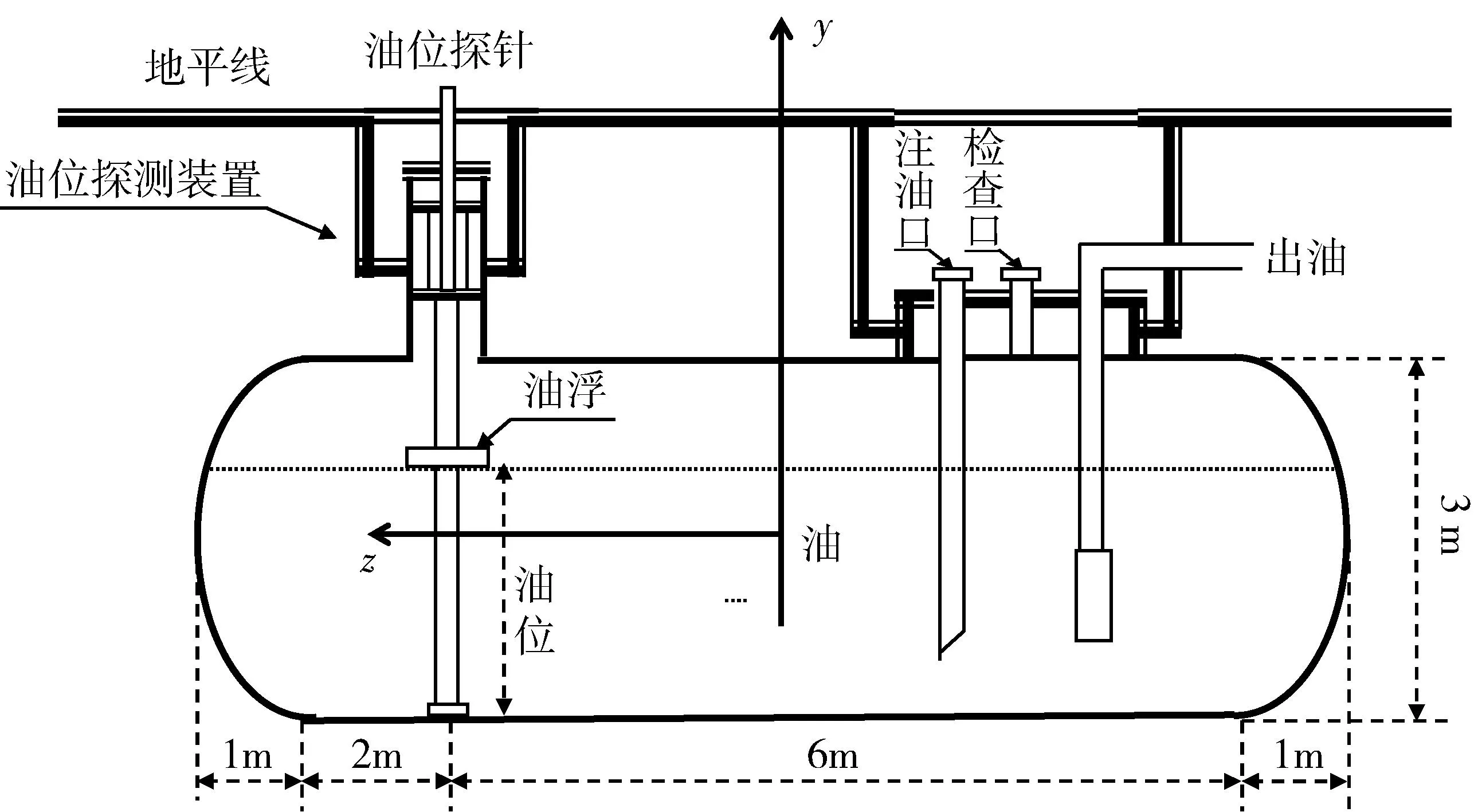
图1 储油罐正面示意图

图3 储油罐截面及坐标系示意图
针对该问题,文献[1]运用坐标旋转变换、示性函数和Matlab中计算重积分的程序来计算任意变位后的罐内油量与油面高度,大大简化了繁琐的数学推导过程①,是解决该问题的一种实用算法,值得推广.但该方法的一个致命缺点是当变位储油罐内油面高度较低时计算的罐内油量与油面高度相对应的数据误差较大,因此如何克服此缺点就成了此方法是否能得到广泛推广应用的一个关键性问题.本文在深入分析该法的计算程序基础之上,采用细化积分区域的方法,提出了此法的改进算法程序,成功地克服了该致命缺点.数值实验表明,新算法正确有效,为该类方法的实际推广应用奠定了扎实的基础.
2算法的理论分析
2.1坐标系的建立
建立固连于油罐并随油罐一起转动的空间直角坐标系,以油罐中心为坐标原点,中央横截面为xOy平面,x轴、y轴的正方向如图3(a)所示,z轴正方向由右手定则确定,即沿中轴线方向,如图1所示. 规定,如无特别说明,下文中涉及的区域及其约束条件的数学表达式均是在此坐标系下得到的.
2.2积分区域的确定
依据多重积分的几何意义可知,对罐内油量所占据的空间区域进行积分即可得到油的体积.该问题中所涉及的积分区域受两类条件约束,一是油罐外壳的约束,二是油面所在平面的约束.其中,油罐外壳约束可表述为

其中,r=1.5m,R表示油罐两端的球冠所在的球面半径,S表示坐标原点到球冠所在的球面球心的距离.下面讨论储油罐发生变位后油面所在平面的数学表达式.为了叙述的方便,规定储油罐发生纵、横向变位时的两个转角按逆时针转动时为正,如图4所示.

图4 转角示意图
根据相对运动的思想,当储油罐绕x轴转动α角、绕z轴转动角β时,我们可以设想成储油罐未动,而是罐内实际油面所在的平面以油浮子所在位置(0,h-r,2)为定点,绕x轴转动了-α角,绕z轴转动了-β角,其中h表示储油罐“油位计量管理系统”显示的油位高度.这种等效转化的思想能在不影响体积计算的前提下,使得关于积分区域约束条件的讨论大幅简化.接下来,本文就运用这种思想给出油面所在的平面以油浮子所在位置(0,h-r,2)为定点,绕x轴转动-α角、绕z轴转动-β角后所得对应平面的数学表达式.
首先,由坐标变换相关知识可求出绕x轴转动-α角,绕z轴转动-β角的变换矩阵.设变换前点的坐标为(ξ,η,ζ),变换后点的坐标为(x,y,z),则绕x轴转动-α角的变换可表述为

绕z轴转动-β角的变换为

一般来说,绕定点转动物体的有限角位移具有不可交换性,但由于该问题中所涉及的转动角α、β均很小,以至于变位次序对变位后的结果几乎没有影响,所以,旋转前的点(ξ,η,ζ)与旋转后的点(x,y,z)之间的关系可表示为

或T=T2T1均可.按T=T1T2展开得
η=xcosαsinβ+ycosαcosβ-zsinα.
代入η=0即可得由xOz坐标平面绕x轴旋转-α角,并再绕z轴旋转-β角后所得对应平面的数学表达式为
Γ:xcosαsinβ+ycosαcosβ-zsinα=0.
其次,若把此时罐内油面所在的平面按照上述要求旋转后的平面记为平面Η,则平面Η与平面Γ平行,区别在于平面Η经过油浮子所在的位置,即油浮子所表示的点在平面Η上,所以平面Η的方程可表述为
xcosαsinβ+ycosαcosβ-zsinα=C.
其中,C为一常数.若将油浮子坐标(0,h-r,2)代入,即可得
C=(h-r)cosαcosβ-2sinα.
所以按要求转动后油面所在的平面方程为
Η:xcosαsinβ+ycosαcosβ-zsinα=(h-r)cosαcosβ-2sinα.
而油总是位于平面Η的下面,所以积分区域可表示为

3数值实验
在该部分,我们主要运用Matlab函数triplequad给出基于积分区域

的标定变位储油罐罐容表的数值积分算法程序.
若定义关于积分区域D的示性函数为

则储油罐内油的体积V(m3)与旋转角度α、β及储油罐“油位计量管理系统”显示的油位高度h(m)之间的关系可表示为

其中,积分区域E为能包含区域D的最小区域.
文献[1]中的标定变位储油罐罐容表的数值积分算法就是根据上述理论提出的,该方法避开了传统积分方法对积分上下限的繁琐讨论(参见文献[7]).当变位储油罐内油面较高时,用该算法标定变位储油罐罐容表误差小、精度高;但当变位储油罐内油面较低时,用该方法标定变位储油罐罐容表误差大,具体情况详见表1中相对应的数值结果.本文通过细化积分区域的途径,给出了基于上述理论的标定变位储油罐罐容表的数值积分新算法,该算法是文献[1]中所提算法的改进,能够很好地克服原算法的不足,相关的数值表现如表1所示.

表1 相关算法的部分数值实验数据

横向续表

横向续表

横向续表
注:表1中第一行所列数据是变位储油罐自带系统显示的油位高度,单位为m;第二行的所有数据是根据文献[7]中所给方法编程(qingxie200.m)算出的变位储油罐内不同油位高度时对应的油量容积,单位是m2,因该方法是用繁琐的传统积分方法得到的,故所得的数据可作为用以衡量其它方法好与劣的标准数据指标;第三行所列数据是运用文献[1]中所提的数值积分算法编程(qingxie210.m)计算的;而第四行里的所有数据是用本文所给的数值积分改进算法编程(qingxie211.m)算出的.
从表1所列数据不难看出,当变位储油罐内油量较少时,即罐内油位高度很低时,用文献[1]中所给的数值积分算法标定变位储油罐罐容表时误差大,而用本文所提的数值积分改进算法可以很好地解决该问题.当然,对于变位储油罐内油量很足时,即罐内油位高度不低时,这两个方法均能对变位储油罐罐容表进行很好的修正.
文中所涉及的主要算法的实现程序码:
qingxie211.m
r=1.5;R=1.625;s=5-R;a=(2.11*pi)/180; b=(4.31*pi)/180; ta=sin(a)/cos(a); ct=cos(a)/sin(a); h=zeros(1,31); V=zeros(1,31);
for i=1:31
h(i)=0.1*(i-1);
if h(i)<=6*ta
zc=2-h(i)*ct*cos(b); bd=(5-zc)*ta-r;
V(i)=triplequad(@(x,y,z)(x*cos(a)*sin(b)+y*cos(a)*cos(b)-z*sin(a)<=cos(a)*cos(b)*(h(i)-r)-2*sin(a)).*(x.^2+y.^2<=r^2).*(z>=-s-sqrt(R^2-x.^2-y.^2)).*(z<=s+sqrt(R^2-x.^2-y.^2)),-r,r,-r,bd,zc,5);
elseif h(i)<=1.5-3*ta
be=h(i)+3*ta-1.5;
V(i)=triplequad(@(x,y,z)(x*cos(a)*sin(b)+y*cos(a)*cos(b)-z*sin(a)<=cos(a)*cos(b)*(h(i)-r)-2*sin(a)).*(x.^2+y.^2<=r^2).*(z>=-s-sqrt(R^2-x.^2-y.^2)).*(z<=s+sqrt(R^2-x.^2-y.^2)),-r,r,-r,be,-5,5);
else
V(i)=triplequad(@(x,y,z)(x*cos(a)*sin(b)+y*cos(a)*cos(b)-z*sin(a)<=cos(a)*cos(b)*(h(i)-r)-2*sin(a)).*(x.^2+y.^2<=r^2).*(z>=-s-sqrt(R^2-x.^2-y.^2)).*(z<=s+sqrt(R^2-x.^2-y.^2)),-r,r,-r,r,-5,5);
end
end V
qingxie210.m
r=1.5;R=1.625;s=5-R;a=(2.11*pi)/180; b=(4.31*pi)/180;
h=zeros(1,31); V=zeros(1,31);
for i=1:31
h(i)=0.1*(i-1);
V(i)=triplequad(@(x,y,z)(x*cos(a)*sin(b)+y*cos(a)*cos(b)-z*sin(a)<=cos(a)*cos(b)*(h(i)-r)-2*sin(a)).*(x.^2+y.^2<=r^2).*(z>=-s-sqrt(R^2-x.^2-y.^2)).*(z<=s+sqrt(R^2-x.^2-y.^2)),-r,r,-r,r,-5,5);
end V
qingxie200.m
r=1.5; R=1.625; a=(2.11*pi)/180; b=(4.31*pi)/180; si=sin(a);cs=cos(a);
ta=si/cs;ct=cs/si; h=zeros(1,31); V=zeros(1,31);
for m=1:31
h(m)=0.1*(m-1); H=(h(m)-r)*cos(b)-2*ta;
if H<=(4*ta-r)
xA=3.375*si*cs+H*cs^2+si*sqrt(R^2-(3.375*si+H*cs)^2);
xB=H+4*ta; V1=quad(@g3,xB,xA,[],[],H,ct); V2=quad(@g4,-1.5,xB);
V(m)=2*quad(@g1,xB,xA,[],[],H,ct)+2*quad(@g2,-1.5,xB,[],[],H,ct)+2*V1+2*V2;
else
xA=3.375*si*cs+H*cs^2+si*sqrt(R^2+(3.375*si+H*cs)^2); xB=H+4*ta; xC=H-4*ta; xD=-3.375*si*cs+H*cs^2+si*sqrt(R^2-(3.375*si-H*cs)^2);
V3=quad(@f2,xB,xA,[],[],H,ct); V4=quad(@g4,xC,xB);
V5=quad(@g4,-1.5,xC); V6=quad(@f3,xD,xC,[],[],H,ct);
V(m)=2*quad(@g1,xB,xA,[],[],H,ct)+2*quad(@g2,xC,xB,[],[],H,ct)+13.5*
quad(@f4,-1.5,xC)-2*quad(@f1,xD,xC,[],[],H,ct)+2*V3+2*V4+4*V5-2*V6;
end end
for n=1:31 V(n)=real(V(n)); end V
function y=f1(x,H,ct) %以下8个函数为程序qingxie200.m中的调用函数
y=((x-H)*ct+3.375).*sqrt(1.625^2-x.^2-((H-x)*ct-3.375).^2);
function y=f2(x,H,ct)
y=0.5*sqrt(1.625^2-x.^2-((H-x)*ct+3.375).^2).*sqrt(((H-x)*ct+3.375).^2)+0.5*(1.625^2-x.^2).*asin(sqrt((1.625^2-x.^2-((H-x)*ct+3.375).^2)./(1.625^2-x.^2)));
function y=f3(x,H,ct)
y=0.5*sqrt(1.625^2-x.^2-((H-x)*ct-3.375).^2).*sqrt(((H-x)*ct-3.375).^2)+0.5*(1.625^2-x.^2).*asin(sqrt((1.625^2-x.^2-((H-x)*ct-3.375).^2)./(1.625^2-x.^2)));
function y=f4(x) y=sqrt(2.25-x.^2);
function y=g1(x,H,ct)
y=((H-x)*ct+3.375).*sqrt(1.625^2-x.^2-((H-x)*ct+3.375).^2);
function y=g2(x,H,ct) y=((H-x)*ct+3.375).*sqrt(2.25-x.^2);
function y=g3(x,H,ct)
y=0.5*sqrt(1.625^2-x.^2-((H-x)*ct+3.375).^2).*sqrt(((H-x)*ct+3.375).^2)+0.5*(1.625^2-x.^2).*asin(sqrt((1.625^2-x.^2-((H-x)*ct+3.375).^2)./(1.625^2-x.^2)));
function y=g4(x)
y=0.5*sqrt(2.25-x.^2).*sqrt(1.625^2-2.25)+0.5*(1.625^2-x.^2).*asin(sqrt((2.25-x.^2)./(1.625^2-x.^2)));
[注 释]
①文献[7]中所提的解决方法即是用繁琐的多元微积分知识获得的,但此法的计算精度高,稳定性、通用性好。本文数值实验部分的标准数据即是用该方法编程计算得到的。
[参考文献]
[1]姜亚中,淡志强,吕晓帆,等.基于数值积分的储油罐的变位识别与罐容表标定[J].工程数学学报,2010,27(Supp.1): 39-46.
[2]姜启源,谢金星,叶俊.数学建模[M].3版.北京:高等教育出版社,2003.
[3]韩中庚.数学建模方法及其应用[M].2版.北京:高等教育出版社,2009.
[4]刘仁云,张晓丽,侯国亮.数学建模方法与数学实验[M].北京:中国水利水电出版社,2011.
[5]同济大学数学系.高等数学(下册)[M].7版.北京:高等教育出版社,2014.
[6]苏金明,阮沈勇.MATLAB实用教程[M].北京:电子工业出版社,2005.
[7]韩中庚,杜剑平.储油罐的变位识别与罐容表标定模型[J].工程数学学报,2010,27(Supp.1):92-102.
Improved Algorithm of Calibration of Capacity Table of Oil Tank of Deflection Based on Numerical Integration
HOU Guo-liang1, LI Xi-rui2, SUN Min2, LIN Yong-kun2
(1.School of Mathematics, Changchun Normal University, Changchun Jilin 130032, China;2.School of Mechanical Engineering, Changchun Normal University, Changchun Jilin 130032, China)
Abstract:In this paper, using the approach of subdividing domain of integration a new algorithm of Calibration of Capacity Table of oil tank of deflection is proposed. This new algorithm is based on numerical integration and overcomes the drawback of the large error of calculation that arises from the algorithm’s applications presented in the literature [1]. Preliminary numerical results indicate that the method given in this paper is correct and efficient.
Key words:subdividing domain of integration; numerical integration; capacity table of oil tanks;oil tank of deflection
[作者简介]侯国亮(1981- ),男,讲师,博士研究生,从事计算数学可信验证、数值代数研究。
[基金项目]国家级大学生创新创业训练计划项目“建模分析储油罐的变位识别与罐容表标定”(201410205020)。
[收稿日期]2015-11-17
[中图分类号]O151;O24
[文献标识码]A
[文章编号]2095-7602(2016)02-0001-06

