振动台子结构试验方法实现的韧性防灾需求与其关键问题

唐贞云 洪越 李振宝

摘要：振动台子结构试验可解决振动台试验中缩尺比例过小、结构构造措施难以准确模拟、非结构构件动力响应难以研究等问题。基于振动台子结构试验应用于结构韧性防灾中存在的潜在需求，探讨了振动台子结构试验原理及其实现的关键技术问题。研究结果表明：振动台子结构试验以数值仿真与物理试验相结合的方式间接增加振动台试验能力，具有增大物理试验尺寸、减小尺寸效应影响的优点。但是在数值子结构计算效率、试验系统稳定性分析、物理加载精度、数值子结构建模精度和边界条件模型等方面还需要进一步开展系统的研究。

关键词：振动台;实时子结构试验;结构韧性;数值积分;稳定性;系统控制

0 引言

21世纪，人类多次面临大震下整个城市瘫痪，重建难度大、时间长的问题，工程结构的抗震设防目标不再局限于“小震不坏、中震可修、大震不倒”，而是对包括结构、非结构系统的震后功能恢复提出了新的要求。基于此，众多学者提出韧性城市（杨静等，2019;陆新征等，2017）的概念，其具体内涵包括：小震时城市可以快速恢复;大震时城市几个月内基本恢复正常运行等。城市抗震韧性是指采用多种措施来增强城市防震减灾的能力，在遇到突发地震后，城市功能和社会经济发展能快速恢复，主要包括重要公共设施如医院、核电站等建筑要具备震中使用功能不受损失的能力，学校、行政机关等要具备震后快速恢复的能力，道路桥梁、水电管网等城市基础设施要有震后及时恢复能力，避免阻碍救援或形成二次灾害等现象。

为了配合地震工程研究的需求，近年来发展起来一些抗震试验技术（谢礼立，马玉宏，2003），主要有：拟静力试验、拟动力试验、振动台试验和混合试验。拟静力试验（赵均等，2014）主要通过施加逐步增大的低周往复位移或力时程，模拟试件从弹性到破坏全过程的恢复力特性，但在试验中加载历程需人为预先设定，与地震作用下结构的实际位移时程相关性较小。为了解决这一问题，出现了拟动力试验（侯杰等，2006），主要通过求解动力方程得到在地震作用下结构的真实位移时程，然后再施加于试件。振动台可以再现地震动，较好地弥补了静力加载抗震试验的不足，但振动台的建设尺寸和加载能力限制了试件尺寸。因此，实时子结构试验（Nakashima et al，1992，2020）被提出，按加载设备不同，实时子结构试验包括基于作动器（郭珺等，2017）、振动台（高春华等，2014）和二者同时使用（Shao et al，2011）3类。

提高工程结构抗震韧性是确保实现韧性城市的关键，装配式建筑作为目前广泛采用的结构建造形式，常与减隔震设计配合使用。采用振动台进行试验时，减隔震设计下的装配式结构中的节点连接、构造措施以及结构内部的非结构构件和设备用具等均无法通过大比例缩尺模型模拟，且对于需要考虑土、波浪等介质影响的工程结构需要模拟的空间尺寸更大，缩尺模型试验的可靠性更低。鉴于此，本文主要讨论采用振动台加载、振动台和作动器共同加载的实时子结构试验，此处统称为振动台子结构试验，从韧性防灾需求、振动台子结构试验原理、振动台子结构试验实现关键问题3方面进行探讨。

1 振动台子结构试验韧性防灾需求1.1 减隔震结构动力响应试验研究

减隔震结构主要包括隔震、减震（被动、半主动和主动减震）两种形式。隔震结构通过在结构与大地之间或者结构不同层之间设置隔震层，以减小地震作用向上传播（Asai et al，2015）。隔震装置（如橡胶垫或摩擦摆）是实现隔震的最关键环节，为了达到隔震目的，必须具备以下功能：较小的水平刚度和足够大的竖向承载力。用传统振动台试验研究隔震结构的整体动力响应时，需要同时对隔震层和隔震结构进行大比例缩尺，因此，在隔震层性能模拟方面存在以下不足：①大比例缩尺使得隔震层在尺寸和材料使用上与原结构均发生变化，比如小尺寸橡胶垫中钢板与橡胶比例、摩擦摆的摩擦层等均无法按比例加工，从而使隔震装置存在尺寸效应;②所有大比例缩尺振动台试验模型几乎均处于欠质量状态，使隔震层承受竖向压力不足，水平刚度偏小，无法准确描述隔震层对上部结构的隔震效果。针对上述问题，可采用圖1所示的2个阶段子结构试验：第一阶段，通过足尺试验对隔震层的力学行为进行试验测试，再建立准确数值模型，避免尺寸效应;第二阶段：基于所建立的数值模型，把隔震层作为数值子结构进行数值模拟，上部结构作为物理子结构进行试验测试，可解决上部结构缩尺带来的竖向压力不足的问题，从而降低竖向压力不足对水平刚度的影响。

对于高层和超高层建筑，为了控制结构上部动力响应，通常在合适位置设置质量调谐减震装置（被动、半主动和主动），如质量调谐阻尼器（Tuned Mass Damper，TMD）、液体调谐阻尼器（Tuned Liquid Damper，TLD）（Lee et al，2007）、主动质量阻尼器（Active Mass Damper，AMD）等。被动减震装置中阻尼的非线性较强，半主动装置中阻尼项是地震作用的时变函数，主动装置中调谐装置的出力随地震作用而自适应变化。因此，对这类装置进行试验研究时，重点在于对减震装置性能的模拟。采用传统振动台试验时，需要对减震装置和结构进行整体模拟，大比例缩尺会使几十吨出力的大装置变成了几公斤出力的微型装置，特别是缩尺后的阻尼器难以加工，更无法保障其力学性能的准确性，同时，对地震输入时程进行大比例压缩，地震输入频率大比例提高，这相当于人为放大输入地震动的速度，而阻尼器的出力与速度密切相关，所以试验中阻尼特性的模拟与其实际特性相差较大。而图1所示的两阶段振动台子结构试验可以在保证对减震装置特性进行准确模拟的前提下，对结构减震性能进行整体模拟，从而避免了大比例缩尺对减震装置、结构动力性能的不利影响，可较好地模拟减震装置对风或地震作用下结构破坏全过程的影响。

1.2 多介质耦合下结构动力响应试验研究

工程结构主要建造在陆地上或者江河湖海中，结构所受的全部荷载都需要通过基础传递到土体或液体介质中。因此，在风、海啸、地震等作用下，结构的韧性防灾能力不但和结构性能和外荷载特性相关，也和结构与土体、液体等介质的耦合作用密切相关。土-结构相互作用（李振宝等，2010;姜忻良等，2019）是工程结构研究的经典问题，主要包括3个方面：结构建在硬土上，可视为固定约束忽略土体的影响;低矮结构建在软土上，可视为具有减震效果，作为结构安全储备不做特别考虑;高层、高耸、桥梁等柔性结构建在软土上，结构周期与场地特征周期相近，需要重点考虑。隔震技术通过延长结构周期减小结构响应，但在软土上进行短周期结构建设时，会面临与柔性结构一样的问题，需要考虑土-结构相互作用。对这类土-结相互作用系统进行振动台试验研究时，需要将结构和承载结构的土体均作为物理模型。由于需要模拟土体边界的影响，土体的重量和尺寸比结构还要大，所以其试验模型比纯粹的结构振动台试验模型更小。目前在这样的试验能力下，考虑土体影响的结构动力响应试验研究基本处于定性阶段，离定量化研究还有一定距离。结构韧性防灾能力研究对土-结构相互作用试验量化研究提出了新的要求。

多介质耦合除了土体的影响外还有液体与结构相互作用，如跨河/跨江大桥、海上风电、海洋平台、隔震/非隔震储液罐等结构在遭受地震、海啸时，其动力响应的影响不仅会受土体性能的影响，波浪荷载对其结构的作用也不可忽略。目前对波浪荷载的试验模拟主要采用造波机，对地震和波浪的耦合作用试验模拟主要通过造波机和振动台联合模拟，如天津大学和河海大学建成了相关试验设备，但目前具备这个试验能力的单位还较少，且试验试件同样受振动台尺寸及加载能力的限制，大比例缩尺仍然不可避免。

为了解决土与结构动力相互作用、波浪与结构动力作用以及二者的耦合相互作用试验研究需求，可将图1所示策略扩展为多阶段子结构试验，分别开展试验研究，再通过子结构试验技术将多因素耦合研究整个系统的动力特性。例如，通过大尺寸试验研究土-基础阻抗函数、波浪荷载规律，而后将土体、波浪均作为数值子结构，工程结构进行物理试验，采用振动台和作动器分别进行地震作用和波浪作用的加载模拟，从而达到整体系统大尺寸试验研究的目的。

1.3 非结构系统地震响应规律试验研究

建设建筑结构的目的在于其功能需求，非结构系统的投资远高于主体建筑的投资。震害表明，造成非结构构件损害的地震强度更低，同级别地震作用下非结构构件损坏更严重（贺思维等，2017）。因此，研究非结构系统中各类构件的抗震性能是韧性研究的重要环节。研究需求主要包括填充墙、吊顶、幕墙、管道、医疗设备等。根据受力特性的不同，非结构构件可以分为位移影响型和加速度影响型，通常分别采用拟静力试验和动力试验方法试验其抗震性能。非结构系统安装在结构中的不同位置，其动力特性不但与地震动相关，与结构自身动力特性也密切相关。因此，直接决定其动力响应的是非结构系统所在位置的时程响应。与主体结构相比，其质量可以忽略不计，且主体结构方便建立数值计算模型时，在动力试验中通常只需对非结构系统及其连接件进行模拟，将数值计算所得非结构系统所在位置的响应作为输入进行试验。当非结构系统质量不可忽略而需要考虑其与主体结构之间相互作用，或者主体结构本身也需要进行试验研究时，大比例缩尺振动台试验将再次面临挑战。振动台子结构试验有可能为解决该问题提供途径，可以将无法缩尺的非结构系统（构件或设备）作为物理子结构进行试验研究，将主体结构部分作为数值子结构进行仿真或者并行物理子结构试验，从而对两者相互作用加以考虑，再现非结构系统在地震中的真实响应。

2 振动台子结构试验原理

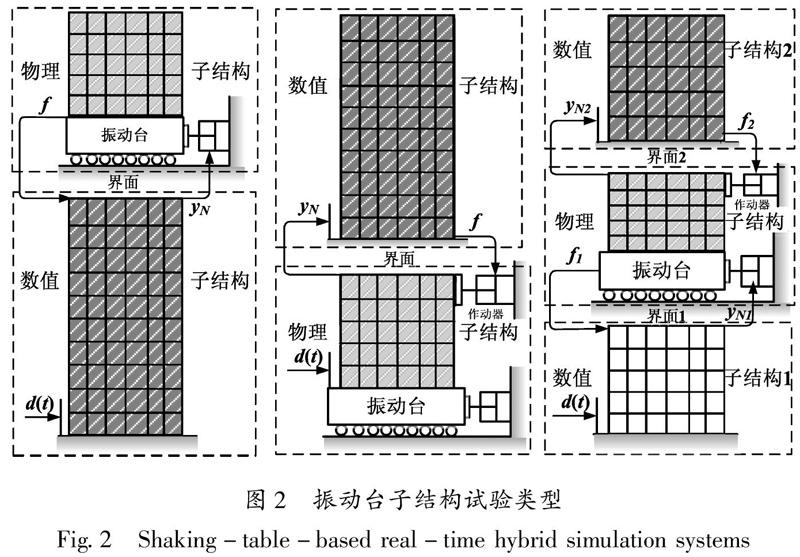
子结构试验的优势在于可以将研究对象按建模难易程度分为数值模拟和物理测试两部分，还能保持结构的完整动力特性。在试验设备能力不变的情况下，试验测试部分的尺寸可以大幅度增大，从而避免大比例缩尺带来的试验误差。依据韧性防灾需求，振动台子结构试验大体可以分为如图2所示的3种情况：第一种：上部结构非线性更强，可作为物理子结构进行试验，下部结构进行数值仿真，如新型TMD/TLD减震装置研究、液体储罐隔震等。另外，土-结构动力相互作用系统研究过程中重点关注上部结构动力响应时也可采用该方式。第二种：下部结构非线性更强，作为物理子结构进行试验测试，上部结构作为数值子结构，如高层结构的破坏主要集中在底部阶层而上面部分基本处于弹性阶段，或者土-结构动力相互作用系统中重点关注土-基础系统特性。第三种：重点关注结构中间部分，将其作为物理子结构，其余部分结构作为数值子结构，如有转换层或中间薄弱层的结构等。

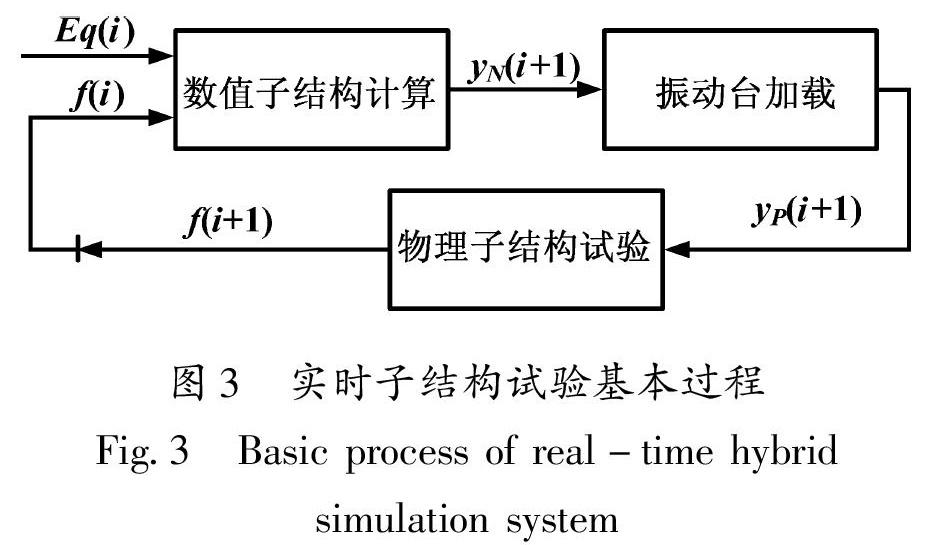
从子结构试验实现角度，图2所示的3类振动台子结构试验可以分为两类：前两种试验系统只有一个数值与物理子结构界面，所以用振动台或作动器实现界面的物理与数值交互，第二种子结构中所用振动台的作用和传统试验一样，只需再现地震动输入，不需要与数值子结构实时交互;第三种试验系统有多个数值与物理子结构界面，需要多个振动台或作动器与数值子结构进行实时数据交互。由此可知，实时子结构试验的实现过程实际上是保证试验系统中每个数值与物理子结构实时数据交互过程，其交互流程如图3所示，图中Eq代表外荷载，yN是数值子结构计算得到的界面响应，yP为通过加载系统实际加载到物理子结构上的界面响应，f为物理子结构反馈给数值子结构的界面反力。实时子结构试验实现过程为：通过积分算法求解数值子结构在外荷载和物理子结构反作用下的界面响应，将数值子结构与物理子结构之间的界面响应作为指令传输给加载系统（振动台或作动器），在加载系统的作用下物理子结构发生运动，物理子结构再响应反馈给数值子结构，进行下一步试验，所有环节组合成了一个闭环，如此循环往复完成试验。

3 振动台子结构实现关键问题

从图3可知，振动台子结构实现的关键是准确的数值求解和物理加载，以及通过数值和物理模型准确模拟界面边界条件以保证被测试结构的整体特性，而闭环的稳定性是试验成功的前提。

3.1 数值子结构求解

数值子结构的求解实际上就是通过求解结构动力方程得到其数值响应（位移、速度和加速度）。对于复杂的工程结构，特别是考虑非线性特性的结构，动力方程本身非常复杂，同时，地震、风、海啸等灾害荷载多为随机时程，都无法进行严谨的数学表达，这使工程结构动力响应只能采用数值积分算法求得其数值解。为了控制数值解与精确解之间的误差，通常采用小步长显式积分算法（Wu et al，2015）或隐式迭代算法（Newmark，1959）。对于实时子结构试验，隐式迭代算法的计算效率和实时性都无法满足要求，故常用显式积分算法。除计算精度外，积分算法稳定性也是制约子结构试验发展的瓶颈之一，为了满足试验需求，研究人员发展了一批无条件稳定算法（Chang et al，2011;Chen，Ricles，2010;Kolay，Ricles，2014;Gui et al，2014）。结构的时程响应包括位移、速度和加速度，且分别在结构低频、中频和高频响应中占主要成分。目前数值积分算法多以位移显式，速度、加速度隐式为主，故而用位移作为控制量实现试验。对于速度相关型或者高频特性模拟，需要开发更多高效的速度、加速度显式积分算法。目前实现的实时子结构试验中数值子结构的自由度数大多在100以内，尽管学者们在高效率数值积分算法方面做了大量工作，但仍無法满足工程结构研究需求。近年来运用图形处理器（GPU）强大的并行计算能力提高土木工程结构数值计算效率的研究得到了快速发展，其计算效率相比于中央处理器（CPU）最高可达百倍以上（吴恩华，2014;Lu et al，2014;解琳琳等，2014;曹胜涛等，2019），可提高数值子结构计算效率、扩大数值子结构计算规模。

3.2 稳定性研究

数值积分算法、作动器/振动台加载等环节都存在不同程度的误差，当系统为开环时上述误差不会累积。但实时子结构试验相当于给试验系统增加了额外的闭环（图3），导致数值求解和物理加载误差会累积、放大甚至发散，这就是实时子结构试验系统的失稳问题。影响试验系统稳定性的因素为数值/物理子结构动力特性、数值积分算法、加载系统动力特性等，其中加载系统动力特性造成的误差占比更大。对于幅值误差可以忽略的作动器，通常认为其实际和期望响应之间存在时间差，即采用时滞描述其动力特性。为此，学者们针对不同子结构试验系统提出了能量平衡方法（Horiuchi et al，1999）、谱半径法（Wu et al，2009）、时滞差分法（Wallace，2005）、离散根轨迹法（Zhu et al，2015）等。这些方法将加载系统动力特性看作时滞模型，这其中暗含了2个假设（Tang et al，2018）：幅值误差可以忽略，相位与加载频率成正比。图4给出了振动台和作动器动力特性的实际对比，可以看到单作动器在较宽的频带（15 Hz以内）可以满足时滞模型假设条件，但振动台自身质量大，降低了其共振频率，使幅值和相位均只在很小的频率范围（5 Hz以内），满足时滞模型假设。为了准确预测振动台子结构试验系统稳定性，需要采用更复杂的动力模型，比如多阶传递函数。

实时子结构试验系统稳定性预测还存在以下问题：①数值或物理子结构模型多以单自由度为主，无法考虑高阶模态的耦合影响;②进行结构试验的原因在于被测试对象存在无法准确用数学描述的非线性，目前的预测方法多以线性特性为主;③子结构试验系统中数值求解为离散系统，物理加载为连续系统（图3），为了保证计算效率数值求解步长大于物理加载，为了协调加载需要指令插值，但目前的稳定性分析方法对数值和物理子结构均采用连续或离散模型，无法准确描述真实试验系统特性。

3.3 加载系统控制

加载系统控制器设计也通常将加载系统假设为时滞模型。据此发展了时滞补偿控制器，通过将控制指令向外插值预测的方法实现对时滞的补偿。由图4可知，时滞补偿对作动器控制在一定频带是有效的，但对振动台的适用频带太低，无法满足试验研究。受制于振动台尺寸和加载能力，即使用子结构试验也不可避免缩尺，进而会加大对高频性能的需求。韧性防灾需要考虑非结构系统性能，以加速度控制的非结构系统不能忽略结构的高阶响应，也对振动台高频提出了进一步要求。大尺寸试件与振动台的相互作用也会对子结构试验系统产生影响（郭珺等，2016）。因此，一些学者从控制理论出发，将加载系统和物理子结构统一作为控制对象，运用逆传函动力补偿（Wallace，2005）和自适应控制（Stoten et al，2009）对加载系统的时滞和幅值一同进行控制。但目前振动台子结构试验在试验研究中还是以小尺寸试件、低频位移控制为主。对通过加速度进行高频信号控制、振动台与作动器联合实现多物理边界的子结构试验系统中的协同控制、考虑振动台/试件非线性特性实时变化的自适应控制器等均需要进一步的研究。

4 结论

装配式结构的快速发展和韧性防灾需求的提出将会加速减隔震结构的发展应用，同时增大了非结构系统的研究需求，因此对减小大比例缩尺试验局限、增强大尺寸试件试验研究能力提出了新要求。振动台子结构试验以数值仿真与物理试验相结合的方式间接增加振动台试验能力，具有增大物理试验尺寸、减小尺寸效应影响的可能性。为了成功实现振动台子结构试验，在通过数值积分算法研发和高性能硬件应用提高数值子结构计算效率、实时子结构试验系统稳定性综合分析方法、通过高性能控制算法开发提高物理加载精度、通过模型更新提高数值子结构建模精度和边界条件模型等方面，还需要开展进一步系统的研究。

参考文献：

曹胜涛，路德春，杜修力，等.2019.基于GPU并行计算的地下结构非线性动力分析软件平台开发[J].工程力学，36（2）：53-65.

高春华，纪金豹，闫维明，等.2014.地震模拟振动台技术在中国的发展[J].土木工程学报，47（8）：9-19.

郭珺，唐贞云，陈适才，等.2016.试件-加载系统相互作用对实时子结构试验系统稳定性影响[J].工程力学，33（11）：59-67.

郭珺，唐贞云，李易，等.2017.基于子结构试验的土-结相互作用实现研究[J].工程力学，34（S1）：214-219.

贺思维，曲哲，周惠蒙，等.2017.非结构构件抗震性能试验方法综述[J].土木工程学报，50（9）：16-27.

侯杰，刘钧，杜文博，等.2006.框架结构拟动力试验方法研究[J].工程抗震与加固改造，28（6）：66-70.

姜忻良，张崇祥，姜南，等.2019.设备-结构动力相互作用振动台试验方法研究[J].振动与冲击，38（3）：108-115.

解琳琳，韩博，许镇，等.2014.基于OpenSees的大型结构分析GPU高性能计算方法[J].土木建筑工程信息技术，6（5）：22-25.

李振宝，李晓亮，唐贞云，等.2010.土-结构动力相互作用的振动台试验研究综述[J].震灾防御技术，5（4）：439-450.

陆新征，曾翔，许镇，等.2017.建设地震韧性城市所面临的挑战[J].城市与减灾，（4）：33-38.

吴恩华.2004.图形处理器用于通用计算的技术、现状及其挑战[J].软件学报，15（10）：1493-1504.

谢礼立，马玉宏.2003.现代抗震设计理论的发展过程[J].国际地震動态，（10）：1-8.

杨静，李大鹏，翟长海，等.2019.城市抗震韧性的研究现状及关键科学问题[J].中国科学基金，33（5）：525-532.

赵均，侯鹏程，刘敏，等.2014.混凝土框架楼梯结构抗震性能拟静力试验研究[J].建筑结构学报，35（12）：44-50.