基于对称麦克风基阵的枪声定位算法研究

党存禄, 于光祖, 郭永吉

(1. 兰州理工大学 电气工程与信息工程学院， 甘肃 兰州 730050；

2. 甘肃省工业过程先进控制重点实验室， 甘肃 兰州 730050)



基于对称麦克风基阵的枪声定位算法研究

党存禄1,2, 于光祖1,2, 郭永吉1,2

(1. 兰州理工大学 电气工程与信息工程学院， 甘肃 兰州 730050；

2. 甘肃省工业过程先进控制重点实验室， 甘肃 兰州 730050)

摘要:为改善枪声定位系统的性能， 本文提出了双麦克风基阵对称布局的方法. 以7个麦克风构成上下对称的两个正四棱锥基阵， 分别对距离、 俯仰角和方位角公式进行了推导， 搭建物理模型对定距、 定向误差进行仿真分析， 并对双基阵俯仰角的误差进行分析和数据融合. 研究表明所提出的基阵模型对枪声定位系统的定向性能改善较为明显， 可应用于固定监测点或低速车载系统， 能够实现对近距离目标的定位和远距离目标的精确定向.

关键词:枪声定位； 对称基阵； 误差分析； 定向； 定距

0引言

声学定位技术在军事领域有着广泛的应用， 枪声定位系统就是其中的一项， 阿富汗战争期间， 声学定位技术被成功运用于狙击手定位和枪声检测领域， 取得了良好的效果， 被各国所重视. 目前的枪声定位系统五花八门， 在基阵的选择上有平面基阵、 正棱锥基阵和散布式分布的麦克风基阵， 这些基阵各有优势， 但也都有不可忽略的问题， 尤其是在对俯仰角、 方位角的估计上都存在一定的问题[1]， 主要由于目前的定位算法多是从智能地雷、 反直升机装备系统移植而来， 这些系统的俯仰角变化范围为0°～90°， 而枪声定位系统声源点的俯仰角变化一般在-45°～+45°之间， 在0°附近的应用尤为广泛， 文献[4，8]的研究均表明这些算法在俯仰角为0°附近的估算误差最大， 因此导致枪声系统的定位精度并不理想.

在对单基阵的研究中发现， 在影响因素相同的条件下， 对同一点进行检测， 实际误差值的正负与基阵的方向相关， 为改善俯仰角在0°附近的定向精度， 本文提出基于两个上下对称基阵的定位算法， 并对俯仰角测算进行了融合， 算法简单， 容易实现[2].

1声源点距离计算与仿真分析

图 1　麦克风基阵模型Fig.1　Microphone array model

1.1声源点距离估算

根据基阵麦克风的坐标关系可得方程组如式(1)所示[3]， 其中i取值为1～6

(1)

基于上述方程组， 对两个麦克风基阵分别处理， 与中心点的坐标表达式分别做差即可得两个关于x, y, z的三元一次方程组， 由于篇幅所限本文对方程组不再一一列出. 根据上下基阵所构成的两个方程组可分别求得x, y, z关于L的两套表达式， 两套表达式求得的x, y, z关于L的表达式分别对等即可得L关于声达距离差ri的3个表达式， 如式(2)所示：

1.2俯仰角、 方位角估算

图 2　上基阵定位模型Fig.2　The above array positioning model

以M1， M2， M3， M所组成的上基阵为例分析， 声源点俯仰角∠SOS′为θ1， 方位角∠S′OM1为α1， 如图 2 所示，M1,M2,M3共面， 分别做声源点S和中心麦克风M在该平面的投影S′和O， 若假设SO长度为L1， 根据坐标和角度关系， 利用余弦定理可将声源点到各麦克风的距离表达式记为式(3)所示形式[6].

(3)

将式(3)等式右侧的余弦展开后将后三项减去第一项， 左侧可写为(SMi-SM)(SMi+SM)， 当声源点距离远大于声达距离差时可写为2L1*ri， 可得关于θ1, α1的方程组如式(4)所示:

(4)

由式(4)即可求得俯仰角θ1的表达式为

(5)

同理， 对M4, M5, M6, M所组成的下基阵进行分析， 同样可以得到俯仰角θ2的表达式

(6)

俯仰角θ取两个基阵测量的均值， 即θ=(θ1+θ2)/2.

根据式(4)可将α表述为关于俯仰角θ和声达距离差ri的函数， 如式(7)所示:

(7)

方位角α取两个基阵测量的均值， 即α=(α1+α2)/2.

2声源点定位误差分析

本文对定位误差的分析仅考虑时延估计误差对定位精度的影响， 而对实际情况下基阵尺寸的测量误差、 电气设备数据采集与计算误差等不进行分析. 假设所有麦克风的时延估计标准偏差相等， 记为στ， 则声达时间差测量的标准偏差相等， 即σr1=σr2=σr3=σr4=σr5=σr6=σr， 且σr=C*στ.

2.1定距误差分析

式(2)中关于声源点距离L的表达式1, 2在后续的分析中误差大， 定距效果差， 在此不再进行分析， 仅对表达式(3)进行理论分析. 根据误差传播理论， 声源点距离估计的标准差可记为

(8)

根据俯仰角计算式(5)与式(6)， 反推可得

(9)

对式(2)中表达式③求偏导为

(10)

将L表达式以及公式(9)代入式(10)， 可得

(11)

将公式(11)代入式(8)， 可将测距误差表示为

(12)

根据测距误差表达式(12)知， 距离误差主要与基阵尺寸、 声源点距离、 俯仰角以及时延估计误差有关， 声源点距离越大， 误差越大， 适当的增大基阵尺寸能够有效地减小测距误差.

2.2俯仰角误差分析

根据俯仰角计算公式， 将俯仰角估计标准差记做σθ， 对θ的表达式求偏导

(13)

利用式(13)， 根据误差传播理论可将σθ记为

(14)

式(14)表明俯仰角误差主要与俯仰角本身、 基阵尺寸以及时延估计误差有关， 与方位角无关， 同时在俯仰角关系式(4)的推导过程中存在对声源点距离的近似计算， 因此在近距离条件下， 声源点距离对俯仰角误差也存在一定影响.

2.3方位角误差分析

将方位角估计标准差记为σα， 则其表达式可记为

(15)

分别对其表达式求偏导， 即

(16)

将式(17)和式(15)代入方位角估计标准差式(15)可得

(17)

根据俯仰角θ的取值范围为(-45°～45°)， 可将式(17)化简为

(18)

式(18)表明方位角误差主要与方位角、 俯仰角、 基阵尺寸和时延估计误差有关， 同时由于声源点距离对俯仰角的影响， 声源点距离在近距离条件下同样对方位角误差有一定影响.

3数据仿真

根据已有的研究表明[4,5]， 定位、 定向误差均与时延估计误差成正比， 与基阵臂长成反比， 本文不再进行赘述. 仿真中统一取基阵臂长d=0.25m， 时延估计误差Δτ=10μs， 基于实际应用场景将俯仰角的变化范围定为(-45°～45°).

图 3　声源点距离对距离误差影响Fig.3　Influence of sound source distance to the distance error

图 3 是关于式(2)中L的3个表达式进行的仿真， 俯仰角5°， 方位角45°. 曲线1为表达式(2a) 的仿真曲线， 曲线2为表达式(2a)的仿真曲线， 曲线3为表达式(2c)的仿真曲线. 由仿真曲线表明表达式(2a)和(2b)存在较大误差， 相比之下表达式(2c)误差较小， 相对误差在25%以内. 根据已知枪声定位系统的参数， 如美军Boomerang系统、 英军SWATS单兵系统、 中航三所的狙击手定位系统等， 距离相对误差的设计标准均为30%以内， 因此表达式(2c)能够被运用到实际探测中.

图 4 为俯仰角角度对距离估计误差的影响曲线， 方位角为45°， 从曲线弧度可以看出距离越大， 俯仰角对距离估计误差的影响越明显， 同时俯仰角为-10°～10°时对定距误差影响相对最小， 而该区域也是枪声定位系统应用最为频繁的区域.

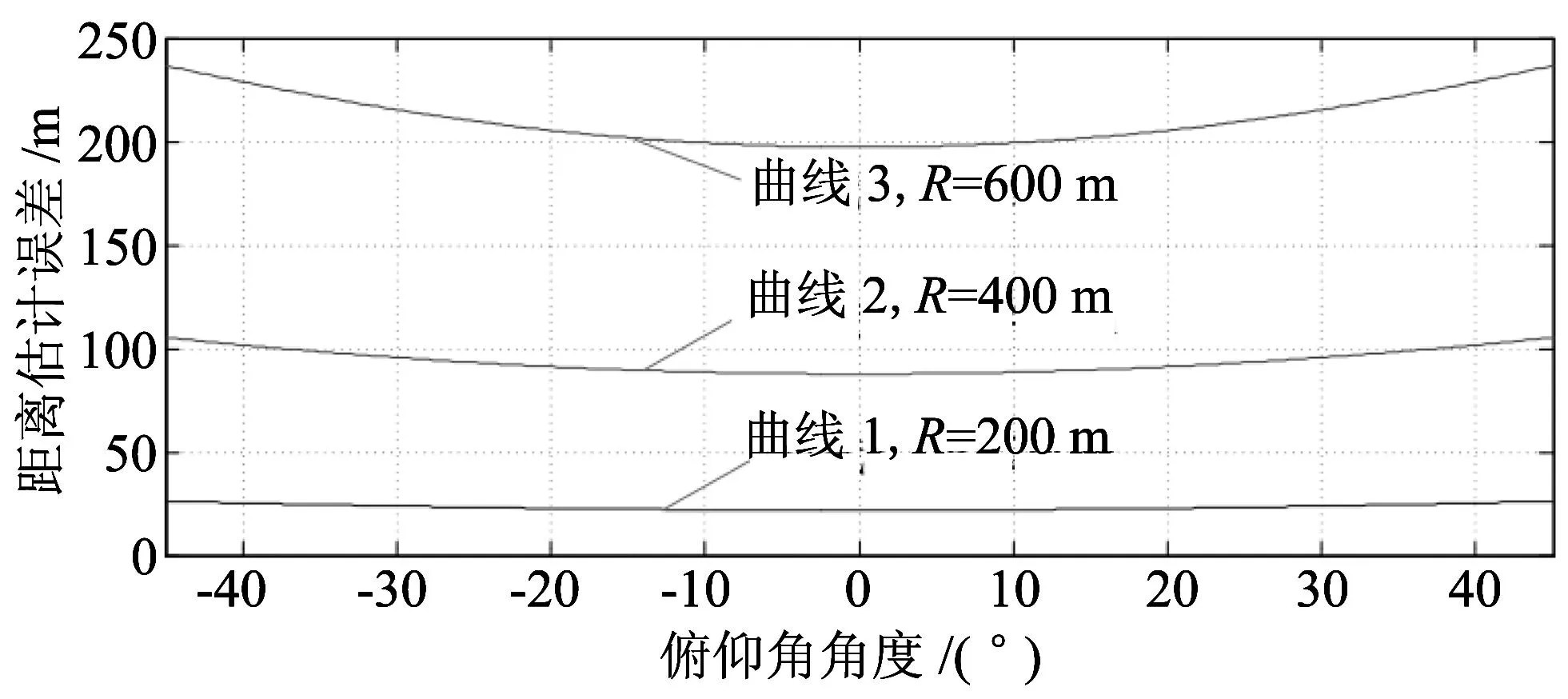
图 4　俯仰角角度对距离误差的影响Fig.4　Influence of pitch angle to the distance error

图 5　声源点距离对俯仰角误差影响Fig.5　Influence of sound source distance to the pitch angle error

如图 5 所示， 曲线1为上基阵仿真曲线， 曲线2为下基阵仿真曲线， 可见在近距离情况下俯仰角误差较大， 这是由于在对公式(4)的推导近似时近距离条件下Li与声达距离差ri相差数量级达不到近似要求， 因而导致的误差较大. 融合后误差与距离关系如曲线3所示， 俯仰角估计精度明显提高， 尤其是在150m以内的近距离范围有明显改善， 图 6 为俯仰角自身对定向估计的影响， 图中截去的两个峰值点均为-2.63°， 仿真表明俯仰角变化对俯仰角估计的影响不大， 系统的俯仰角误差整体控制在±3°以内.

图 7 为声源点距离对方位角误差的影响曲线， 曲线1为上基阵误差， 曲线2为下基阵误差， 曲线3为融合后误差. 受俯仰角的影响， 在近距离条件下声源点距离对方位角误差影响也比较大， 取均值后有明显改善. 俯仰角对方位角误差的影响如图 8 所示， 在±30°左右会有明显的峰值点， 在常用范围内影响较小. 方位角自身对其估计误差的影响如图 9 所示， 俯仰角为图 8 中的峰值点即30°， 仿真曲线显示在俯仰角影响最为显著的时候方位角对其自身估计误差的影响也比较小， 除去160°的峰值点为6.7°， 整体误差水平能够控制在±5°， 定位精度整体较高.

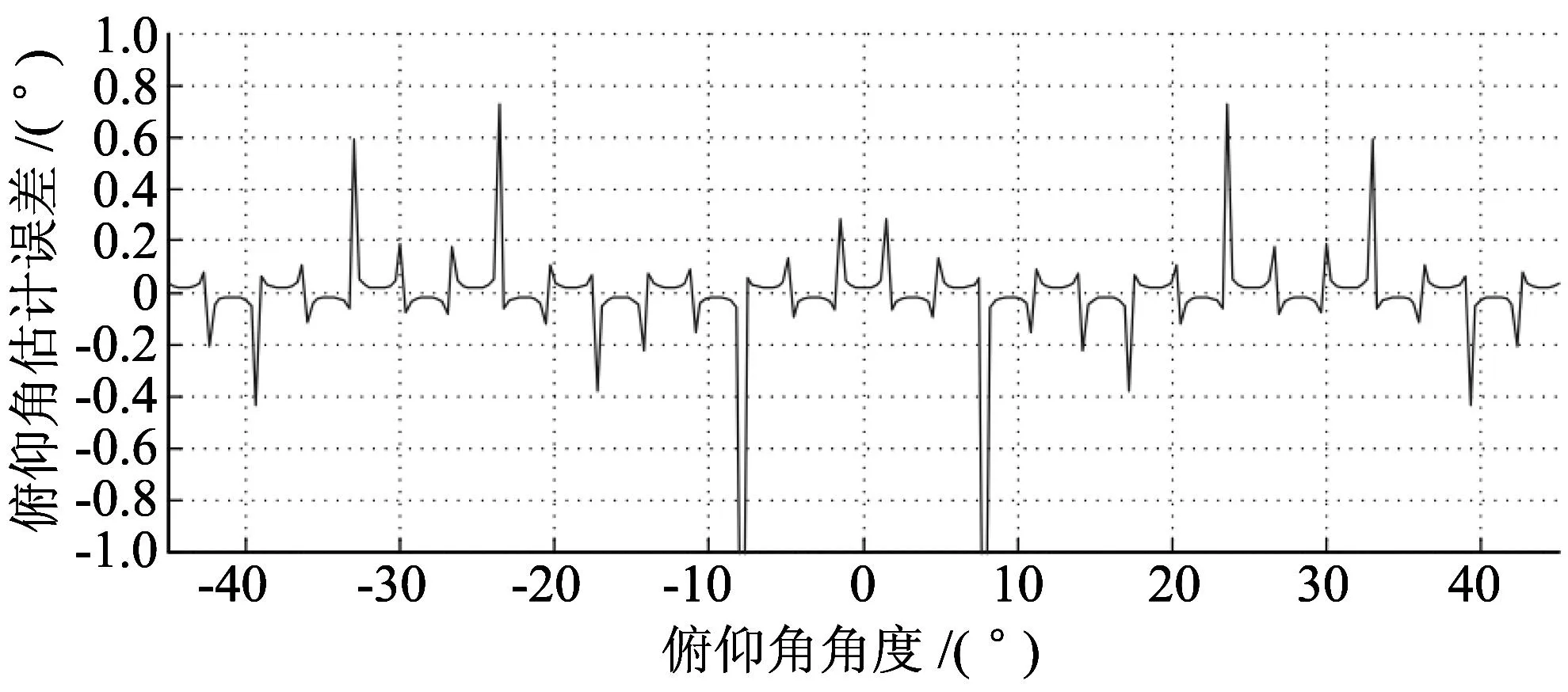
图 6　俯仰角角度对俯仰角误差的影响Fig.6　Influence of pitch angle to the pitch angle error

图 7　声源点距离对方位角误差的影响Fig.7　 Influence of sound source distance to the azimuth error

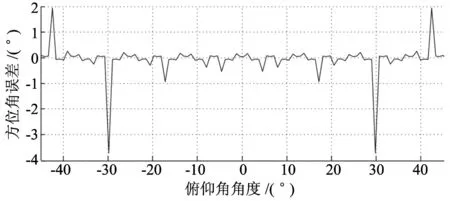
图 8　俯仰角角度对方位角误差的影响Fig.8　Influence of pitch angle to the azimuth error

图 9　方位角角度对方位角误差的影响Fig.9　 Influence of azimuth to the azimuth error

4结论

文章基于枪声定位系统的特点提出了对称基阵分析定位的方法， 通过仿真分析可知， 提出的算法使得对声源点俯仰角和方位角的估算误差得到明显改善， 提高了定向的精度. 在爆轰波传播的有效距离内， 文章提出的基阵和算法在近距离条件下能够实现定向、 定位， 在较远距离条件下能够实现较为精准的定向， 系统能够被运用到固定监测点和低速车载系统中， 具有实用价值.

参考文献：

[1]AguilarJR.Gunshotlocationsystems-thetransferofthesniperdetectiontechnologyfrommilitarytocivilianapplications[C].ICCST,Carnahan, 2013: 1-6.

[2]ParedesDM,ApolinárioJrJA.ShooterlocalizationbasedonDOAestimationofgunshotsignalsanddigitalmapinformation[J].IEEELat.Am.Trans., 2015, 13(2): 441-447.

[3]吕玉涛, 安亚亮, 衣锦辉. 狙击手声被动定位模型仿真分析[J]. 系统仿真技术, 2012, 8(2): 138-143.

LvYutao,AnYaliang,YiJinhui.Simulationofsniperlocalizationbyacoustictechnical[J].SystemSimulationTechnology, 2012, 8(2): 138-143. (inChinese)

[4]孙书学, 顾晓辉, 孙晓霞. 用正四棱锥形阵对声目标定位研究[J]. 应用声学, 2006, 25(2): 102-108.

SunShuxue,GuXiaohui,SunXiaoxia.Studyonlocalizationofacoustictargetwitharectangularpyramidarray[J].J.Appl.Acoust., 2006, 25(2): 102-108. (inChinese)

[5]陈华伟, 赵俊渭, 郭业才. 五元十字阵被动声定位算法及其性能研究[J]. 控制与探测学报, 2003, 25(4): 11-16.

ChenHuawei,ZhaoJunwei,GuoYecai.Acousticpassivelocalizationalgorithmbasedonaplanarfive-elementarrayanditsperformanceanalysis[J].JournalofDetection&Control, 2003, 25(4): 11-16. (inChinese)

[6]祝石龙, 庄志洪, 张清泰. 利用圆阵实现声目标的全空域被动位[J]. 声学学报, 1999, 24(2): 204-209.

ZhuShilong,ZhuangZhihong,ZhangQingtai.Anomni-directionalpassivelocalizationtechnologyofacoustictargetwithplancirclearray[J].Acta.Acoust., 1999, 24(2): 204-209. (inChinese)

[7]李京华, 施坤林, 揭涛, 等. 空气中被动声测向系统的误差分析[J]. 控制与探测学报, 1999, 21(1): 29-34.

LiJinghua,ShiKunlin,JieTao,etal.Erroranalysisofapassiveacousticdetectingdirectionsysteminair[J].JournalofDetection&Control, 1999, 21(1): 29-34. (inChinese)

[8]林晓东, 吴松林, 张川. 六元探测基阵被动声定位算法及其性能研究[J]. 声学技术, 2008, 27(2): 192-196.

LinXiaodong,WuSonglin,ZhangChuan.Passiveacousticlocationalgorithmbasedonasix-elementdetectionarrayanditsperformanceanalysis[J].TechnicalAcoustics, 2008, 27(2): 192-196. (inChinese)

Research on Gunshot Location Algorithm Based on Symmetric Microphone Array

DANG Cunlu1,2, YU Guangzu1,2, GUO Yongji1,2

(1. College of Electrical and Information Engineering, Lanzhou University of Technology, Lanzhou 730050, China;2. Key Laboratory of Gansu Advanced Control for Industrial Processes, Lanzhou 730050, China)

Abstract:In order to improve the performance of the gunshot location system, this paper puts forward the method of dual microphone array symmetrical layout. Seven microphones is used to constitute the symmetry of two rectangular pyramid array, and formula is derived respectively to the distance,the pitch angle and the azimuth angle.Physical model is built to simulate and analyze fixed distance and orientation errors, and analyze the double-base array pitch error and data fusion. Research shows that this array model performance of direction is improved obviously, which can be applied to the fixed or low speed vehicle monitoring system.It can realize probe the gunshot location in short distance and the gunshot direction in long distance.

Key words:gunshot location; symmetric array; error analysis; direction; distance

中图分类号:TN912

文献标识码:A

doi:10.3969/j.issn.1671-7449.2016.01.014

作者简介：党存禄(1964-), 男， 教授， 博士， 主要从事电力电子与电力传动的研究.

收稿日期:2015-08-30

文章编号:1671-7449(2016)01-0074-06