一种新型小型化交叉耦合带通滤波器的设计

马润波， 闫建国， 陈新伟， 闫丽云， 韩丽萍

(山西大学 物理电子工程学院, 山西太原 030006)



一种新型小型化交叉耦合带通滤波器的设计

马润波， 闫建国， 陈新伟， 闫丽云， 韩丽萍

(山西大学 物理电子工程学院, 山西太原 030006)

摘要:本文设计了一种基于阶跃阻抗谐振器的新型嵌入式交叉耦合带通滤波器. 为使滤波器小型化， 设计了两种紧凑型阶跃阻抗谐振器结构. 通过研究和改善谐振器间的耦合机制， 可使两种谐振器不仅形成嵌入式结构， 而且缩减了馈线占据的面积， 进一步减小了含馈线在内整个带通滤波器的尺寸. 为验证此方法的可行性， 利用滤波器综合法设计了一个中心频率为2.4 GHz， 相对带宽FBW为15%的4阶交叉耦合带通滤波器， 其最终设计尺寸为28 mm×20 mm(0.37λspan×0.26λspan，λspan为中心频率所对应的导波波长). 对该滤波器进行了仿真、 加工和测试， 结果表明该滤波器具有所需的广义切比雪夫特性， 且互相吻合得很好.

关键词:阶跃阻抗谐振器； 交叉耦合； 带通滤波器； 传输零点； 小型化

针对微波通信系统中小型化和高性能滤波器的设计， 众多研究者提出了各种有效的方法和结构， 其中平面结构滤波器由于具有结构紧凑、 易于加工的特点而被广泛应用. 谐振器作为滤波器中的基本单元， 对滤波器的尺寸和性能有直接影响. 例如， 采用开路半波长平行耦合线作为谐振器是常见的滤波器设计方法， 为克服其尺寸过大的缺陷[1]， 经常将平行耦合线弯折， 形成发夹型谐振器以减小尺寸是许多设计采用的方法[2]. 此外， Makimoto等学者提出了阶跃阻抗谐振器(SIR)， 可以明显减小谐振器尺寸， 同时还能够灵活控制第一杂散频率[3]. 文献[4]采用了改进的发夹型SIR， 而且谐振器末端的耦合线部分相当于加载了一个电容， 实现了进一步减小谐振器尺寸的目的.

除谐振器外， 滤波器的拓扑结构是影响其尺寸和性能的重要因素. 与传统的巴特沃兹和切比雪夫响应型滤波器相比， 广义切比雪夫响应滤波器通过在边带和阻带内引入传输零点的方法来提高滤波器的选择性和带外抑制特性， 由Cameron等学者逐渐完善了对应的广义耦合矩阵综合方法[5]， 并出现了众多的交叉耦合滤波器设计方法[6-8]. 结合谐振器结构和交叉耦合设计方法， 文献[9]设计了一种嵌入式的交叉耦合拓扑结构， 在较大程度上减小了滤波器的尺寸.

为充分满足现代通信系统对微波器件小型化越来越高的需求， 本文基于发夹型阶跃阻抗谐振器和一种新颖的弯折小型化阶跃阻抗谐振器， 采用嵌入式的交叉耦合拓扑结构， 设计了一个中心频率为2.4 GHz， 相对带宽为15%的小型化四阶交叉耦合带通滤波器， 并经仿真、 加工和测试验证了其性能.

1滤波器结构及其小型化谐振器

本文设计的带通滤波器采用了Rogers RO 4350介质基板， 其相对介电常数εr=3.48， 基板厚度h=0.762 mm， 包含上下两层金属， 下层金属为地层， 上层金属为谐振器层. 图 1 给出了谐振器层所包含的4个谐振器及馈线结构.

图 1　滤波器结构图Fig.1　The structure of the proposed filter

由于谐振器大小决定着滤波器的整体尺寸， 本文设计了两种基于半波长SIR的小型化结构， 分别对应图1中类似发夹型的谐振器1与4以及充分弯折的谐振器2和3. 在结构的具体设计中， 首先考虑了以下几种方法来减小谐振器尺寸：

1) 两种谐振器都采用了阶跃阻抗结构， 可以减小谐振器的电长度. 考虑到后面设计的滤波器实际工作于2.4 GHz， 并设定两种半波长SIR的阻抗比分别为0.81和0.88， 则根据文献[10]提到的SIR特性， 可得两种谐振器的物理长度均大约为31 mm；

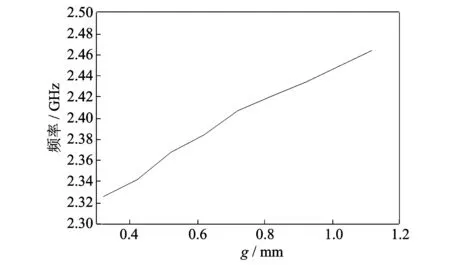
图 2　谐振频率f随缝隙宽度g的变化曲线Fig.2　The relationship between f and g

2) 对SIR谐振器进行结构弯折可以充分利用有效面积. 在谐振器总长度不变的情况下， 结合CST三维电磁仿真软件， 经优化和微调最终确定图1中各谐振器及50 Ω馈线的结构参数分别为：h1=10.6 mm，h2=12.72 mm，h3=1.4 mm，h4=1 mm，h5=1 mm，h6=1.4 mm，w1=0.9 mm，w2=1.14 mm，w3=0.5 mm，w4=0.8 mm，w5=1.73 mm，w6=0.4 mm，l1=4.5 mm，l2=1.5 mm，l3=9.5 mm，l4=1.5 mm，l5=5.5 mm，l6=0.3 mm，l7=0.6 mm，l8=3.45 mm；

3) 谐振器2和3中间的平行耦合线间距为g， 且靠近谐振器开路端具有明显的电容效应， 等效为在谐振器开路端加载电容[4]， 相当于增加了谐振器有效电长度， 减小了物理尺寸. 在保持谐振器2和3金属总长度不变的情况下， 图 2 给出了其谐振频率f随间距g的变化曲线. 可以看出，f随g的减小逐渐减小， 这有利于谐振器2和3的小型化. 此处选择g=0.72 mm以实现2.4 GHz谐振.

此外， 在图 1 所示滤波器结构中的谐振器1与4的开路端具有较强的电场分布， 它们相互之间经缝隙s14可以实现电耦合； 而谐振器2和3的相邻部分具有强电流分布特点， 经其间缝隙s23可实现磁耦合. 一般来讲， 在利用综合法设计滤波器的过程中， 电耦合系数要远小于磁耦合系数和混合耦合系数. 为了得到较小的耦合系数， 就需要加大电容耦合两谐振器间的距离， 从而增大滤波器的尺寸， 不利于小型化. 而本文设计的谐振器1和4之间的耦合面积较小， 所以很小的缝隙s14即可满足较小电耦合系数的要求.

通过上述方法， 谐振器2与3具有很小的尺寸， 可以分别被嵌入到谐振器1和4内部. 这不仅能够充分减小整个滤波器的尺寸， 而且便于实现各谐振器间的耦合. 此处谐振器1与2之间、 3与4之间则通过缝隙s12实现混合电磁耦合. 与传统交叉耦合拓扑结构相比， 嵌入式结构的尺寸减小约50%.

更进一步， 得益于尺寸非常小的谐振器2、 3， 发夹型谐振器1、 4即使在分别嵌入它们之后， 内部仍然具有很大空隙(如图1虚线所示). 因此， 可以将谐振器1、 4的中部宽度为w3的传输线向内弯折， 一方面实现了空间的充分利用， 另一方面可以将馈线向结构内侧牵引， 这实现了对含馈线在内整个带通滤波器的充分小型化. 值得一提的是， 虽然此时谐振器1的宽度为w3的传输线， 与谐振器2的开路端的间距变得较近， 但由于它们附近分别呈现出强磁场和强电场的特性， 相互之间的耦合很小， 因此谐振器1与2之间主要还是通过缝隙s12实现混合电磁耦合， 谐振器3与4之间也一样. 由此可见， 各谐振器间的耦合可以通过不同的缝隙独立调节， 这能够减少设计的复杂性. 此外， 由于谐振器1、 4向内弯折， 馈电点的位置可以在不改变电路尺寸的情况下进行大范围灵活调节， 这使得外品质因数Qe具有较大的可调范围， 能够满足不同带宽滤波器的设计需求.

2滤波器综合设计

本文预设交叉耦合带通滤波器的中心频率为2.4 GHz， 相对带宽为15%， 以此为指标按图 3 所示拓扑结构设计4阶广义切比雪夫响应滤波器， 并具体由图 1 所示滤波器结构来实现. 由文献[11]可得对应的低通原型中各元件值：g1=0.959 7，g2=1.421 9，J1=-0.210 8，J2=1.117 7. 由此计算出满足该指标滤波器所需的耦合系数及外品质因数分别为

(1)

(2)

(3)

(4)

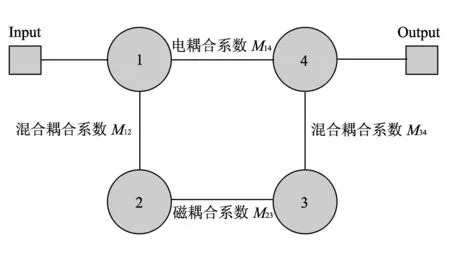
图 3　带通滤波器的拓扑结构Fig.3　The topological structure of the BPF

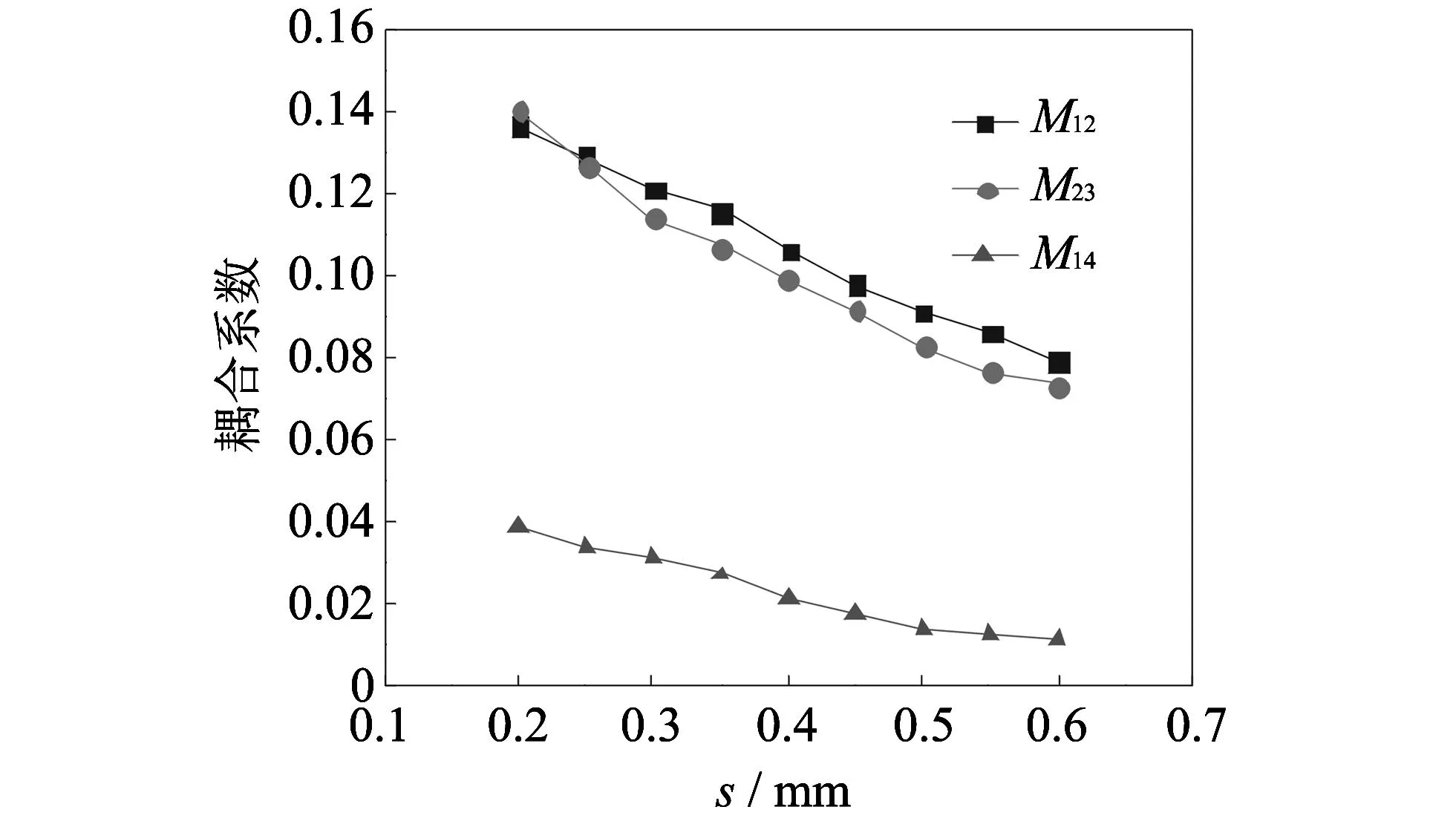
图 4　耦合系数Mij的绝对值随谐振器间距离sij变化曲线Fig.4　The relationship between the absolute value of Mijand sij

耦合系数是直接影响滤波器指标及性能的重要参数. 在交叉耦合带通滤波器的设计中， 为了实现传输零点， 需同时满足3种类型的耦合， 即电耦合、 磁耦合及混合耦合. 根据文献[11]， 利用弱耦合法提取谐振器间的耦合系数， 若得到的特征频率分别为fa和fb， 则可由此计算出

(5)

图 4 是耦合系数Mij的绝对值(i,j分别代表谐振器编号， 其中电耦合系数M14为负值)随对应两谐振器间距离sij的变化曲线. 可以看出， 随着谐振器间的距离变大， 耦合系数的绝对值逐渐减小.

除耦合系数外， 滤波器设计过程中另一个关键参数为外品质因数. 外品质因数的提取可利用图 5 所示拓扑结构完成， 从而确定抽头的位置t. 由文献[11]可知

(6)

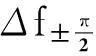
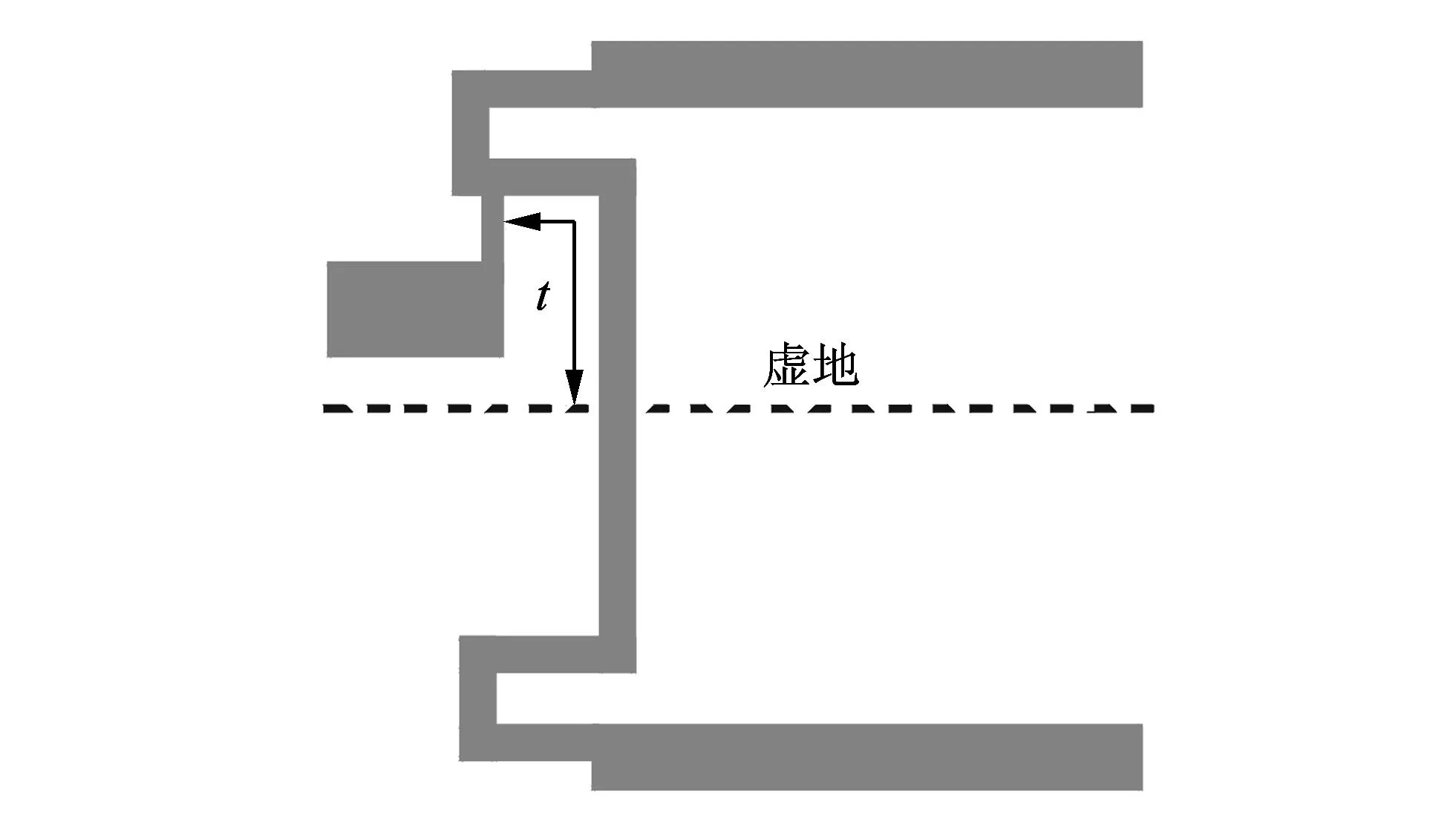
图 5　抽头线耦合结构图Fig.5　The tapped line coupling structure

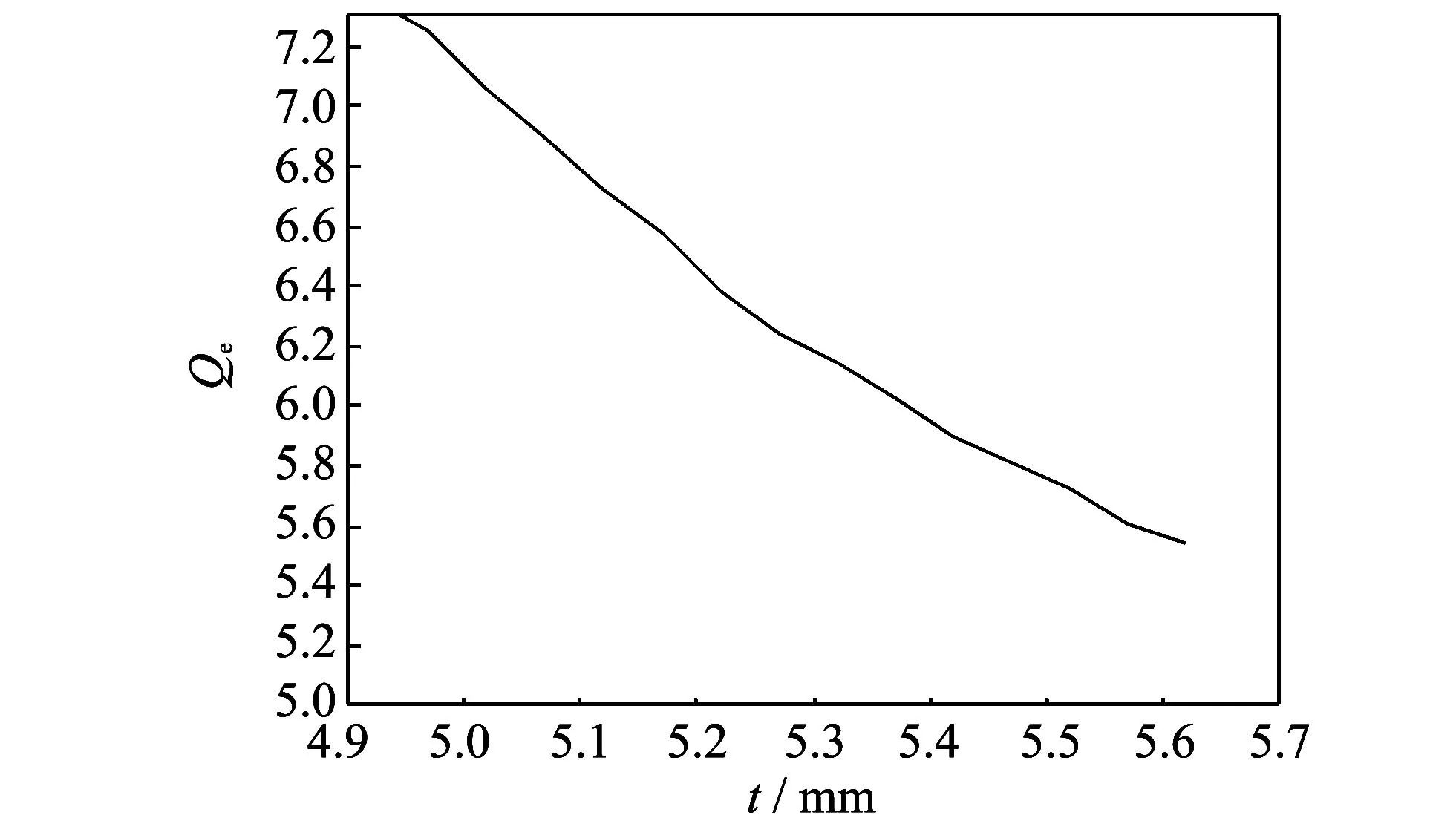
图 6　外品质因数Qe随t的变化曲线Fig.6　The relationship between Qeand t

根据图 4 和图 6 中的曲线， 可最终确定谐振器间的间距分别为s12=0.27 mm，s23=0.327 mm，s14=0.28 mm； 抽头的位置t=5.22 mm.

3仿真及测试结果

为了检验本文设计交叉耦合带通滤波器的性能， 我们对综合设计出的滤波器进行了仿真、 加工和测试. 图 7 为所加工的滤波器实物图， 其尺寸为28 mm × 20 mm (0.37λg×0.26λg).

图 7　滤波器实物图Fig.7　The photograph of the filter

图 8　滤波器的仿真及测试S参数曲线Fig.8　The simulated and measured S-parameter results

使用矢量网络分析仪Agilent N5230A对加工滤波器的S参数进行了测量. 图 8 给出了该滤波器的仿真与测试结果的S参数曲线. 从图中可以看出仿真中心频率位于2.4 GHz处， -3 dB的通频带范围为： 2 207 MHz～2 576 MHz， 相对带宽约为15.4%. 通带内的反射系数小于-14 dB， 插入损耗为 0.8 dB. 测试的中心频率位于2.37 GHz处， -3 dB通频带范围为： 2 205 MHz～2 545 MHz， 相对带宽约为14.5%. 通带内的反射系数小于-10 dB， 插入损耗约为1.5 dB. 通带较为平坦， 在2.09 GHz和 2.71 GHz 处分别有一个传输零点， 从而使边缘变得更加陡峭， 提高了滤波器的边缘选择特性， 而带外抑制优于25 dB， 这表明该滤波器具有良好的通带和阻带特性.

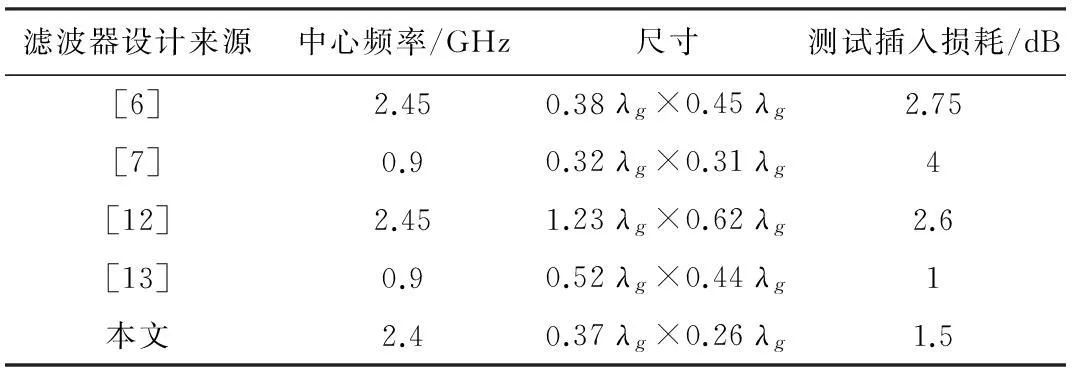
表 1　参考文献滤波器及本文设计滤波器对照表

表 1 为本文设计的滤波器与文献中设计的滤波器在尺寸及性能方面的对比， 其中λg为各滤波器中心频率对应的导波波长. 可见， 本文所设计滤波器在具有较小尺寸的条件下， 仍然保持了较低的插入损耗， 这反映了该滤波器能够满足小型化和高性能的要求， 本文提出的滤波器结构具有较小的尺寸和较低的插入损耗.

4结论

本文利用滤波器综合法设计了一个中心频率为2.4 GHz， 相对带宽FBW为15%的小型化4阶平面交叉耦合带通滤波器. 为使滤波器小型化， 设计了两种紧凑型阶跃阻抗谐振器结构. 通过研究和改善谐振器间的耦合机制， 两种谐振器不仅可实现嵌入式结构， 而且能把馈线向结构内侧牵引， 进一步实现了含馈线在内整个带通滤波器的小型化. 滤波器最终尺寸为28 mm×20 mm(0.37λg× 0.26λg)， 且具有结构简单， 易于加工的特点. 对该滤波器进行加工测试， 实测结果和仿真结果基本吻合， 结果表明该设计具有较低插入损耗及良好的边缘选择性和带外抑制特性， 能够满足现代通信系统对小型化高性能滤波器的要求.

参考文献：

[1]Cohn S B. Parallel-coupled transmission-line-resonator filters[J]. IRE Trans. Microwave Theory Tech., 1958, 6(2): 223-231.

[2]Cristal E G, Frankel S. Hairpin-line and hybrid hairpinline/half-wave parallel-coupled-line filters[J]. IEEE Trans. Microwave Theory Tech., 1972, 20(11): 719-728.

[3]Makimoto M, Yamashita S. Bandpass filters using parallel coupled strip-line stepped impedance resonators[C]. Microwave symposium Digest, 1980 IEEE MTT-S International, Washington: IEEE, 1980: 141-143.

[4]Sagawa M, Takahashi K, Makimoto M. Miniaturized hairpin resonator filters and their application to receiver front-end MIC’s[J]. IEEE Trans. Microwave Theory Tech., 1989, 37(12): 1991-1997.

[5]Cameron R. General coupling matrix synthesis methods for chebyshev filtering functions[J]. IEEE Trans. Microwave Theory Tech., 1999, 47(4): 433-442.

[6]Tsai L C. Design of bandpass filters using miniaturized stepped-impedance resonators[C]. Wireless Communications, Networking and Mobile Computing (WiCOM), 2011 7th International Conference, Harbin :IEEE, 2011: 1-4.

[7]Nedelchev M. Design of microstrip meander-folded hairpin resonator filters[C]. Microwave Techniques (COMITE), Pardubice: IEEE, 2013: 69-72.

[8]Deng Pu Hua, Tsai J T. Design of microstrip cross-coupled bandpass filter with multiple independent designable transmission zeros using branch-line resonators[J]. Microwave and Wireless Components Letters, IEEE, 2013, 23(5): 249-251.

[9]Chaimool S, Akkaraekthalinl P. Resonator-embedded four-pole cross-coupled dual-band microstrip bandpass filters[C]. Communications and Information Technologies, 2006. ISCIT '06. International Symposium, Bangkok: IEEE, 2006: 1076-1079.

[10]Sagawa M, Makimoto M, Yamashita S. Geometrical structures and fundamental characteristics of microwave stepped-impedance resonators[J]. IEEE Trans. Microw. Theory Tech., 1997, 45(7): 1078-1085.

[11]Hong Jia Sheng, Lancaster M J. Microstrip filters for RF/microwave applications[M]. 1st, New York: Wiley, 2001: 235-319.

[12]Li Jiankang, Chen Chunhong, Wu Wen. Design of dual-passband cross-coupled filter using stub-loaded open-loop resonators[C]. Microwave Conference, 2009. APMC 2009. Asia Pacific, Singapore: IEEE, 2009: 929-932.

[13]Chang K F, Tam K W. Miniaturized cross-coupled filter with second and third spurious responses suppression[J]. Microwave and Wireless Components Letters, IEEE, 2005, 15(2): 122-124.

Design of the Novel Miniaturized Cross-Coupled Band-Pass Filter

MA Runbo, YAN Jianguo, CHEN Xinwei, YAN Liyun, HAN Liping

(College of Physics and Electronic Engineering, Shanxi University, Taiyuan 030006, China)

Abstract:A novel embedded cross-coupled filter based on stepped impedance resonators is proposed in this paper. Two kinds of compact stepped impedance resonator structures are designed to realize the miniaturization of the filter. By studying and improving the coupling mechanism, the two resonators can not only form the embedded structure, but also reduce the area occupied by the feed line, which further reduce the size of the whole band-pass filter including the feed structure. In order to verify the feasibility of this approach, fourth-order cross-coupled band-pass filter with center frequency of 2.4 GHz and relative bandwidth of 15% was designed by using filter synthesis method.. The filter occupies a very small size of 28 mm×20 mm(0.37λspan× 0.26λspan，whereλspanis the guided wavelength corresponding with the center frequency). Finally it is fabricated and measured. The measured and simulated results show that the filter has the generalized Chebyshev characteristics，and they match each other very well.

Key words:stepped impedance resonator; cross-coupled; band-pass filter； transmission zeros; miniaturization

中图分类号:TN713+.5

文献标识码:A

doi:10.3969/j.issn.1671-7449.2016.01.013

作者简介：马润波(1974-)， 男， 副教授， 博士，主要从事平面天线、 微波器件和电路的研究.

基金项目：山西省自然科学基金资助项目(2012011013-3)； 山西省青年科学基金资助项目(2010021015-1， 2014021021-1)

收稿日期:2015-11-01

文章编号:1671-7449(2016)01-0069-05