可变荷载对结构模态分析评定影响的讨论

高洪健， 刘　坤， 郭　娇

(1. 河北工业大学 土木工程学院， 天津 300401； 2. 河北工业大学 校园规划处， 天津 300401)



可变荷载对结构模态分析评定影响的讨论

高洪健1， 刘坤2， 郭娇1

(1. 河北工业大学 土木工程学院， 天津 300401； 2. 河北工业大学 校园规划处， 天津 300401)

摘要:通过试验方法获得结构的动力特性， 以进一步对结构的分析模型做出评定. 为了评估建筑结构中可变荷载计入体系质量矩阵后对结构自振频率的影响， 本文经理论分析以及应用结构分析软件进行建模分析两种方法， 分析了建筑结构体系中折算活荷载计入体系质量矩阵前后结构较低阶固有频率的变化， 认为对于设计时可变荷载较大的高层及超高层建筑主体， 在完工初期进行结构的动力特性测试时若先考虑可变荷载对其自振频率的影响， 再对结构进行整体评价， 得出的结果将更加理想.

关键词:可变荷载； 结构模态分析； 动力特性测试

0引言

建筑结构的固有频率是损伤识别和动力特性测试中的重要参数， 其测试和分析一直被工程界所重视， 当前的许多研究都集中在模态参数识别的优化等方面. 然而， 多数测试结果都是与理论计算所得结构的自振周期或自振频率进行比较[1]， 进而评定结构的分析模型或者整体刚度. 对于结构主体刚刚完工且人员及机械设备没有进场的建筑结构来说， 理论计算的结构质量矩阵中往往计入了折算后的可变荷载. 这一状况会造成理论计算所得体系的固有频率偏小， 进而对上述结构的整体评定产生不利影响.

为了研究建筑结构的质量矩阵中计入折算以后可变荷载的影响， 以便更加准确地利用实验与理论计算所得结构的固有频率数据对建筑结构进行评定， 在进行理论分析的同时， 分别针对属于超限高层的河北工业大学图书馆结构及不同层数的普通框架结构进行计算， 望对今后建筑结构的动力特性测试及分析工作有一定的帮助.

1体系固有频率的求解

1.1结构分析模型

建立结构分析模型的方法有很多. 若应用集中质量法[2,3]， 可将结构体系离散成有限多自由度系统， 其分析模型即层间模型； 若将梁、 柱等主要构件视为杆件[4]， 并将质量集中于各个梁柱节点上， 得到的分析模型即杆系模型. 两种模型如图 1， 图 2 所示.

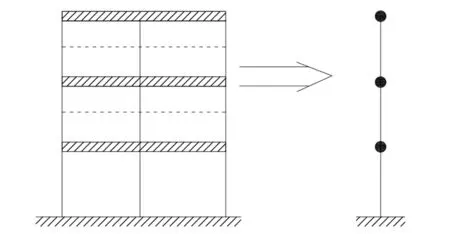
图 1　层间分析模型Fig.1　Analysismodel of story

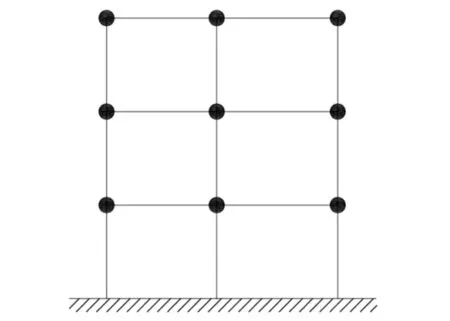
图 2　杆系模型Fig.2　Member system model

除此之外， 还有层间—杆系组合模型以及能够更好解决含有多塔结构、 弹性楼板等复杂工程问题的有限元模型. 无论采用何种计算模型， 归根结底是将质量连续分布的结构整体离散为自由度数目大大减小的多自由度体系， 进而简化计算的复杂性， 提高工程效率.

1.2求解系统固有频率数值的方法

工程中阻尼比的存在对于结构自振周期的影响很小[5]， 所以实际常采用无阻尼系统自由振动微分方程求解得到的各阶频率来表征建筑结构的动力特性. 借助计算机， 可以更加高效地求解经离散后多自由度体系的固有频率及振型.

简谐振动中， 离散后多自由度体系的最大动能及势能可分别表示为

(1)

(2)

根据能量守恒定律， 可得

(3)

进而推导出

(4)

式中：K,M分别为体系的刚度和质量矩阵；ψ,ψT分别为系统的振型矩阵及其转置矩阵. 若将系统的主振型近似假设为

(5)

式中：φ1,φ2,…,φm为假设的m个振型. 若另n×m阶矩阵φ及m维列矢量a分别为

(6)

则式(5)可表示为

(7)

把式(7)代入式(4)可得到

(8)

通过式(8)可以看出， R(ψ)在体系真实主振型处存在驻值， 且各驻值点对应的即为各阶固有频点pi. 为确定a中各元素值， 对式(8)求偏导数可得

(9)

式中： S(a)=aTφTMφa, Q(a)=aTφTKφa， 代入并化简后可得到

(10)

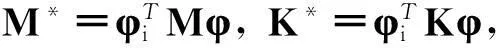
(11)

式中：K*,M*即为缩减为m个自由度后新体系的刚度及质量矩阵. 通过求解式(11)的特征方程， 即可求得多自由系统的前m阶固有频率及其振型. 应用上述方法估算结构体系的自振频率及振型称为Ritz法. 此外， 矩阵位移法及由Ritz法衍生出来的子空间迭代方法都常被应用于计算机系统， 并且能够得到结构体系自振频率及振型的较好估算[6]. 对于应用有限元技术的复杂工程， 其结果的精确程度取决于单元体的划分. 值得注意的是， 其迭代结果总是精确地接近体系固有频率的上限.

2固有频率的影响因素

2.1主质量矩阵

由式(11)可以进一步求得多自由度体系的第i阶固有(圆)频率， 可表示为

(12)

通过式(12)可知， 结构刚度和质量的变化会改变结构的固有频率. 文献[7]证明当质量的变化率为正时， 固有频率的变化率为负， 其表示式为

(13)

(14)

分析可知， 频率随质量的相对变化率受各阶频率值及振型的影响， 也受结构高度的影响.

2.2建筑结构的质量

结构设计时， 建筑物的重量由重力荷载代表值即永久荷载及可变荷载两部分组成. 永久荷载由体系中梁、 柱、 支撑等主要构件的自重组成， 可变荷载是由各层的人、 设备等活荷载以及风荷载和雪荷载等构成的. 根据我国规范规定[3,8]， 建筑的重力荷载代表值应取结构和构件自重标准值及可变荷载组合值之和. 可见， 适当增大结构的中可变荷载能够使结构在进行承载能力设计和抗震设计时有更高的安全储备.

对于结构的质量， 由于折算后可变荷载的计入， 势必会对结构的各阶振型产生一定的影响， 进而使分析结果偏离真实结果. 由式(12)可知， 如果在计算结构的质量矩阵时采用考虑组合值系数的方法计入可变荷载， 将使建筑结构的自振频率变小， 而这一误差使测试人员主观判定结构的整体刚度偏小. 对于同一栋建筑， 主体完工到进入正常使用期间， 质量对其固有频率的影响比刚度更加重要[9].

以上分析可知， 当通过测试方法得出结构的各阶模态参数时， 不能盲目的与设计资料进行对比， 进而对结构分析建模或结构整体刚度进行评估. 要针对结构当前的使用状况对设计资料进行有依据的修改， 以得出正确的分析结果.

3计算实例

为研究可变荷载对复杂结构体系固有频率影响的大小， 应用ETABS对河北工业大学图书馆进行建模分析， 其分析模型如图 3 所示.

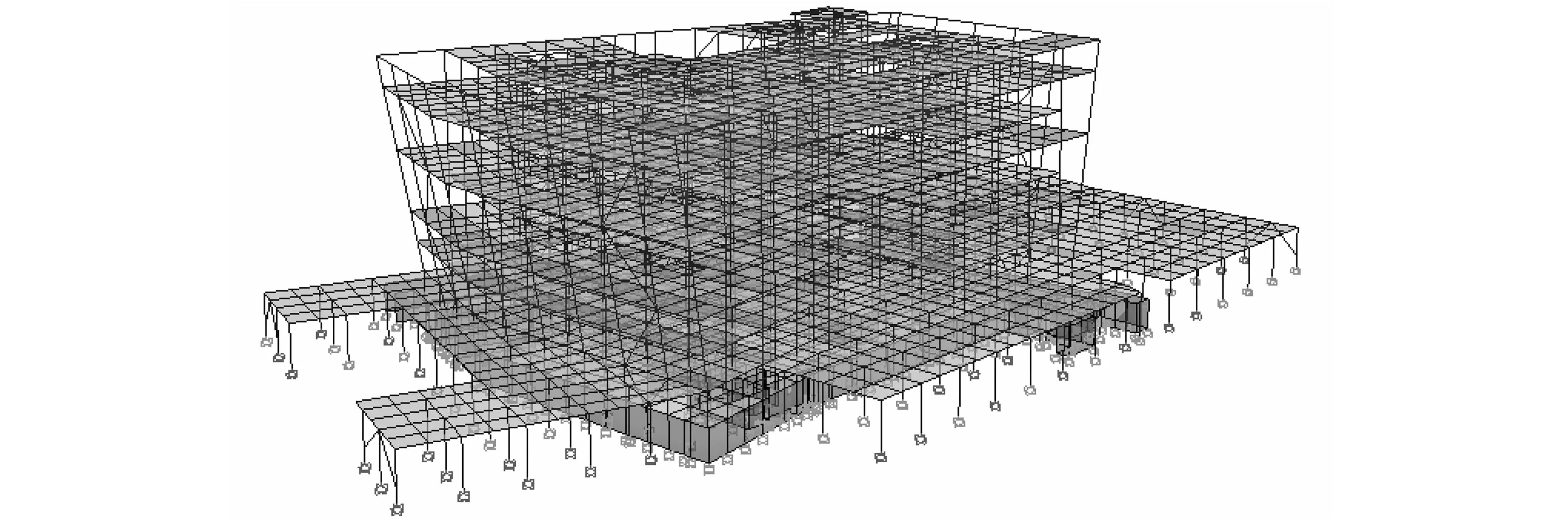
图 3　河北工业大学图书馆结构分析模型Fig.3　Structural analysis model of library of hebei university of technology

图 4　普通框架模型Fig.4　Ordinary frame model

分别计算该钢筋混凝土框架结构体系在计入及不计入可变荷载情况下前3阶的固有频率， 其数值及差值率见表 1.

对于普通的钢筋混凝土框架结构， 应用ETABS对一栋4榀 3跨的12层房屋进行结构分析. 其中按照规范要求定义楼面活荷载为2kN/m2， 考虑到进行动力特性房屋的重要性， 定义屋面活荷为3kN/m2， 并取可变荷载组合值系数为0.5[3,10]. 其分析模型如图 4 所示.

在保持各层构件不变的情况下， 削减楼层数目， 分析计入可变荷载前后的4层、 8层结构体系中前3阶的固有频率及差值率， 结果列于表 2 中.

由表 1， 表 2 可以看出， 随着框架结构层数的增多， 可变荷载对结构体系自振频率的影响呈增大趋势， 对于中高层结构的影响在5%左右. 因此， 对于仅主体完工而仪器、 设备没有入驻的建筑结构， 当我们以其动力特性的分析结果与设计资料作对比分析时仍会产生一定的误差， 而这一误差对于高层及超高层建筑将更加明显.

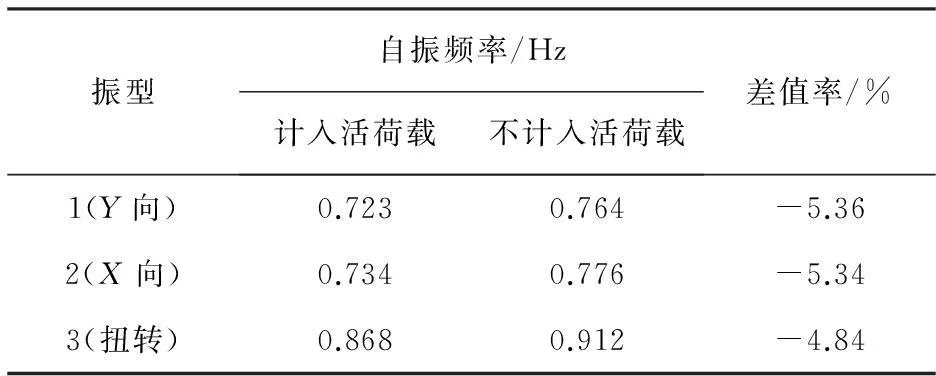
表 1　结构固有频率计算表

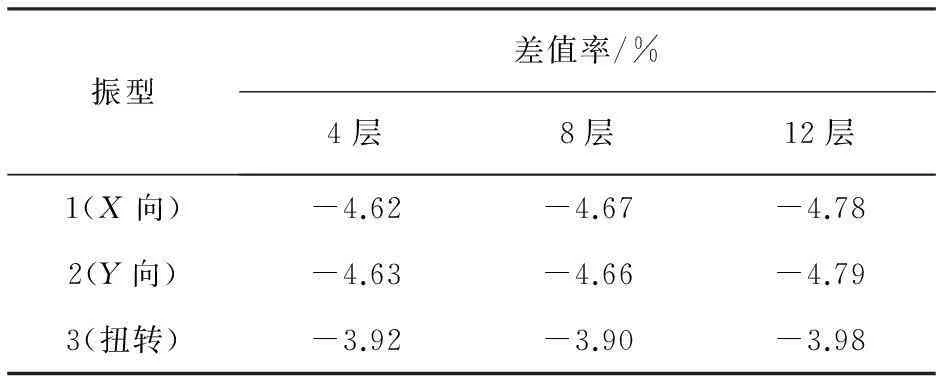
表 2　固有频率差值计算表

4结束语

通常而言， 进行结构设计时， 在结构模态质量矩阵中考虑组合值系数计入可变荷载的影响， 对结构体系承载力设计及抗震设计是有利的. 然而， 在进行后期结构整体的动力特性评定时， 忽略可变荷载的影响将会使当前结构体系的自振频率变小， 从而影响整体刚度的评定. 本文通过分析得出以下结论：

1) 对于高层混凝土框架结构， 可变荷载的计入对体系较低阶固有频率的影响在5%左右， 而这一影响对于高层及超高层结构体系将更加明显；

2) 对于钢结构体系而言， 由于其质量轻的特点[11]， 可变荷载的计入对体系固有频率的影响将更加显著；

3) 在评价结构体系整体刚度时若应用模态测试方法， 建议对于主体完工初期进行测试的高层及超高层结构体系， 需正确评估折算可变荷载对模态分析结果的影响， 以获得更加精确的分析结果.

参考文献：

[1]徐建. 建筑振动工程手册 [M]. 北京: 中国建筑工业出版社, 2002.

[2]周云.粘弹性阻尼减震结构设计[M]. 北京: 武汉理工大学出版社, 2006.

[3]GB50011-2010 建筑抗震设计规范[S]. 北京: 中国建筑工业出版社, 2010.

[4]张新培. 钢筋混凝土抗震结构非线性分析[M]. 北京: 科学出版社, 2003.

[5]刘晶波. 结构动力学[M]. 北京: 科学出版社, 2003.

[6]张相庭. 振动学基础[M]. 北京: 同济大学大学出版社, 1994.

[7]刘习军, 贾启芬. 工程振动理论与测试技术[M]. 北京: 高等教育出版社, 2004.

[8]JGJ3-2010 高层建筑混凝土结构技术规程[S]. 北京: 中国建筑工业出版社, 2010.

[9]陈志鹏, 宝志雯, 王宗纲. 京广中心大厦钢结构动力特性的测试与分析[J]. 钢结构, 1992(2): 36-39.

[10]GB50009-2012 建筑结构荷载规范[S]. 北京: 中国建筑工业出版社, 2012.

[11]陈绍蕃,顾强. 钢结构基础[M]. 北京: 中国建筑工业出版社, 2003.

Discussion on Modal Analysis and Evaluation with the Influence of Variable Load

GAO Hongjian1, LIU Kun2, GUO Jiao1

(1. College of Civil Engineering, Hebei University of Technology, Tianjin 300401, China;2. Planning Department, Hebei University of Technology, Tianjin 300401, China)

Abstract:Obtaining dynamic characteristics of structure by experiment, which can make further evaluation of the structure models. In order to evaluate the effect of variable load of building structures when included in mass matrix, the essay use the way of theoretical analysis and structure analysis by software modeling can evaluate the change of natural frequency of the structure when take variable load into consideration, which two aspects indicated that the results of analysis and evaluation of the calculation models would be more ideal when we considered the influence of variable loads on natural frequency of the structures and then globally evaluate structures for high-rise buildings and ultra-tall buildings.

Key words:variable load; structural modal analysis; dynamic characteristics test

中图分类号:TU312

文献标识码:A

doi:10.3969/j.issn.1671-7449.2016.01.011

作者简介：高洪健(1991-)， 男， 硕士生， 主要从事工程抗震设计和结构检测与加固的研究.

收稿日期:2015-08-30

文章编号:1671-7449(2016)01-0057-05