基于顾客选择的自提点选址双层规划模型
陈义友 张 锦 曾 倩 罗建强
(1. 西南交通大学交通运输与物流学院; 2. 江苏大学管理学院)
基于顾客选择的自提点选址双层规划模型
陈义友1张 锦1曾 倩1罗建强2
(1. 西南交通大学交通运输与物流学院; 2. 江苏大学管理学院)
顾客选择行为影响配送企业自提点网络的运作效率。运用前景理论和MNL模型,分别刻画顾客对送货上门存在的依赖心理和缺乏准确计算能力评估自提服务损失价值的有限理性行为。将配送服务模拟成不同的排队系统,重新构造送货上门服务和不同自提服务的期待价值函数。考虑配送企业和顾客的不同利益,构建自提点选址双层规划模型,以NSGA-II和免疫算法迭代求解上下层模型并进行算例分析。计算结果验证了模型和算法的有效性与可行性,揭示了配送企业在布局自提点时应关注顾客有限理性行为。
自提点选址; 顾客有限理性; 前景理论; MNL模型; 双层规划
自提服务增强了顾客的体验,降低了传统送货上门一次失败率和碳排放量[1],提高了配送企业的运作效率[2]。自提作为一种新兴服务,顾客是否完全接受,除了自提服务具有的优势外,还受到自提点是否出现拥堵[3, 4]、是否提供送货上门服务的影响[5]。顾客选择行为影响着配送企业布局自提点网络的运作效率[4]。
关于自提点选址的研究,WU等[6]考虑城市潜在顾客的分布位置及其取货方式,基于新加坡公共运输数据,采用核函数转换方法,重新定义顾客的配对位置,并采用K均值聚类方法,确定自提点的位置,但模型主要以距离最近进行选址,且假定顾客都是愿意选择自提服务。周翔等[7]考虑配送时长、取货距离和取货时间,以顾客满意度为优化目标,采用中心偏移二次聚类算法,求解电商企业末端节点的数量和位置,但模型没有考虑顾客的有限理性选择行为、不同自提点类型的影响。杨朋珏等[8]综合考虑送货上门和顾客自提两种配送模式,建立了基于效率性和便利性的双目标末端网点选址模型,并用遗传算法进行求解,但模型假定顾客选择送货上门与自提服务的比例为固定数值,没有考虑顾客到备选网点距离的长短对其产生的影响。张戎等[9]从规划者和客户两个角度出发,建立了城市末端节点的双层规划模型,基于反应函数设计了启发式算法,求解得到上海徐家汇街道的末端网点布局规划方案,模型的下层规划考虑了末端节点的服务距离、服务价格和服务质量三方面因素,但主要是以成本来衡量,没有考虑送货上门服务对顾客选择的影响,也忽略了顾客的有限理性行为。陈义友等[4]运用MNL模型,刻画了顾客到不同自提点接受服务的有限理性行为,考虑自提点的拥堵情形、顾客取货距离和自提点吸引力等因素,构建了基于顾客有限理性的自提点选址模型,但模型决策主体从顾客出发,没有考虑顾客对送货上门的依赖行为和自提点类型的多样化。
多项logit模型(multinomial logit model, MNL)已成为刻画顾客有限理性选择行为的一种重要方法[10]。SU[11]将MNL模型运用到报童模型中,解释了订货量大小受到有限理性决策者的影响,识别出系统偏差。ZHANG等[12]考虑顾客的随机选择行为,基于MNL模型建立了预防性医疗设施网络设计模型,模型考虑了预防性医疗设施的最小服务容量、顾客平均等待时间等因素,并用遗传算法和定位-分配算法进行求解。陈义友等[4]考虑顾客有限理性行为,基于MNL模型建立了自提点的选址模型,并用免疫算法、贪婪取走算法和上升算法进行求解。笔者在陈义友等[4]的研究基础上,考虑顾客有限理性行为,运用前景理论的价值函数,修正顾客选择不同自提点服务的效用,用改进的MNL模型,探讨基于顾客选择的自提点选址双层规划问题。
本研究的自提点选址问题主要贡献体现在:①提出顾客选择自提服务时存在依赖心理,且无法准确评估自提服务损失价值的有限理性行为;②考虑自提点的类型,改进现有MNL模型无法解决顾客存在上门依赖心理的行为选址问题;③综合考虑顾客和企业两个决策主体,建立了自提点选址的双层规划模型,并设计相应的算法求解。
1 顾客选择行为分析
实证研究和仿真实验证实决策者是有限理性人[10],存在参考依赖[13]、公平关切[14, 15]、决策偏差[3, 4]等行为。顾客在选择自提服务时是否也同样存在有限理性行为?自提点处理容量有限,顾客不清楚自提点是否出现拥堵,其包裹是否存在被拒绝的情形,顾客无法轻易地选择最优自提服务。此外,外部环境的不确定性,增加了顾客的选择难度。对此,顾客表现出有限理性行为[3, 4],缺乏准确的计算能力去评估自提服务的损失效用。这里采用MNL模型来刻画顾客随机选择行为,即每个顾客是以一定的概率接受自提点的服务,选择概率与目标自提点提供的效用成比例。关于MNL模型在行为选址方面的研究可参考陈义友等[4]及ZHANG等[12]的研究。
徐俊杰等[5]基于服务驱动假说,验证了送货上门服务缺陷对顾客自提服务选择有直接的促进作用。这说明顾客选择自提点的服务是受到送货上门服务的影响,对送货上门存在依赖心理。本研究以顾客选择送货上门的效用为参考点,运用前景理论的价值函数来描述顾客在有限理性条件下,选择到不同自提点接受服务的效用感知满意度。
假设所有顾客选择送货上门的价值一样,为V0,且V0>0,则顾客i选择送货上门的价值函数为
(1)
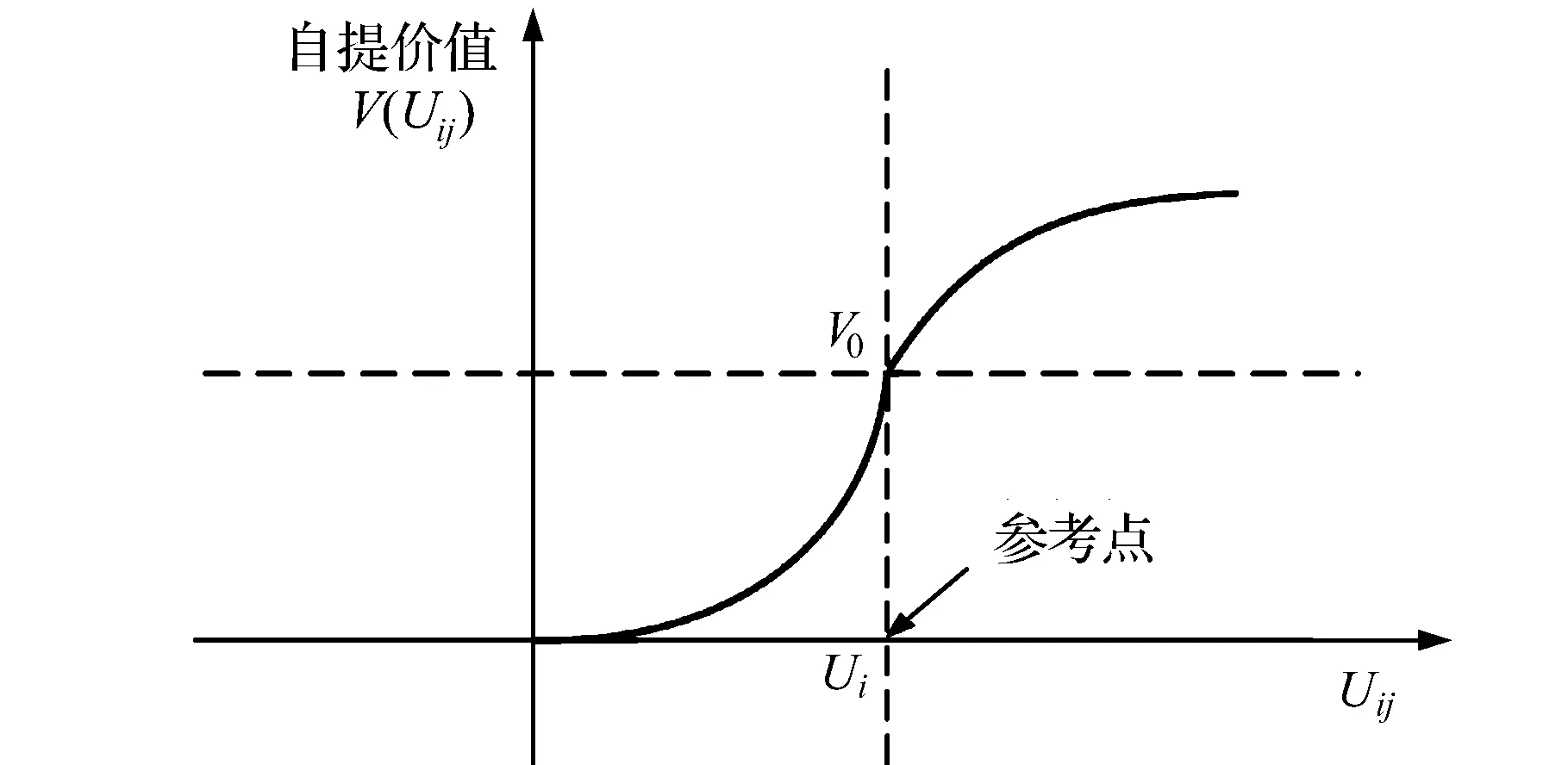
图1 顾客自提价值函数曲线
根据KAHNEMAN等[13]的研究,顾客i选择到自提点j接受服务的价值函数曲线见图1,计算公式为
(2)
式中,Uij表示顾客i选择自提点j的效用;Ui表示顾客i选择送货上门服务的效用,为顾客选择自提决策具有的参考点;λ表示对损失的规避程度(λ≥1);α和β分别表示收益与损失区间的风险偏好水平(0<α,β<1)。
2 自提点选址双层规划模型
2.1 模型假设
给出以下模型假设:①根据运行特征,自提点可分为有人值守型和无人值守型两种[16],本研究只考虑这两种类型;②顾客选择配送服务的唯一依据是基于配送服务价值最大化,且送货上门的价值为常数;③当顾客包裹派送到自提点被拒绝时,由配送企业选用送货上门的方式进行派送。
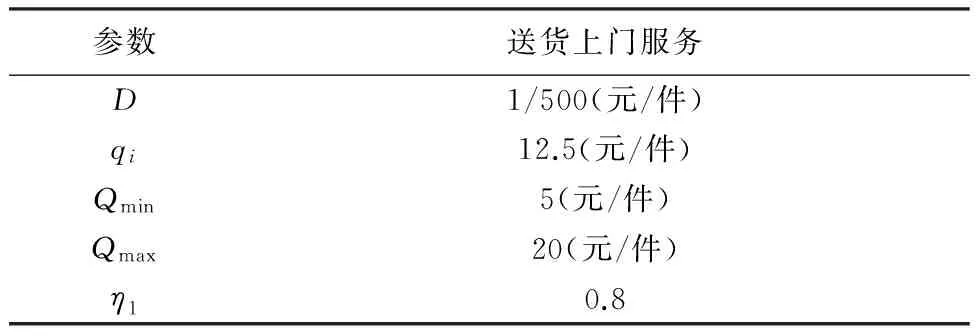
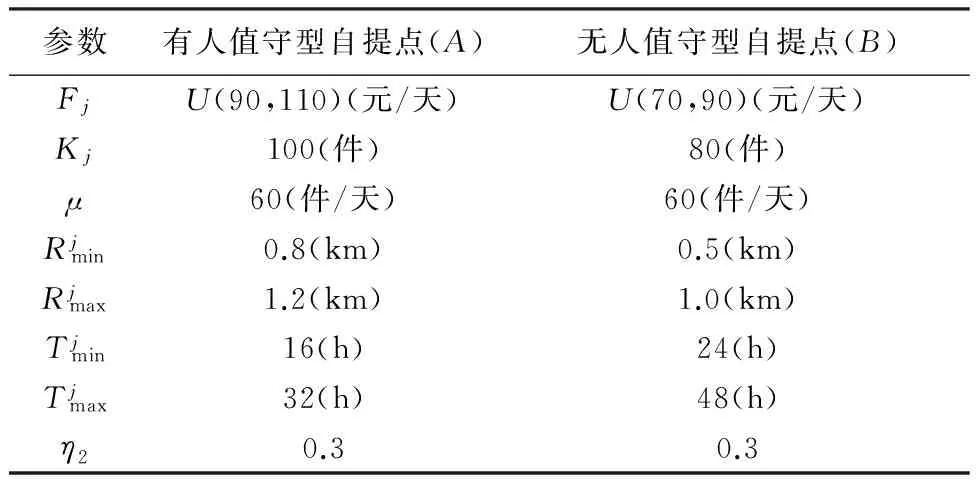
2.2 参数说明
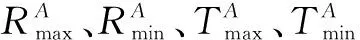
2.3 价值函数
2.3.1 送货上门价值函数
送货上门可描述为M/D/1的排队系统,遵循FIFO原则。顾客单位时间需求服从泊松分布λi,其中,D是企业配送单位包裹到顾客手中所花费的时间。
如果顾客i以概率pi选择送货上门服务,基于M/D/1模型,顾客选择送货上门服务的平均等待时间为
(3)
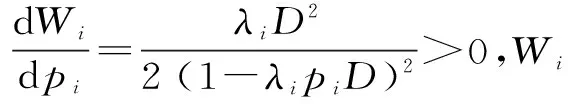
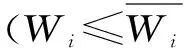
(4)
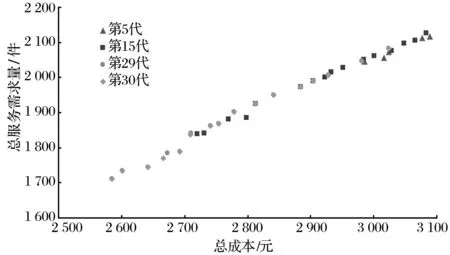
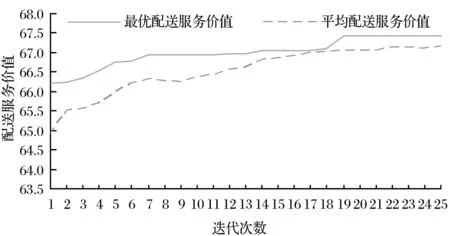
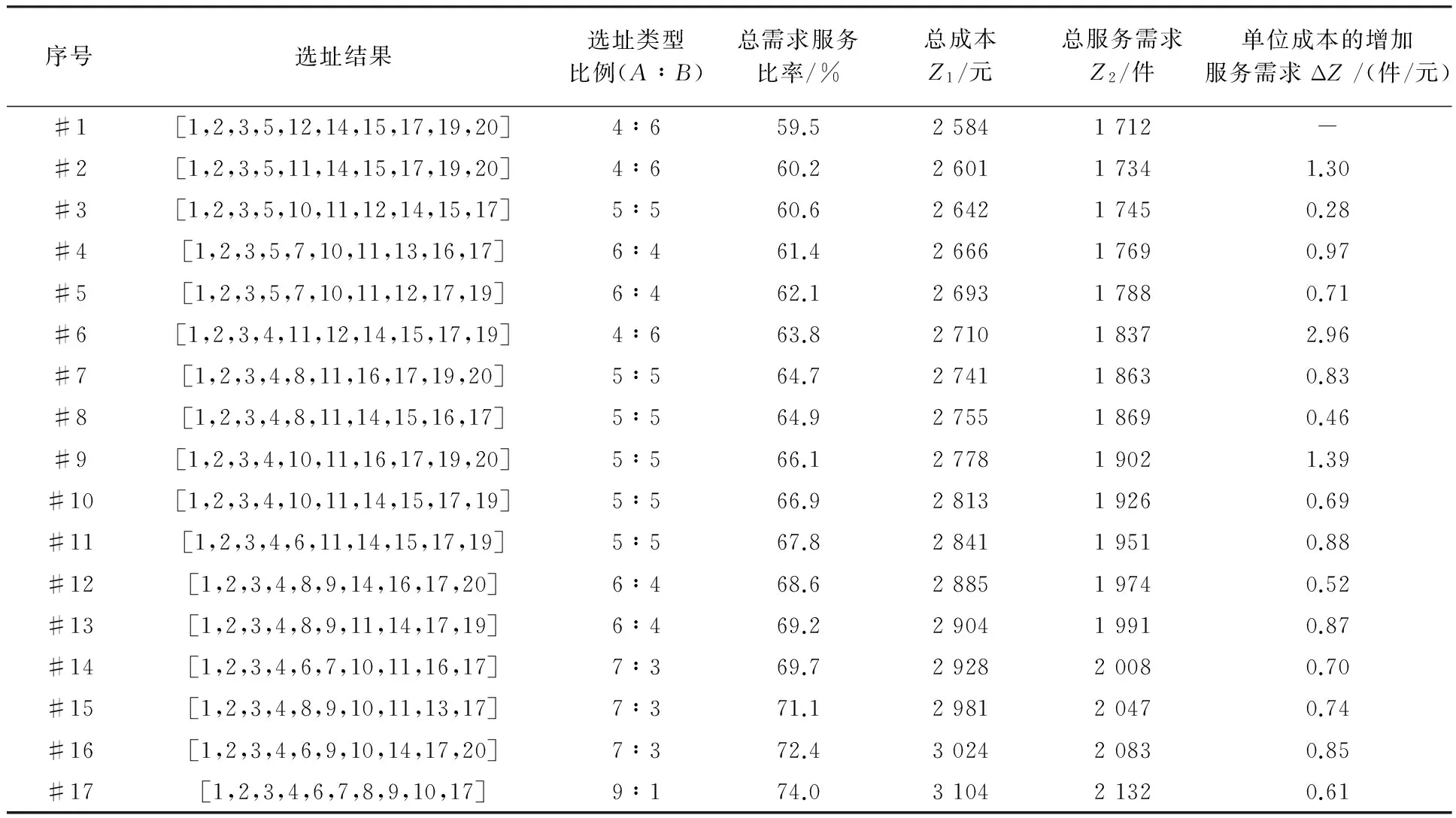
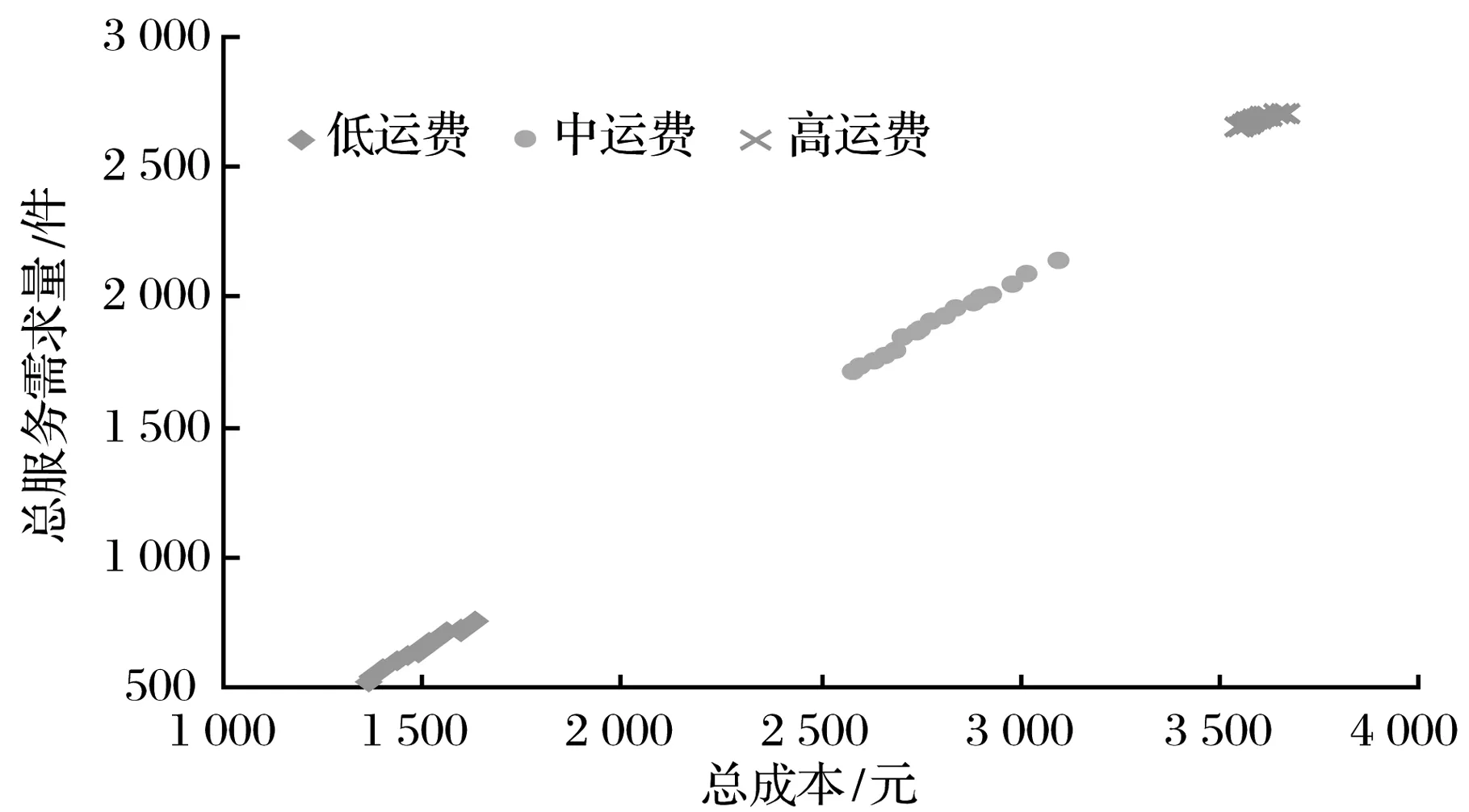
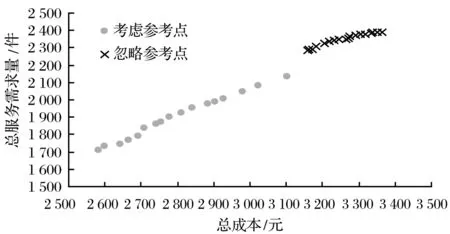
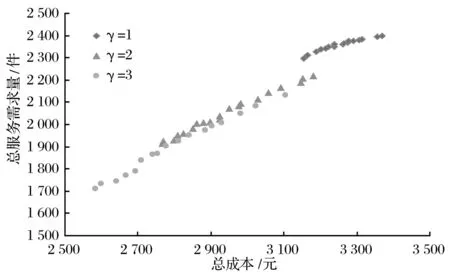
如果顾客i选择送货上门的服务,则需要支付一定的运费qi。假设当运费qi在顾客可接受的范围内(qi≤Qmin),运费对顾客的效用f(qi)为1;超过一定的范围(qi≥Qmax),f(qi)为0;在两者之间(Qmin (5) 考虑平均等待时间对顾客选择送货上门服务效用Ui的影响,则有 (6) 式中,η1表示顾客支付运费的效用权重。 由于假设不同顾客送货上门的价值为常数,故顾客i选择送货上门的价值为 (7) 2.3.2 自提价值函数 自提点可描述为M/M/K/K的排队系统,其中K是自提点的处理容量。假设顾客单位时间需求服从泊松分布λi。每个包裹存储的时间(或者存储的空间)服从负指数分布,假设所有类型的包裹的存储时间是相等的,均为1/μ,包裹间的存储时间是独立分布的。 如果顾客i以概率pij选择自提点j的服务,自提点处理容量为Kj,基于Erlang-B模型,当自提点容量超过负荷,自提点j顾客包裹被转移的概率Pjloss为 (8) 其中 (9) (10) 式(9)中,ρj为自提点j的服务强度;式(10)中,λj为顾客到自提点j的需求率。 杨聚平等[17]通过调查数据得出,对于自提服务的功能需求,有60.2%的顾客选择无取货时间限制且取货距离较短;对于取货时间的要求,有51.97%的顾客选择7×24的取货时间。由此,本研究将顾客取货距离和取货时间作为对顾客选择自提服务的主要影响因素;同时,考虑自提点对顾客的吸引力,定义顾客选择自提服务的效用函数。 对于取货距离,顾客大多是步行到自提点进行取货。当取货距离在一定范围内,距离越近,顾客效用越大;而超过一定的范围时,取货距离对顾客效用为0。为描述这种现象,采用线性递减函数来定义顾客i到自提点j的取货距离效用函数,即 (11) 对于取货时间,在一定范围内,取货时间越长,顾客的效用越大;而小于一定的范围,取货时间对顾客的效用为0。采用线性递增函数来定义顾客i到自提点j取货时间的效用函数为 (12) 考虑自提点的吸引力和顾客包裹被转移的概率,顾客i选择不同自提点服务的效用函数为 (13) 式中,η2表示顾客取货距离效用权重,Aij表示自提点i对顾客j的吸引力,且Aij∈[0,1]。此时,顾客i选择接受自提点j的价值函数为 (14) 2.4 模型建立 基于MNL模型,顾客i到自提点j取货的概率为 (15) 同理,顾客i选择送货上门的概率为 (16) 式(15)和式(16)中的γ可理解为顾客选择接受自提和送货上门服务的理性程度。当γ→0时,顾客处于非理性条件下,无法辨别出每种配送服务的区别,按照相同的概率随机选择接受服务;当γ→∞时,顾客选择接受完全理性下的最优配送服务。 自提点选址问题涉及到顾客和配送企业两个利益主体,双层规划模型能从企业和顾客两个角度出发,在优化配送企业整个自提服务系统的同时,使得顾客的价值最大化,更能确实反映实际问题。由此,可得基于顾客选择的自提点选址双层规划模型。上层模型U为 (17) (18) st:式(3)~式(16)和 (19) (20) (21) (22) 上层是企业做决策,式(17)表示配送企业设立自提点的单位时间总成本最小,其中,第1项表示设立自提点单位时间的固定成本,第2项和第3项分别表示单位时间自提服务配送员和送货上门服务配送员的工资,即为配送成本;式(18)表示设立的自提点单位时间内服务的需求最大;式(19)表示顾客的实际自提总量;式(20)表示顾客选择自提服务被拒绝,转而由配送员进行送货上门的配送总量;式(21)表示配送企业设立自提点的个数限制;式(22)为决策变量约束。 下层模型L为 (23) st:式(3)~式(16)。 下层是顾客做决策,式(23)表示所有顾客选择最后一公里配送服务总价值最大,第1项表示顾客选择自提服务的总价值,第2项表示顾客选择送货上门服务的总价值。 双层规划模型求解属于NP-hard问题,不存在多项式求解算法。本研究采用双层迭代法进行计算[18],具体步骤如下。 步骤1 令迭代次数gen=1。 上层模型是多目标优化问题,求解多目标约束优化的进化算法中,NSGA-II是较为成熟的求解算法[18, 19]。为了运用此算法,结合自提点选址模型的特性,本研究设计新的编码方式和遗传算子。具体步骤如下。 (1) 编码及初始种群产生 采用整数编码的形式,在可行域内随机产生UN个个体,构成初始种群。每个个体的长度为p,个体的基因位代表被选为备选自提点的序号。 (2) 适应度计算 根据选址方案,分别求解出两个目标函数的适应度。令F1=Z1,F2=1/Z2。 (3) 快速非支配排序 令个体i的两个适应度分别为Fi,1和Fi,2。若个体i支配个体j,则需要满足条件:Fi,1≤Fj,1且Fi,2≤Fj,2。依据此定义,首先将当前种群中所有非劣解个体划分为同一个等级,记为ranki;然后从种群中剔除已分配好等级的个体,对剩余个体进行非支配排序,记为ranki+1;反复重复此过程,最后直至种群中所有个体都被分级完成。 (4) 拥挤距离计算 将排序等级相同的个体按照F1和F2升序排列。对于每个等级排在边缘的个体,为了使其具有选择优势,令它们的拥挤距离为INF(INF为一个无穷大的正数)。而对每个等级排在中间的个体,按照式(24)求解个体i的拥挤距离ci,得 (24) (5) 选择操作 基于步骤2中式(3)和式(4)的计算结果,采用锦标赛选择算子,从种群中选出UN/2个个体,组成新种群。具体选择过程为:从种群中随机选择两个个体,若ranki (6) 交叉操作 依据交叉概率pc,采用单点交叉法进行交叉操作。交叉完产生的新个体有相同的序号,剔除相同的序号,然后再随机产生新序号,使新个体的长度等于p。 (7) 变异操作 依据变异概率pm,采用单点变异法进行变异操作。随机采用[1,m]之间的整数替换变异个体的基因,变异过程中需确保个体的基因值互不相同,其中m表示备选自提点的总数。 (8) 精英策略 合并父代种群Pgen和子代种群Qgen,形成新的种群Rgen=Pgen∪Qgen,Rgen的个体数为1.5UN。接着跳转到步骤2中式(2)~式(4),依次进行个体的适应度计算、快速非支配排序、拥挤距离计算,依据等级到高低和拥挤距离大小逐一选择个体,直到选出UN个个体,构成新的种群Pgen+1。 免疫算法是一种模拟生物种群进化策略的随机搜索算法,广泛应用于基站等工程领域问题中[20, 21]。本研究尝试将免疫算法运用到自提点选址下层模型中,具体步骤如下[4]。 (1) 产生初始种群 编码及种群产生方法与上层模型U类似,产生LN个个体。 (3) 产生记忆细胞 记忆库的抗体数用δ表示。采取精英保留策略,记精英抗体数为ϑ。每次产生记忆细胞时,将与抗原亲和度高的前ϑ个抗体存入记忆库,然后从剩余抗体中选择个体期望繁殖概率高的前(δ-ϑ)个抗体存入记忆库。 (4) 形成父代群体 父代群体数用(LN-δ)表示。采用记忆细胞产生的方法来形成父代群体。借鉴遗传算法的进化算子,对形成的父代群体进行选择、交叉和变异操作。 (5) 产生新抗体群 将产生的记忆细胞和形成的父代群体合并产生新抗体群。 (6) 判断程序终止条件 如果迭代次数达到预先规定的最大进化代数LGEN,则终止条件。 陈义友等[4]研究了考虑顾客有限理性的自提点选址问题,但其中的算例以有人值守型自提点为例,仅考虑顾客取货距离和自提点吸引力两个因素,无法作为自提点选址的标准算例。为验证构建模型与算法的有效性,在此算例基础上,结合实际调研,设计一个新的算例进行仿真模拟。 4.1 参数设置 假设某区域中顾客数n=30,有人值守型自提点数nA=10,无人值守型自提点数nB=10,配送企业设立的自提点数p=10。顾客初始需求服从参数λi=100(件/天)的泊松分布,如果产生的需求为0,则令其值为100。顾客到备选自提点取货距离rij按照正态分布N(1.0,0.82)的密度随机产生。如果产生的随机数小于0,则将其改为1.0,每单位距离为1 km。tj服从参数为t=16(h)的负指数分布,如果参数的取货时间为0,则令其值为16。不同自提点对顾客的吸引力Aij服从均匀分布U(0.85,1)。送货上门配送员日均配送量v2=100(件/天),日均工资w2=150(元/天);自提配送员日均配送量v1=250(件/天),日均工资w1=250(元/天)。为了分析不同运费对自提点选址的影响,令qi=(Qmin+Qmax)/2。由TVERSKY等[22]的分析可知,α=β=0.88,λ=2.25。为使得V(Uij)≥0,令V0=2.25。假设顾客具有较高的理性程度,结合仿真数据,令顾客理性程度γ=3。其他参数分别见表1和表2。 表1 送货上门参数设置 表2 不同类型自提点参数设置 4.2 计算结果 在Xntel(R) Xeon(R) E5645@2.40 GHz CPU,16GB内存的电脑上,利用MATLAB R2014a软件运行计算。经过多次测试,确定算法参数设置如下:上层模型NSGA-II种群的规模均为UN=20,上层最大进化代数UGEN=30,求解精度ε=5%。下层模型免疫算法抗体总规模LN=20,记忆库容量δ=5,精英抗体数ϑ=2,抗体间亲和力阀值T=0.7,多样性评价参数α=0.9,下层最大迭代次数LGEN=25。上下层算法的交叉概率均为pc=0.9,变异概率为pm=0.05。 上层模型不同代的非支配解见图2。由图2可知,随着进化代数的增加,得到的解不断逼近Pareto前沿。下层模型解的变化见图3。这表明设计的算法具有较高的收敛性。 图2 上层模型不同代的非支配解 图3 下层模型解的变化 Pareto最优解的具体信息见表3。由图2和表3可得到以下结论:①自提点总服务需求随着自提点总成本的增加而增加。从投入产出的角度看,企业可选择单位成本增加的服务需求最大的选址方案。 本算例中, 企业可选择方案#6。②总体上看,当企业设立的有人值守型自提点数不小于无人值守型自提点数时,设立的自提点能满足更多的需求。表明在该区域中,有人值守型自提点相比无人值守型自提点,更受顾客喜爱。③各个Pareto最优解的自提点总需求服务比例在59.5%~74.0%之间。换言之,区域中有26%~40.5%左右的顾客选择送货上门服务。理由在于:一方面,顾客支付运费适中,相对一些自提点的服务,送货上门服务具有较大的优势(顾客不同支付运费对Pareto最优解的影响见图4);另一方面,顾客选择自提点服务时存在有限理性行为,受到送货上门参考点和顾客理性程度的影响(见图5和图6)。由此,并非所有顾客选择自提服务,而存在部分顾客选择送货上门服务。 为测试不同顾客数n和企业需设立的自提点数p对Pareto最优解的影响,令n=30,40,50;p=6,10,12。根据相关计算参数,并调整双层迭代法计算参数,每组算例运算5次,计算结果见表4。 表3 Pareto最优解 图4 不同顾客支付运费的非支配 图5 参考点影响的非支配 图6 不同顾客理性程度的非支配解 由表4可知,随着设立自提点个数p的增加,平均需求服务比率也相应增加,平均单位成本服务需求量则随之减少;随着顾客数n的增加,平均需求服务比率和平均单位成本服务需求量均有所增加。从运算时间看,随着顾客数和设立自提点数的增加,设计的迭代算法求解时间也随之增加。本研究模型相比其他同类型的多目标选址模型计算时间偏长,主要原因在于适应度函数需要通过计算Pjloss和pij两个关键参数得到,而Pjloss和pij互相影响,需要循环反复迭代,才能得到最终的“均衡解”。由此可知,设计的双层迭代法计算较为困难,运算耗时较长。 表4 不同规模算例求解结果比较 4.3 敏感性分析 (1)参考点的影响 假设顾客选择配送服务时,不考虑送货上门参考点的影响,即顾客决策是遵循配送服务效用最大化。以效用函数代替价值函数,重新构造下层规划的目标函数及选择概率函数,得到的非支配解见图5。总体上看,忽略送货上门参考点的影响,将导致各个Pareto最优解总成本和总服务需求量都大于考虑参考点影响的情形,但其单位成本增加的服务需求小于考虑参考点影响的情形。如果顾客选择自提服务时不存在送货上门依赖的心理,则配送企业可投入较多的资金去满足顾客需求,但单位成本增加的服务需求量较小;反之,配送企业投入的资金较少,服务的需求也较少,但单位成本增加的服务需求量较大。 (2)顾客理性程度的影响 为分析顾客的不同理性程度,结合仿真数据,令γ∈{1,2,3},分别代表实际生活中顾客的主要类型。不同顾客理性程度的非支配解见图6。当顾客理性程度增加时,自提点总成本与总服务需求量都减少,但单位成本增加的服务需求量随之增大。配送企业应充分调研分析顾客的理性程度,以便确定最优的选址方案。 (3)顾客支付运费的影响 为分析顾客不同支付费用对最优解的影响,令qi∈{Qmin,(Qmin+Qmax)/2,Qmax},即qi∈{5,12.5,20},分别代表不同大小的运费。不同顾客支付运费的非支配解见图4。当顾客支付运费增加时,自提点总成本与总服务需求量也随之增加,但单位成本增加的服务需求量随之减少。若配送企业的运费设置过高,顾客将更多选择自提服务。企业应合理设置运费,以扩大末端配送市场份额。 针对顾客在选择自提服务时,存在对送货上门存在依赖心理,且无法准确评估自提服务的损失价值的有限理性行为,构建了自提点选址双层规划模型。模型的特点表现在:①刻画了顾客选择自提服务的有限理性行为,拓展了前景理论和MNL模型在物流设施选址的应用;②采用自下而上的逻辑布局自提点,在决策过程中考虑了顾客选择行为的影响,有利于配送企业科学合理配置末端物流资源。需要指出的是,本研究没有考虑竞争企业自提点的影响,这将是下一步需要探讨的研究方向。 [1]SONGL,GUANW,CHERRETTT,etal.QuantifyingtheGreenhouseGasEmissionsofLocalCollection-and-DeliveryPointsforLast-MileDeliveries[J].TransportationResearchRecord:JournaloftheTransportationResearchBoard, 2013,2 340:66~73 [2]WANGX,ZHANL,RUANJ,etal.HowtoChoose“LastMile”DeliveryModesforE-Fulfillment[J/OL].MathematicalProblemsinEngineering,2014,2014:1~11[2016-02-20].http://dx.doi.org/10.1155/2014/417129 [3]HAYELY,QUADRID,JIMÉNEZT,etal.DecentralizedOptimizationofLast-MileDeliveryServiceswithNon-CooperativeBoundedRationalCustomers[J].AnnalsofOperationsResearch, 2016,239(2):451~469 [4] 陈义友, 张锦, 陈以衡, 等. 基于顾客有限理性的自提点选址研究[J]. 工业工程与管理, 2015,20(6):92~100 [5] 徐俊杰, 姜凌, 李亦亮. 基于服务驱动假说的消费者自提包裹选择意愿研究[J]. 管理学报, 2014,11(12):1 850~1 857 [6]WUH,SHAOD,NGWS.LocatingSelf-CollectionPointsforLast-MileLogisticsUsingPublicTransportData[M]//CAOT,LIME,ZHOUZ,etal.AdvancesinKnowledgeDiscoveryandDataMining.Berlin:SpringerInternationalPublishing, 2015:498~510 [7] 周翔, 许茂增, 吕奇光.B2C模式下配送中心与末端节点的两阶段布局优化模型[J]. 计算机集成制造系统, 2014,20(12):3 140~3 149 [8] 杨朋珏, 胡昊, 王俊嘉, 等. 电子商务环境下城市配送末端网点选址模型研究[J]. 工业工程与管理, 2014,19(1):35~40 [9] 张戎, 王镇豪. 城市配送末端节点布局双层规划模型及算法[J]. 同济大学学报:自然科学版, 2012,40(7):1 035~1 040 [10] 牟博佼, 李岩, 朱岩. 基于有限理性假设的运营管理研究现状及发展趋势[J]. 清华大学学报:自然科学版, 2012,52(2):253~259 [11]SUX.BoundedRationalityinNewsvendorModels[J].ManufacturingandServiceOperationsManagement, 2008,10(4):566~589 [12]ZHANGY,BERMANO,VERTERV.TheImpactofClientChoiceonPreventiveHealthcareFacilityNetworkDesign[J].ORSpectrum, 2012,34(2):349~370 [13]KAHNEMAND,TVERSKYA.ProspectTheory:AnAnalysisofDecisionunderRisk[J].Econometrica:JournaloftheEconometricSociety, 1979,47(2):263~291 [14] 陈章跃, 王勇, 陈晓旭. 制造商双向公平关切下闭环供应链的竞争分析[J]. 管理学报, 2016,13(5):772~780 [15] 马鹏, 曹杰. 公平偏好行为下制造商质量投资策略及供应链绩效研究[J]. 管理学报, 2016,13(6):922~928 [16]WELTEVREDENJW.B2CE-EommerceLogistics:TheRiseofCollection-and-DeliveryPointsintheNetherlands[J].InternationalJournalofRetailandDistributionManagement, 2008,36(8):638~660 [17] 杨聚平, 杨长春, 姚宣霞. 电子商务物流中的间接配送模式研究[J]. 商业研究, 2014(5):162~171 [18] 韩霜, 张邻, 谭智华, 等. 动态竞争环境下的物流配送中心双层规划模型[J]. 控制与决策, 2014,29(11):2 055~2 060 [19]DEBK,PRATAPA,AGARWALS,etal.AFastandElitistMultiobjectiveGeneticAlgorithm:NSGA-II[J].IEEETransactionsonEvolutionaryComputation, 2002,6(2):182~197 [20] 张英杰, 毛赐平, 俎云霄, 等. 基于免疫算法的TD-SCDMA网络基站选址优化[J]. 通信学报, 2014,35(5):44~48 [21] 朱思峰, 陈国强, 张新刚, 等. 多目标优化量子免疫算法求解基站选址问题[J]. 华中科技大学学报:自然科学版, 2012,40(1):49~53 [22]TVERSKYA,KAHNEMAND.AdvancesinProspectTheory:CumulativeRepresentationofUncertainty[J].JournalofRiskandUncertainty, 1992,5(4):297~323 (编辑 桂林) Bi-Level Optimization Model for Pickup Point Location under Customer Choices CHEN Yiyou1ZHANG Jin1ZENG Qian1LUO Jianqiang2 (1. Southwest Jiaotong University, Chengdu, China;2. Jiangsu University, Zhenjiang, Jiangsu, China) Customer choice behavior affects the operational efficiency of distribution enterprises’ pickup point network. Customers have reference dependence behavior in the home delivery service and are lack of accurate calculation capability to assess loss value of pick-up service. Customers bounded rationality is depicted by prospect theory and MNL model. The home delivery service and pickup points are simulated as different queueing system and the functions of customers’ expected value under different situations are constructed. Taking the distribution enterprises’ and customers’ different benefits into account, a bi-level optimization model for pickup point location is proposed. Furthermore, an iteration algorithm is designed to solve the upper and lower model based on NSGA-II and immune algorithm, and a numerical example is presented as an illustration. The results verify the validity and feasibility of the model and the algorithm, and show that distribution enterprises should pay attention to customers bounded rationality when layouting pickup points. pickup point location; customers bounded rationality; prospect theory; MNL model; bi-level optimization 10.3969/j.issn.1672-884x.2016.12.013 2016-03-07 国家自然科学基金资助项目(71472077,41501123);中央高校基本科研业务费专项资金资助项目(2682016CX058) C93 A 1672-884X(2016)12-1842-09 张锦(1963~),男,四川广元人。西南交通大学(成都市 610031)交通运输与物流学院教授、博士研究生导师,博士。研究方向为物流系统规划。E-mail:zhjswjtu@swjtu.edu.cn
3 算法设计
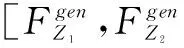
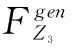
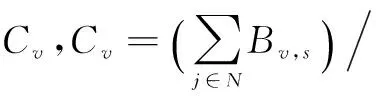
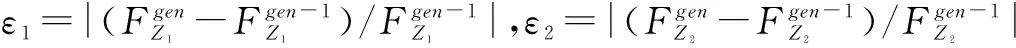
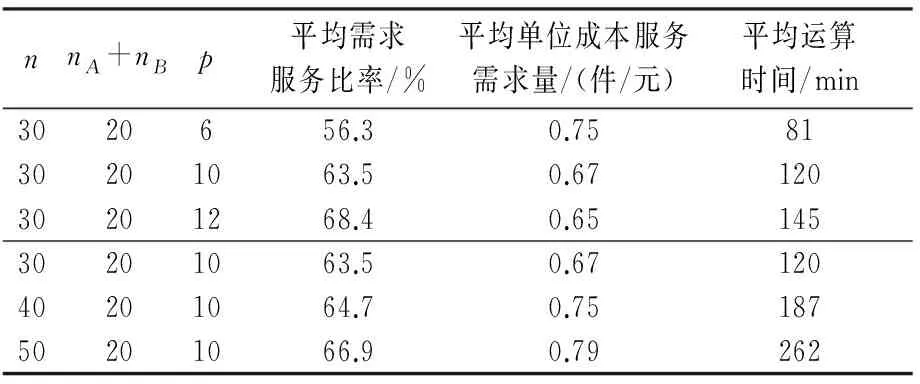
4 算例分析
5 结语

