考虑供应断裂与产能恢复的多供应商-单制造商采购策略研究
戴 宾 范 雷 田 颖
(武汉大学经济与管理学院)
考虑供应断裂与产能恢复的多供应商-单制造商采购策略研究
戴 宾 范 雷 田 颖
(武汉大学经济与管理学院)
针对多供应商-单制造商的供应链模型,同时考虑供应断裂与产能恢复,在价格外生条件下建立一个采购联合优化模型来研究制造商的采购策略,分析供应商的产能恢复决策。研究表明,不可靠供应商的最优订单按照成本优势与供应风险比率排序,且与市场大小无关;入选的不可靠供应商可以通过改进其自身产能恢复比率来增大其订货量,但同时制造商的总订货量、可靠供应商的订货量和其他未投资产能恢复的不可靠供应商的订货量均减小。供应商的产能恢复投资决策表明,只有当供应商的固定投资成本足够小,或者制造商的采购价格足够大时,不可靠供应商才会投资产能恢复。
供应断裂; 产能恢复; 多源采购; 采购策略
1 研究背景
近年来,随着国际分工合作以及精益化生产思想的不断发展,企业在全球化进程中不断增加对供应链构造的投入,供应链表现出更加高效且低成本的性质。然而,面对环境中的各种不确定性因素,企业投入大量精力打造的全球化供应链又显现出脆弱的一面。因遭遇突发事件而导致的供应断裂,常常让制造商们措手不及,甚至丧失市场机会。如2000年,美国新墨西哥州飞利浦公司第22号芯片厂发生火灾,Ericsson公司因此损失了4亿美元的销售额,市场占有率也从原来的12%下降为9%[1]。2008年底,国际金融危机造成我国广东大量工厂停业或者倒闭,使得以这些工厂生产的产品或零部件为原材料的下游制造商无法顺利生产,甚至倒闭。2007年,加拿大的铁路工人举行了一个星期的罢工,导致大量重要原材料的缺乏,从而影响了北美的多个市场[2]。2011年,利比亚的武装暴动导致多数原油供应的中断[3]。可能导致供应断裂的其他突发事件有停电、恐怖袭击等。同时,劳资争议、政局不稳、自然灾害等因素加大了企业面临供应断裂的风险,这种风险不同于生产中的不确定性风险,具有很强的破坏性[4]。这些突发事件不仅给供应商本身带来了巨大的损失,同时也给供应链下游企业带来了严重的后果。这警醒人们对供应保障问题的研究,考虑供应断裂的采购问题已成为许多学者关注的重点。
为避免供应断裂带来严重后果,许多公司采取多源采购战略,即同时向两个或两个以上的供应商采购。在部分供应商能保证供应的条件下,多源采购是应对供应风险的一个切实可行的方法[5]。在供应风险管理研究中,普遍存在对可靠供应商的假设。学者们提倡在供应商名单中加入可靠供应商,作为管理供应断裂的一种手段。HEYES[6]认为,保障供应的一种方法就是通过与可靠供应商合作,来保证在某一采购周期内的最小供应量。HU等[7]发现,通过对不可靠供应商的成本优势与供应风险比率进行排序,可确定供应商的选择标准与采购数量。HU等[8]基于存在产能恢复的前提,探讨了制造商如何通过激励机制降低供应断裂风险带来的损失。此外,也可以在突发事件后通过相应的应急处理措施(如产能恢复)来控制损失。然而,并不是所有的供应断裂都可以进行产能恢复,如2011年的日本大地震。本研究主要讨论可以进行产能恢复的供应断裂情况,如经济危机、罢工等;不能进行产能恢复的情况可以视为产能恢复比率为零时的一种特殊情况。本研究针对多供应商-单制造商的供应链网络模型,同时考虑供应断裂与产能恢复因素,以制造商利润最大化为目标,建立一个采购联合优化模型来研究制造商的采购策略,同时对供应商的产能恢复决策进行分析。
2 文献综述
供应商可靠性及其对供应链管理的影响在过去的几十年中吸引了许多学者的关注。国外早期文献中,关于供应风险的研究专注于单一供应商的问题,由于没有可替换的来源,库存缓和战略是此类研究唯一的风险管理战略[8,9]。BIELECKI等[10]研究了不确定制造系统中的零库存策略。GURNANI等[11]、DADA等[12]及TOMLIN等[13]探讨供应不确定条件下的供应商多源化问题。TANG[14]在对供应风险进行表述时认为,应对供应风险控制,在战略上,取决于对供应网络的设计;在战术上,取决于对供应商的选择、供应商订单分配与供应合同的制定。HU等[7]研究了当供应商存在供应断裂风险时制造商的最优多源采购策略,并运用近似模型,发现最优不可靠供应商订单会按照成本优势与供应风险比率进行排序。HE等[15]对比了价格竞争下的紧急采购策略和订单分配采购策略。XU等[16]研究了需求和生产断裂下的最优生产库存模型。GIRI等[17]研究了需求和供应断裂下的合约设计问题来协调供应链。GUPTA等[18]研究了供应断裂和价格竞争下的联合采购问题。HU等[8]研究了制造商如何通过激励机制促使供应商投资产能恢复,分别在产能恢复增强战略和多源采购战略下,分析供应商的产能恢复决策。
肖勇波等[19]提出,在一个未来需求和组装产能同时具有不确定性的单周期面向订单装配系统中,实际需求信息的获取会影响制造商的最优库存决策和最优生产决策。温源等[20]研究了一个制造商向两个供应商进行联合采购的最优决策问题,认为多源采购是制造商降低供应风险的有效手段之一。马士华等[21]研究了供应不确定条件下,两供应商-单制造商系统在溢出库存惩罚下的风险共享协同模型,发现在溢出库存惩罚下,供应商和供应商、供应商和制造商之间存在纳什均衡。何青等[22]研究了供应商可以通过努力,同时改善供应可靠性和降低生产成本时的供应渠道决策问题。徐和等[23]研究了供应风险环境下,采购策略对制造商的产品价格和质量竞争的影响。朱传波等[24]同时考虑供应断裂与产能恢复因素,研究了制造商风险规避程度对供应链最优产能恢复比率的影响。
目前,相关的运作管理理论有以下研究方向:①通过运营和财务战略来减轻供应断裂带来的影响;②制定能够提高供应商可靠性的战略。学者们已经找出同供应风险相关的因素,如供应商之间的竞争、买方企业之间的竞争、价格与库存管理等。在类别①中,DONG等[25]研究了供应断裂管理中的财务缓和战略、运作缓和战略及应急战略。相较于本研究,他们只探讨了制造商向任一供应商做最优采购决策时所具有的特质,并分析了制造商针对可靠和不可靠供应商采取的不同的缓和战略。研究表明,除了投资库存和应急供应,购买商业中断保险也是一个可以降低供应不确定性影响的方法,并指出保险和特定的运作手段不总是替代关系,它同时也为产能恢复创造了条件。在类别②中,HU等[8]从战略设计角度探讨了降低供应风险的方法,学者们将研究重点转向制造商如何激励供应商投资产能恢复,使得在发生供应断裂时,供应商仍然能够恢复部分产能,以降低制造商的损失。
已有的研究在考虑供应风险时,重点放在了制造商库存战略上,较少考虑到通过优化订单分配模型来降低供应风险;同时,针对制造商激励策略的研究过于单一,大多仅考虑了激励因素对供应商产能恢复的影响,没有充分站在供应商的角度研究问题。笔者在HU等[7]、HU等[8]的研究基础上,针对多供应商-单制造商的供应链网络模型,综合供应断裂与产能恢复两种影响因素,研究其对制造商最优采购策略和供应商产能恢复决策的影响。即不可靠供应商S存在一定的概率γ发生供应断裂,同时,供应商能够在断裂发生后恢复比率yi的供应量,此时,该如何向可靠和不可靠供应商分配订单,使得制造商利润最大化;同时,供应商又该如何决策产能恢复比率,使得自身利润最大化。
本研究建立了一个采购联合优化模型,给出供应断裂下的制造商采购策略,对供应商的产能恢复决策进行分析,为存在供应断裂与产能恢复因素的供应链采购决策提供管理与实践上的参考。
3 问题描述与假设
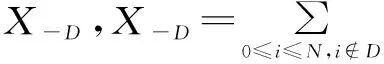
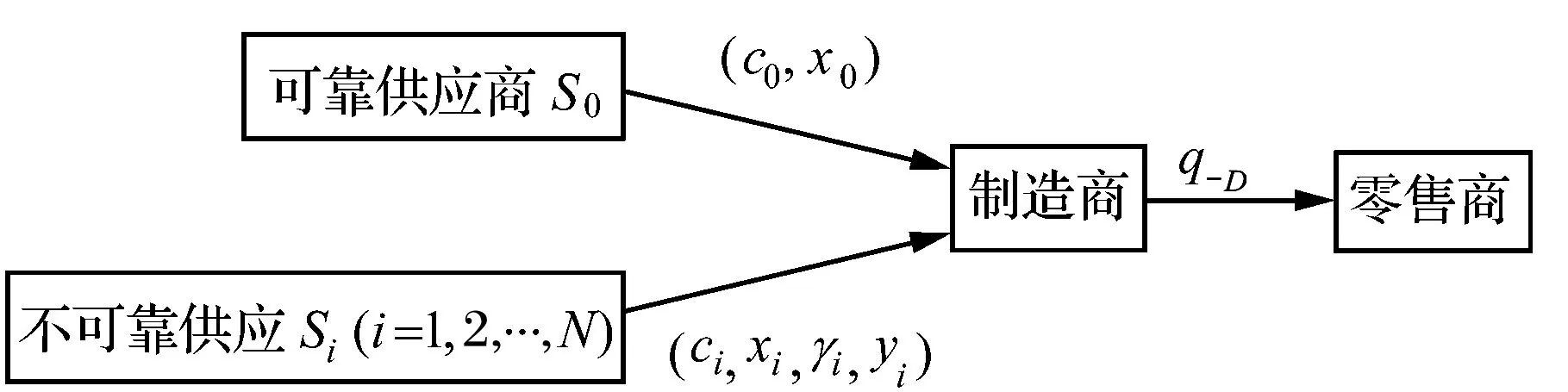
图1 多供应商-单制造商系统结构
制造商作为供应链系统中的核心企业,通过多源采购战略来激励供应商提升可靠性,降低供应风险,实现自身利润的最大化。用P(D)表示供应商{Si,i∈D}的供应断裂组合情况的概率。根据上述假设,制造商的利润函数为
(1)

(2)
根据集合D的取值范围,可知式(1)中包含了2N种可能性。其中,q-D表示某种供应断裂情况组合下的总销量,a-q-D/2为市场清算价格,因此,式(1)中第1个求和项表示制造商在面临供应断裂情况下的期望收益,第2项表示没有发生供应断裂情况下应支付的采购成本,第3项表示由于供应断裂和产能恢复而少支付的期望采购成本。约束分别表示每个供应商的订货量为非负,且制造商的销量应该小于原材料的采购量。然而,在现实中,每个供应商发生供应断裂而导致完全无法供货的概率很低,而一些经济和运营状况不佳的供应商发生供应断裂的概率相对较高,但是,制造商通常会通过供应商预选来规避该类供应商。另外,制造商通常也会采用分散策略(如地域上的分散)来选择供应商,因此,多家供应商同时发生供应断裂的概率会更低。当考虑多家供应商同时断裂时,模型共有2N+1个决策变量,解析解的求解也变得不可能。由此,本研究忽略多家供应商同时发生供应断裂的情况,将式(1)中的P(D)用γi近似表示,即仅考虑不可靠供应商单独发生供应断裂的情况,此时制造商的利润函数为
(3)
(4)
相关参数见表1。

表1 参数定义
4 制造商的最优订货决策分析
订货根据上述假设,在最优情况下,制造商同时向可靠和不可靠供应商订货,用U={i|1≤i≤u,xi>0}表示制造商所选择的不可靠供应商。
引理1 假设在最优情况下,制造商同时向可靠和不可靠供应商订货,那么,制造商将把最终收到的采购量全部制造成产品,即q-i=X-i+xiyi,i=0,1,…,N。
引理1排除了生产决策问题,有效简化了分析内容。这里它只作为一个技术简化手段,并不作为一个重要结论。根据引理1,在式(3)和式(4)中,用X-i+xiyi替换q-i,可得
(5)
(6)
定理1 在最优情况下,制造商向可靠和不可靠供应商订货,最优订货量如下
(7)
(8)
(9)
(10)
此时,
(11)
证明 根据引理1,定义约束xi≥0的拉格朗日乘数λi,制造商的利润最大化问题可转化为
(12)
(13)
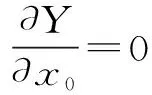
(14)
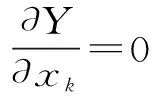
(15)
根据式(14)和式(15)可得
(16)

(17)
再由c0-ck(1-γk+γkyk)=γk(a-X-k-xkyk)(1-yk) =γk[a-X-0+xk(1-yk)](1-yk),可得
(18)
同理,可得
(19)
(20)
在讨论最优订货数量的性质之前,先讨论制造商同时向可靠和不可靠供应商订货的前提条件。制造商的边际效用函数r(q)=[(a-q/2)q]′=a-q≥0,所以总产量q不能超过a,即采购量不能超过a,否则制造商将不会把最终收到的采购量全部制造成产品。实际情况要求被选中的不可靠供应商、可靠供应商订货量大于0,所以u、a分别满足条件:
(21)
(22)
(23)
这些限定都属于决策成立的必要条件,用以进一步解释最优采购策略。
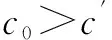
定理2将供应商断裂风险与产能恢复比率等因素考虑进成本核算,使得制造商能更准确地对可靠供应商的质量和数量进行选择。条件①保证了制造商向不可靠供应商订货,说明实现供应可靠性需要更多的成本投入,且从长期来看,当供应商在可靠性和成本两方面都具有优势时会更具竞争力。条件②由X-0≤a推导得出,它保证了制造商能够向可靠供应商订货,说明供应商对可靠性的投入也应控制在一定范围之内。在制定战略时,制造商倾向于刺激供应商之间竞争、培养亲密的供需关系,以降低供应商审核与管理成本,压低采购价格。条件③表明,在一个足够大的市场中,制造商更愿意向可靠供应商订货。

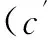
成本优势与供应风险比率的构成基于3点:①本研究探讨的供应风险用供应断裂风险表示;②本研究引入了可靠与不可靠供应商的概念,成本优势是基于可靠供应商的采购成本进行计算;③为简化分析,本研究仅考虑了一个不可靠供应商发生断裂的情况,而这种近似处理在大部分实际排序中仍然准确。
推论2 当制造商同时向可靠和不可靠供应商订货,并且被挑选的不可靠供应商U保持不变时,市场规模a增大,则制造商的总订货量X-0与可靠供应商订货量x0增大,不可靠供应商订货量xi不随市场规模a的变化而变化,i=1,2,…,N。
根据定理1中的决策公式,可以分析出推论2中的性质。当市场变大时,直觉认为制造商应该向所有供应商增加订货,然而推论2显示,只有可靠供应商订货量会随市场变大而变大,不可靠供应商订货量不会发生改变。推论2同定理2中的条件③很相似,即一个足够大的市场会使制造商更加倾向于可靠供应商。这里可以用边际效用函数r(q)=[(a-q/2)q]′=a-q予以解释,即当a处于不同水平时,边际效益发生改变,产量q的临界值改变,制造商的总订货量X-0与可靠供应商订货量x0随之发生变化,而不可靠供应商订货量xi(i=1,2,…,N)不变。
在全球供应链环境下,当制造商选择一家具有成本优势的海外供应商时,由于运输距离较远且存在一系列的干扰因素,海外供应商在影响速度和可靠性方面可能不如本地供应商。传统认知是企业必须在节约成本和响应度之间做出折中选择,但是推论2显示,从管理供应风险的角度而言,制造商可以同时实现节约成本和保持响应度的目标:制造商可以在早期向海外供应商采购,在获得更多市场信息以后,再向国内供应商采购,而不用在成本与响应度之间折中。
推论3 当其他条件保持不变,被选择的供应商改进自己的产能恢复比率yi时,则自身的订货量xi变大,但制造商的总订货量X-0、可靠供应商订货量x0和其他未投资产能恢复的不可靠供应商订货量xk(k∈uk=i)均减小。
当yi增大时,不可靠供应商的可靠性增加,制造商不必再订购多余的原材料来规避风险,从而制造商的总订货量减小;又因为不可靠供应商的单位成本不变,其竞争优势得以体现,使得制造商会将部分可靠供应商订货量转移给投资过产能恢复的不可靠供应商,即不可靠供应商的订货量xi会变大,而可靠供应商订货量x0会减小;并且,若其他不可靠供应商不投资产能恢复,则投资过产能恢复的不可靠供应商也会抢夺这些供应商的订单,即未投资产能恢复的不可靠供应商订货量xk(k∈uk=i)也减小。
供应商无法完全消除断裂风险,但是,通过投资产能恢复可以降低供应断裂风险带来的损失。产能恢复比率增加时,向不可靠供应商采购的量也会增加,制造商对可靠供应商的依赖性就会降低,使得供应风险更加分散,采购活动更加安全。在多源采购情境中,制造商不仅需要对供应商进行充分分级评估,更要适时予以激励。供应链中激励的作用广泛运用于各行各业,提高产能恢复能力对买方企业(制造商)而言是一个十分有效的战略。与向可靠但昂贵的供应商采购相比,制造商对价格激励和数量激励的适当运用常常能化解一部分采购风险,降低采购成本,给企业带来更高的收益。
5 供应商的产能恢复投资决策分析
当供应商没有投资产能恢复时,即yi=0,若发生供应断裂,供应商将不会获得任何收益;当供应商有投资产能恢复时,即yi>0,若发生供应断裂,如果该供应商被选择,那么将能够获得产能恢复收益。
供应商投资产能恢复存在两个方面的成本:①对于不同的产能恢复比率yi,供应商的变动成本为Cs=ki(yi)2/2,ki>0,与之类似的成本函数广泛应用于生产运作与市场营销研究领域中[26];②对于厂房、机器等固定资产的投资成本为Fi。供应商Si的单位成本为ωi,由于单位成本一般小于单位批发价格,因此,假设ωi (24) (25) 同时,考虑供应断裂与产能恢复因素,供应商的利润不仅受供应断裂风险和产能恢复比率、订货量的影响,也受制造商的采购价格和固定投资成本的影响。 推论4 当供应商的投资成本系数ki较小时,制定的产能恢复比率更高,此时,供应商应尽可能地提高恢复比率,以获得最大利润,最大利润为(1-γi)(ci-ωi)xi+[(ci-ωi)xiyi-ki(yi)2/2]γi-Fi,0≤yi≤1。 推论4说明,供应商在做决策时,应充分掌握产能恢复投资成本的信息,当供应商的投资成本系数较小时,供应商的最优决策就是尽可能地提高产能恢复比率,以获得最大利润值。 推论5 当制造商的订货量xi增大时,供应商制定的最优产能恢复比率yi也会增大,两者相互影响,当调整到下列等式成立时,yi值到达平衡点: (26) 推论5说明,若供应商在做决策时提高产能恢复比率,那么制造商也会增加订货量,进一步刺激供应商提高可靠性。供应商投资产能恢复不仅增加了自身利润,同时巩固了同制造商之间的合作关系,有利于降低供应风险,达到双赢局面。制造商的订货量决策与供应商的产能恢复比率决策是一个相互影响、相互促进的过程,直到双方就同一产能恢复比率所制定的决策相匹配,即双方的决策达到一个均衡点,不再继续变化。在实际操作过程中,双方决策过程还会受到其他因素的影响,如资金成本、人力成本、市场大小变动等。由此,只有当市场保持平稳,双方的成本保持不变的情况下,才能到达均衡状态。 通过投资产能恢复,供应商不仅能够降低供应风险可能带来的损失,还能在同其他供应商的竞争中,增加自己的竞争优势。供应商经过分析计算,能够找到一个最优的产能恢复比率,使得自身利润最大。此类事前投资战略可以有效降低供应风险,强化供应链上下游企业间的合作,使得供应商在多源竞争环境中保持优势地位。 本研究针对一个多供应商-单制造商的供应链网络模型,考虑供应断裂与产能恢复因素,以制造商利润最大化为目标,建立了一个采购联合优化模型来研究制造商的采购策略,同时,对供应商的产能恢复决策进行分析。研究表明:不可靠供应商的最优订单按照成本优势与供应风险比率排序,且与市场大小无关; 当被选择的不可靠供应商改进自己的产能恢复比率时,自身的订货量变大,但制造商的总订货量、可靠供应商的订货量和其他未投资产能恢复的不可靠供应商的订货量均减小;供应商的产能恢复投资决策表明,只有当供应商的固定投资成本足够小或者制造商的采购价格足够大时,供应商才会投资产能恢复;当供应商的投资成本系数较小时,供应商会尽量提升自己的产能恢复比率来最大化自己的利润;反之,存在一个最优的产能恢复比率。 本研究从定量角度为存在供应断裂与产能恢复因素的供应链采购决策提供了管理与实践上的参考,即通过多源采购与激励策略来降低供应断裂风险带来的损失,但如何设计激励合约来鼓励产能恢复并降低供应链的损失,是一个非常有意义的研究问题。另外,生产质量风险与供应断裂风险在实践中同时存在,讨论一种包含多种形式的供应风险的模型,也是未来拓展供应风险管理领域的一个重要研究方向。 [1] 孙承志,罗侠.供应链中供应不确定性的影响因素及对策研究[J]. 经济研究导刊, 2013(11): 146~147 [2] BERLKIN D, MACHALABA D. Canada Rail Strike Disrupts Supply Chain[EB/OL]. (2007-02-22)[2016-05-02].http://www.wsj.com/articles/SB117209999343215413 [3] JOHNSON T. Oil’s Trouble Spots[EB/OL]. (2012-01-20)[2016-05-02].http://www.cfr.org/middle-east-and-north-africa/oils-trouble-spots/p17068 [4] ZSIDISIN G A. A Grounded Definition of Supply Risk [J]. Journal of Purchasing and Supply Management, 2003, 9(5/6): 217~224 [5] TOMLIN B, WANG Y. Operational Strategies for Managing Supply Chain Disruption Risk [M]// KOUVELIS P, DONG L, BOYABATLI O, et al. Handbook of Integrated Risk Management in Global Supply Chains. Hoboken: John Wiley & Sons,2012:79~101 [6] HEYES W. Honest Broker Solves Supply Problems [EB/OL]. (2008-03-26)[2016-03-01]. http:// www.dpaonthenet.net/articla.aspx?ArticleID=14675 [7] HU B, KOSTAMIS D. Managing Supply Disruptions When Sourcing from Reliable and Unreliable Suppliers[J]. Production and Operations Management, 2015, 24 (5): 808~820 [8] HU X, GURNANI H, WANG L. Managing Risk of Supply Disruptions: Incentives for Capacity Restoration [J]. Production and Operations Management, 2013, 22(1): 137~150 [9] MEYER R R, ROTHKOPF M H, SMITH S A. Reliability and Inventory in a Production-Storage System[J]. Management Science, 1979,25(8): 799~807 [10] BIELECKI T, KUMAR P R. Optimality of Zero-Inventory Policies for Unreliable Manufacturing Systems [J]. Operations Research, 1988, 36(4): 532~541 [11] GURNANI H, AKELLA R, LEHOCZKY J. Supply Management in Assembly Systems with Random Yield and Random Demand [J]. IIE Transactions, 2000, 32(8): 701~714 [12] DADA M, PETRUZZI N C, SCHWARZ L B. A Newsvendor Model with Unreliable Suppliers[EB/OL].(2003-08-03)[2016-02-05]. http://business.illinois.edu/working_papers/papers/03-0112.pdf [13] TOMLIN B, WANG Y. On the Value of Mix Flexibility and Dual Sourcing in Unreliable Newsvendor Networks [J]. Manufacturing & Service Operations Management, 2005, 7(1): 37~57 [14] TANG C S. Perspectives in Supply Chain Risk Management [J]. International Journal of Production Economics, 2006, 103(2): 451~488 [15] HE B, HUANG H, YUAN K. Managing Supply Disruption through Procurement Strategy and Price Competition [J]. International Journal of Production Research, 2016, 54(7): 1 980~1 999 [16] XU X, SHANG J, WANG H, et al. Optimal Production and Inventory Decisions under Demand and Production Disruptions [J]. International Journal of Production Research, 2016, 54(1): 287~301 [17] GIRI B C, BARDHAN S. Coordinating a Supply Chain under Uncertain Demand and Random Yield in Presence of Supply Disruption [J]. International Journal of Production Research, 2015, 53(16): 5 070~5 084 [18] GUPTA V, HE B, SETHI S P. Contingent Sourcing under Supply Disruption and Competition [J]. International Journal of Production Research, 2015, 53(10): 3 006~3 027 [19] 肖勇波, 陈剑, 吴鹏. 产能和需求不确定情形下ATO系统最优库存和生产决策研究 [J]. 中国管理科学, 2007, 15(5): 56~64 [20] 温源, 肖勇波. 面临汇率和供应风险的双渠道采购决策研究 [J]. 中国管理科学, 2013, 21(4): 35~43 [21] 马士华, 李果. 供应商产出随机下基于风险共享的供应链协同模型 [J]. 计算机集成制造系统, 2010, 16(3): 563~572 [22] 何青,黄河.可改善供应风险和生产成本下的供应渠道策略研究[J]. 管理学报,2016,13(5):755~762 [23] 徐和,彭伟真.供应风险下产品价格和质量水平的均衡策略研究[J]. 管理学报,2016,13(7):1 090~1 094,1 104 [24] 朱传波, 陈畴鏞, 包兴. 供应中断风险下供应链恢复能力投资决策及协调 [J]. 工业工程, 2014, 17(3): 27~32 [25] DONG L, TOMLIN B. Managing Disruption Risk: The Interplay between Operations and Insurance [J]. Management Science, 2012, 58(10): 1 898~1 915 [26] DADA M, PETRUZZI N C, SCHWARZ L B. A Newsvendor’s Procurement Problem When Suppliers Are Unreliable [J]. Manufacturing & Service Operations Management, 2007, 9(1): 9~32 (编辑 桂林) Managing Supply Disruption and Capacity Restoration When a Manufacture Sourcing from a Reliable and Multiple Unreliable Suppliers DAI Bin FAN Lei TIAN Ying (Wuhan University, Wuhan, China) This study examines a supply chain consisting of multiple suppliers and one manufacture, considering both supply disruption and capacity restoration factors in maximizing the manufacture’s profit, to investigate the procurement strategy of the manufacture and the capacity restoration strategy of suppliers. It is found that the optimal orders of the unreliable suppliers are ranked by the ratio of cost advantage and supply risk, and are not subject to market size changes. The capacity restoration strategy of suppliers shows that only when the fixed investment cost is sufficiently small or the purchase price is sufficiently large, the supplier needs to invest capacity restoration. When the investment cost coefficient of the supplier is small enough, the supplier will promote its capacity restoration proportion extensively to maximize its own profit. While when the investment cost coefficient of supplier is large enough, there exists an optimal capacity restoration proportion. supply disruption; capacity restoration; multiple-sourcing; procurement strategy 10.3969/j.issn.1672-884x.2016.12.011 2016-05-13 国家自然科学基金资助项目(71301122,71671133);湖北省技术创新专项软科学研究类资助项目(CXRK2016000001) C93 A 1672-884X(2016)12-1826-08 戴宾(1983~),男,湖南邵阳人,武汉大学(武汉市 430072)经济与管理学院副教授,博士。研究方向为物流与供应链管理。E-mail: bin_dai@whu.edu.cn
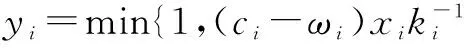
6 结语

