水库防洪错峰调度风险分析方法及应用
刘克琳, 王宗志, 程亮, 胡四一
(南京水利科学研究院 水文水资源与水利工程科学国家重点实验室,江苏 南京 210029)
水库防洪错峰调度风险分析方法及应用
刘克琳, 王宗志, 程亮, 胡四一
(南京水利科学研究院 水文水资源与水利工程科学国家重点实验室,江苏 南京 210029)
水库防洪错峰调度是一种利用下游区间洪水预报信息的防洪预报调度方式,能有效减小水库防洪库容,提高洪水资源利用率,但受区间洪水预报、水库下泄洪水传播时间、调度滞时等不确定因素的影响,水库下游防洪风险的可能性将增加。综合考虑多个不确定因子,采用蒙特卡洛法、风险标准法等,提出了基于错峰调度规则的拟定、风险的定义、风险因子的识别与量化、风险率计算、方案决策过程的水库防洪错峰调度风险分析的流程与方法,并将上述方法应用于海河流域的密云水库。研究结果表明:通过采用提出的防洪错峰调度方案,密云水库能抬高汛限水位2.0 m,减小防洪库容3.09亿m3;而承担的水库防洪错峰调度风险率仅为11%;延长错峰时间能显著降低防洪错峰调度的风险。
水库防洪错峰调度;不确定性因子;风险分析;蒙特卡洛法
依托天气预报和洪水预报技术的进步,挖掘水库防洪预报调度的潜力、实现水库在汛期安全有效的蓄水,是洪水资源利用的重要途径[1]。水库防洪错峰调度是水库防洪预报调度的主要方式之一,它依据水库下游的区间洪水预报信息,在区间洪峰来临前及时减小水库泄量,使水库泄量与区间洪水的组合流量不超过下游防洪控制断面的安全泄量[2]。与不考虑预报信息的固定泄流方式相比,水库防洪错峰调度方式可在保证下游防洪安全的前提下加大泄量,从而有效减小预留的防洪库容,增加水库兴利效益,但受区间洪水预报、水库下泄洪水传播时间、调度滞时等不确定因素的影响,可能会增加水库下游的防洪风险[3-4]。因此,识别及量化水库防洪错峰调度运行中的不确定性因子和评估防洪错峰调度的风险,对洪水资源利用率的提高具有重要意义。
在水库防洪预报调度的风险分析方面,2004年,姜树海等[5]通过引入水库调洪演算随机数学模型,论证了洪水预报精度对水库防洪预报调度风险率的影响;2005年,侯召成等[6]评估了水库不同起调水位与不同预报误差组合下的水库防洪风险度;2010年,刁艳芳等[7]综合考虑了洪水预报误差、水库库容、泄流能力以及调度滞时的不确定性,采用蒙特卡洛法计算了水库及下游的防洪风险。以往的研究成果多针对以入库洪水预报为预报信息的水库防洪预报调度方式,鲜见对以水库下游区间洪水预报为预报信息的防洪错峰调度进行风险分析的成果。为此,本文拟从制定水库防洪错峰调度规则出发,按照风险的定义、不确定性因子的识别与量化、风险率计算、方案决策等流程提出水库防洪错峰调度风险分析方法,并应用于海河流域的密云水库。
1 水库防洪错峰调度规则的拟定
以防洪标准频率的区间设计洪水过程作为依据,制定水库防洪错峰调度规则。需要确定错峰起止时间及判断指标、错峰流量和其他时段水库泄量。根据水库防洪错峰调度的原理(图1),水库泄量在防洪控制断面上的响应过程q(t)应满足:
(1)
式中:Qc为错峰流量;Q1为其他时段水库泄量;Qa为防洪控制断面的安全流量;Qpm为区间防洪标准设计洪峰流量;Q(t)为区间防洪标准设计洪水过程;Qy为区间预报流量阈值,被作为判断错峰起止时间的指标。

图1 水库防洪错峰调度示意图
其他时段水库泄量Q1除满足式(1)外,还应满足:
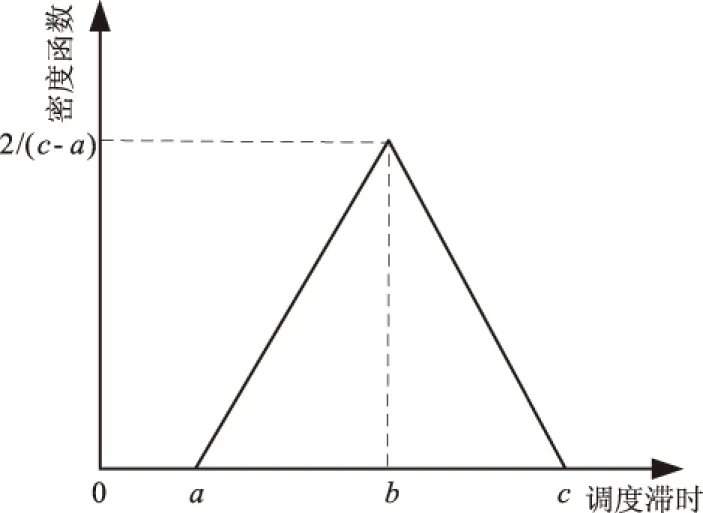
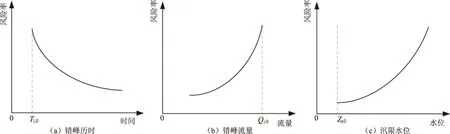
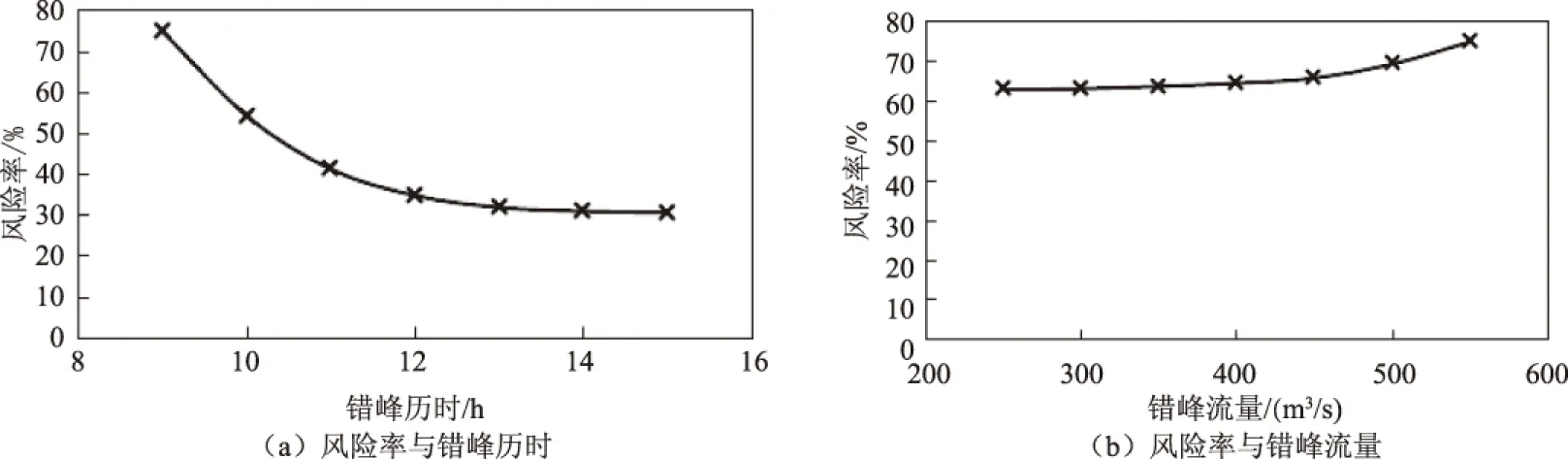
Qc (2) 式中Q2为上一级水库控泄流量,当不存在上一级保护对象时为水库泄流能力。 设水库泄量传播至防洪控制断面的时间为tc,由水库调度决策、指令传递、泄洪闸门启闭时间等产生的调度滞时为tz,区间预报流量阈值Qy在涨水段和退水段对应的时间分别为t1和t2,则水库错峰开始时间ta和结束时间tb应满足: 0≤ta≤t1-tc-tz; (3) tb≥t2-tc-tz。 (4) 水库错峰历时TL为: TL=tb-ta。 (5) 由式(3)可知,区间洪水预报的有效预见期应不小于水库泄流传播时间与调度滞时之和。这也是水库能采用防洪错峰调度方式的基本条件。 2.1 风险的识别与定义 水库防洪调度的风险主要包括库区淹没风险、水库大坝风险和水库下游防洪风险。其中,库区淹没风险和水库大坝风险主要与水库调洪高水位有关,而下游防洪风险主要受水库泄量和区间洪水的影响。水库防洪错峰调度的调度目标为下泄水量与区间洪水的组合流量不超过防洪控制断面的安全泄量;其主要风险是由于错峰不成功而导致的水库下游防洪风险。因此,水库防洪错峰调度的风险可定义为:由于水库泄量与区间洪水错峰不成功而导致的防洪控制断面流量超过安全泄量的概率及损失。本文主要研究风险发生的概率,即水库防洪错峰调度风险率Pf, Pf=P(Qzm≥Qa)。 (6) 式中Qzm为水库泄量与区间洪水的组合洪峰流量。 2.2 不确定性因子的识别与量化 影响水库防洪错峰调度风险的不确定性因子主要包括区间洪水预报、洪水传播时间及调度滞时,其本身具有的随机性是导致错峰不成功事件发生的风险源。通过定义随机变量、拟合分布函数等过程,对不确定性因子进行量化,是水库防洪错峰调度风险率计算的前提和基础。 2.2.1 区间洪水预报的不确定性 区间洪水预报的不确定性应考虑洪峰流量Qpm和峰现时间tm。在已发布预报值的前提下,其实际可能值应满足正态分布[8]: (7) 式中:EQpm、Etm分别为洪峰流量和峰现时间实际可能的期望值,期望值大小与预报值相一致;σQpm、σtm为均方差,根据洪水预报的误差评定结果给定。 2.2.2 洪水传播时间的不确定性 受水库下游河道断面的水力参数、糙率等不确定性因素的影响,洪水传播时间具有一定的不确定性。可采用正态分布对洪水传播时间进行描述: (8) 式中:Etc、σtc分别为洪水传播时间的期望值和均方差,可根据水库泄量和防洪控制断面流量的观测资料统计得到。 2.2.3 调度滞时的不确定性 调度滞时的不确定性来源于调度决策、指令传递、泄洪闸门启闭时间的不确定性,可采用结构比较简单的三角分布密度函数进行描述,其密度函数[7]可表示为: (9) 式中a、b、c分别为调度滞时的最小值、最可能值和最大值。 调度滞时三角分布密度函数曲线如图2所示。 图2 调度滞时三角分布密度函数曲线 2.3 风险率的计算 根据错峰调度的基本原理和存在的不确定性因子,发生的错峰风险事件主要包括两种情景:①错峰时间上出现偏差,使得区间洪峰与水库其他时段流量(一般大于错峰流量)相遇;②虽然在错峰时间上无偏差,但实际出现的区间洪峰流量比预报值偏大,导致组合流量超过了安全泄量。 根据水库防洪错峰调度风险的定义和式(6),可得极限状态方程为: max(q(t)+Q(t))-Qa=0。 (10) 式中:q(t)受调度滞时、洪水传播时间不确定性的影响;Q(t)受区间洪水预报不确定性的影响。但由于不确定性因子在极限状态方程中不能显式表达,无法选择直接积分法、一次二阶矩法等方法计算风险率,而蒙特卡洛法是一种求解类似问题行之有效的方法。 2.3.1 生成随机数 影响水库防洪错峰调度风险的不确定性因子包括Qpm、tm、tz、tc,其中Qpm、tm、tc为正态分布,可采用变换法生成随机数。tz为三角分布,可采用分布函数抽样的方法,考虑等式: (11) 式中ε为在[0,1]区间上均匀分布的随机数。根据式(9)和式(11),可得到服从三角分布的tz随机数。 由于不确定性因子Qpm、tm、tz、tc在物理成因上 不存在相关性(Qpm和tm可能存在弱相关性,本文限于篇幅不再探讨),因此,可采用独立抽样的方法生成一组随机数。在随机数生成之后,需要对其进行假设性检验,当不通过检验时需要重新生成。 2.3.2 计算风险率 按照以上方法生成n组Qpm、tm、tz、tc随机数。根据Qpm和tm随机数模拟实际发生的区间洪峰流量及出现时间;根据tz、tc随机数以及调度规则拟定的错峰时间、错峰流量等指标模拟实际下泄流量过程。将区间洪峰流量与水库下泄流量进行组合,统计其组合过程的最大值Qzm,比较判断Qzm是否超过Qa,超过的次数记为m,则水库防洪错峰调度风险率可表示为: (12) 当随着模拟次数n的增加,Pf值稳定于某一值时,即可停止模拟,并将该稳定值作为水库防洪错峰调度风险率计算的最终值。 由水库防洪错峰调度规则拟定的初始方案可知,该方案没有为不确定性因子提供安全余量,一般而言会具有较大风险。通过调整错峰调度方案的指标值,建立指标值与风险率的相关关系,再依据一定的风险标准决策出一组合理的方案指标值,是水库防洪错峰调度方案决策的主要目的。 在不确定性因子随机特征无法改变的前提下,通过延长错峰历时、减小错峰流量能降低不确定性因子带来的影响,从而减小错峰调度的风险,但会占用水库较多的防洪库容,相比固定泄流方式抬高的汛限水位也相应降低。错峰历时TL、错峰流量Qc、汛限水位Zx与错峰调度风险率Pf的关系如图3所示。图中,TL0、Qc0、Zx0分别为初始方案的错峰历时、错峰流量以及固定泄流调度方案的汛限水位。 图3 错峰历时TL、错峰流量Qc、汛限水位Zx与错峰调度风险率Pf的关系图 为了保证错峰调度方案达到可投入使用的程度,方案本身应满足一定的可靠性。本文定义的错峰调度风险可理解为从风险率的角度评价错峰调度方案的可靠性,其风险率与可靠度之和应等于1。错峰调度可能导致下游发生标准内洪水时河道行洪流量超过安全泄量,严重时可导致发生洪水漫堤或溃堤事故,给下游保护区带来不必要的淹没损失。在一般情况下,河道本身的蓄洪能力较小,当发生错峰调度风险时,除了应急加高河道堤防以外,可供选择的弥补措施较少。因此,错峰调度风险应控制在较低的水平。参照水库防洪预报调度对洪水预报方案的要求,甲级洪水预报方案能达到可利用的水平,其可靠度(合格率)不低于85%。因此,建议水库防洪错峰调度风险率不超过15%。 密云水库位于海河流域潮白河上游,为保证下游苏庄站的行洪安全,水库防洪标准设为50年一遇。当发生50年一遇设计洪水时,密云水库控泄流量为600 m3/s(包括京密引水渠引水50 m3/s,河道下泄流量550 m3/s)[9-10]。由于密云水库50年一遇的控泄流量偏小,水库预留的防洪库容偏大,从而限制了密云水库兴利效益的发挥,因此有必要研究密云水库与下游苏密怀区间洪水的错峰调度方案。 4.1 初始方案拟定 密云水库下游苏庄站的安全流量为3 000 m3/s,扣除怀柔水库下泄流量400 m3/s,实际安全流量Qa为2 600 m3/s;苏密怀区间50年一遇设计洪峰流量Qpm为2 050 m3/s。根据式(1),计算错峰流量Qc=Qa-Qpm=550 m3/s。取区间预报流量阈值Qy为1 400 m3/s,计算其他时段水库泄量Q1=Qa-Qy=1 200 m3/s。 苏密怀区间的洪水预报有效预见期为14 h,密云水库泄流传播至防洪控制断面的历时tc为10 h,调度滞时tz为1 h,根据苏密怀区间的设计洪水过程得t1为14.5 h,tm为18 h,t2为22.5 h。根据式(3),计算水库错峰开始时间ta≤t1-tc-tz=3.5 h,为安全计,取3 h。根据式(4),计算水库错峰结束时间tb≥t2-tc-tz=11.5 h,取12 h。根据式(5),计算错峰历时TL=tb-ta=9 h。 根据以上结果,提出密云水库防洪错峰调度初始方案的指标值,详见表1。 表1 密云水库防洪错峰调度初始方案指标值 4.2 风险因子量化 根据统计资料,估计洪峰流量Qpm、峰现时间tm、洪水传播时间tc、调度滞时tz的特征值,具体见表2。 表2 密云水库防洪错峰调度主要风险因子特征值 4.3 风险计算与决策 根据洪峰流量、峰现时间、洪水传播时间、调度滞时4个随机变量的特征值,模拟生成10万组随机序列,结合密云水库防洪错峰调度初始方案(表1),利用式(12)计算错峰调度风险率。计算结果表明,密云水库防洪错峰初始调度的风险较大,风险率可达75%。 以初始方案为基础,分别测算延长错峰历时和减小错峰流量两种措施,其对降低防洪错峰调度风险率的效果,如图4所示。由图4可知,在保持其他指标不变的前提下,延长错峰历时的措施对降低密云水库防洪错峰风险率的效果明显大于减小错峰流量的效果。 图4 密云水库防洪错峰调度风险率与错峰历时、错峰流量的关系 按照密云水库防洪错峰调度风险率对错峰历时和错峰流量的敏感性,拟定错峰历时和错峰流量的组合方案,并计算各方案的防洪错峰调度风险率,结果见表3。 表3 密云水库错峰历时和错峰流量组合方案的风险率计算结果 由表3可知,同时增加错峰历时和减小错峰流量能更有效地降低错峰调度风险率。当错峰历时为13 h,错峰流量为470 m3/s时,风险率仅为11%,满足不超过15%的风险标准,可将其作为密云水库防洪错峰调度的推荐方案。根据错峰调度规则进行调洪演算,推求出密云水库汛限水位为152.0 m,相比固定泄流方案的汛限水位抬高了2.0 m,可减小防洪库容3.09亿m3。 密云水库防洪错峰调度方案具体描述为:当水库水位超过汛限水位152.0 m时,水库控泄流量1 200 m3/s;当预报区间洪水处于涨水段且流量达到1 400 m3/s时,水库在1 h后开始错峰并控泄流量470 m3/s,错峰13 h或预报区间洪水退水流量低于1 400 m3/s时,水库恢复控泄流量1 200 m3/s。 水库防洪错峰调度方式利用了水库下游区间的洪水预报信息,能有效地减小水库防洪库容,增加水库兴利效益。但受到区间洪水预报、水库下泄洪水传播时间、调度滞时等不确定性因素的影响,有可能会增加水库下游的防洪风险。因此,识别防洪错峰调度过程中可能存在的风险因子,定量估计防洪错峰调度带来的风险,是水库防洪错峰调度方案能否应用于实际调度的关键。本文综合考虑了洪水预报的洪峰流量、峰现时间、洪水传播时间、调度滞时共4个风险因子,提出了水库防洪错峰调度的风险分析方法,并应用于海河流域密云水库。主要结论有: 1)区间洪水预报的有效预见期应不小于水库泄流传播时间与调度滞时之和,这是水库采用防洪错峰调度方式的基本条件。 2)水库防洪错峰调度的风险主要是水库下游防洪风险,可定义为由于水库泄水与区间洪水错峰不成功而导致的防洪控制断面流量超过安全泄量的概率及损失。 3)将提出的水库防洪错峰调度风险分析方法应用于海河流域的密云水库,可知密云水库通过采用防洪错峰调度方案,能抬高汛限水位2.0 m,减小防洪库容3.09亿m3,而承担的水库防洪错峰调度风险率仅为11%。 4)在不确定性因子随机特征无法改变的条件下,通过延长错峰时间、减小错峰流量能降低不确定性因子带来的影响,从而减小错峰调度的风险,但同时会占用水库更多的防洪库容,相比固定泄流方式抬高的汛限水位也相应降低。密云水库的实例运用表明,延长错峰时间对降低风险的效果最为显著。 5)本文在水库防洪错峰调度的方案制定、风险分析等方面主要依据设计洪水过程和调度规则,因此更偏于规划层面,在风险计算时未考虑区间洪水过程的不确定性。今后应重点结合实时调度,分析水库防洪错峰调度过程中的动态风险。 [1]胡四一,高波,王忠静.海河流域洪水资源安全利用:水库汛限水位的确定与运用[J].中国水利,2002(10):105-108. [2]吴如发.隔河岩水库与长江洪水错峰调度研究[J].人民长江,2001,32(1):39-43. [3]闫宝伟,郭生练.考虑洪水过程预报误差的水库防洪调度风险分析[J].水利学报,2012,43(7):803-807. [4]吴成国,王义民,金菊良,等.基于三角模糊数的水库防洪调度模糊综合风险分析[J].水力发电学报,2011,30(4):30-35. [5]姜树海,范子武.水库防洪预报调度的风险分析[J].水利学报,2004,35(11):102-107. [6]侯召成,翟宜峰,殷峻暹.水库防洪预报调度风险分析研究[J].中国水利水电科学研究院学报,2005,3(1):16-21. [7]刁艳芳,王本德.基于不同风险源组合的水库防洪预报调度方式风险分析[J].中国科学:技术科学,2010,40(10):1140-1147. [8]李整,陈代海,曹宁宁.三角形综合单位线法洪峰预报研究[J].华北水利水电大学学报(自然科学版),2016,37(4):78-82. [9]廖松.改进密云水库汛期调度方案的途径[J].水文,1996,16(1):10-15. [10]卢丽,徐千军,保其长,等.密云水库错峰调度的可行性分析[J].水力发电学报,2008,27(2):1-5. (责任编辑:张陵) Risk Analysis Method and Application of Reservoir Flood Peak Staggered Regulation LIU Kelin, WANG Zongzhi, CHENG Liang, HU Siyi (State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, Nanjing Hydraulic Research Institute, Nanjing 210029, China) Flood peak staggered regulation (FPSR) is a flood forecasting and dispatching method which utilizes downstream flood forecast information. It can effectively reduce the reservoir capacity of flood control, and improve flood resource utilization. However, there is the possibility of increasing flood risk in the lower reaches of the reservoir due to the influence of uncertainties such as interval flood forecasting, flood discharge time of reservoir discharge, and scheduling delay. In this paper, considering multiple uncertain factors, using the Monte Carlo method and the risk standard method, a FPSR risk analysis method is proposed consisting of FPSR rule formulation, risk definition, risk factor identification and quantification, risk rate calculation, scheme decision and so on. The method is applied to Miyun Reservoir of Haihe River Basin. The results show that: by adopting the proposed flood control peak-shifting scheduling scheme, Miyun Reservoir can raise the flood limit water level of 2.0 m, reduce the flood storage capacity of 309 million m3, while the risk rate is only 11%. Further research shows that prolonging the peak shifting time can significantly reduce the risk of erroneous scheduling. flood peak staggered regulation; uncertainty factors; risk analysis; Monte Carlo method 2016-09-06 国家自然科学基金项目(51409169,51279223);水利部公益性行业专项经费项目(201501054);国家重点研发计划课题(2016YFC0400906);山东省重大水利科研与技术推广项目(SDSLKY201316)。 刘克琳(1981—),男,山东济南人,高级工程师,硕士,主要从事水库调度及不确定性分析方面的研究。E-mail:klliu@nhri.cn。 王宗志(1977—),男,山东邹平人,教授级高级工程师,博士,主要从事水资源系统工程及防洪减灾方面的研究。E-mail:zzwang@nhri.cn。 10.3969/j.issn.1002-5634.2016.06.008 TV697.1+1 A 1002-5634(2016)06-0043-062 水库防洪错峰调度的风险计算
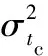
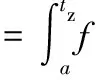
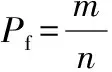
3 水库防洪错峰调度方案的决策
4 实例应用



5 结语

