基于渗流法的泡沫铝细观结构模型研究*
冯 阳, 梁增友, 吴鸿超, 陈智刚
(1. 中北大学 机电工程学院, 山西 太原 030051; 2. 地下目标毁伤技术重点学科实验室, 山西 太原 030051)
基于渗流法的泡沫铝细观结构模型研究*
冯阳1,2, 梁增友1,2, 吴鸿超1,2, 陈智刚1,2
(1. 中北大学 机电工程学院, 山西 太原 030051; 2. 地下目标毁伤技术重点学科实验室, 山西 太原 030051)
摘要:泡沫铝能在较低的流动应力下产生较大的塑性变形, 是一种优异的缓冲吸能材料. 渗流法是目前较成熟的工业化生产开孔泡沫铝的方法之一, 基于该方法的工艺流程, 采用蒙特卡罗法和重力堆积法建立了泡沫铝的细观结构模型. 结合SPH算法在应变率范围为10~10 000 s-1内对泡沫铝的压缩行为进行数值模拟, 并分析了泡沫铝的变形失效模式. 结果表明:基于渗流法的数值模拟方法可以反映泡沫铝的动态压缩过程, 并且高应变率下泡沫铝的变形模式与中低应变率相比存在明显的差异.
关键词:开孔泡沫铝; 细观结构; 渗流法; 数值模拟
泡沫铝是一种新型的结构和功能一体化材料. 由于金属基体内含有大量胞孔以及多样性的细观结构, 使其具有轻质、 高比强度、 高能量吸收等优异的力学性能和吸热、 隔热、 降噪、 电磁屏蔽等多功能复合的特性[1]. 正是由于泡沫铝兼具多种性能于一体, 其被广泛应用于车辆、 航空、 航天和军事等领域[1-3].
1983年, G.J.Dvies发表的论文是人类开始系统化研究泡沫金属的标志[4], 随后30多年, 学者不断致力于探索泡沫金属的细观结构. Gibson和Ashby以正立方体胞元为基础描述泡沫材料相关特征, 对于开孔泡沫材料使用12条棱杆, 而对于闭孔泡沫材料还要加入6个封闭胞壁[5]. 随后有学者建立了更加复杂的正十四面体模型, 也称Kelvin模型, 其包含6个正四边形和8个正六边形, 共计36条棱杆和24个顶点. Zhu等利用Kelvin模型研究了泡沫金属的弹性性能和动态力学行为[6-7]. Ahmed S. Suleiman通过一个立方体和若干球体之间的布尔运算得到了一种近似于正十四面体的单胞模型, 并对其进行周期排列, 研究了液体流过开孔泡沫铝时的流场和压力降[8].
但是泡沫铝中的胞孔排列具有随机性、 不均匀性等缺陷, 仅采用规则的胞元进行周期排列得到的几何模型不能准确地还原材料的特征. 为了在模型中体现胞孔形状的不规则性和空间排列的随机性, 许多学者利用Voronoi模型构建了开孔和闭孔泡沫铝几何模型, 并进行了尺寸效应、 泡沫杆撞击刚性墙和动态压缩力学性能等更加广泛的研究[9-11]. 近年来, X射线CT扫描技术逐渐被运用到泡沫材料细观结构的研究中, 其首先对试件进行横断面扫描, 然后利用图像处理技术重构几何模型, 与传统方法相比, 该项技术能够较准确地还原泡沫材料的内部特征, 获得较真实的数值模拟结果[12-13].
本文从开孔泡沫铝的生产工艺流程入手, 着重介绍了一种基于渗流法的泡沫铝细观结构数值模拟方法. 根据所提出的方法, 采用SPH算法, 通过自编的前处理程序生成几何模型, 利用LS-DYNA进行了10~10 000 s-1应变率范围内的压缩数值模拟, 分析了应变率对泡沫铝动态力学行为的影响以及泡沫铝的变形失效模式.
1泡沫铝细观结构模型
1.1渗流法的工艺流程
渗流法是目前较成熟的工业化生产开孔泡沫铝的方法之一. 其工艺流程如图 1 所示, 具体步骤为: ① 将可溶于水的颗粒(如NaCl、 KCl或MgSO4晶体颗粒)填充到模具中并混合均匀; ② 适当压缩制成坯体并进行预热; ③ 加压使铝液渗入到晶体颗粒组成的缝隙中; ④ 进行相关热处理, 冷却后用水将可溶性颗粒去除. 上述4个步骤对制得的泡沫铝参数及性能均有影响, 其中步骤①中颗粒的参数以及颗粒堆积体的形态影响泡沫铝的孔径、 孔隙率和通孔率等重要参数.
考虑到已经有学者成功制备出球形孔泡沫铝, 且球形孔低孔隙率泡沫铝合金的吸能能力较多边形孔高孔隙率泡沫铝合金高[14], 为了适当简化模型, 数值模拟中假设可溶性颗粒均为完美的球体.

图 1 渗流法生产开孔泡沫铝的主要工艺过程Fig.1 Main process to manufacture open-cell aluminum foam using infiltration casting methods
1.2泡沫铝几何模型的建立
为了建立较符合实际的细观结构几何模型, 从渗流法生产工艺入手, 将影响泡沫铝性能的主要生产参数在模型中得到体现. 由于泡沫铝的压缩过程是一个大位移、 大转动过程, 为了保证计算结果的收敛性, 采用SPH算法可以获得较好的精度和时间经济性. 与实际上先有球形晶体颗粒堆积体后有开孔泡沫铝的生产过程有所不同的是数值模拟中首先建立一个SPH粒子数为m×n×l的块体(类似于充满铝液的模具), 然后根据每个球体晶体颗粒的球心坐标和半径将包含在此球形空间中的SPH粒子删除, 形成一个空心的类似球形的空间(类似于胞孔), 最后根据想要获得的形状删除不需要的SPH粒子(类似于线切割获得试件). 由于球形晶体颗粒的堆积是一个随机过程, 所以必须在几何模型中体现胞孔的随机性, 这也是泡沫铝细观结构多样性最重要原因之一.
数值模拟中利用离散元软件PFC3D, 采用比较符合实际的蒙特卡罗法和重力堆积法来获取随机堆积的颗粒球心坐标. 具体实施步骤如下
1) 利用离散元软件PFC3D, 采用蒙特卡罗法, 在x1≤x≤x2,y1≤y≤y2,z1≤z≤z2的空间内生成n个半径R=f(n)的小球, 如图 2(a) 所示;
2) 对小球施加重力, 小球在重力作用下开始堆积, 直至系统的不平衡力趋向于0, 即认为堆积的球体物理上是平衡的, 如图 2(b) 所示;
3) 为了使混合更加均匀, 对堆积体x轴正方向所在面施加一个持续时间为t的位移正弦波,f(x)=Asinωt, 以模拟振动混合, 同样地, 对另外两个面进行振动混合;
4) 对球体堆积系统的上表面施加一定压力使堆积体更加致密以模拟得到实际中的预制坯体, 其表观体积为V, 如图 2(c) 所示;
5) 提取小球的球心坐标和半径.

图 2 球体堆积过程Fig.2 Process of spheres accumulation
在获取球心坐标和半径后, 通过自编的前处理程序生成泡沫铝细观结构几何模型. K文件由MatLab生成, 以输入一个球心坐标和半径为例来介绍算法, 主要步骤流程见图 3, 图 4 为生成的开孔泡沫铝试件整体效果图.

图 3 生成K文件流程图Fig.3 Flowchart of generating K file

图 4 整体效果图Fig.4 Final view of the global model
基于上述流程所得的泡沫铝几何模型, 其相对密度为
(1)
式中:ρ*为泡沫铝密度;ρs为基体材料密度;n为小球个数;r为小球半径;V为预制坯体表观体积.
对于同一组颗粒的球心坐标, 采用粗略、 中等和细化三种不同细观程度的几何模型在1 000 s-1应变速率下进行计算, 所得到的几何模型参数如表 1 所示, 考虑到计算时间经济性, 本文中数值计算均采用中等SPH粒子数的几何模型.

表 1 几何模型参数
1.3材料模型
泡沫铝基体材料的本构选择理想弹塑性模型, 采用Cowper-Symonds模型来描述基体材料的应变率效应, 表达式为
(2)

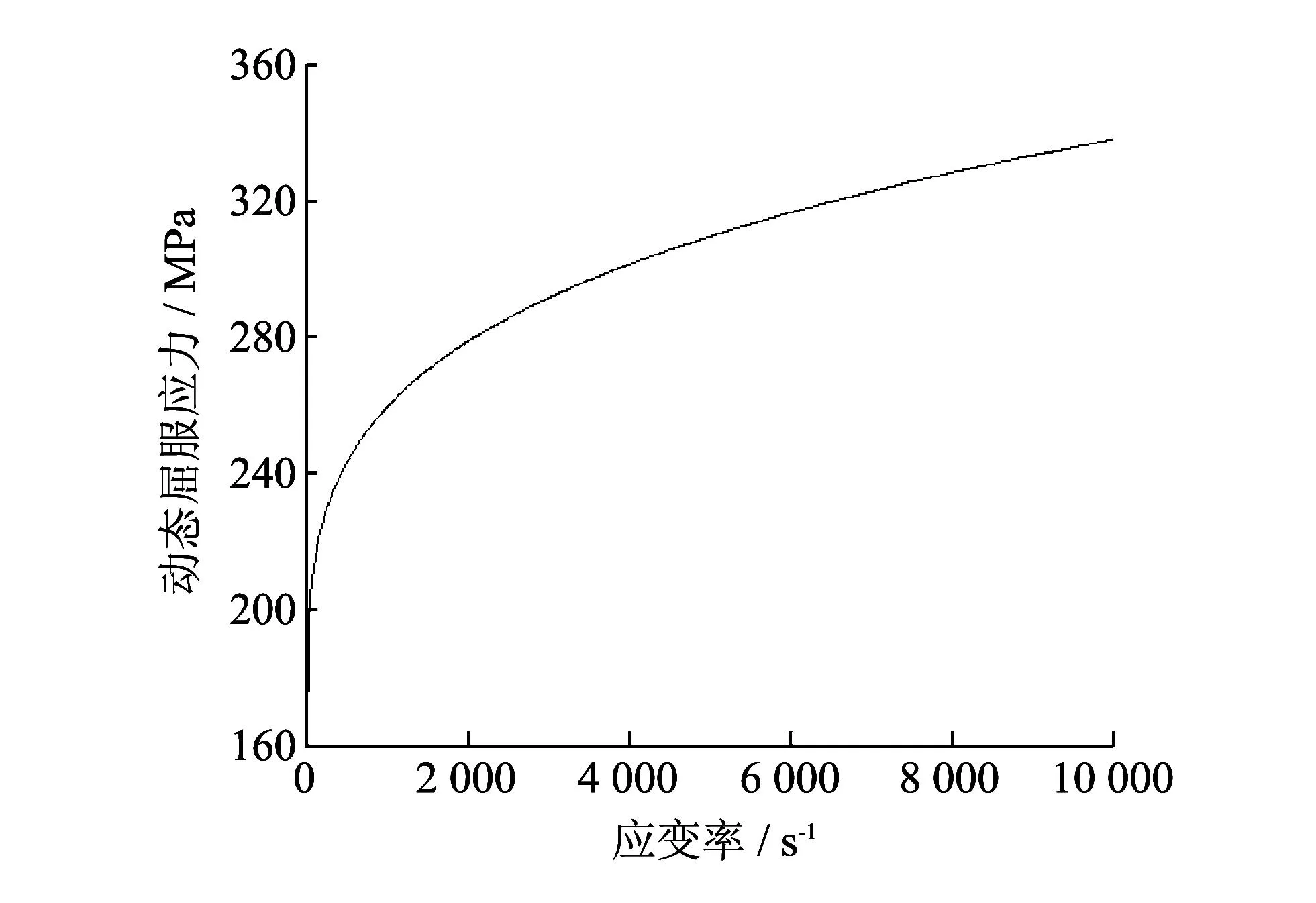
图 5 动态屈服应力与应变率的关系曲线Fig.5 Strain rate versus dynamic yield stress
2数值模拟结果
2.1应变率对力学性能的影响
为了研究应变率对开孔泡沫铝动态力学性能的影响, 在应变率范围为10~10 000 s-1内, 选取不同量级且有一定代表性的应变率进行压缩数值模拟, 其中低应变率为10, 100和500 s-1, 其代表环境为跌落、 车辆低速碰撞等, 中应变率为1 000 s-1和2 500 s-1, 其代表环境为汽车高速碰撞、 火车碰撞等, 高应变率为5 000 s-1和10 000 s-1, 其代表环境为动能型弹丸高速撞击、 爆炸产生的冲击波等.
图 6 为仿真所用的几何模型, 几何模型尺寸为Φ3.5 cm×3.5 cm, 平均孔径为4 mm, 相对密度为0.295.

图 6 几何模型示意图Fig.6 Schematic diagram of geometric model
几何模型两端各添加一块刚性墙, 下方为固定不动的刚性墙, 边界条件为固支约束, 上方是以恒定速率v压缩的加载面, 泡沫铝的应变率
(3)
式中:v为加载面的加载速率;h为泡沫铝几何模型沿加载方向上的尺寸, 本文中即几何模型高度.
根据所选取的应变率大小和所构建的几何模型高度, 恒定加载速率分别为0.35, 3.5, 17.5, 35, 87.5, 175和350 m/s.
图 7 为固定端的应力-应变曲线, 图中应力均指固定端面所受的力与圆柱形泡沫铝下端面表观面积之比, 应变均指泡沫铝的压缩量与原高度的比值.
通过分析固定端应力-应变曲线可知:在应变率范围为10~10 000 s-1内, 所建立泡沫铝模型的应力-应变曲线均表现出明显的三阶段特征, 即线弹性区、 塑性屈服平台区和致密区, 这与前人的结论相符[1,5]. 在中、 低应变率范围内(10~2 500 s-1), 泡沫铝模型的初始屈服应力和塑性平台区的流动应力均随应变率的增长而上升, 表现出明显的应变率效应. 但是在高应变率范围内(>2 500 s-1), 与中、 低应变率相比, 固定端面的应力-应变曲线的塑性平台区长度减小, 且表现出明显的滞后现象.

图 7 固定端应力-应变曲线Fig.7 Stress-strain curve of the fixed face
图 8 为压缩端的应力-应变曲线, 其同样表现出明显的应变率效应. 在应变率范围为10~2 500 s-1内, 应力-应变曲线较为平滑, 固定端与压缩端的应力-应变曲线相一致. 随着应变率的增大, 曲线的波动更加剧烈, 固定端与压缩端的应力-应变曲线的不均匀程度也随着增大.

图 8 压缩端应力-应变曲线Fig.8 Stress-strain curve of the compression face
2.2开孔泡沫铝的变形模式

在低应变率范围内, 泡沫铝孔结构整体受力比较均匀. ① 在线弹性阶段, 外力所做的功在泡沫铝承受范围之内, 不足以使之发生塑性变形, 这一阶段外力所做的功转化为泡沫铝的弹性势能, 沿压缩方向的胞孔棱杆主要表现为弹性弯曲, 平行于刚性墙的胞孔棱杆主要表现为弹性拉伸, 且沿压缩方向的胞孔棱杆的应力明显高于平行于刚性墙的胞孔棱杆. ② 当外力所做的功积累到一定程度时, 泡沫铝由线弹性阶段进入塑性屈服阶段. 由于泡沫铝胞孔空间排列的随机性与不均匀性, 塑性变形首先从最薄弱的一层开始, 此时薄弱层的胞孔棱杆主要表现为不可恢复的塑性弯曲和断裂, 导致局部层面上的胞孔被压溃, 形成表观上的变形带, 而非薄弱层的棱杆仍处于弹性阶段. 当外力继续做功, 原先的薄弱层不能产生更大的塑性变形以吸收额外的能量, 此时会产生新的薄弱层发生塑性变形以维持能量的平衡. 由于低应变率下泡沫铝会不断产生新的薄弱层, 并且压溃所需的应力较小且平稳, 所以泡沫铝能以较低的流动应力产生较大的塑性变形. ③ 随着外力做功继续增加, 泡沫铝被层层压溃, 直至进入密实化阶段. 密实化阶段胞孔已经完全坍塌, 孔洞被压实, 棱杆与棱杆之间相互约束, 此时泡沫铝更多的表现出基体材料的性质, 这导致密实化阶段泡沫铝产生微小的塑性变形需要大量的能量. 另外, 低应变率下泡沫铝在压缩过程中径向尺寸较初始状态略增大, 且应变越大, 径向的塑性延伸越明显.
与低应变率相比较, 高应变率下泡沫铝表现出截然不同的变形模式. ① 泡沫铝首先在压缩端形成一道较窄的变形带, 但是此时冲击波还未传播到靠近固定端的泡沫铝, 所以冲击阵面后方已经发生塑性变形, 而冲击阵面前方的区域未发生塑性变形, 这也解释了高应变率下固定端面的应力-应变曲线有明显的滞后现象, 且应变率越高, 滞后现象越明显. ② 随着压缩量的增大, 压缩端面的变形带也随着变宽, 且变形带的致密程度有所增加, 此时冲击波引起固定端面附近的泡沫铝产生塑性变形, 这在固定端应力-应变曲线上体现为固定端应力开始增加并形成一段平台区. 应变率较高时, 在固定端面附近的泡沫铝产生塑性变形之前, 压缩端面已经形成一段较厚的变形带, 由于冲击阵面前方可压缩的泡沫铝长度减小, 导致应力-应变曲线的平台区减小. ③ 当进入致密阶段后, 密实化的泡沫铝更多的表现基体材料的性质, 所以高应变率下泡沫铝的应力会急剧上升.

图 9 不同应变率下的应力云图Fig.9 Stress nephogram of distinctive strain rate
3结论
利用离散元软件PFC3D模拟了球形晶体颗粒的随机堆积过程, 提出了基于渗流法的开孔泡沫铝细观结构数值模拟方法, 并在应变率范围为10~10 000 s-1内进行了泡沫铝的单轴压缩数值模拟, 计算结果表明:
1) 基于渗流法的开孔泡沫铝细观结构数值模拟方法较真实地体现出泡沫铝胞孔空间排列的随机性, 利用SPH算法能够再现泡沫铝的动态压缩过程以及观察到内部胞孔的变形过程;
2) 随着应变率的上升, 其对泡沫铝的力学性能影响也越大. 中、 低应变率下, 固定端和压缩端的应力-应变曲线几乎一致, 但在高应变率下, 固定端面应力-应变曲线表现出明显的滞后现象, 固定端和压缩端面的动态响应存在较大差异;
3) 中、 低应变率下, 泡沫铝总是从最薄弱的一层开始坍塌, 而高应变率下, 泡沫铝从压缩端开始逐层坍塌.
参考文献:
[1]卢天健, 何德坪, 陈常青, 等. 超轻多孔金属材料的多功能特性及应用[J]. 力学进展, 2006, 36(4):517-535.
Lu Tianjian, He Deping, Chen Changqing, et al. The multi-functionality of ultra-light porous metals and their applications[J]. Advances in Mechanics, 2006, 36(4): 517-535. (in Chinese)
[2]程涛, 向宇, 李健, 等. 泡沫铝在汽车工业中的应用[J]. 轻金属, 2009, 42(8): 71-75.
Cheng Tao, Xiang Yu, Li Jian, et al. Application of aluminium foam in automotive industry[J]. Light Metals, 2009, 42(8): 71-75. (in Chinese)
[3]梁增友, 高位, 陈智刚. 泡沫金属/金属管塑性变形缓冲器降低弹载设备过载的数值模拟[J]. 兵工学报, 2013, 34(8): 1041-1045.
Liang Zengyou, Gao Wei, Chen Zhigang. The numerical simulation of metal foam/metal tube plastic deformation energy absorber for reduction in overload of projectile-borne equipment[J]. Acta Armamentarii, 2013, 34(8): 1041-1045. (in Chinese)
[4]Davies G J, Shu Z. Metallic foams: their production, properties and applications[J]. Journal of Materials Science, 1983, 18(7): 1899-1911.
[5]Gibson L J, Ashby M F. Cellular solids: structure and properties(second edition)[M]. London: Cambridge university press, 1997.
[6]Zhu H X, Knott J F, Mills N J. Analysis of the elastic properties of open-cell foams with tetrakaidecahedral cells[J]. Journal of the Mechanics and Physics of Solids, 1997, 45(3): 319-343.
[7]Zhu H X, Mills N J, Knott J F. Analysis of the high strain compression of open-cell foams[J]. Journal of the Mechanics and Physics of Solids, 1997, 45(11): 1875-1904.
[8]Ahmed S S, Nihad D. Long-domain simulation of flow in open-cell mesoporous metal foam and direct comparison to experiment[J]. Microporous and Mesoporous Materials, 2014, 196(9): 104-114.
[9]Tekoglu C, Gibson L J, Pardoen T, et al. Size effects in foams: Experiments and modeling [J]. Progress in Materials Science, 2011, 56(2): 109-138.
[10]王长峰, 郑志军, 虞吉林. 泡沫杆撞击刚性壁的动态压溃模型[J]. 爆炸与冲击, 2013, 33(6): 587-593.
Wang Changfeng, Zheng Zhijun, Yu Jilin. Dynamic crushing models for a foam rod striking a rigid wall[J]. Explosion and Shock Waves, 2013, 33(6): 587-593. (in Chinese)
[11]Li Zhiqiang, Zhang Jianjun, Fan Jianhui, et al. On crushing response of the three-dimensional closed-cell foam based on Voronoi model[J]. Mechanics of Materials, 2014, 68: 85-94.
[12]Saenger E H, Uribe D, Jänicke R, et al. Digital material laboratory: Wave propagation effects in open-cell aluminium foams[J]. International Journal of Engineering Science, 2012, 58: 115-123.
[13]陈鹏. 泡沫铝夹芯结构力学性能研究[D]. 哈尔滨: 哈尔滨工业大学, 2013.
[14]邹毅, 何德坪, 蒋家桥. 新型球形孔低孔隙率高强度泡沫铝合金[J]. 中国科学, 2004, 34(2): 168-176.
Zou Yi, He Deping, Jiang Jiaqiao. New type spherical hole aluminum foam with low porosity and high strength[J]. Science in China, 2004, 34(2): 168-176. (in Chinese)
[15]Su X Y, Yu T X, Reid S R. Inertia-sensitive impact energy absorbing structures: prat Ⅱ, effect of strain rate[J]. International Journal of Impact Engineering, 1995, 16(4): 673-689.
Research on Micro Structural Model of Open-Cell Aluminum Foam Based on Infiltration Casting Methods
FENG Yang1,2, LIANG Zeng-you1,2, WU Hong-chao1,2, CHEN Zhi-gang1,2
(1. School of Mechatronics Engineering, North University of China, Taiyuan 030051, China;2. National Key Laboratory of Underground Damage Technology, Taiyuan 030051, China)
Abstract:Aluminum foam is an excellent energy absorption material which can produce large plastic deformation at low flow stress. Infiltration casting method is one of the mature methods of producing open-cell aluminum foam industrially. Based on the technological process of this method, a micro structural model of open-cell aluminum foam was built by Monte Carlo method and gravitational sedimentation method. Combined with SPH algorithm, compression behavior of aluminum foam was studied numerically from low strain rate 10 s-1to high strain rate 10 000 s-1. Then deformation and failure mode was analyzed. The results show that the numerical simulation method based on the infiltration casting methods of manufacturing open-cell aluminum foam can reproduce the dynamic compression process and compared to middle and low strain rate, there is a significant difference of deformation and failure mode at high strain rate.
Key words:open-cell aluminum foam; micro structure; infiltration casting methods; numerical simulation
中图分类号:O341
文献标识码:A
doi:10.3969/j.issn.1673-3193.2016.01.017
作者简介:冯阳(1991-), 男, 硕士生, 主要从事战斗部结构设计及高效毁伤技术研究.
*收稿日期:2015-06-19
文章编号:1673-3193(2016)01-0090-07

