探究式教学对高等数学教学质量影响的评价
李亚男,王玉光
(1.河南理工大学 万方科技学院,河南 焦作 454000;2.宁夏大学 数学计算机学院,宁夏 银川 750021)
探究式教学对高等数学教学质量影响的评价
李亚男1,王玉光2
(1.河南理工大学 万方科技学院,河南 焦作 454000;2.宁夏大学 数学计算机学院,宁夏 银川 750021)
在高等数学教学中引入探究式教学,评价其对学生成绩的影响.分析实验班和对照班经过1个学期教学改革后学生考试成绩的变化,利用时间效益分析方法和显著性检验得到实验班的成绩较对照班成绩有明显提高的结论.
探究式教学;高等数学;质量评价;时间效益分析
高等数学作为高等院校尤其是工科院校的基础课程之一,在整个学生培养方案中起着重要作用.目前高校中高等数学课程的授课普遍存在着教师按统一标准授课,不考虑学生基础水平和接受能力,重知识逻辑轻应用实践现象,与学生的培养目标不相符,与当前倡导的素质教育实质相违背.探究式教学[1-5]以问题为导向,通过分析找出解决问题关键,进而构建相应理论知识,实现问题的求解,既让学生了解知识产生的背景,又使其掌握了解决问题的方法,在教学过程中逐渐培养学生的实践能力和科研能力.
1 时间效益分析方法的基本步骤
可以利用时间效益分析法计算不同等级的学生达到预定等级(如优秀)需要的教学时间期望,期望值越小表示教学效果越好[6].
时间效益分析方法基本步骤为:
Step1 确定学生成绩等级.
Step2 制作成绩转移表(见表1),其中:A,B,C,D,E分别表示优秀(等级1)、良好(等级2)、中等(等级3)、及格(等级4)和不及格(等级5);ij表示第1次成绩为等级i,第2次成绩为等级j.

表1 成绩状态转移
Step4 计算矩阵B=I−G的逆矩阵.
Step5 求出每个学生达到期望等级的期望时间.具体做法为将中按i对应的行相加,即可得到i等级达到期望等级(优秀)的期望时间.
2 具体实施过程
以河南理工大学万方科技学院电气系2013级电气专业278名学生为例,实验班为151人,对照班为127人,实验班采用探究式教学,对照班仍采用按统一标准授课的模式.
2.1 确定学生成绩等级
按标准正态分布从-2.5到+2.5的区域占总面积的98.76%,因此以长度1为单位将-2.5到+2.5分成5个区间,其余部分合至两侧,得到各等级学生占的比例,即优秀:P(Z>1.5)=0.066 81;良好:P(0.5 2.2 成绩状态转移表 按照表1格式要求,制作学生成绩标准等级转移情况表(见表2). 表2 实验班和对照班成绩状态转移表 2.3 列出学生群体变化的转移矩阵 根据公式aij=ij出现的频数出现的频数,确定实验班和对照班学生群体成绩转移矩阵分别为 2.4 确定等级期望 由Z1,Z2得到G1,G2,利用Matlab计算矩阵的逆矩阵,得 表3 实验班和对照班各等级期望 学期 由此,可求得2个教学班学生达到预定目标的期望时间. 由第2等级到第1等级的人数为ij= 22,23,24,25人数之和,实验班的人数为18,对照班的人数为6;由第3等级到第1等级的人数为ij= 32,33,34,35人数之和,实验班的人数为21,对照班的人数为12;由第4等级到第1等级的人数为ij= 42,43,44,45人数之和,实验班的人数为22,对照班的人数为24;由第5等级到第1等级的人数为ij= 52,53,54,55人数之和,实验班的人数为53,对照班的人数为64. 用对数一致性比率进行显著性检验[7-8],统计量为,其中:x(o)为观察值;x(e)为理论值.理论值为实验班数值乘以对应人数加上对照班数值乘以对应人数,除以2组学生总人数,实验班和对照班各等级达到目标的总体期望值(理论值)分别为3.059 4,3.958 6,4.653 8,4.633 8学期. 将相应数据代入检验统计量公式,得2I=35.302 9.该统计量的临界值为7.815(自由度df=4-1=3,显著性水平alpha=0.05),观察值35.302 9大于临界值7.815,不能认为这2个班级的成绩来自于同一个样本.因此,这一差异确实是由于教学质量不同引起的.由表3可以看出,实验班的学生达到预期目标的期望时间小于对照班,可以认为实验班的教学质量要高于对照班. 探究式教学可以显著提高教学质量,对学生实践能力的培养与倡导的素质教育是相一致的,评价方法可用到其它教学质量评价上[9-10],也能够在学校的教学管理中对教学单位的人员或教学改革方法模式进行教学质量评估排序. [1]张新华,毕雁.高等数学探究式教学及SWOT分析[J].长沙铁道学院学报:社会科学版,2014(3):207-208 [2]章劲鸥.高等数学探究式教学案例研究——基于“定积分的概念”的教学设计[J].宁波教育学院学报,2015(1):55-57 [3]栾丹.高等数学探究式课堂教学模式探索与研究[J].辽宁师专学报:自然科学版,2015(1):5-7 [4]安黔江.高等数学探究式教学模式及其评价分析[J].兰州教育学院学报,2014(1):100-101 [5]魏更春,陆竞,赵丽艳.高等数学“探究式”教学模式评价模型分析[J].黑龙江科技信息,2014(22):37 [6]张敏,朱晖.探究式教学模式的高等数学教学质量评价[J].数理医药学杂志,2012(4):496-497 [7]杨金云.探究式教学法在高等数学中的应用[J].徐州教育学院学报,2008(3):122-124 [8]杨宪立,张环理.在高等数学中开展探究性教学的实验研究[J].河南教育学院学报:自然科学版,2014(2):62-65 [9]魏妙.探究式教学在高等数学教学中的实践[J].陕西教育:高教版,2011(9):102 [10]陈文英.论高等数学探究式教学中的问题情境创设[J].高等理科教育,2009(4):43-45 Quality evaluation of inquiry teaching′s impaction on advanced mathematics LI Ya-nan,WANG Yu-guang (1.Wanfang Institute of Science and Technology,Henan Polytechnic University,Jiaozuo 454000,China;2.School of Mathematics and Computer Science,Ningxia University,Yinchuan 750021,China) By introducing the inquiry teaching in advanced mathematics,the evaluation of effects on achievement are obtained.Comparing the scores between experimental classes and comparative classes after one semester,using the method of time efficiency analysis and significance test experimental,get the result that the improvement is obviously in experimental classes than comparative classes. inquiry teaching;advanced mathematics;quality evaluation;time efficiency analysis O175∶G642.0 A 10.3969/j.issn.1007-9831.2016.12.019 2016-05-31 河南省教育厅重点项目(17B110004);河南理工大学万方科技学院教改项目(WFJG2016005) 李亚男(1983-),男,河南焦作人,讲师,硕士,从事生物数学研究.E-mail:lyn@hpu.edu.cn 王玉光(1983-),男,河南南阳人,讲师,硕士,从事基础数学研究.E-mail:270238001@qq.com 1007-9831(2016)12-0072-03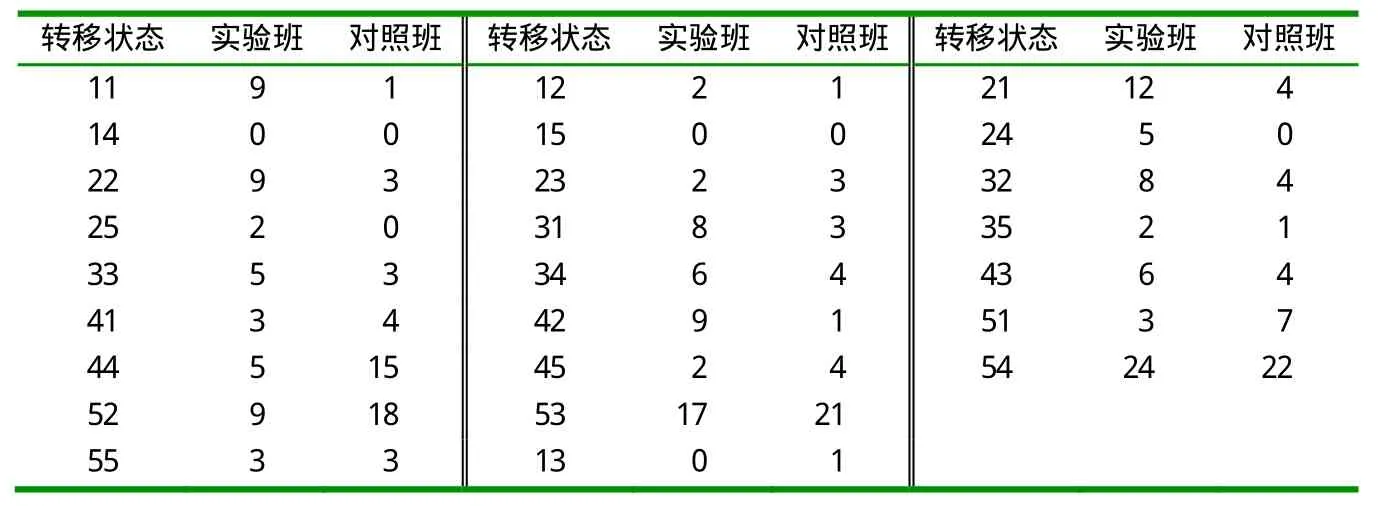



3 显著性检验

