基于SVM的高校录取分数预测模型

李诚，张宏烈，王崇

（齐齐哈尔大学 计算机与控制工程学院，黑龙江 齐齐哈尔 161006）

基于SVM的高校录取分数预测模型

李诚，张宏烈，王崇

（齐齐哈尔大学 计算机与控制工程学院，黑龙江 齐齐哈尔 161006）

由于随机性大，影响因素多，导致高校录取分数预测困难，准确度不高，相关研究较少.针对这种情况，尝试基于支持向量机（SVM）理论，结合我国高考录取模式，建立SVM模型对高校录取分数进行初步预测.通过对预测结果的定量分析，证明预测效果较理想，预测的平均绝对误差为7.6分，同时验证了SVM预测模型在高校录取分数预测中的可行性.

支持向量机；定量分析；预测模型

高考是进入理想大学学习的必经途径，也是历年来社会关注的一个焦点.通常，考生填报志愿的时候大多都是依靠老师或者家长的经验和自己的理解.但是仅凭人为的经验去解决考生的志愿填报是非常不准确的，一方面是老师和家长掌握的资源十分有限，分析不可能十分全面；另一方面老师和家长对历史录取情况的理解主观因素会比较多.因此，如何找到适合于自己分数的高校是一个难点问题.

高校录取分数的划定受招生政策、招生规模、报考人数、考生素质、历年线差和学校知名度等许多因素共同影响，随机性较大.目前，相关研究分3类：考生高考成绩预测[1]165，高校招生情况预测[2-3]及高考志愿决策支持系统[4-5].使用的相关技术为神经网络[1]164、灰色模型[3]48-49、决策树[6-7]和支持向量机[8-9]等，而对某一所高校或者一些高校的录取分数预测的研究非常少.本文尝试基于SVM理论，结合我国高考录取模式，建立SVM模型来对高校录取分数进行初步预测，同时要验证SVM预测模型在高校录取分数预测中的可行性.

1 支持向量机

支持向量机（support vector machines，SVM）是Vapnik等设计的一种机器学习算法，其基本思想是依据统计学习理论，利用核函数将输入样本空间映射到高维特征空间，在这个高维空间中求得一个最优分类面，得到输入与输出变量间的非线性关系[10].支持向量机是一个凸二次优化问题，得到的解是全局最优解，它适合解决小样本、非线性和高维模式识别等方面的问题，并能够推广应用到函数拟合等其它机器学习问题中.

在支持向量机（非线性）算法中，设给定训练样本为

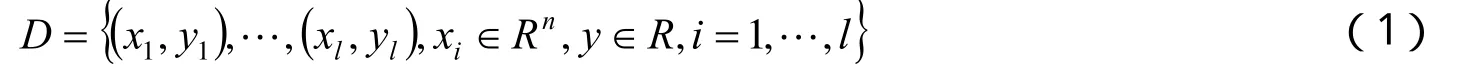
存在一个分类面即超平面，其方程为

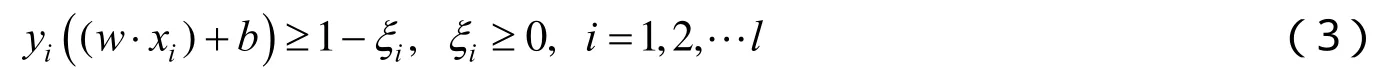
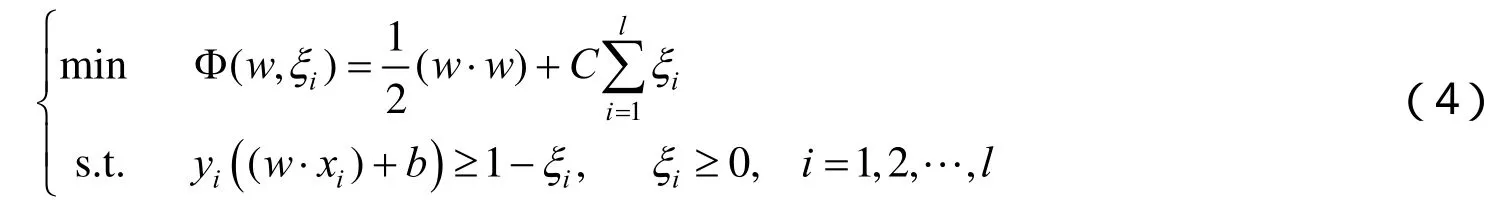
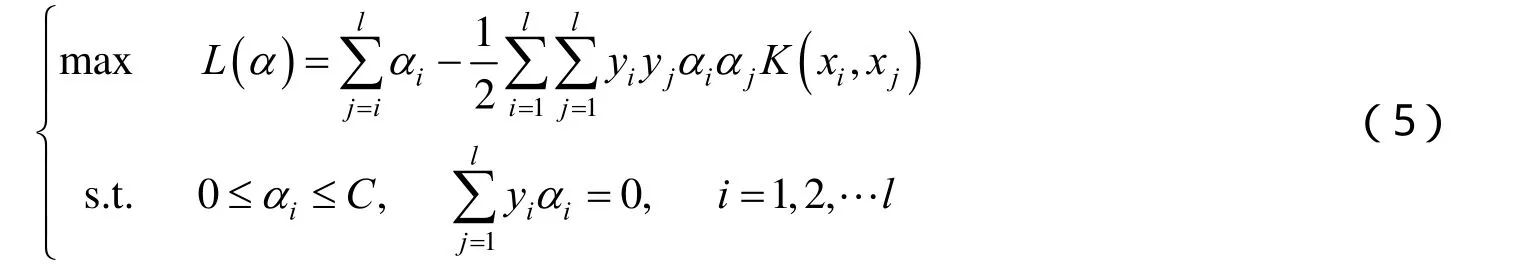
根据式（5）得到非线性分类问题的判别函数为

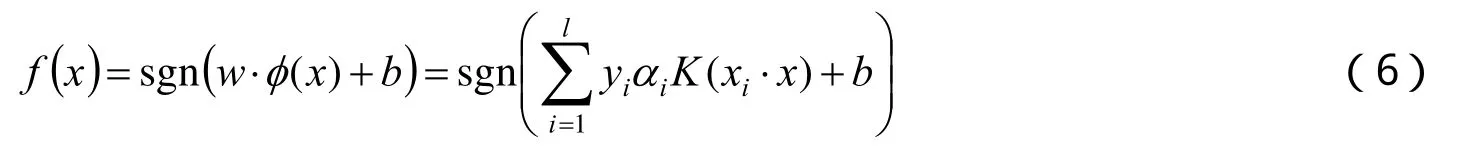
根据式（6）就可以判断x所属的类别了，也就是预测x的值.

2 高校录取分数预测

2.1 预测建模

高校录取分数预测的训练集中可能会出现“野点子”，就是偏远点，可能会对最终的分类超平面产生严重的影响，所以在SVM模型中加入一个松弛变量，将约束放宽.预测的结果不能保证是线性分类，所以模型使用非线性SVM，使用核函数将变量映射到高维空间，这样的核函数必须满足Mercer条件，所以本研究中的核函数选择高斯核

其中：核参数g的值与式（4）中惩罚参数C的值，都是先验值，或说实验值.就是说，在实验中，反复修改这2个参数值，选择效果好的值.本模型多次实验后选择

2.2 数据样本

黑龙江省2013年实行平行志愿，本仿真实验以2013—2016年随机选取的10所高校在黑龙江省招收一本理科生的最低分数为样本数据（见表1），其中，2013—2015年数据为训练样本，2016年数据为测试样本.

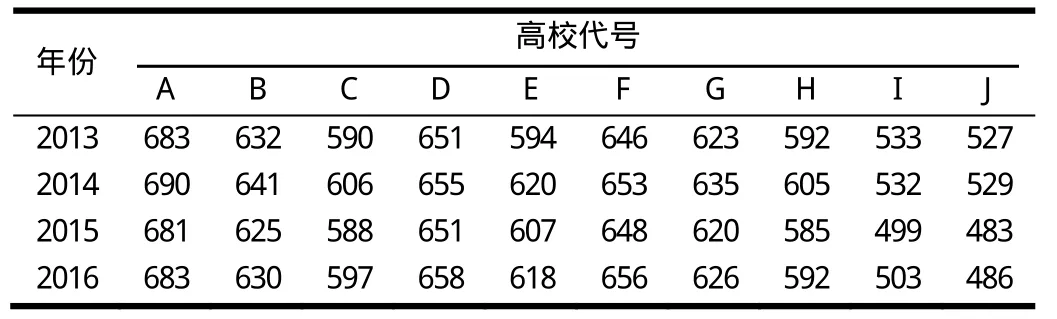
表1 数据样本

2.3 预测结果分析

2013—2015年数据被用来训练已建立的模型（由于数据样本过少，预测相对误差大，另加2013—2016年省控线训练数据），预测2016年这10所高校的最低录取分数.然后预测分数与2016年的真实数据进行对比检验，计算相对分数差（真实分数-预测分数）.最后采用平均绝对误差（MAE）对本文预测模型效果进行评价.预测仿真实验使用安装了Libsvm-3.21工具包的MATLAB R2010b软件完成.

预测结果见表2.

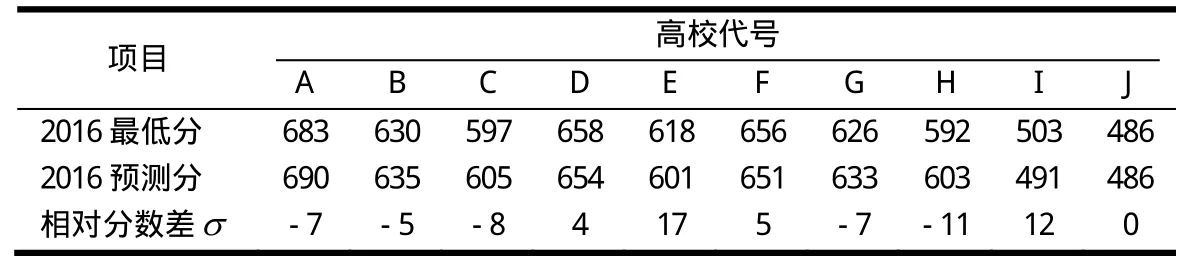
表2 预测结果

使用MAE对预测效果评价

由表2可知，只是在少数预测点的相对预测误差较大，大部分预测点的相对预测分数差都较为理想，且MAE仅为7.6分，这个预测结果比较理想，从而验证了支持向量机在高校录取分数预测中的可行性.

3 结论

支持向量机最大优势是能够运用于小样本条件下的机器学习.本文选用各高校历年录取最低分数线数据，基于支持向量机理论，来建立高校录取分数预测模型对下一年高校录取分数最低线进行预测.通过对预测结果的定量分析，证明预测效果较理想，同时验证了SVM预测模型在高校录取分数预测中的可行性.完善模型、预测结果定性分析及提高预测精度将是本文后续研究的一个方向.后续研究的另一个方向为高校专业录取分数的预测，大部分考生更看重高校热点专业录取分数，这与社会因素密不可分，具有更大的实用价值.

[1]武剑平.基于BP人工神经网络的学生高考成绩预测[J].科技传播，2015（20）：164-165

[2]于继江.一种改进离散灰色模型及其高校招生人数预测建模[J].高师理科学刊，2010，30（2）：46-49

[3]郭海如，万兴，吴朋飞.基于灰色理论的高校招生人数预测[J].湖北工程学院学报，2013，33（6）：48-51

[4]徐刚强，林燕.基于数据挖掘的招考志愿填报辅助决策支持系统[J].计算技术与自动化，2014，33（4）：106-109

[5]铁鑫.基于数据挖掘技术的高职学院招生决策支持系统研究[J].信息与电脑：理论版，2010（6）：137-138

[6]苗煜飞，张霄宏.决策树C4.5算法的优化与应用[J].计算机工程与应用，2015，51（13）：255-258

[7]代昆玉，胡滨.决策树算法在高考志愿填报中的应用[J].贵州大学学报：自然版，2009，26（2）：71-73

[8]程双江，李世平，邬肖敏，等.基于改进混合核 SVM的非线性组合预测[J].计量技术，2015（10）：3-7

[9]李建萍.基于加权支持向量机的学习成绩预测模型[J].中国科教创新导刊，2009（14）：137-138

[10]丁世飞，齐丙娟，谭红艳.支持向量机理论与算法研究综述[J].电子科技大学学报，2011，40（1）：2-10

Prediction model for college admission score based on SVM

LI Cheng，ZHANG Hong-lie，WANG Chong

（School of Computer and Control Engineering，Qiqihar University，Qiqihar 161006，China）

The college admission score prediction is with the high difficulty，the low accuracy and the less related research，because of its high randomicity and multiple influencing factors.Aiming at the situation，based on the support vector machine（SVM）theory，the prediction model for college admission score is constructed to carry out the preliminary prediction，which is combined with the admission mode of Chinese college entrance examination in the paper.By the quantitative analysis of the prediction results，the ideal prediction effect is achieved，the mean absolute prediction error is 7.6，and the feasibility of the SVM prediction model is verified for college admission score prediction.

support vector machine（SVM）；quantitative analysis；prediction model

TP274

A

10.3969/j.issn.1007-9831.2016.12.005

2016-10-15

齐齐哈尔市科技局工业攻关计划项目（GYGG-201408）

李诚（1978-），男，黑龙江齐齐哈尔人，副教授，从事嵌入式系统和人工智能等研究.E-mail：lcrb406@163.com

1007-9831（2016）12-0022-03