基于投资组合优化与条件极值的数学实验案例设计

高丽，韩乐，姚占林

（华南理工大学 数学学院，广东 广州 510641）

基于投资组合优化与条件极值的数学实验案例设计

高丽，韩乐，姚占林

（华南理工大学 数学学院，广东 广州 510641）

将金融和社会经济活动领域受到高度关注的投资组合优化模型和条件极值问题引入到数学实验课程中，设计难宜适中的数学实验案例.借助MATLAB语言编程，将数学理论工具应用于经济实践中以解决实际问题，激发了学生的研究兴趣和探索欲望，既实现了教学与科研的资源共享，又丰富了数学实验课程的教学内容.

投资组合；均值-方差模型；条件极值；数学实验

数学实验作为一种新的教学模式，其主要目的是引导学生进入做数学的境界，激发学生动手和探索的兴趣[1]，数学软件的学习与使用也将是数学实验的主要内容[2].学生可以借助计算机实现实验设计，分析和解决一些经过简化的实际问题，从而体验应用数学知识解决实际问题的过程[3].数学实验强调学生自己动手，利用计算机和数学软件，从问题情境出发（实际问题或数学问题），在教师的指导下，进行探索性实验，建立数学模型，设计求解方法，提出猜想并进行证明或验证，从而使学生的数学思维和创新能力得到有效的训练和提高[4-6].数学实验的案例设计可以结合学生的专业知识和教师的科研特长，丰富数学实验的教学内容，拓宽学生的视野，与时俱进，为未来的科学研究打下良好的基础.目前，数学实验案例的选取和内容的设计多偏重于理工类经典问题，相对缺少大多数学生感兴趣的金融类热点案例.

本文利用现有教学资源与科研平台，抛开数学实验的经典问题，将在金融优化领域中受到高度关注的投资组合优化模型与条件极值问题[7-8]引入到数学实验中，设计难度适中的案例，并用MATLAB[9-10]编程实现.该实验案例的实施，为学生提供了接触并了解数学应用和金融优化的平台，引导和鼓励学生利用计算机技术和数理知识与方法解决社会关注的金融问题.这样既可以让本科生及时了解数学的具体应用，拓宽他们的知识面，提高其数学的应用能力，又可以激发学生的探知欲，实现教学与科研的资源共享，使教学与科研相互促进.

1 投资组合优化问题介绍

1952年，美国经济学家Harry Markowitz发表了论文Portfolio Selection[11]，从而奠定了现代投资组合的理论基础[12].Harry Markowitz对证券市场的最佳投资问题进行了开创性的研究，详细地论证了证券收益和风险的主要原因和分析方法，提出的均值-方差（Mean-Variance）理论为风险和收益的权衡提供了可行的量化方法，是现代投资组合理论的开端，在此基础上开展了大量的研究，目前依然是金融领域的研究热点[13-14].基于均值-方差模型在现代金融理论中的重要性，本文以经典的均值-方差模型为基础，设计和探索条件极值在实际中如何应用的数学实验.

在均值-方差模型中，用均值度量收益，用方差度量风险.众多的事例表明，绝大多数投资者都是风险趋避者.投资者追求较高的预期收益，但他们一定都希望避免带来风险.降低风险的方法就是不要把资金全部放在一种收益和风险都高的证券上，而是分散地投在若干收益和风险不同的证券上，这样可以使总体风险降下来，降低到投资愿意或可以接受的水平，或者在可以接受的收益水平下达到风险最小.简而言之，投资组合决策方法是在预期收益给定的条件下，最小化风险；或者在风险给定的条件下，最大化期望收益.

假如从金融市场上已经选出了N种证券，xi表示投资到第i种证券的价值比率，即权数；p表示由这N种证券构成的一个证券组合；表示第i种证券的收益率；rp表示证券组合p的收益率.由于受金融市场波动及投资者个人理财行为等多种因素的影响，和rp一般呈现随机变化.进一步假设为证券组合p的资金投资比例系数向量（即权重向量），也称为一个投资组合；为证券组合投资的收益率向量；为r的期望向量，即N.定义期望收益率；证券组合投资的风险

基于以上假设，Markowitz 投资组合的均值-方差模型可描述为如下2种基本形式的规划模型：

（1）给定期望收益水平的最小化风险模型

其中：r0为证券组合的预期收益率；

（2）给定风险水平的最大化收益模型

2 案例设计与实施

对于一个理性的投资者而言，他们都是厌恶风险而偏好收益的.对于相同的预期收益率，他们会选择风险最小的组合；对于相同的风险水平，他们会选择能提供最大收益率的组合.能同时满足这2个条件的投资组合就是有效集（efficient set），又称有效边界、有效前沿（efficient frontier）.处于有效边界上的组合称为有效组合（efficient portfolio）.

例 从Wind数据库中选取了中国股票市场2014-01-02至2016-02-25共523个交易日中5只股票（启明星辰002439，太安堂002433，新湖中宝600208，盛和资源600392，林洋电子601222）的前复权开盘价与收盘价数据，要求使用MATLAB软件编程找出有效组合曲线以及相对应的投资组合策略，并判断有效组合曲线轨迹的特点.

本组40例患者发现病灶40处，均表现为单发，其中右肺18例、左肺22例。直接征象：空洞（呈厚壁或薄壁）、肿块（边界清晰或不清晰，呈类圆形或不规则）、磨玻璃征（密度影略高，边界不清晰）；间接征象：分叶征（≥1个弧形突起存在于肿瘤边缘）、血管集束征、胸膜凹陷（同肿块相连的线性影像或小三角形影像）、毛刺征（呈短细线条状影，肿块边缘分布呈放射状）等，此外还存在胸腔积液、支气管气象征、空泡征、血管集束征、棘状突起等。

问题分析 有效组合问题可以化为模型（1）和模型（2）的求解问题.事实上，Markowitz投资组合的均值-方差模型就是一个多元条件极值问题.表达式（1）中的最小化风险即为最小化目标函数，收益和权重为约束条件；表达式（2）中最大化收益即为最大化目标函数，风险和权重为约束条件.

撇开具体问题，抽象出数学的一般方法.一般地，寻求目标函数

在条件约束

下取得极值的必要条件.

拉格朗日乘子法是解决条件极值的一般方法，引入拉格朗日函数，极值的必要条件化为求解方程组

方程组（5）即为拉格朗日函数关于变量x，y和λ求一阶偏导为零.解方程组（5）即可得到函数在条件约束下的可能极值点.

在拉格朗日乘子法基础上扩展得到了广义化的方法，称为KKT（Karush-Kuhn-Tucker）条件.在求取有约束条件的优化问题时，拉格朗日乘子法（Lagrange Multiplier）和KKT条件是2种非常重要的方法.对于等式约束的优化问题，可以应用拉格朗日乘子法去求取最优值；对于含有不等式约束的优化问题，可以应用KKT条件去求取.拉格朗日乘子法（Lagrange Multiplier）和KKT条件求得的结果只是必要条件，只有在目标函数为凸函数的情况下，才能保证是充分必要条件.

（3）计算向量X和Y的协方差，并返回ExpCovariance中.

通过MATLAB中的函数求得收益率均值与协方差矩阵（见表1和表2）.

表1 5只股票的收益率均值

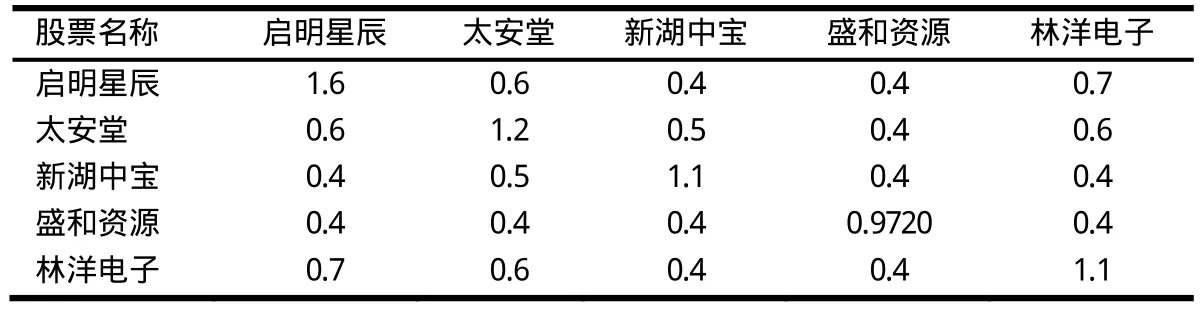
表2 5只股票的收益协方差矩阵×10-3

（4）求解约束条件下有效前沿的函数可使用Frontcon函数 [PortRisk，PortReturn，PortWts]=frontcon（ExpReturn，ExpCovariance，NumPort），Frontcon函数的各参数含义见表3.

表3 Frontcon函数的各参数含义

本实验取30个投资组合，即NumPort=30，由Frontcon函数，求得各个投资组合的风险、收益率（见表4）与各股比例（见表5）.

表4 投资组合的风险与收益率

表5 投资组合的权重

（5）利用画图命令plot（PortRisk，PortReturn，'r+ -'），可以得出有效前沿（见图1）.

案例分析

由图1可以看出，以标准差为风险度量的均值-方差模型有效前沿的基本形状为一条单调增的凹形曲线.

投资决策的核心问题是收益和风险之间的权衡.如果2个决策会带来相同的预期收益但要承受不同的风险，那么，风险大的那个决策是应该摒弃的；反之，如果承受相同的风险而有不同的预期收益，那么，预期收益小的那个决策也不是好的决策.投资者在高收益和低风险低收益之间，按照自己对收益和风险的偏好进行权衡和选择.在实际操作中，可以参考图1的有效前沿，根据投资者的偏好，选择合适的投资组合配置.分析数据可见，当保守的投资者选择风险最小为 0.024 3时，得到的投资组合收益为0.001 6，相应的策略为表5中的第1个策略：0.086 7，0.135 1，0.251 6，0.331 5，0.195 1，当投资者选择收益最大为0.003 4时，面临着投资组合风险为0.038 7，相应的投资组合策略为表5中的最后一个策略：1.000 0，0，0，0，0.

图1 以标准差为风险度量的均值-方差模型的有效前沿

3 结语

在金融市场中投资者在高风险高收益和低风险低收益之间，按照自己对收益和风险的偏好进行权衡和选择.投资组合选择就是如何配置各种有价证券的比例来最好地符合投资者对风险和收益的权衡.在该案例中，学生可利用拉格朗日乘子法的思想，根据收益和风险的不同取值进行条件极值的运算和模拟，以寻求满足不同投资需求的最优方案.从案例的实施过程中理解条件极值问题和拉格朗日乘子方法的理论与应用，并将金融理论专业知识灵活运用于金融实践操作中.

本文以金融模型为基础，以数学工具的运用为核心设计实验案例.通过软件编程，引导学生探索专业研究前沿，活学活用，激发学生研究兴趣，培养创新能力，以期能够做到教学、实验和应用三者的有效结合，培养出社会发展需要的高素质应用型人才，真正实现科研与教学相长.

[1]陈孝国，朱捷.依托大学数学实验，全面提高数学素质和数学能力[J].高师理科学刊，2011，31（2）：21

[2]李医民，王学弟，丁丹平，等.数学素质教育改革的系统工程[J].大学数学，2003，19（4）：34-37

[3]高文华，韩乐，刘元昌.基于随机微分方程Simulink 仿真的数学实验设计[J].高师理科学刊，2015，35（10）：62-65

[4]韩乐，高丽.基于压缩感知和稀疏优化的数学实验案例设计[J].高师理科学刊，2014，34（4）：34-36

[5]赵秀影，魏静元，全吉成，等.数学实验在工程数学教学中的应用[J].大学数学，2013，29（6）：95-98

[6]吴晓.大学数学中的数学实验教学[J].大学教育，2014（5）：116-117

[7]梅顺治，刘富贵，许桂水，等.高等数学方法与应用[M].北京：科学出版社，2001

[8]同济大学应用数学系.高等数学[M].6版.北京：高等教育出版社，2008

[9]魏鑫.MATLAB R2014a 从入门到精通[M].北京：电子工业出版社，2015

[10]张志涌.精通MATLAB6.5版[M].北京：北京航空航天大学出版社，2006

[11]Markowitz M H.Portfolio selection[ J].Journal of Finance，1952（7）：77- 91

[12]Markowitz M H.Foundation of Portfolio Theory [J].Journal of Finance，1991（2）：469-477

[13]张卫国.现代投资组合理论-模型、方法与应用[M].北京：科学出版社，2007

[14]杨海明，王燕.投资学（现代经济管理学教科书系列）[M].上海：世界出版集团上海人民出版社，2005

The design of a mathematical experiment based on portfolio optimization and conditional extremum

GAO Li，HAN Le，YAO Zhan-lin
（School of Mathematics，South China University of Technology，Guangzhou 510641，China）

A mathematical experiment was presented on portfolio optimization and conditional extremum，which are widely used in the finance and socio-economic activity.Designs the mathematical experiment which was moderate in terms of difficulty，the mathematical theory as a tool was applied to economic practice by MATLAB language，which motivated the students' desire and interest of exploration among concrete practices.The design of this experiment implements the resource sharing of teaching and research and also enriches the teaching content of mathematical experiment course.

portfolio；mean-variance model；conditional extremum；mathematical experiment

O29∶F830

A

10.3969/j.issn.1007-9831.2016.12.004

2016-09-27

广东省高等教育教学研究和改革项目——经管类和电信类交叉探索性数学案例教学改革研究；华南理工大学实验教学改革项目（Y1140730）——经管类探索性数学实验案例教学研究；广东教育教学成果奖（高等教育）培育项目——具有专业特色的数学实验研究型教学探索与实践

高丽（1978-），女，河南周口人，讲师，博士，从事金融优化计算研究.E-mail：gaoli@scut.edu.cn

1007-9831（2016）12-0017-05