关于求直线斜率方法的探讨
◆金玉国
(辽宁省阜新市第一中等职业技术专业学校)
关于求直线斜率方法的探讨
◆金玉国
(辽宁省阜新市第一中等职业技术专业学校)
在解析几何中直线方程的确定是十分重要的,而斜率又是确定直线方程的关键。结合教学经验,总结了关于求直线斜率方法的问题。
直线斜率 定义法 公式法 斜截式 向量 导数 点差法 待定系数法
在解析几何中,直线方程的确定是十分重要的,而斜率又是确定直线方程的关键。下面结合笔者多年的教学经验,总结一下关于求直线斜率方法的问题。
一、定义法:利用定义k=tanα(α≠900)求斜率
例1.如图正三角形OAB求两边OA、OB所在直线的斜率。

解:∵在正三角形中∠AOB=600∠ABO=600
∴直线AO的倾斜角为600AB的倾斜角为1200
点评:此类问题的解答关键是确定直线与x轴的位置关系。
二、利用公式法

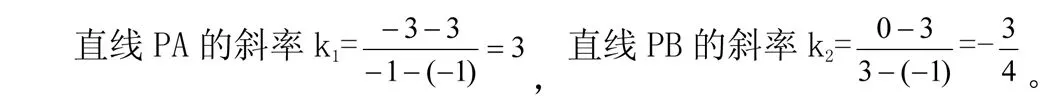

点评:直线经过的两点不分先后顺序,只要坐标保持一致即可。求斜率时要注意斜率不存在的情况。
三、利用直线方程的斜截式求斜率

四、利用向量求斜率


五、利用导数求切线的斜率
在求过曲线上一点(x0,y0)切线的斜率时,先对曲线方程求导,得到导函数,然后把x=x0带入导函数方程,得到的y,的值就是所求切线的斜率。
例7.求过曲线y=2x3+x-3上的点(2,15)的切线的斜率。
解:对y=2x3+x-3求导得:y,=6x2+1,把x=2代入上式得y,=25,
所求直线斜率为k=25。
六、待定系数法求直线斜率

点评:注意根据上面算法如果得出k不存在时,不要下结论所求直线不存在,而是此直线斜率不存在,但直线是存在的写成x=x0(x0为所过的点的横坐标)
七、利用两直线特殊关系求斜率
若两条直线平行,它们的斜率相同;若两条直线垂直,它们的斜率互为负倒数。
例9.求过点A(1,2)且与直线3x-4y+8=0①平行的直线方程,②垂直的直线方程。

九、利用“点差法”求直线斜率
在解有关以圆锥曲线某定点为中点的弦所在的直线方程的问题时,可以用“点差法”求直线斜率。

点评:利用“点差法”求直线斜率有时会产生增根,要注意检验。
[1]李小红.在中职数学中直线斜率求法的探析[J].新课程学习,2012,(10).
[2]吴茂庆.数学[M].南京:江苏教育出版社,2006.
[3]王文秀.数学复习用书[M].北京:原子能出版社,2008.

