一种基于排序的LDF改进遗传算法

An Improved Genetic Algorithm for LDF Based on Sorting

李荣雨　陈　鑫

(南京工业大学电子与信息工程学院，江苏 南京　211816)



一种基于排序的LDF改进遗传算法

An Improved Genetic Algorithm for LDF Based on Sorting

李荣雨陈鑫

(南京工业大学电子与信息工程学院，江苏 南京211816)

摘要：针对高维数据建模过程中常见的非线性复杂问题，使用遗传算法进行全局寻优。考虑到标准遗传算法在搜索过程中存在的多种收敛性问题，提出基于排序的拉普拉斯分布函数(LDF)改进遗传算法。该算法针对性地改进了遗传算法的多种收敛性问题，解决了遗传算法过快收敛至局部最优解以及后期收敛速度过慢等问题。根据实际生产数据，对轧钢精轧机组进行了仿真模拟，仿真实验结果表明了该算法切实可行，在保证了优化效果的同时，也保证了算法的总体收敛速度和稳定性，具有良好的应用前景。

关键词：高维数据算法收敛问题遗传算法拉普拉斯分布函数(LDF)适应度函数交叉算子优化算法

Abstract：In high dimensional data modeling process,the complex nonlinear problem is commonly seen,thus global optimization is conducted by using genetic algorithm.Considering the multiple convergence problems existing in standard genetic algorithm,the improved genetic algorithm for Laplace distribution function (LDF) based on sorting is proposed.The algorithm improves the multiple convergence problems,solves the problems of premature convergence of local optimum solution,and the slow convergence in late phase.The simulation based on practical productive data from the steel rolling finishing mill group is conducted,the results of simulation indicate that this algorithm is feasible,it ensures the optimization effect,overall convergence speed and stability,and possesses excellent applicable prospects.

Keywords:High dimensional dataConvergence problemGenetic algorithmLaplace distribution function (LDF)Fitness functionCrossover operatorOptimization algorithm

0引言

实际生产过程大多具有高维度、强关联和非线性等特点，一般的传统优化算法难以对其进行优化。而遗传算法因为具备智能性、并行性，并不依赖问题的内部机理，能在多数可行解中根据特定要求搜索最优解，非常适合解决复杂的非结构化、非线性、非规律性的问题[1]。但算法本身也存在一定的问题，针对这些问题，国内外学者对此进行了探索，提出了很多改进方法，大致包括：编码方式的改进[2-3]、适应度函数的改进[4]、算子的自适应改进[5-6]以及与不同分布函数的结合应用[7-8]等。本文根据前人提出的研究与改进方法，着重研究了算法收敛问题方面的改进，并在仿真实验部分测试了改进的效果，对比算法为PCCOs (parent-centric crossover operators)遗传算法[9]。实验结果表明，该算法切实可行，仿真结果达到了预期要求。

1遗传算法简介

遗传算法是一种随机性的全局优化算法，它不但具有较强的全局搜索功能和求解问题的能力，还具有简单通用、鲁棒性强、适于并行处理等特点，是一种较好的全局优化搜索算法。其核心内容按操作顺序一般分为以下5点。① 参数编码。根据问题的复杂程度或者适应度选择合适的编码，常用的编码方式有二进制编码、格雷编码、实数编码等。② 适应度函数。适应度是由目标函数变换而来，适应度的尺度变换是对目标函数域的某种映射变换，具有评价个体适应环境能力的作用，是选择操作的依据。③ 选择操作。遗传算法中的选择操作是在对个体的适应度评价的基础上，确定选取适当的个体复制到下一代中的方法，可以提高全局的收敛性，缩短整体搜索时间。常用的选择操作有轮盘赌选择法、排序选择法、联赛选择法等。④ 交叉操作。交叉操作是遗传算法中产生新个体的主要方式，也是区别于其他智能算法的重要特点，其作用是组合出新的个体，在解空间内进行有效搜索。常用的交叉算子有单点交叉、双点交叉、一致交叉、均匀交叉、算术交叉、顺序交叉和周期交叉等。⑤ 变异操作。变异是指将根据变异算子来替代个体编码中的某些基因值，以此产生一个新的个体。遗传算法中的变异运算是产生新个体的辅助方法，其目的是使遗传算法具有局部的随机搜索能力和保持群体的多样性。常用的变异算子有基本位变异、均匀变异、高斯变异等。这5部分对算法的优劣起着关键性的作用，正确的改进可以大大提升搜索到最优解的概率，并缩短搜索的时间；而不恰当的改进则会阻挠搜索到最优解的概率和效率。

2基于排序的LDF改进遗传算法

如同大多数智能算法，遗传算法具有两个较为明显的收敛性问题：一是容易出现早熟，过快收敛于局部最优解；二是后期收敛速度过慢以及收敛结果不稳定的问题。针对这些问题，本文在采用实数编码的前提下，对标准遗传算法中的适应度函数以及交叉算子两部分进行了改进。

2.1适应度函数

个体通过适应度函数可以得出其在种群中的地位，这将直接影响在下一代种群中出现的概率。传统的遗传算法中的适应度函数与目标函数呈线性关系，甚至一些简单的模型可以直接用目标函数作为适应度函数。但这种做法存在一些缺点，一是在算法的前期最大适应值与最小适应值很可能相差很大，很容易淘汰掉很多含有优秀基因片段的个体，而使得前期种群多样性遭到破坏;二是在算法后期个体间适应值的差异已经很小，使得遗传算法搜索全局最优解的能力下降。

针对这些问题，前人也提出了各种改进方法，典型的有梯度改进遗传算法[10]、基于约束区域的动态遗传算法[11]等。梯度改进遗传算法考虑了函数在搜索点的函数值及其变化率，并将该信息加入适应度函数；基于约束区域的动态遗传算法将遗传算法的全局搜索和约束区域神经网络模型的局部搜索结合起来，使用神经网络确定动态遗传算法的适应度函数。但以上算法只考虑了局部最优解问题以及整体收敛速度问题，未考虑到不同时间段算法的选择压力变化问题。针对这一问题，在两者的基础上，引入了一种基于排序的适应度函数。

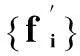
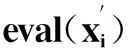
由图1～图5可知：本文设计的航向控制器使无人艇能够很好地沿着给定的航向航行，跟踪误差几乎为零。但是，仅采用动态面技术所设计的控制器，对环境扰动引起的不确定项处理效果不理想(如图5所示)。因此，引入RBF神经网络逼近器，对系统不确定项进行全局逼近处理。采用单一的在线神经网络逼近不确定项，不仅解决不确定项的逼近问题，在航向控制过程中有良好的效果，也简化了动态面控制器结构，减小计算负担。

(1)

式中：SP为选择压力，本文取2；m为种群规模。

这样改进的好处在于可以在算法前期极大地减小个体之间适应度的差异，以减小选择压力，确保前期种群的多样性，从而避免过早陷入局部最优解；同时，在算法后期相对于标准遗传算法增大了选择压力，间接加快了算法整体收敛速度。

2.2交叉算子

遗传算法中的交叉运算，是指将两个进行配对的染色体按交叉算子互相交换其部分基因，形成两个新的个体。交叉运算在遗传算法中起着关键的作用，也是遗传算法区别于其他智能算法的重要特征。常用的交叉算子有单点交叉、双点交叉、一致交叉、均匀交叉、算术交叉、顺序交叉和周期交叉等。对于交叉算子的改进，典型的有多亲遗传算法[12]、自适应杂交算子遗传算法[13]等。多亲遗传算法是一种利用了群体中心交叉方法来改进算子的遗传算法，并能将其应用到数据聚类等相关问题；自适应杂交算子遗传算法则是提出一种基于进化代数和个体适应值的交叉算子，使交叉操作向有利于算法收敛的方向进行。多亲遗传算法虽然涉及到与函数分布有关的指数型增长或是减少问题，但它的前提是必须满足一定的假设条件；而自适应杂交算子遗传算法是根据进化代数来直接修改适应度较小的个体，虽然结论表明自适应性良好，但修改后的个体有可能超出可行域。

针对以上问题，本文采用了将拉普拉斯函数与交叉算子相结合的拉普拉斯交叉算子。经改进后，该算子综合了两者的优点，既能利用函数分布特性来满足算法自适应性，同时产生的后代也仍然在其可行域内，回避了大多数情况下算子与函数结合后可行域变化的问题。

拉普拉斯的密度函数：

(2)

拉普拉斯的分布函数：

(3)

当a=0时，如b越接近0，中心附近的父代产生后代的概率较高;如b越接近1，则离中心较远处的父代产生后代的概率增大。

拉普拉斯算子交叉后的后代：

(4)

(5)

其思想来源于中间重组交叉算子和拉普拉斯分布函数。β由以下公式得出：

(6)

拉普拉斯分布函数与交叉算子结合的好处在于:可以通过改变a的取值来适应不同的具体实例，具有一定的校正作用。通过改变b的取值可以影响在解空间内搜索的整体倾向性：b值越大则搜索的结果越集中，b值越小则搜索的结果越松散。因此，需要调整适当的b值使算法在前期相对松散，以保持种群的多样性，并在后期相对集中以加快算法的收敛速度并保持收敛的稳定性。该算子也具有自适应性和一定的跳出性。根据拉普拉斯分布函数的特性，彼此接近的父代更倾向于产生彼此接近的子代，相互远离的父代更倾向于产生彼此较远的子代，产生的子代也更倾向于在父代附近，大大减少了收敛过快或者过早陷入局部最优解的情况。在陷入局部最优解的情况下，改进后的算子在不超出整体可行域的前提下具有一定的概率跳出该局部极值，重新在解空间内搜索全局最优解。为证明该算子的可行性，下文将对轧钢热连轧精轧机组进行仿真模拟。

3仿真实验

本文使用了从现场采集的数据，用基于排序的LDF改进遗传算法对热连轧精轧机组负荷分配进行优化计算。同时，为了对比其效果，本文将比较标准遗传算法、只改进交叉算子的LDF遗传算法、基于排序的LDF改进遗传算法以及PCCOs遗传算法。

精轧机组仿真模型中的目标函数为：

J=min{(P1-K1P2)2+(P2-K2P3)2+

(7)

实验钢种为Q235，来料宽度B0=1 535 mm，来料厚度H0=36.7 mm，成品厚度为5.7 mm，粗轧出口温度 TRC=10 670 ℃，精轧机组出口温度TFC=8 911 ℃,目标凸度CRn=0.016 mm，机架数n=7。实验中，算法的结构参数为：种群数大小M=500，最大遗传代数T=200，交叉概率Pc=0.9，变异概率Pm=0.01，改进交叉算子中a=0，b=0.1。

表1是各遗传算法优化负荷分配的结果，包括各机架的轧制力F1～F7以及目标函数值J。在符合轧制规程的情况下，目标函数值J越小，表明总体负荷分配就越合理。

表1各算法的轧制力负荷分配结果

Tab.1The results of the rolling force load distribution of different algorithmskN

算法名称F1F2F3F4F5F6F7J标准遗传算法235772619823816125798544964469742.3216只改进交叉算子的LDF遗传算法2180124224220221574012077945498622.0145基于排序的LDF遗传算法2219124656224151399211441857691611.6462PCCOs遗传算法20251225012045617455110911069493811.9730

图1为各算法的收敛曲线，本文采取的模型中共有7个机架。实验表明，编号越靠后的机架，收敛速度相对越慢。为使结果具有代表性，该收敛曲线是取第7个机架的变动值。

从仿真结果可以看出，图1(a)中的标准遗传算法几乎很快就陷入了局部最优解，收敛速度非常快，且不能跳出搜索到的局部最优解；而图1(b)中的只改进交叉算子的LDF遗传算法，搜索的范围明显大于标准遗传算法，并有明显的跳出局部最优解，但可以看出，其后期稳定性并不是很好；图1(c)中，改进了适应度函数，大大提高了前期种群的多样性，搜索范围再次增大，且有多次跳出局部最优解的过程，但可以看出，即使在接近收敛时，仍会有小范围的跳出最优解，只是其很快又收敛到最优解的过程，直至最后完全收敛；图1(d)采用PCCOs遗传算法，可以看出算法前期多样性很好，但却陷入局部最优解而无法跳出，收敛速度则适中。由以上分析可以看出，基于排序的LDF改进遗传算法得出的结果优于其他3种遗传算法：在符合实际生产要求的前提下，保证了算法前期的多样性，以及后期的收敛速度与稳定性，避免了出现前期陷入局部最优解以及后期收敛速度较慢等问题。

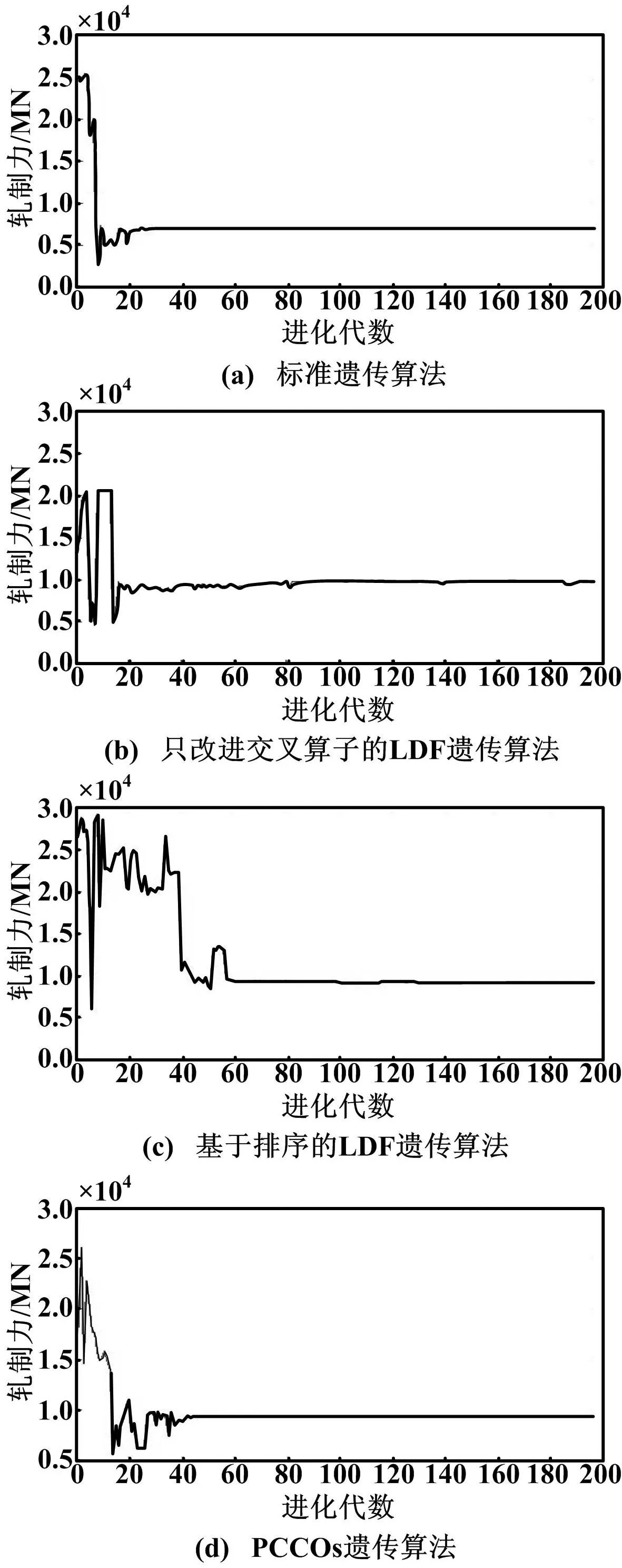
图1　各算法收敛曲线

4结束语

本文针对传统优化算法和标准遗传算法不能有效解决高维数据建模的问题，通过将适应度函数进行基于排序的自适应改进，并将拉普拉斯分布函数与交叉算子相结合，提出了基于排序的LDF改进遗传算法。

基于排序的LDF改进遗传算法针对遗传算法的多种收敛性问题，既保证了算法前期的多样性，又保证了算法后期的收敛速度与稳定性，解决了大多数遗传算法过快收敛至局部最优解，以及后期收敛速度过慢与不稳定等问题。该算法成功应用于轧钢热连轧精轧机组的负荷分配模型。通过仿真实验的对比结果可知，该算法切实可行，在遗传算法的收敛性问题方面有了很大的改善。

参考文献

[1] Holland J H.Building blocks,cohort genetic algorithms,and hyperplane-defined functions[J].Evolutionary Computation,2008,8(4):373-391.

[2] Chen Z Q,Wang R L.Two efficient real-coded genetic algorithms for real parameter optimization[J].International Journal of Innovative Computing Information and Control,2011,7(8):4871-4883.

[3] Fang N,Zhou J Z,Zhang R,et al.A hybrid of real coded genetic algorithm and artificial fish swarm algorithm for short-term optimal hydrothermal scheduling[J].International Journal of Electrical Power & Energy Systems,2014,62(11):617-629.

[4] Liu H B,Wu C L,Cheng Y C,et al.Sensor placement on bridge structure based on genetic algorithms with different fitness functions[J]. Journal of Jilin University: Engineering and Technology Edition,2012,42(1):51-56.

[5] Zhu Y G,Xu Y P,Zhou X,et al.Research on adaptive genetic algorithm injected learning mechanism[J].Computer Engineering and Application,2010,46(36):34-36.

[6] Li K,Li J H,Yang X Q,et al.An adaptive genetic algorithm based on parameters cooperated with evolution[J].Computer Simulation,2010,27(11):204-208.

[7] Deep K,Thakur M.A new crossover operator for real coded genetic algorithms[J].Applied Mathematics and Computation,2007,188(1):895-911.

[8] Deep K,Thakur M.A new mutation operator for real coded genetic algorithms[J].Applied Mathematics and Computation,2007,193(1):211-230.

[9] Garcia-Martinez C,Lozano M,Herrera F,et al.Global and local real-coded genetic algorithms based on parent-centric crossover operators[J].European Journal of Operational Research,2008,185(3):1088-1113.

[10]何新贵,梁久祯.利用目标函数梯度的遗传算法[J].软件学报,2001,12(7):981-985.

[11]陶卿,曹进德,孙德敏,等.基于约束区域神经网络的动态遗传算法[J].软件学报,2001,12(3):462-467.

[12]李平,吴佳英,郑金华,等.多亲遗传算法的理论分析及其应用研究[J].计算机工程与设计,2006,27(4):581-583.

[13]都伟,韩正之.一种自适应杂交算子的浮点遗传算法[J].系统仿真学报,2006,18(6):1711-1713.

中图分类号：TP18;TH6

文献标志码：A

DOI:10.16086/j.cnki.issn1000-0380.201602001

江苏省高校自然科学基金资助项目(编号：12KJB510007)。

修改稿收到日期：2015-05-02。

第一作者李荣雨(1977-)，男，2007年毕业于浙江大学控制系，获博士学位，副教授；主要从事工业过程的监控、优化与控制方面的研究。