基于“等效内压法”的缠绕垫片外环有限元应力分析

郑康宁，于建国

（1.保定市特种设备监督检验所，河北 保定 071000；2.承德石油高等专科学校，河北 承德 067000 ）

基于“等效内压法”的缠绕垫片外环有限元应力分析

郑康宁1，于建国2

（1.保定市特种设备监督检验所，河北 保定 071000；2.承德石油高等专科学校，河北 承德 067000 ）

对缠绕垫片外环进行了位移载荷作用下的有限元应力分析。结果表明，有限元分析结果与“等效内压法”计算的结果基本一致，从而验证“等效内压法”在外环受力分析上是适用的。

缠绕垫片；外环；有限元应力分析；等效内压法

目前，国内外对缠绕垫片的研究大多数致力于密封元件本身的研究，而对于其内外环的研究甚少。

在国标中，对缠绕式垫片的结构做出了4 种规定：（1）基本型(A 型)。（2）带外加强环型(B型)。（3）带内加强环型(C 型)。（4） 带内外加强环型(D 型)。

在美标中，对缠绕式垫片的结构型式仅做出了两种规定：（1）带外环型。（2）带外环及内环型。在美标中特别强调，所有的缠绕式垫片必需带外环(这与国标的规定不同)。

我国标准与国外标准对缠绕垫片外环上存在一定差异。此外，对内外环的作用只是定性地进行了说明，而缠绕垫片压缩后必然对内外环产生一定的作用。为了解内外环对密封元件的作用，笔者在文献[1]中首次提出了缠绕垫片外环应力分析的“等效内压法”，本文利用有限元法对缠绕垫片的外环进行了位移载荷作用下的应力分析，并验证了“等效内压法”的适用性，为缠绕垫片外环的定量研究提供了有效的方法。

1 缠绕垫片外环应力分析的前提条件

按国内外标准缠绕垫片压缩量一般为1.3mm时，在无径向约束时缠绕垫片最外圈钢带的径向位移为0.50045mm，这是认为外环和基本型装配后紧密配合得出的径向位移，而实际情况是要留有一定的余量以便外环和基本型的装配。考虑装配余量为0.8mm，即半径方向有0.4mm余量，则得到按位移全施加到外环上的位移s=0.10045mm。本文以D=550mm，外环内径317.5mm，外径外径为342.5mm,外环厚度为3mm的缠绕垫片为例进行分析（由于篇幅所限，其它尺寸外环分析略）。

2 缠绕垫片外环“等效内压法”的应力分析

根据应力分析得到外环内各点的周向应力、径向应力随半径的变化规律如图1所示。

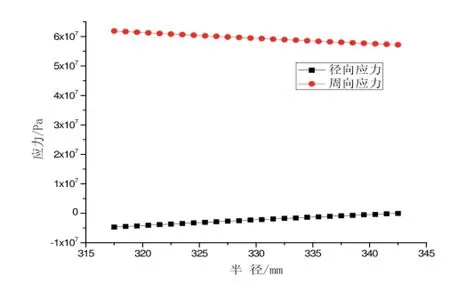
图1 “等效内压法”下的外环周向应力，径向应力分布图

周向最大应力为62.9MPa，径向应力最大值为-4.7MPa（压应力）。

3 缠绕垫片外环应力的ANSYS数值分析

3.1 建立有限元分析模型

外环的材料参数为：密度σ=7800kg/m3；弹性模量E=200GPa ；泊松比=0.3。建立实体模型。

3.2 网格划分（图2）

根据受力几何模型和对实际问题的简化，采用自由划分网格的方法（Free meshing）方法，采用四面体单元。

四面体单元在9000个左右。

图2 外环单元网格划分

3.3 加位移载荷求解

计算模型所加的载荷和边界条件见图3。模型限制Z方向的移动，在柱坐标情况下向X方向施加位移载荷。

图3 外环承载图

3.4 后处理

采用了通用后处理模块，后处理的内容包括：（1）绘制周向应力图。（2）绘制径向应力图外环数值分析结果，见图4、图5。

图4 有限元分析下的外环周向应力分布图

3.5 结果分析

将“等效内压法”与有限元应力分析所得结果绘制同一图中，见图6。

由图6可知：（1）“等效内压法”计算下的周向应力与位移载荷作用下的有限元应力分析曲线基本平行，误差很小并且误差稳定。（2）“等效内压法”计算下的径向向应力与位移载荷作用下的有限元应力分析曲线基本重合，结果基本一致。

图5 有限元分析下的外环径向应力分布图

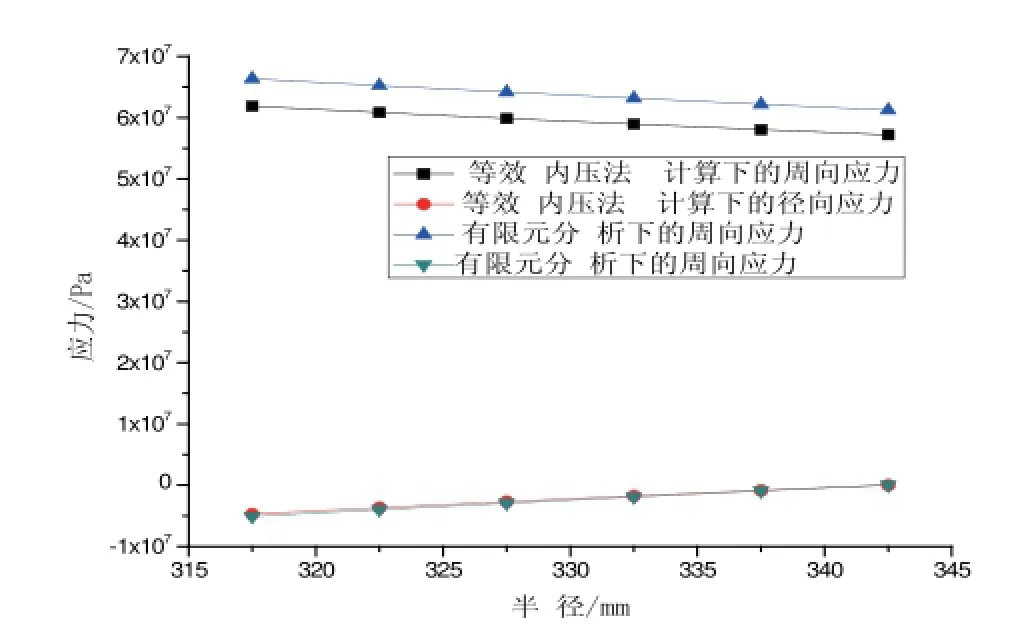
图6 “等效内压法”与有限元应力分析应力曲线对比图

4 结语

有限元分析验证表明，“等效内压法”完全适合于缠绕垫片外环在位移载荷作用情况下的应力分析，从而为缠绕垫片外环的定量研究提供了有效的方法。

[1]由立臣,郑康宁,杜利顺,等. 新型耳环式缠绕垫片的结构设计与强度计算[J].润滑与密封,2009，34(12):102～105.

[2]由立臣,陈庆,郭奇,等.缠绕垫片成型钢带压缩性能分析[J].润滑与密封,2004,(4):106～108 .

[3]陈庆,由立臣,郭奇,等.V 型缠绕垫片的力学分析及性能研究[J].润滑与密封,2002,(6):47～48.

[4]GB4622.1～4622.3-93 缠绕式垫片[S].

[5]ASME B16.20-1993 Metallic Gaskets for Pipe Flanges-Ring-Joint, Spiral-Wound, and Jacketed[S].

TB42

A

1671-0711（2016）12（上）-0101-02