基于误判率的最大差异联合分析法

陈陌，冯博文，赵威

（1.天津大学管理与经济学部,天津300072;2.中国汽车技术研究中心,天津300300）

基于误判率的最大差异联合分析法

陈陌1,2，冯博文2，赵威2

（1.天津大学管理与经济学部,天津300072;2.中国汽车技术研究中心,天津300300）

最大差异联合分析法在问卷设计和题目数量上较之其他联合分析法具有一定优势，但目前在该问卷体系下对个体判断信息的获取是一个难点，局限了方法的应用。本文充分挖掘了最大差异度量设计下的成对比较信息，通过顺序比较和三角误判率的定义，提出个人误判率的计算方法，同时利用被评价对象之间的有效对比计数和判断概率，给出了个体的最优排序法。最后通过汽车产品案例，验证了该方法的有效性。

误判率；最大差异；联合分析；个体最优排序

一、引言

联合分析法在汽车市场调研行业中有着广泛应用，很多企业在需求建议书中都会有预测产品销量或者市场占有率的诉求[1]。联合分析可以在“汽车产品”和“效用”之间建立起一种函数关系，这样消费者对某汽车产品的偏好就可以用效用值来量化，结果可以用来模拟消费者对由产品属性组合衍生出汽车产品的偏好程度，从而对市场占有率进行预测和评价[2]。

当前应用较为广泛的联合分析有以下几种：全轮廓联合分析（CVA，Conjoint Value Analysis）适用于样本量不大（小于100）的问卷形式调研；自适应联合分析（ACA，Adaptive Conjoint Analysis），适用于属性数量较多的情形，不足是需要电脑辅助，不能用笔和纸，且价格不适合当做属性，因为其输出的结果会低估价格的重要性，随着属性数量的增多，保守程度会递减[3]；以选择为基础的联合分析（CBC，Choice-Based Conjoint），它代替排序和打分形式，采用在屏幕上展示某些产品的方式，要求被访者指出哪个产品他更想购买，用彩色和立体的实物展示，模拟出了实际选择过程，让被访者就好像看到了实物一样。但不足是它并没有排序或者打分法包含更多的信息,因为尽管在每次问题中，被访者选择出了他最偏爱的产品，但并不知道他是非常喜欢还是勉强选出，同时也不知道其他没有被选产品的相对偏好[4]。最大差异联合分析（MaxDiff Conjoint，Maximum Difference Scaling Conjoint），通过最大差异度量的思想来设计问卷[5]，让被访者在每次回答中,选择出最喜欢和最不喜欢的产品，相对于当前比较流行的CBC方法，这并没有增加被访者的答题难度，但在有效信息量上却显著增加。比如在CBC方法中，被访者在一组题目中选出他最喜欢的产品,从这可以得到被访者对该产品的偏好高于同组其他产品；如果被访者同时还选出最不喜欢的产品，除了刚才所述的判断，还可以获知被访者对未被选择产品的偏好是处在最喜欢产品和最不喜欢产品之间的，有效信息成倍增加。

最大差异度量的优点在于让被访者脱离了原先纵向打分的形式，是通过横向比较判断的途径来进行信息的收集和分析[6]，机理上规避了打分方法的不足[7],但其输出结果一般是针对某一细分市场给出该市场消费者对各个属性的偏好程度及重要性排序，缺乏个体信息的判断和评价，这点对于后面进行联合分析是不利的。因此如何深入挖掘最大差异联合分析法中关于个体判断的信息，是一个很有意义的研究课题。本文在最大差异联合分析法的基础上，引入误判率的概念，通过个体综合得分，给出个体最优排序。

图1 产品属性档级示意图

二、问题描述

考虑以产品组合为背景的联合分析问题，每个产品由若干属性组成，每种属性又可分为若干个水平档级，如图1。

假设需要进行配置的属性共有M种，每种属性记为am，m∈M，每种属性am分为Lm个水平档级，一种产品的配置实际上可看作各属性都选定一个档级的排列，故最多可以组成种排列。经过正交设计后，集合包含的产品个数为v，每个产品用Si表示，记S={S1,S2,…,Sv}。再假设有n个消费者，每个人用Pi表示，记P={P1,P2,…,Pn}，经过BIBD设计，这v个产品被分在b个区组，每个区组用Bi表示，记B={B1,B2,…, Bb}，每个区组都含有k个产品，k称为区组大小；每个产品都在r个不同区组中出现，r称为处理重复数；任一对产品在λ个不同区组中相遇，λ称为相遇数。它们需要满足下面三个约束：v·r=b·k，r·（k-1）=λ·（v-1），b≥v或r≥k。

对任一个区组Bi来说，它包含k个产品，分别记为Si1,Si2,…,Sik，2≤k≤v，区组Bi中最偏爱的产品记为SiB，最不喜欢的产品记为SiW。一个区组中除了最偏爱和最不喜欢的产品，剩余产品也可以与SiB和SiW产生配对比较结果，由于同组中没有顺序误判的存在，故一共可以产生（2·k-3）对成对比较结果。

举例来说，对于一个参数为（v,k,r,b,λ）=（10,6,9,15, 5）的BIBD设计来说，每个消费者在对b=15道题做出产品选择判断之后，一共会产生（2·6-3）·15=135对成对比较的结果，而正交产品集合的个数为v=10，一共可以出现的组合数为45对。因此在135对成对比较结果中，肯定会在某些判断上出现重复，这也为误判的出现提供了空间。另外消费者关于10个产品的135对成对比较结果，也为个体的产品偏好判定提供了很好的数据基础。

三、误判率的计算

为了得到误判率的计算方式，接下来对不同产品之间的判定进行定义。由于最大差异度量的分组特点，同组中不存在相同产品自身比较和不同产品比较结果相悖的两种情形，基于此对ijk三个不同产品在成对比较时可能得出的结果排列情况进行分析。采用Qij，Qjk和Qik分别表示比较对i-j，j-k和i-k的比较结果，并将任意两个产品成对比较可能出现的结果i≻j和i≺j（表示产品Si的重要性高于产品Sj，和产品Si的重要性低于产品Sj）分别赋值Qij=1和Qij=-1。

考虑误判率的成对比较法中，可以确定评价者每种误判的次数，然后剔除掉误判率较高的评价者。但是基于误判率的最大差异度量法有所不同，以（v,k,r,b, λ）=（10,6,9,15,5）为例来说明，由于相遇数λ=5，对于一个成对比较Qij最多可以出现5次比较结果，这样就很难给出比较因素i和j的顺序误判次数。类似的，由于重复数r=9，Qij，Qjk和Qik之间的三角误判也会出现某一个判断有多个值出现的情形，这样也就对如何判定三角误判提出了更高要求。

（一）顺序误判因为同一区组内的成对比较不存在误判，即Qij+ Qji=0，记表示成对比较Q=1的个数，Q-表示ijij成对比较Qij=-1的个数。产品Si与Sj之间的判断用模糊判断Rij表示[8]，这里Rij=（1，δij）=（-1，1-δij），其中1表示i≻j表示该判断成立的概率，δij∈[0,1]；类似的显然和不能同时为零；如果同时为零，则Rij=Rji=（0,0），认为产品之间不存在判断关系。可以看到顺序误判由原先统计次数的方式转变为概率表达的模糊判断方式，这为后面三角误判的判定奠定了基础。

（二）三角误判

Parizet最早在声品质的比较中提出了关于三角误判的判断方式[9]，即通过Qij，Qjk和Qik的排列组合值来进行判定，以本文中的取值为例，每个Qij有1和-1两个值，这样三角误判一共可以有8种组合方式，见表1。Qij=1，Qjk=1和Qik=1显然是判定为正确的三角判断，Qij=1，Qjk=-1和Qik=1是判定为不定值的三角判断，Qij=1，Qjk=1和Qik=-1是判定为错误的三角判断。

本文中的顺序误判转化为用Rij来表示的模糊判断，这样在进行三角判断判定时，可以通过概率的方式来表达发生三角误判行为的发生。对一组三角判断比较，有Rij=（1，δij），Rjk=（1，δjk）和Rik=（1，δik），再定义Rijk=（1，δijk）=（0，1-δijk）为三角误判发生的概率，其中1表示发生误判，0表示正确判断和不定值，

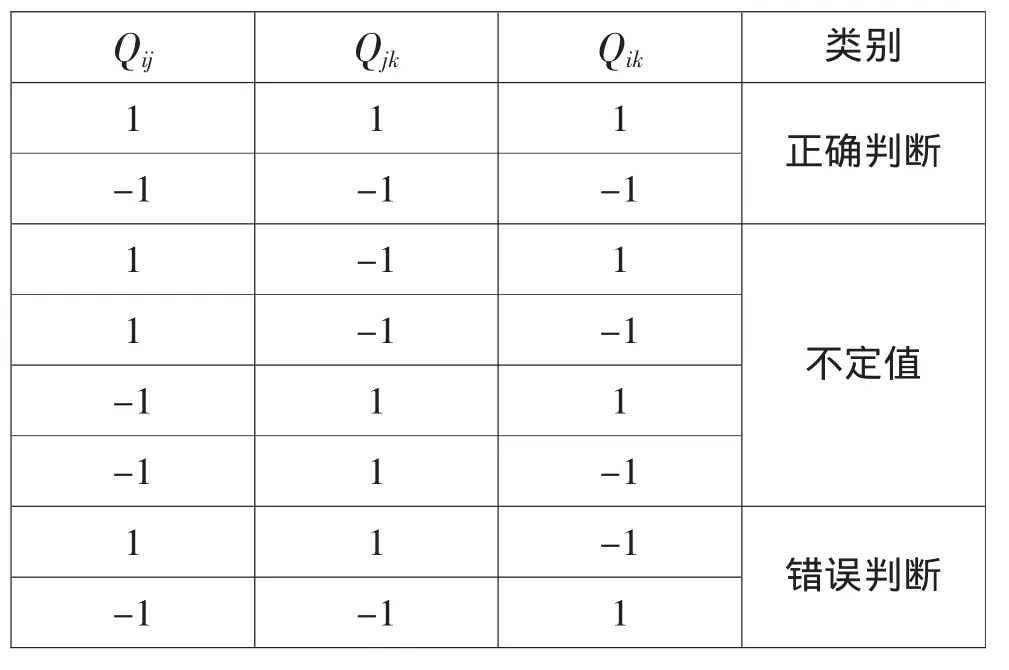
表1 三角误判判定表

四、分析方法

由前面的分析可知，在最大差异度量判断基础上，个体信息是有充分利用空间的，在顺序判断Rij=（1，δij）=（-1，1-δij）的基础上，这里给出个体最优排序的计算方法。

设评价者的个体最优排序为Oi={Si1,…,Sij，…，Siv}，其中ij∈{1,2,…,v}，Si1为重要程度排在第一位的产品，Siv为重要程度排在最后一位的产品，统计所有与产品Si1存在模糊判断关系的Sij，记Ri1,ij=（1，δi1,ij），这里令表示与产品Si1存在判断关系的计数，1≤mi1≤v-1。最后得到产品综合得分ηi1，见式（1）

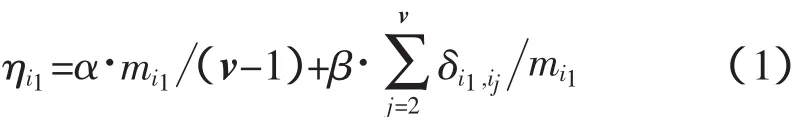
ηi1得分越高，说明产品Si1与其他产品关联越紧密，比其他产品重要的概率越高，依照ηi1得分的高低，可以对单个评价者关于被评价产品的最优排序进行衡量。

五、案例研究

（一）案例背景

某汽车企业要针对几个主要品牌中不同价格和不同配置的车辆进行市场占有率的预测。汽车产品的属性档级见表2，本次调研的有效样本为n=200。

经过正交设计后，产生了一个包含10个产品的正交产品集合，具体配置见表3。

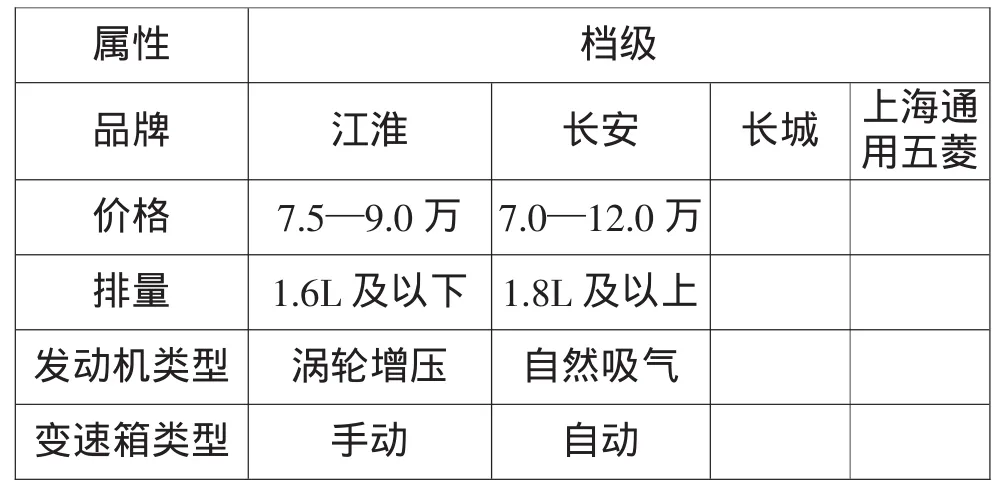
表2 汽车属性档级配置表

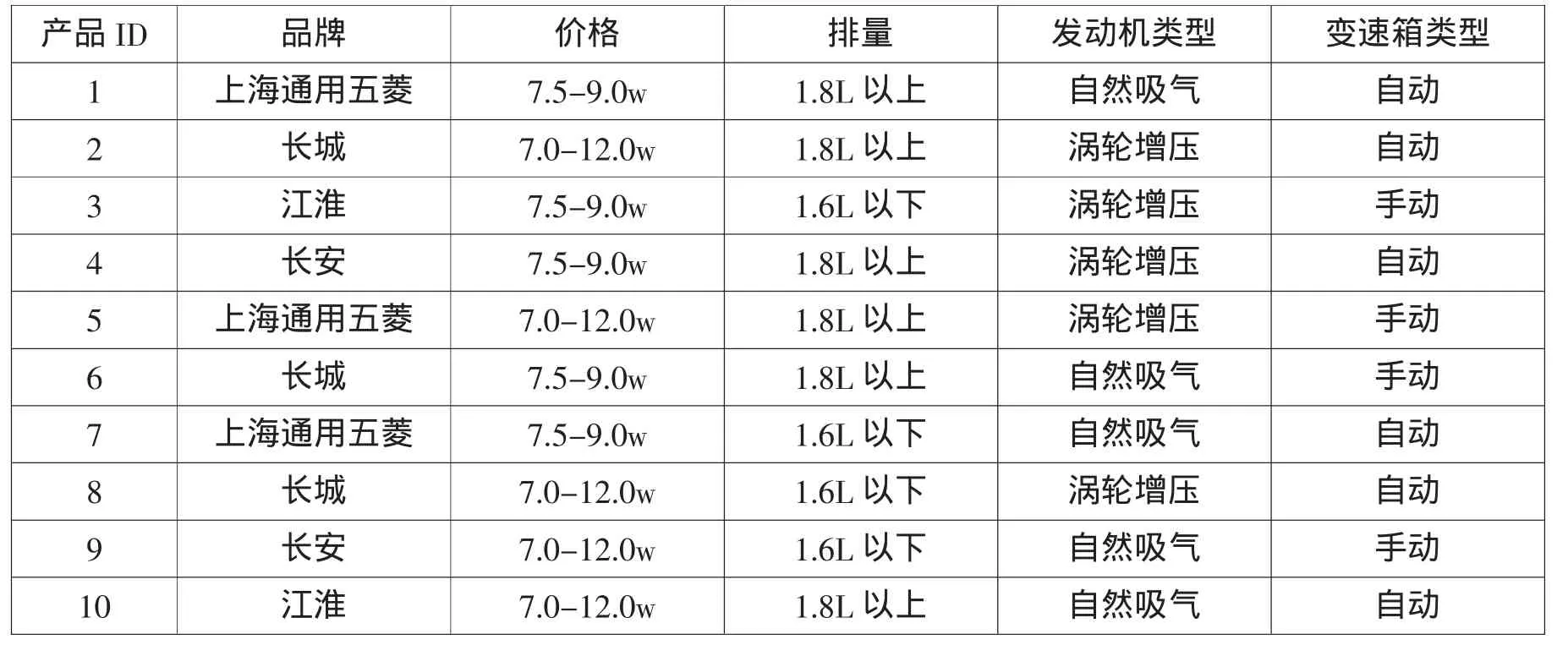
表3 正交产品配置

（二）问卷设计和误判率计算

由于v=10，因此采用（v,k,r,b,λ）=（10,6,9,15,5）的BIBD设计，问卷设计见表4。10个产品分别用1—10来标记，每个区组中均包含6个产品，每位用户在每个区组中选出最偏爱和最不喜欢的产品，然后把标记号记在相应的格子中，总共需要回答15道题。

通过顺序误判和三角误判的统计，计算出200个有效样本中每位用户的平均误判率，依照从小到大的顺序排序，遵循着排名后10—15%的评价者应予以剔除的原则，剔除了平均误判率在18%以上的评价者，共27名，见表5。对于某些评价者而言，某些顺序误判不存在，因此有效三角误判的个数是要小于的。

（三）基于误判率的最大差异联合分析

令α=0.5，β=1，利用式（1），得到每位评价者的产品综合得分ηi1，然后依据得分高低对产品排序，剔除误判率较高的评价者后，共得到173位评价者排序信息，结果见表6。

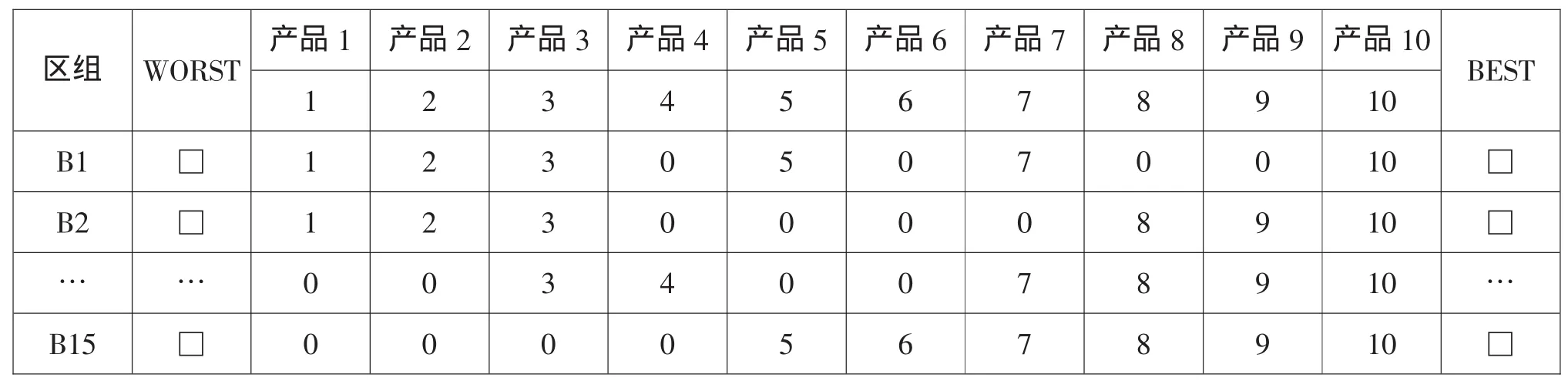
表4 BIBD问卷设计

表5 误判率较高的用户评价信息

表6 每位评价者的产品综合得分排序表

在这些信息的基础上，就可以利用联合分析来进一步对数据进行分析和处理[10]，联合分析结果见表7，可以看到变速箱类型的重要性最低，仅为10%左右，同时其效用值的绝对值也很小，可见在该细分市场，消费者并不是很看重变速箱的配备情况。品牌的重要性最高，达到了32.2%，消费者更加偏爱上海通用五菱和长城两个品牌。如果没有通过误判率获得评价者个体信息，只能通过最大差异度量得到整体市场对产品的排序，是无法得到有效可信的联合分析结果的。

六、结论

联合分析是市场调研中很重要的研究方法，sawtooth公司以此开发了很多适用于不同情形的研究模块[11]，本文对最大差异联合分析法给出了详细描述，分析了其中隐含的成对比较信息，通过误判率的定义，给出了如何判定个人排序的方法，通过汽车调研案例验证了结果的有效性，具有一定的实际应用价值。

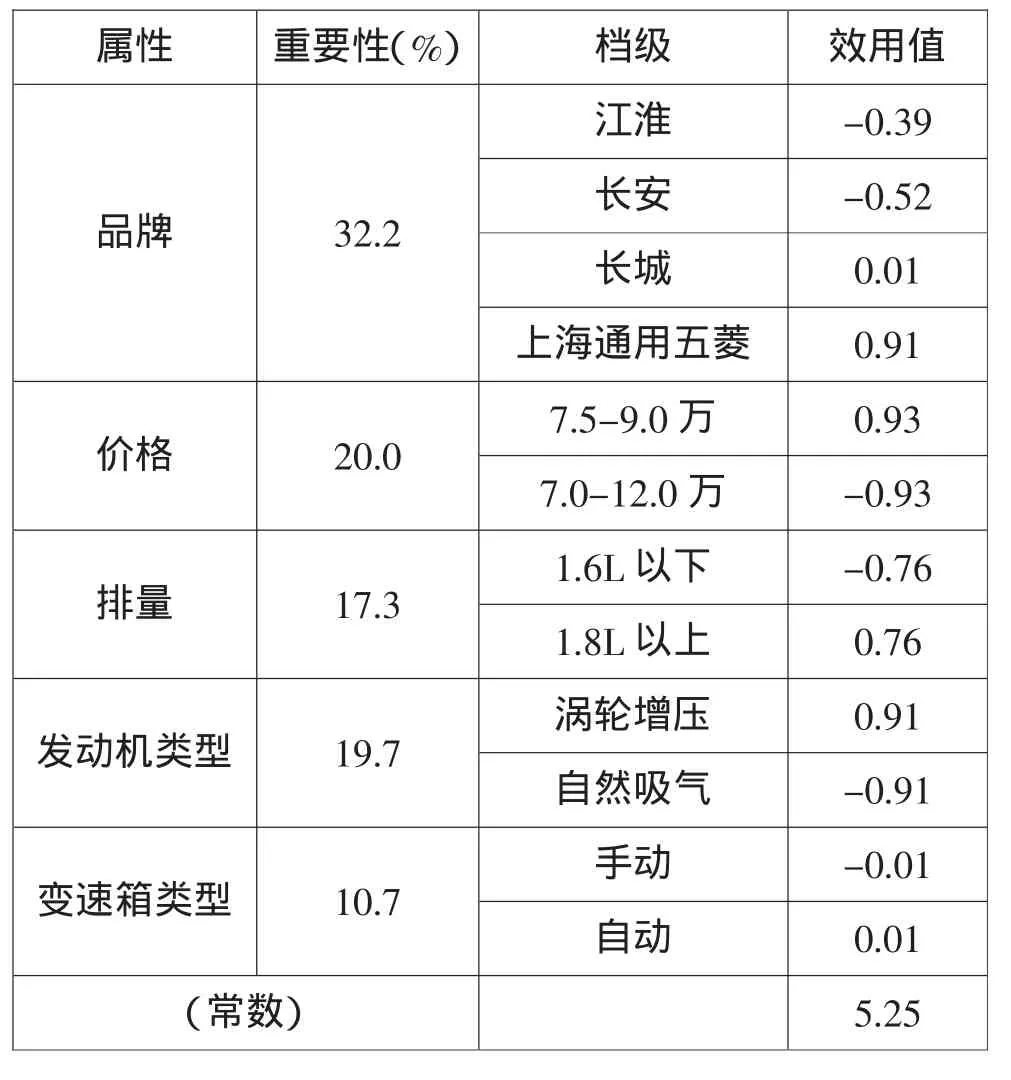
表7 属性档级效用值

[1]Green P E,Krieger A M,Wind Y.Thirty years of conjoint analysis:Reflections and prospects[J].Interfaces,2001(31).

[2]岑咏霆.联合分析方法在预测中的应用[J].工业工程与管理, 2002(7).

[3]HoppertK,MaiR,Zahn S,etal.Integrating sensory evaluation in adaptive conjoint analysis to elaborate the conflicting influence of intrinsic and extrinsic attributeson food choice[J]. Appetite,2012(59).

[4]Rao V R.Applied conjoint analysis[M].New York,NY: Springer,2014.

[5]Zhang J,Johnson F R,Mohamed A F,et al.Too many attributes:A test of the validity of combining discretechoice and best–worst scaling data[J].Journal of Choice Modelling,2015(5).

[6]Mueller S,Rungie C.Is theremore information in best-worst choice data:Using the attitude heterogeneity structure to identify consumer segments[J].International Journal ofWine Business Research,2009(21).

[7]Cohen E.Applying best-worst scaling to winemarketing[J]. International Journal ofWine Business Research,2009(21).

[8]周全.基于模糊层次分析法的高校行政服务质量评价[J].西北工业大学学报（社会科学版）,2014(4).

[9]Parizet E.Paired comparison listening tests and circular error rates[J].Acta Acustica United with Acustica,2002(88).

[10]Green Paul E,V Srinivasan.Conjoint Analysis in Marketing: New Developments with Implications for Research and Practice[J].JournalofMarketing,1990(11).

[11]Gustafsson A，Herrmann A，Huber F.Conjointmeasurement: Methods and applications[M].Berlin:Springer Science& BusinessMedia,2003.

C934

A

1009－2447（2016）04－0064－05

2016-05-05

中国汽车技术研究中心青年基金项目（16172310）

陈陌（1985-），男，天津人，天津大学管理与经济学部博士生，中国汽车技术研究中心博士后。