螺旋桨流固耦合方法及噪声预报*

杨　光　熊　鹰　黄　政

(海军工程大学舰船工程系　武汉　430033)



螺旋桨流固耦合方法及噪声预报*

杨光熊鹰黄政

(海军工程大学舰船工程系武汉430033)

摘要：采用ANSYS Mechanical有限元计算模块结合基于粘性流理论的计算流体力学方法在Workbench平台上对材料为镍铝青铜的DTMB4381桨进行双向流固耦合计算，提出顺序求解和同步求解2种方法，并与传统的计算流体力学方法对比分析，验证双向流固耦合方法的可行性和优越性.在仅考虑旋转偶极子声源的情况下，基于分离涡模型(DES)求解桨叶表面时域内脉动压力，然后采用边界元方法对某标称伴流场中的5叶大侧斜螺旋桨进行气动声学计算，预报刚性桨无空泡噪声特性.在相同工况下，以双向流固耦合方法为手段，通过傅里叶变换探究材料特性对螺旋桨噪声的影响.

关键词：螺旋桨；双向流固耦合；旋转偶极子；无空泡噪声

杨光( 1990- )：男，硕士生，主要研究领域为舰船流体动力性能

*国家自然科学基金项目资助(批准号：51179198)

0引言

复合材料由于其自身的优越性[1]，被广泛地应用到造船领域中，复合材料螺旋桨就是最主要的应用之一.由于复合材料螺旋桨独特的弯扭耦合特性，传统的理论预报(升力面、面元法)和计算流体力学方法已经不足以对其进行数值预报和深入的理论研究.国内外专家学者对复合材料螺旋桨进行了大量流固耦合研究[2-8],但以往的流固耦合方法大多采用基于势流理论的面元法，没有考虑流体的粘性；或者是通过手动迭代的稳态求解，均具有一定的局限性.

流固耦合方法是20世纪80年代兴起的一门多物理场交叉学科，涉及流体和结构的相互作用.流固耦合按数据的传递方向可分为单向和双向2种方式；按照控制方程可分为“强”“弱”2种耦合方式，“强”耦合是将流、固控制方程耦合到一个方程矩阵中求解，但这种求解方法对计算机要求十分高，在实际应用中很难实现，因此普遍采用“弱”耦合方法，即分别求解流体控制方法和固体控制方程.在Workbench中耦合可分为顺序和同步两种求解方法，顺序求解需要设定流体计算和固体计算的优先级，按顺序求解；而同步求解是同时进行流体计算和固体计算.文中分别采用流固耦合2种方法和传统的CFD计算方法对材料为镍铝青铜的DTMB4381桨进行性能预报,对结果进行对比分析验证流固耦合方法的可行性.

最后，文中基于FW-H方程采用声学边界元方法对某标称伴流场中刚性桨进行无空泡噪声预报.然后改变螺旋桨材料，通过双向流固耦合方法和傅里叶变换研究材料对噪声性能的影响.

1流固耦合计算

采用计算流体力学软件CFX和有限元软件ANSYS Mechanical在Workbench平台上通过MFX求解器进行双向流固耦合数值计算.在耦合求解步中，通过流固耦合面传递流体计算结果和固体计算结果，流体载荷使桨叶产生变形，变形后的桨叶又影响周围流场，实现流体载荷改变固体形状和固体变形改变周围流场的实时传递，直到满足残差要求计算停止.选择DTMB4381桨为研究对象，DTMB4381为5叶桨，桨模直径为0.305 m，无纵倾无侧斜.由于流固耦合计算时间较长因此只对进速系数J=0.9工况进行计算.

1.1计算模型

1.1.1流体计算模型

根据DTMB4381桨型值参数通过MATLAB编程得到各半径处桨叶剖面三维坐标点，在ICEM CFD中对螺旋桨及计算流域进行建模及网格划分，计算流域分为旋转域和静止域，为了确保桨叶网格具有周期性，文中采用结构化网格，首先对1/5旋转域创建拓扑结构，通过坍塌、点线面映射等命令划分网格，采用O-block解决桨叶周围block顶点处网格扭曲的情况，提高网格质量，为了更好地捕捉桨叶周边流场的流动情况，在桨轮廓线周围以及叶根处加密，叶根处第一层网格尺寸为桨叶直径的1/1 000，见图1.通过周期性旋转得到内域整体网格并与静止域合并，得到最终的流体计算模型，见图2.网格质量最终为0.37，网格数为2 923 076.

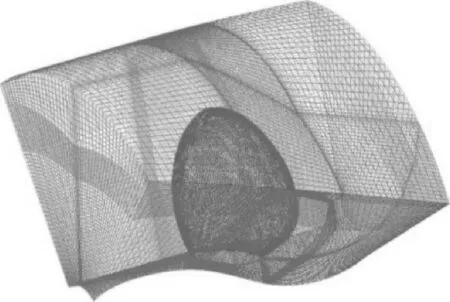
图1　1/5旋转域网格

图2　流体计算域网格

1.1.2有限元模型.

通过已有的桨叶三维坐标点在建模软件Solidworks中建立DTMB4381桨实体模型，将其导入结构计算模块中，在结构计算模块中进行实体有限元网格划分，网格数为34 792，见图3.在ANSYS mechanical中设定螺旋桨材料，材料参数见表1.将桨叶吸力面和压力面分别设为流固耦合耦合面实现流体结果和固体计算结果的实时交替，并将桨毂设置为固定约束，见图4.

图3　螺旋桨有限元模型

图4　有限元计算边界条件

材料ρ/(kg·m-3)E/GPaμNAB74001240.33

1.2流固耦合设置

流固耦合采用顺序求解方法时，流体计算和结构计算时间步长均为0.04 s，进速系数J=0.9，螺旋桨转速为600 r/min，绕x轴旋转.在流体域中设置网格变形模拟桨叶变形，速度入口为inlet，出口为outlet，相对压力设为0，远场、桨毂、桨叶均设为无滑移壁面，旋转域和静止域的交界面通过GGI连接，采用MRF技术，计算采用高阶求解模式，流体计算收敛残差为10-6，耦合收敛残差为0.01，由于是流体引起固体变形，因此优先进行流体计算.本次计算分别选取三种常见的湍流模型，k-ω,SST,k-ε进行计算，在流固耦合顺序求解中k-ε,SST极易发散，因此选择k-ε湍流模型.采用同步求解方法时，时间步长设为0.01 s，湍流模型选择SST，流体计算收敛残差设为10-4，交界面采用滑移网格技术，求解模式选择Second Order Backward Euler，其余设置与顺序求解方法相同.采用传统的CFD方法将螺旋桨视为刚性，不考虑变形，采用瞬态求解，设置与流固耦合同步求解方法中的流体计算设置相同.

1.3计算结果

表2　DTMB4381水动力性能

通过对比，3种算法水动力性能kt，10kq，ηo的最大误差分别为4.17%，1.76%，2.8%，误差满足工程应用的要求.3种计算方法的水动力性能比较相近，验证了工程中将金属桨视为刚性桨假设的合理性，出现此结果的原因是镍铝青铜合金等金属材料弹性模量较大，螺旋桨在水中运转时变形较小，螺旋桨几何的改变对周围流场的影响较小，而且DTMB4381桨无纵倾无侧斜，结构变形对水动力性能的影响不大.由于流固耦合顺序求解法比同步求解更快的达到收敛，因此在对均匀流场进行流固耦合计算时通常选择顺序求解；而在非均匀流场中通常选择同步求解，可以查看任意时刻非均匀流场对螺旋桨水动力性能的影响.

采用流固耦合算法可以直接在CFD后处理中查看结构计算结果，图5，图6分别为螺旋桨变形云图和von Mises应力分布云图.桨叶变形由叶根至叶梢沿径向逐渐增加，叶梢处的最大变形为3.245 4×10-5m，为螺旋桨直径的0.01%，同样说明了可以忽略金属桨的变形.桨叶应力由叶根至叶梢沿径向逐渐降低.

图5　螺旋桨变形云图

图6　von Mises应力分布云图

2螺旋桨噪声预报

文中基于FW-H方程，采用噪声计算软件Virtual.Lab Acoustics中的直接边界元方法对某标称伴流场中材料为铜合金的5叶大侧斜螺旋桨进行无空泡噪声数值预报，不考虑桨的变形.螺旋桨噪声源包括单极子、偶极子和四极子，四极子声源仅在接近音速的流动中作用才比较明显，而水流的马赫数较低，因此四极子可以忽略不计.单极子声源是由空泡体积的变化或者螺旋桨旋转排开一定体积的水引起，文中不考虑空泡噪声，文献[9-10]验证了厚度噪声相比于负载噪声可以忽略不计.因此文中仅考虑偶极子声源，即桨叶表面压力脉动所产生的噪声.

5叶大侧斜螺旋桨模型几何参数见表3，首先通过CFD计算得到桨叶时域内脉动压力信息，流体计算模型采用ICEM CFD创建，选择结构网格，划分方法与第一节相同，螺旋桨周围第一层网格尺寸为0.000 18，见图7，将旋转域和静止域合并得到最终计算域网格，见图8，网格数为3 921 977，网格质量为0.35以上.

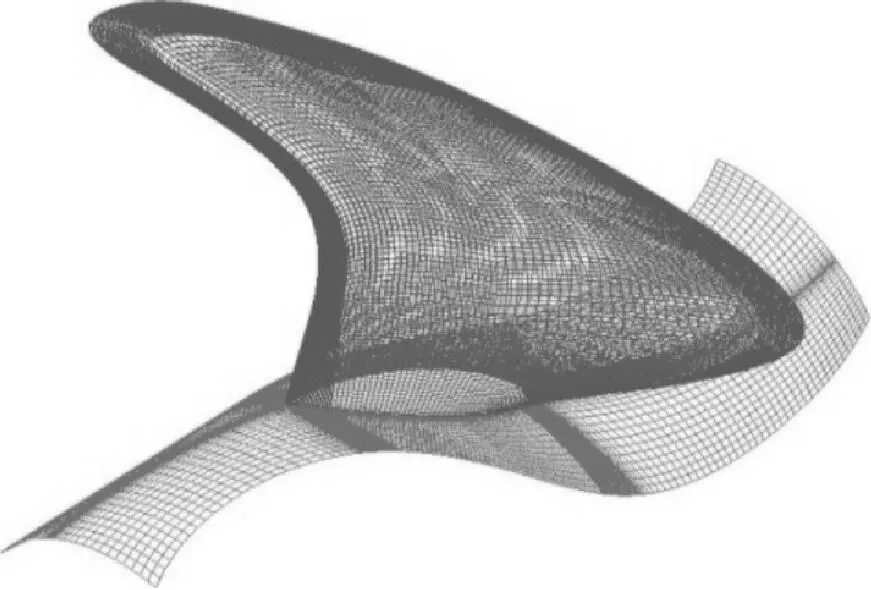
图7　桨叶、桨毂表面网格

图8　流体计算域网格

直径/m0.7R螺距比叶数盘面比毂径比0.241.35650.720.2807

首先采用定常求解螺旋桨水动力性能，转速为762 r/min，湍流模型选择k-ω，标称伴流加到速度入口，见图9，由图9可见，伴流场沿着z轴方向变化较为复杂.计算收敛后将定常结果作为瞬态计算的初值，湍流模型选择分离涡(DES)方法，时间步长Δt=0.000 5 s，即螺旋桨旋转约2.3°记录一次桨叶压力脉动信息.计算稳定后得到单桨叶和5个桨叶上在2个旋转周期内时域轴向脉动压力曲线，见图10、图11.

图9　非均匀伴流场云图

图10　单桨叶轴向脉动压力

图11　桨叶轴向脉动压力

图12　声学网格

图13　声场

通过计算，得到各监测点的噪声频谱特性，图14为x轴方向噪声频谱曲线.各监测点的总声压级根据式(1)计算，见表4.

(1)

图14　x轴监测点频谱曲线

监测点x1x2y1y2z1z2SPL/dB156.47145.59123.76100.01100.1101.29

从各监测点的总声压级可知，轴向噪声对总噪声贡献量最大.分别对5个桨叶时域内轴向脉动压力进行傅里叶变换转换为频域内脉动信息，得到图15，由图可知，轴向脉动压力在叶频和倍叶频附近出现幅值，与螺旋桨轴向监测点噪声频谱曲线规律一致，而且一阶叶频处脉动压力对总噪声级的影响最大.接下来改变螺旋桨材料，采用双向流固耦合方法对弹性桨进行数值计算，研究材料特性对螺旋桨噪声的影响.

图15　螺旋桨频域内轴向脉动压力

螺旋桨材料改为各向异性的碳纤维复合材料，材料特性见表5，不考虑复合材料的铺层结构，工况保持不变，水动力计算模型采用刚性桨模型，有限元计算模型见图16，首先采用顺序求解法进行双向流固耦合计算，湍流模型选择k-ω，待计算收敛，将其作为初值进行瞬态双向流固耦合计算，湍流模型选择SST，考虑计算时间的问题，时间步长Δt=0.001 s，计算稳定后，得到螺旋桨变形分布，见图17，由叶根至叶梢沿着径向变形逐渐增大，桨叶最大变形为螺旋桨直径的0.164%，是第一节中镍铝青铜螺旋桨的10倍，因此对复合材料螺旋桨进行水动力性能计算时，要考虑螺旋桨的弯扭耦合特性.

表5　材料参数

图16　有限元模型

图17　螺旋桨变形云图

复合材料螺旋桨桨叶表面轴向脉动压力见图18.通过傅里叶变换得到复合材料螺旋桨频域内轴向脉动压力，见图19，由图可知在叶频附近脉动出现幅值，而且在叶频和倍叶频附近脉动幅值较金属桨降低很多，侧面反映出复合材料噪声性能要优于刚性桨，具有减振降噪的优点.图20分别为金属桨和复合材料螺旋桨盘面处轴向速度分布云图，从图中可知在伴流场变化较为复杂区域(z轴方向)，复合材料螺旋桨叶梢流场的变化较金属桨更为平缓，这是由于复合材料螺旋桨的变形对来流具有自适应性的原因.

图18　复合材料螺旋桨轴向脉动压力

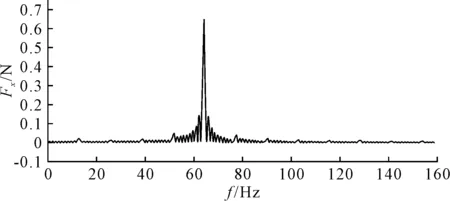
图19　复合材料螺旋桨频域内轴向脉动压力

图20　螺旋桨盘面处轴向速度分布

3结 束 语

文中采用顺序和同步两种双向流固耦合计算方法对材料为镍铝青铜的DTMB4381桨进行性能预报，在Workbench平台上实现计算流体力学结果和有限元计算结果的实时传递.与试验值对比，验证流固耦合方法的准确性.然后采用声学直接边界元方法预报了某标称伴流场中镍铝青铜合金五叶大侧斜螺旋桨无空泡负载噪声特性，说明了轴向脉动压力和负载噪声的关系.并在相同工况下，将此桨材料改为碳纤维复合材料，对其进行瞬态双向流固耦合计算，得到复合材料螺旋桨的水动力性能和结构特性.通过对比两个桨频域内脉动压力特性，侧面说明碳纤维复合材料螺旋桨具有减振降噪的优点.

参 考 文 献

[1]张帅，朱锡，孙海涛，等.船用复合材料螺旋桨研究进展[J].力学进展，2012,42(5):620-633.

[2]YOUNG Y L. Time-dependent hydroelastic analysis of cavitating propulsors[J]. Journal of Fluids & Structures, 2007,23(2):269-295.

[3]YOUNG Y L. Fluid-structure interaction analysis of flexible composite marine propellers[J]. Journal of Fluids & Structures, 2008,24(6):799-818.

[4]YOUNG Y L. Fluid-structure interaction analysis of flexible composite marine propellers[J]. Journal of Fluids & Structures, 2008,24(6):799-818.

[5]LIU Z, YIN L Y. Utilization of bend-twist coupling for performance enhancement of composite marine propellers[J]. Journal of Fluids & Structures, 2009,25(6):1102-1116.

[6]LIN C C, LEE Y J. Stacking sequence optimization of laminated composite structures using genetic algorithm with local improvement[J]. Composite Structures, 2004,63(3-4):339-345.

[7]孙海涛,熊鹰.考虑变形的螺旋桨水动力及变形特性研究[J].哈尔滨工程大学学报,2013,34(9):1108-1112.

[8]张帅,朱锡,侯海量.船舶螺旋桨流固耦合稳态求解算法[J].哈尔滨工程大学学报,2012,33(5):615-621..

[9]SEOL Hanshin,SUH Jung-Chun,LEE Soogab.Development of hybrid method for the prediction of underwater propeller noise[J]. Journal of Sound and Svibration, 2005,288(1-2):345-360.

[10]苏玉民,窦凤祥,刘业宝,等.螺旋桨无空泡噪声的研究[J].武汉理工大学学报：交通科学与工程版,2013,37(5):895-899.

Fluid-structure Coupling and Numerical

Noise Prediction of Propeller

YANG GuangXIONG YingHUANG Zheng

(DepartmentofNavalEngineering,NavalUniversityofEngineering,Wuhan430033,China)

Abstract：In the commercial software ANSYS Workbench, the paper combines FEM solver ANSYS Mechanical with CFD solver based on viscous fluid theory to accomplish synchronously or sequentially two-way fluid-structure coupling of NAB DTMB4381, then compares the results from FSI method and from traditional CFD method with experimental result to confirm the validity and advancement of coupled FSI. In some non-uniform flow field ,the fluctuating pressure on blades in time domain was simulated by choosing DES as turbulence model, then non-cavitation noise of highly skewed propeller was predicted by the method of BEM only considering acoustic rotating dipole .In the same working condition, two-way FSI and FFT is used to explore the influence of blade material on propeller noise.

Key words：propeller; two-way fluid-structure coupling; acoustic rotating dipole; non-cavitation noise

收稿日期：2015-11-05

doi:10.3963/j.issn.2095-3844.2016.01.030

中图法分类号：U664.33