基于动态执行机构的欠驱船舶循迹控制*

徐海祥　瞿　洋　余文曌　殷进军　龙　飞

(高性能船舶技术教育部重点实验室1)　武汉　430063)　(武汉理工大学交通学院2)　武汉　430063)

(武汉船用电力推进装置研究所3)　武汉　430063)



基于动态执行机构的欠驱船舶循迹控制*

徐海祥1，2)瞿洋2)余文曌1，2)殷进军3)龙飞3)

(高性能船舶技术教育部重点实验室1)武汉430063)(武汉理工大学交通学院2)武汉430063)

(武汉船用电力推进装置研究所3)武汉430063)

摘要：欠驱船舶的循迹控制已成为国内外动力定位研究的难点.针对船舶循迹控制中横向偏差最小问题，文中利用line-of-sight (LOS) 引导律将船舶期望位置转化为期望首向；为了满足动态执行机构的饱和、死区和迟滞等物理限制，将执行机构的动态响应方程并入到三自由度操纵数学模型中，使控制输出更加平滑；针对欠驱船舶横向控制力无法满足的问题，设计了一种基于Lyapunov理论的两输入反步积分控制器.数值仿真验证了执行机构的动态响应方程和反步积分控制器的有效性.

关键词：动态执行机构；循迹控制；LOS引导律；反步积分

徐海祥(1975- )：男，博士，教授，博士生导师，主要研究领域为海洋动力定位系统开发

*国家自然科学基金资助(批准号：61301279)

0引言

船舶循迹控制是指船舶在作业或航行过程中，沿某一条预定轨迹以恒定的纵向速度前进，在此过程中必须保持船舶的首向沿着预定轨迹.船舶循迹控制的控制目标主要包括航迹的保持和纵向速度的控制[1].在循迹控制过程中，船舶所需的首向角由引导系统产生.

欠驱船舶循迹控制是船舶循迹控制的一个难点.欠驱船舶是指船舶的执行机构的配置无法同时满足纵向、横向和首向的控制要求.对于欠驱船舶而言，其配置形式一般是主推与舵，主推用于产生船舶前进所需的速度，而舵主要产生转首力矩.欠驱船舶的最低配置是一个主推和单舵的组合，其执行机构往往只有主推和舵机，船舶的横向控制力是无法满足的.早期，欠驱船舶的循迹控制问题常用到的是野本谦作(Nomoto)操纵数学模型，但其缺点是不能将环境扰动力里考虑到模型当中[2].20世纪90年代后期，三自由度的船舶操纵数学模型在欠驱船舶控制中得到了应用，其可以考虑船舶纵向和首摇方向的环境扰动力影响，但无法考虑到横向扰动力的影响[3-4].随后，国内外欠驱船舶循迹控制的研究重点转为如何抵抗环境扰动力，特别是流的影响[5-7].

由于假设执行机构能够迅速满足控制输出，因而执行机构的动态响应往往被忽略.但实际的执行机构存在饱和、死区和迟滞等物理限制，因此执行机构的动态响应不能够被忽略.对于动态执行机构问题，大多数的做法是将其考虑到推力分配的静态分配当中，但这种做法无法从根本上解决高频控制输出的问题[8]；较好的做法是将其考虑到操纵数学模型中，使控制器的设计不仅能够能满足整个系统的稳定而且控制输出相对平滑[9].一般，执行机构的动态响应方程可视为具有低通滤波功能的一阶惯性环节.

针对欠驱船舶循迹控制问题，以上文献大都侧重于如何抵抗外部环境扰动力而忽略了执行机构动态响应问题.在以上文献的基础上，本文利用LOS引导律将船舶期望位置转化为期望首向，在三自由度操纵数学模型中考虑动态执行机构方程，利用Lyapunov理论设计了一种不考虑横向控制力的反步积分控制器，实现了对未建模环境力的补偿.

1引导律的设计

对于船舶循迹控制来说，引导律的设计是在一个二维平面坐标系内完成的.首先引入路径平行坐标系(path parallel)的概念，该坐标系的X轴与路径相切，Y轴与X轴垂直形成右手坐标系，见图1.相较于更加复杂的一般曲线引导系统的设计，这里将介绍基于直线和圆弧的引导系统的设计.图中Pp点为路径平行坐标系的原点；P点为船体坐标系原点.

对于直线路径来说，船舶此时所需要的首向ψd即为图中所示的引导首向角χs，χs可表示为

(1)

图1　直线和圆弧的LOS引导律

对于圆弧路径来说，船舶此时所需要的首向ψd即为图中所示的引导首向角χc，χc可表示为

(2)

为了减小循迹控制过程中的振荡，时变的前向距离Δ可取为[10]

(3)

式中：ρ为前向距离Δ的收敛速率.当偏差越大时，Δ越小，以此获得较快的转首，反之Δ越大，以此减小较小Δ引起的振动.

2船舶数学模型

考虑到执行机构的动态响应方程，三自由度船舶操纵数学模型为

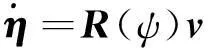
(4)

(6)

式中：η=[x,y,ψ]T为船体在固定坐标系下的位置；v=[u,υ,r]T为船体在运动坐标系下的速度；R(ψ)∈R3×3为坐标系旋转矩阵；MRB∈R3×3为刚体惯性矩阵；MA∈R3×3为附黏水惯性矩阵；D∈R3×3是阻力的线性部分；Bu为船舶执行机构的配置矩阵；up=[Tp,δ]T为螺旋桨推力Tp和操舵角δ组成的向量；τw为风载荷，主要依据风载荷系数，风向βw和风速Vw计算；b∈R3×1是作用于船体上的未建模环境扰动力，包括风浪流的未建模扰动力；Tu为表征执行机构动态响应速率的定常矩阵；uc=[Tpc,δc]T为控制器的输出；vr是船体在运动坐标系下相对于流速vc的相对速度.vr和v的关系可以表示成如下形式.

(7)

式中：Vc和βc分别为流速的大小和流向角.考虑到执行机构的饱和问题，控制器的输出需要作如下限制.

(8)

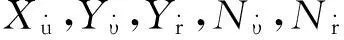
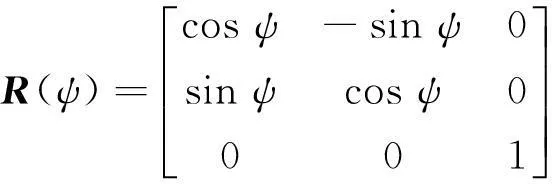
3反步积分控制器设计

在文献[11]的研究基础上，本文根据线性操纵运动模型进行自适应未建模环境力的反步积分控制器设计.

定义有如下的投影向量和偏差向量.

(9)

式中：α1=[α11,α12,α13]T∈R3为虚拟控制项.

第一步，第一个Lyapunov函数定义为

(10)

对上式求导：

(11)

将式代入上式得

(12)

因此，虚拟控制量α13可以选为

(13)

式中，c1>0，式(12)可以化简为

(14)

第二步，定义第二个Lyapunov函数：

(15)

对式(15)求导：

根据线性操纵运动数学模型

(17)

式中：Buup可作为第二个虚拟控制量.因此，式(16)可以写为

(18)

因此，虚拟控制量α2可取为：

rMASTR(ψ)Tvc-DR(ψ)Tvc-K2z2

(19)

式中：K2为正定的对角矩阵，取如下的自适应的未建模环境力：

(20)

定义第三个偏差向量：

(21)

第三步，第三个Lyapunov函数定义为：

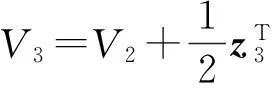
(22)

对式(22)求导，并带入式(6)、(18)和(19)得：

(23)

对于欠驱动船舶，其三个方向的控制力为τ=Buup.为了满足转首力矩τ3，横向控制力就无法满足，通常可以假定横向控制力为零，即τ2=0.对于实际的船舶，其转首力矩通常由操舵产生，同时也会产生相应的横向力，即τ2=ετ3，参数ε=Yδ/Nδ不为零，控制力的形式可以表示为

(24)

针对欠驱船舶推力和操舵角存在动态限制的问题，可将配置矩阵Bu进行降维处理.

(25)

结合式和式，为了使系统稳定，纵向和首向的控制率可以设计为

(26)

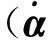
(27)

在循迹控制过程中，希望船舶沿某一条预定轨迹以恒定的纵向速度ud前进，在此过程中必须保持船舶的首向沿着预定轨迹.因此，虚拟控制项α1可以写成如下形式.

(28)

4实验仿真

本文仿真中用到的船模是挪威科技大学的Cybership 2，模型、LOS引导律、控制器和环境力等参数的设定值见表1.设定的4个轨迹点坐标及相应的圆弧半径为：P1=(0,0),P2=(5,20),P3=(20,15),P4=(30,30),Ri=(3,3).

针对循迹控制对位置保持和速度控制的要求，结合所设计的自适应未建模环境力反步积分控制器，文中给出了相关的仿真结果图.图2显示了循迹控制中的反步积分控制器具有非常好的效果，船舶的横向偏差在很短时间内迅速减小.图3说明在仿真开始后的前面若干个周期内，时变的前向距离Δ能使船舶迅速转首到所需的首向角，随后的控制首向也与所需的船舶首向吻合得非常好.图4给出了船舶循迹过程中的横向偏差，仿真结果说明船舶稳定状态下的横向偏差均在0.1 m以下.图5显示了船舶的纵向速度控制得非常好，保持在0.1 m/s左右，横向速度在最后也慢慢趋近于零.这从侧面也证明了即使横向控制无法满足，只要时间足够长，横向速度会慢慢趋近于零.图6说明了自适应未建模环境力慢慢地趋近于设定的未建模环境力，反应了未建模环境力自适应律的有效性.图7显示了欠驱船舶在只满足纵向推力和转首力矩条件下的控制输出uc，由于设计控制器时将控制量设为螺旋桨推力和操舵角，因此可以更为直接地将螺旋桨推力和操舵角的输出限制考虑进来，尽量避免出现无法分配所需控制力的情况.另外，在控制器设计过程中还考虑了执行机构的动态响应过程，将控制量设为uc而非实际输出up，这样便能够让控制信号更好地满足船舶的实际响应需求.

表1　相关参数设定值

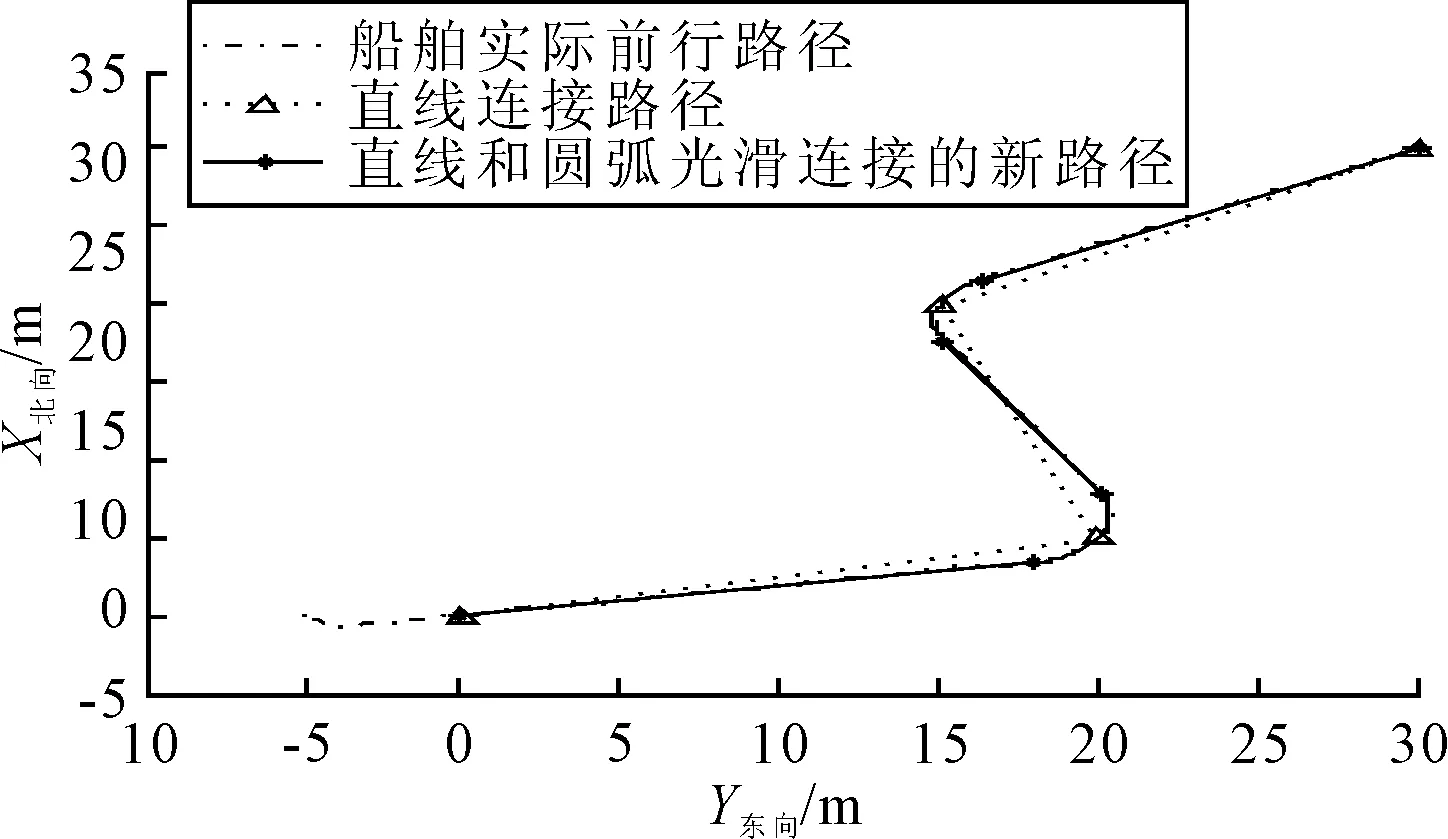
图2　船舶运动轨迹图

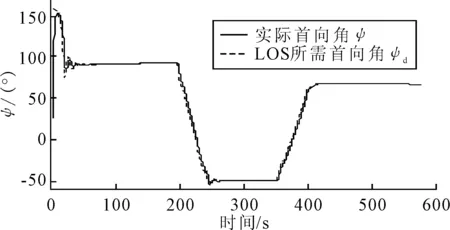
图3　船舶实际首向角和所需首向角

图4　船舶横向偏差

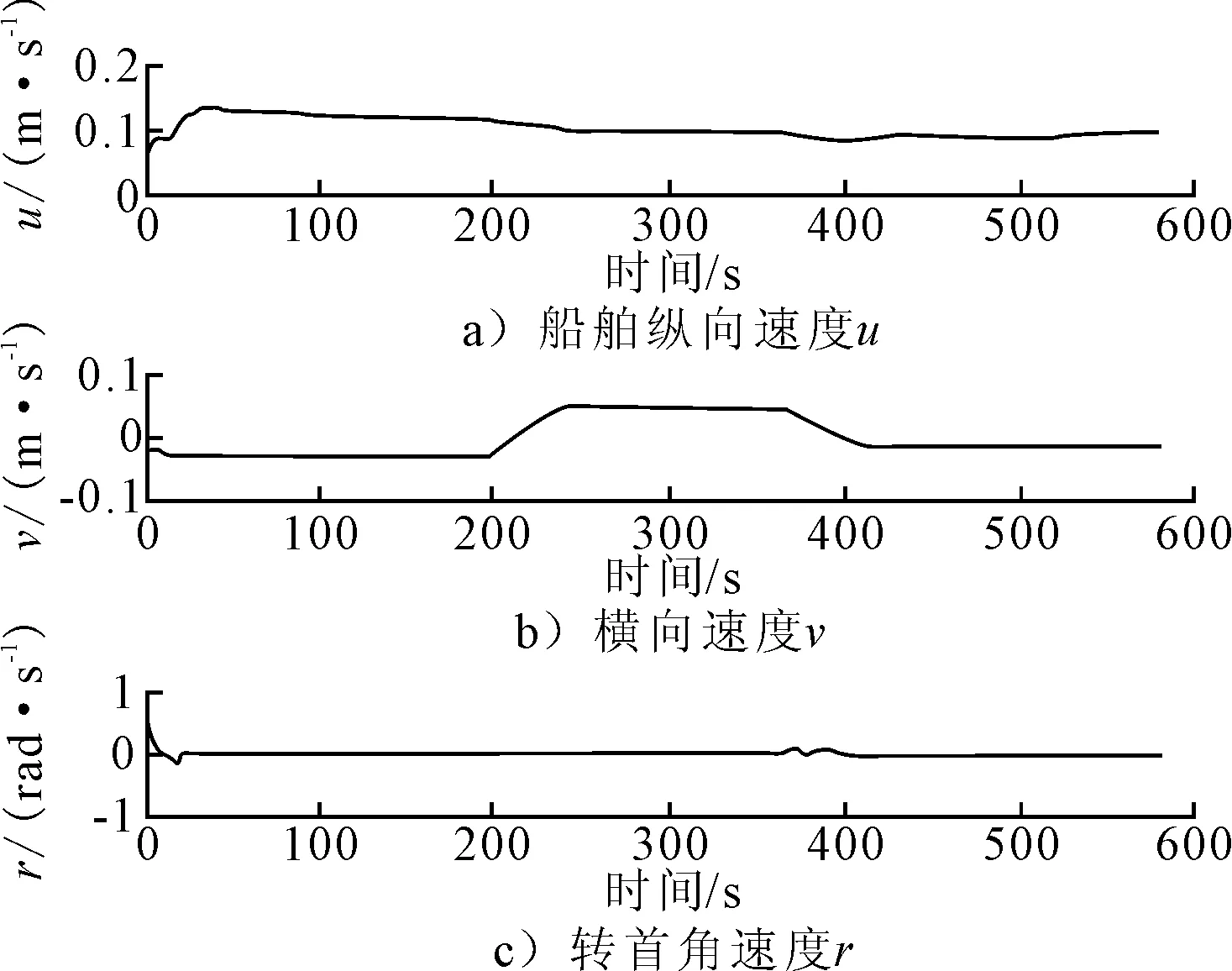
图5　船舶运动的速度

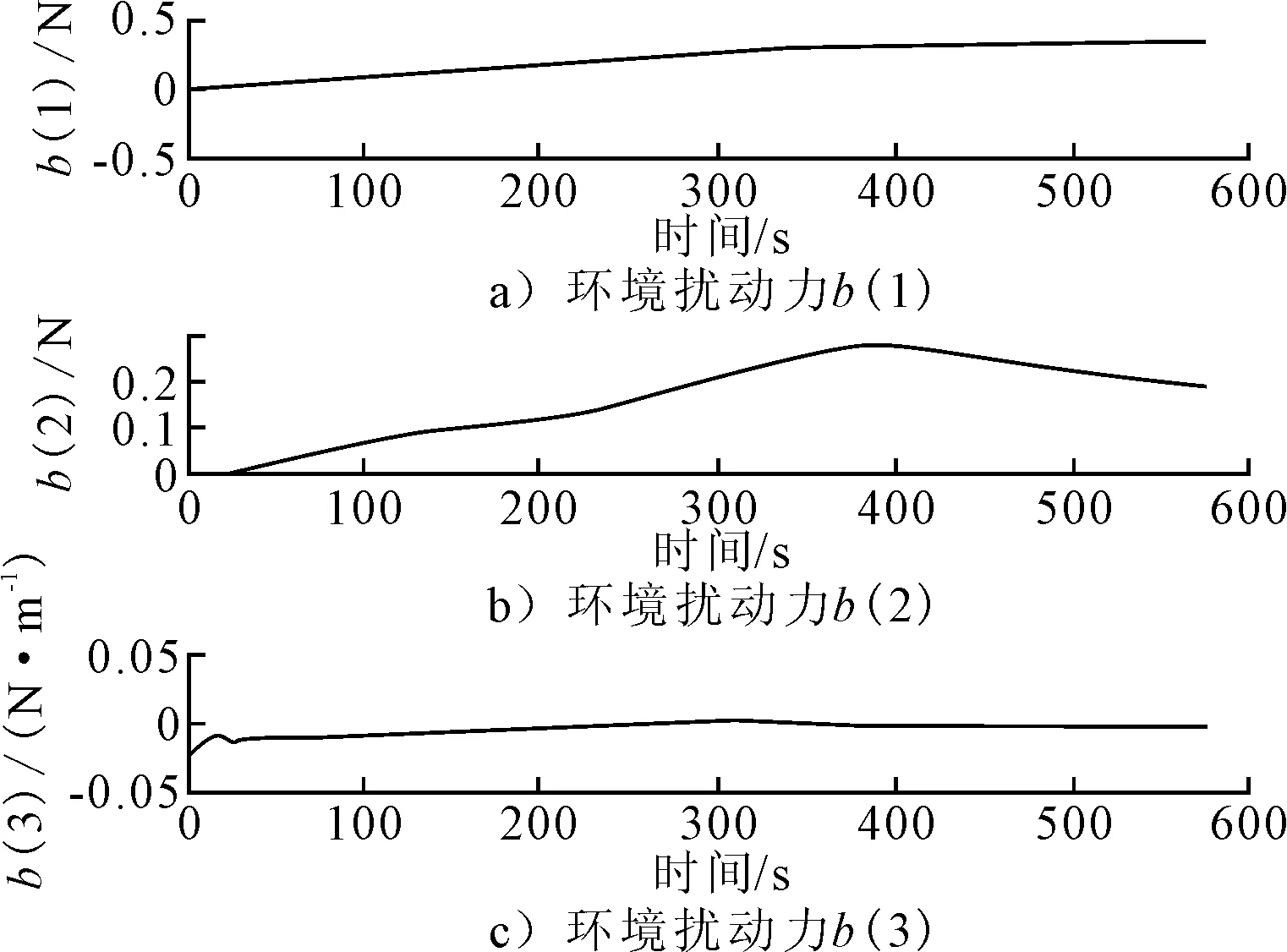
图6　自适应未建模环境力

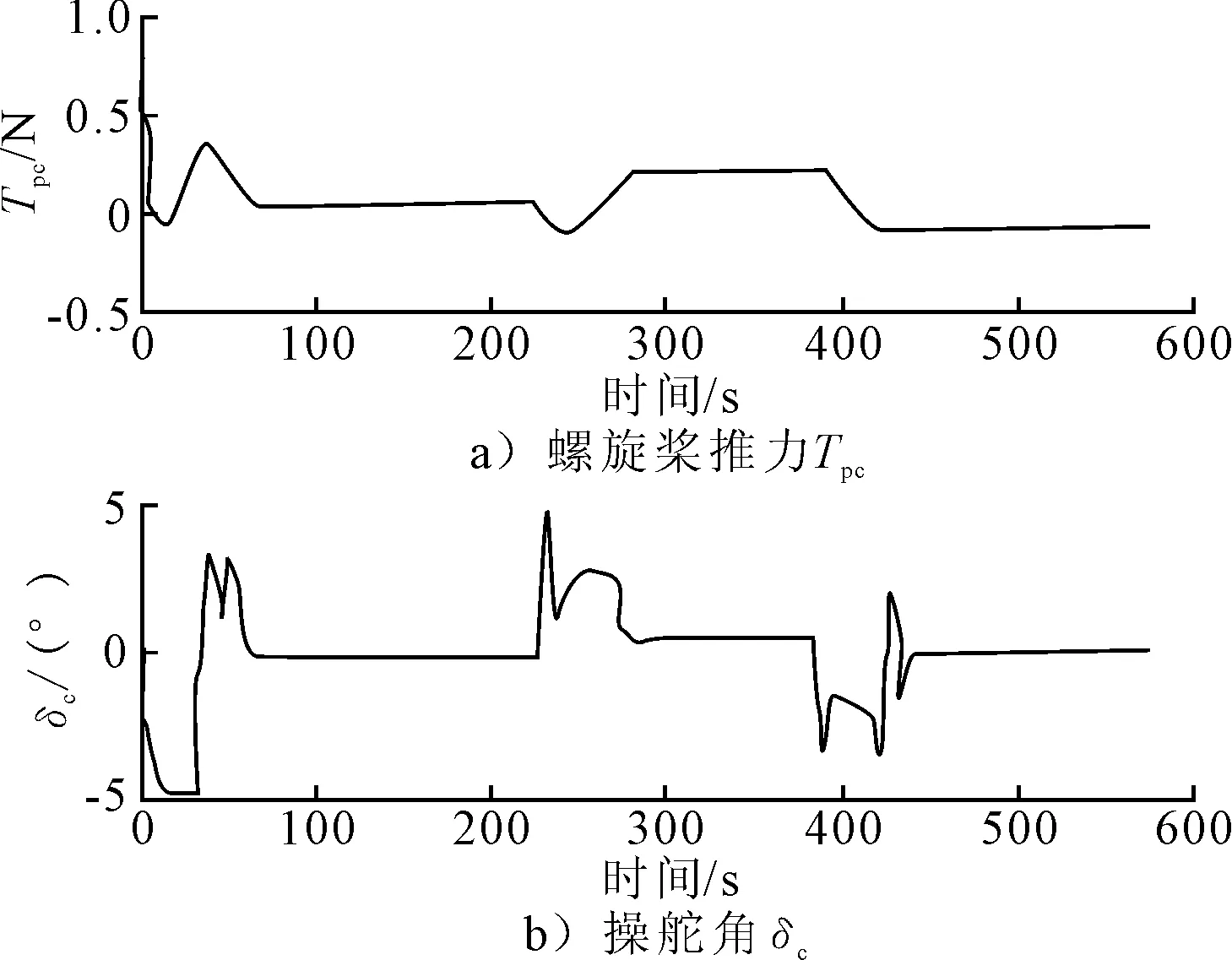
图7　船舶控制输出uc

5结 束 语

针对欠驱动船舶循迹控制中的航迹保持问题，本文利用了LOS引导律来获得船舶所需的首向角，同时使循迹控制过程中的横向偏差最小.针对动态执行机构存在物理限制和欠驱船舶横向控制力无法满足的问题，本文将执行机构动态响应方程并入到三自由度操纵模型中，设计了不考虑横向控制力的两输入反步积分控制器，实现了对未建模环境力的在线自适应补偿，达到了对船舶首向和前进速度平稳控制的目的.

参 考 文 献

[1]SKJETNE R, FOSSEN T I， KOKOTOVIC P. Output maneuvering for a class of nonlinear systems[C]. Proceedings of the 15th IFAC World Congress on Automatic Control, Barcelona, Spain,2002.

[2]FOSSEN T I. Guidance and gontrol of ocean vehicles[M]. Hoboken： John Wiley & Sons,1994.

[3]SIRA R H. On the control of the underactuated ship: A trajectory planning approach[C]. Proceedings of the 38th IEEE Conference on Decision and Control,1999(3):2192-2197.

[4]PETTERSEN K Y, FOSSEN T I. Underactuated dynamic positioning of a ship-experimental results[J]. IEEE Transactions on Control Systems Technology,2000,8(5):856-863.

[5]MENG W, GUO C, CHEN R. Adaptive output feedback control for path following of underactuated ships with uncertain dynamics[C]. Proceedings of the 27th Conference on Control and Decision,2015:5383-5386.

[6]CAHARIJA W. Integral line-of-sight guidance and control of underactuated marine vehicles[D]. Norwegian： Norwegian University of Science and Technology,2014.

[7]LEKKAS A M. Guidance and path-planing system for autonomous vehicles[D]. Norwegian：Norwegian University of Science and Technology,2014.

[8]BERGE S P, FOSSEN T I. Robust control allocation of overactuated ships; experiments with a model ship[C]. Proceedings of the 4th IFAC Conference on Manoeuvring and Control of Marine Craft，1997:166-171.

[9]MORISHITA H M， SOUZA C E S. Modified observer backstepping controller for a dynamic positioning system[J]. Control Engineering Practice,2014,33:105-114.

[10]LEKKAS A M, FOSSEN T I. A time-varying lookahead distance guidance law for path following[C]. Proceedings of 9th IFAC Conference on Manoeuvring and Control of Marine Craft, Arenzano, Italy,2012.

[11]FOSSEN T I, BREIVIK M， SKJETNE R. Line-of-sight path following of underactuated marine craft[C]. Proceedings of the 6th IFAC MCMC, Girona, Spain,2003:244-249.

Path Following for Underactuated Marine

Craft with Actuator Dynamics

XU Haixiang1，2)QU Yang2)YU Wenzhao1，2)YIN Jinjun3)LONG Fei3)

(KeyLaboratoryofHighPerformanceShipTechnology

ofMinistryofEducation,Wuhan430063，China)1)

(SchoolofTransportation,WuhanUniversityofTechnology,Wuhan430063，China)2)

(WuhanInstituteofMarineElectricPropulsion,Wuhan430063，China)3)

Abstract：Recently, path following for underactuated marine craft has become a difficult problem. To minimize the cross-track error to the path, a line-of-sight (LOS) guidance law is introduced to reduce the control outputs from the desired position to the desired heading angle. In order to satisfy the saturations, dead-zones and hysteresis of the actuators, the actuator dynamics equation is added into the 3DOF maneuvering model to obtain a smooth control outputs. Considering that the sway force of the underactuated ship could not be satisfied, a backstepping controller with two outputs has been designed based on Lyapunov theory. In addition, the validity of the actuator dynamics equation and the backstepping controller is demonstrated by the simulation using the maneuvering model.

Key words：actuator dynamics; path following; line-of-sight guidance; backstepping

收稿日期：2015-10-09

doi:10.3963/j.issn.2095-3844.2016.01.002

中图法分类号：U675.91