“几何直观”在小学数学教学中的运用

黄艳

《义务教育数学课程标准》指出：“几何直观主要是指利用图形描述和分析问题.”数学教师进行授课过程中，由于小学生自身特点决定，其思维模式单一，具有一定的局限性，且知识储备有限，因此，教学环节往往会出现某些困难或障碍.几何直观具有形象性强的特性，能帮助学生有效理解数学知识点.因此，运用几何直观可以实现轻松学习数学知识的目的.具体可从以下三方面着手：

一、对概念的理解更加清晰

小学生对于数学概念的理解和掌握具有一定的困难，这往往是数学概念自身的抽象性和逻辑性造成的.为此，数学教师在进行授课环节时，可利用几何直观，化抽象概念为具体，减少学生在理解上的难度，进而轻松、深刻地理解数学概念.下面以《面积的意义和面积单位》的教学片断为例，进行说明：

师：在之前课程的学习中我们已经有效了解了线段的含义、长方形的概念、正方形的特征，那么，接下来同学们仔细观察以上几幅图形（教师运用多媒体向学生展示两片形状各异的树叶图片），并向大家阐述自己的观点与感受.

生：第一片树叶较小，第二片树叶则很大.

师：接下来向学生展示两个正方形，让学生谈谈这两个正方形各自的特点.

生：两个正方形的大小不同.

师：回答得非常不错！同学们，无论是树叶，还是正方形、黑板、书本等等我们都可以将它们统一称作物体.那么用来表示这些物体的表面大小的概念就是——面积.大家自己思考一下，我们如何才能精准地判断两个不同物体的大小呢？

生：可以用眼睛观察.

生：可把物体分成若干小方格，方格数量越多，图形的面积就越大.

师：用方格子的方法可取吗？同学们，请你们看看上面这几幅图形.通过这几个图形的格子数量我们是不是就可以知道这些图形哪个比较大，哪个比较小呢？

生：这种方法是错误的，因为每个格子的大小不同，所以没办法进行合理比较.

师：好，同学们说得非常好，换句话说，也就是我们要想精准地得到图形的面积，就应该使用大小统一的方格，在这里，大小统一的方格也就是大小相等的方格.由此，我们可以准确理解国际上对于面积单位的定义，即为一定标准的正方形的面积大小.

作为数学教师应该懂得，数学是一个逐步构建思维体系的过程，在思维体系的构建中，只有不断从中进行体验和思考，才能在其中发现美妙的风景，并得到有效的感悟和体会，进而了解抽象的数学概念，建立稳固的熟悉思维体系.在上述教学环节的再现过程中，我们可以得知，数学教师在通过几何图形进行数学概念的讲解中，学生就可以更为直观地进行理解和掌握，进而轻松感受到面积的含义和面积单位的形成过程.

二、对规律的掌握更加直观

数学学科是小学科目中逻辑性最强且难度最大的学科，每个知识点之间都具有密切的联系.因此，教师在进行数学科目的教学过程中，可以根据其知识点间的联系入手，从其固有的联系中着手，给学生创设一定的数学教学情境，进而实现举一反三，活学活用的教学效果.下面以《三角形的三边关系》教学片断为例：

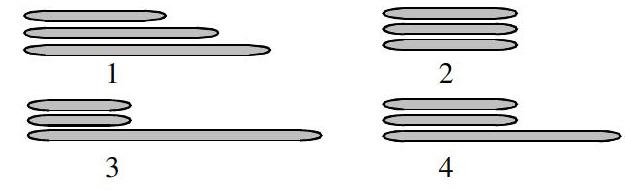
师：同学们，下面老师为大家准备几组长度不同的小棒，请大家仔细观察，动手操作，看看哪一组小棒能够围成三角形，并在旁边打上对号.

1. （3，4，5） 2. （3，3，3） 3. （2，2，6） 4. （3，3，5）

生：第一组小棒能围成一个三角形.

生：第二组小棒也能围成一个三角形.

生：第三组小棒不能围成三角形.

师：同学们，你们是怎么样得出这个结论来的呢？请把这个过程告诉老师，也和大家一起分享一下.

生：我用第二组小棒动手进行搭建的时候，发现2 cm的边长太短了，不能围成一个三角形.

师：同学们回答的非常好，也就是说，你们刚才所得出的结论是通过自己动手操作得来的，那么在操作的过程中，同学们关于组成三角形的条件你们领悟到了什么或者明白了什么道理？

生：要想组成三角形，必须要使三角形的其中任何两条边大于或者等于第三条边才可以.

通过利用几何图形进行三角形和其三边规律的讲解，教师不仅可以锻炼学生的动手操作能力，也可以有效引导学生进行积极思考，在头脑中加深印象，使学生对于三角形及其三边规律有更为形象的认识，以便加深理解和记忆.

三、对问题的解决更加轻松

在某些数学问题中，其已知条件相对复杂，对于小学生来说理解有些困难，如果仅凭教师的口头讲授则过于简练，不利于学生的消化理解，若在此过程中教师可以借助几何图形来解决，那么问题解决将会更加轻松，达到事半功倍的效果.

总之，教师在进行教学活动中，应敢于放手，利用几何直观方式将复杂的数学难题具体化、直观化，寻找最为简便的解题办法，提高学生的数学思维，进而有效探索数学规律，达到巧妙学习数学的目的.