一种新的符合度算法及其应用

张　慧　顾世梁　李　韬

1扬州大学农学院, 江苏扬州225009;2桐庐县农业技术推广中心, 浙江杭州311500



一种新的符合度算法及其应用

张慧1,2顾世梁1,*李韬1

1扬州大学农学院, 江苏扬州225009;2桐庐县农业技术推广中心, 浙江杭州311500

摘要:在总结分析了几种常用综合评价方法的基础上, 提出了一种反映观察值与理论值之间相似性的新算法——符合度。该算法就评价信息个体(观察值)与标准值(期望值)的马氏距离, 再由马氏距离转化为评价对象与标准的接近程度, 即符合度(r)。首先进行指标数(p)、相似度(r)与马氏距离(d)的模拟试验, 再通过曲面拟合的方法找出它们之间的关系模型。通过大量抽样试验, 验证符合度的次数分布与原先设定的符合度的良好对应关系, 说明模型的可行性与可靠性。以小麦RVA性状为指标, 利用该算法分析扬麦系统若干品种之间的接近程度, 并评价多变数复杂效应回归分析模拟试验的结果。符合度算法不需要数据标准化处理, 直接利用原始数据, 减少了计算工作量, 降低了因数据标准化处理方法不同而引起的评价结果差异, 同时由于不需要赋权, 排除了主观性的影响, 保证了信息的完整性以及评价结果的可靠性。

关键词:符合度; 综合评价; 计算机模拟; 马氏距离

本研究由国家农业信息化工程技术研究中心开放课题“小麦育种材料评价研究”项目资助。

This study was supported by open project of the National Agricultural Information Engineering Center.

第一作者联系方式: E-mail: zhanghui881007@126.com, Tel: 18606517137

在农学和生物学领域中, 常会遇到对研究对象的个体或群体进行评价的问题。所谓评价就是参照一定的标准,评判与比较研究对象的价值或优劣的一种认知和决策过程[1], 如育种过程中对目标品种(系)与参照品种优劣程度的评价、农作物产品品质分级标准的归属或模拟试验中统计数与参数(期望值、标准值)接近程度的评价。依据个体(或群体)的多个性状(指标), 以有利于从整体的角度客观、合理、公正地全面评价。所谓多指标综合评价方法, 就是把不同方面的多个指标的信息汇集成一个综合指标,来反映被评价对象的整体情况。这包括灰色关联度法、TOPSIS法、主成分分析法等[2-6]。多指标综合评价方法一般包括评价指标选择、构建指标体系、选择综合评价模型、

数据标准化处理、确定指标权重等过程, 从而综合分析得出结论[7-8]。目前可以用作综合评价方法考虑问题的侧重点不尽相同, 在实际应用中仍然存在各种缺陷和不足。其中, 数据标准化处理虽然能够解决不同指标(性状)因量纲和变异度的差异对评价具不同作用的问题, 但也会较大程度削弱不同指标所包含信息量的差异, 降低综合评价的可靠性[9-12]。另外, 在评价过程中, 由于评价体系的各个评价指标的重要程度不同, 大多数采用赋权的方式来体现。权重的确定主要应用主观赋权法和客观赋权法[13-14]。前者多根据专家经验; 后者则根据性状之间的相关关系或各性状的变异度(的倒数)或遗传力等, 而不同的权重系数,往往会导致很不相同甚至相反的评价结论, 这样就大大降低了评价的可靠性[15-20]。

随着人们对研究的不断深化, 所面临的评价对象日趋复杂, 人们对综合评价精准度的要求相应提高。符合度(conformity), 又称吻合度、接近度, 是指多变数观察样本与真值(理论值、期望值、经验值、标准值)之间或两个或多个多变数样本之间接近程度的量化指标。本文通过模拟试验, 产生不同类型的多变数样本与期望值(标准值)之间符合度量化关系的数据资料, 利用曲面拟合获得模拟试验的样本数据与符合度的关系模型。在此基础上, 通过进一步抽取一定条件下的大量样本, 计算符合度的次数分布。通过符合度分布的平均数、标准差等特征数值验证符合度计算过程的可行性和可靠性。这种新型的符合度关系能准确地衡量多变数样本与某些标准值之间的接近程度,也可用于评价模拟试验中统计估计值与设定参数之间接近程度, 从而可以量化评价不同统计分析方法的优劣。符合度指标衡量多变数样本个体之间的相似性, 还可用于相互比较评价或聚类分析等。

1　材料与方法

1.1抽样试验

若有多指标(多变数)样本X, 欲求算其中某一个体xi与某一标准值e之间的符合度(接近度、吻合度、恢复度) r。设X为具有p个指标(变数)和n个观察值(个体)的矩阵,标准值e是具有p个指标的向量。

这里1为n×1全是1的列向量, X的各行与e的各行为对应指标。xj=X(j)为X矩阵的第j列, 可视为该多变数样本的第j个个体。欲求样本中的个体x与e的接近程度r(x, e), 应尽量排除p个指标(变数)的量纲和变异度的影响, 同时也应考虑变数间相关性对符合度的作用, 寻找计算x与e的合适距离, 并由距离转化为符合度关系, 对这一过程需进行模拟和抽样试验。

假设一个标准值为e’ =(e1, e2,…, eP)。若X是一组正态或均匀分布的随机数, 可理解为随机向量x与e之间的相似性亦即符合度近乎为0。若x与e完全一样, 则它们之间的符合度即为1; 而x与e有一定程度的关联, 其符合度应是介于0和1之间的某个数值。当有50％的关联时,符合度应为0.5左右。关联程度越小, 符合度越趋近于0,关联程度越大, 符合度越趋于1。根据这一思路, 构建基于随机数x与e的中间变数y。

其中λ即为取值0到1间的符合度值。取公差为0.01的等差数列, 产生随机变数x并由式(1)得到相应的中间变数y。即当λ为0.1时, x与y存在0.1的相似性, 当λ为0.5时, x与y存在0.5的符合度, 以此类推, 从而通过中间变数y进而研究合适的距离和符合度的关系。

1.2距离选择

本研究中符合度的计算是由y和e之间的距离转化而来, 所以距离函数的选择对符合度函数的确定比较重要。常用的距离有欧氏距离、马氏距离、切氏距离和闵氏距离等。其中欧氏距离应用最为广泛, 但是它有明显的缺点,主要是受量纲与变异度的影响过大, 即变异度大的指标(变数)在距离计算中所占的分量比变异度小的指标(变数)大。若变数的变异度与距离计算的重要性不成比例, 则这样的距离就不能很好地反映它们的客观真实性。当对原数据进行标准化后, 则各指标对距离计算的分量完全相同,这在很多时候也并不恰当, 因为在很多综合评价过程中,并非所有指标对评价主体的重要性完全一致, 所得距离有时(或多数情况下)不能满足实际要求。欧氏距离的另一个缺陷是未能考虑多个变数间相关性对距离计算的作用,而相关程度越大, 欧氏距离与客观真实距离的偏差越大。最初我们也曾试验以欧式距离计算符合度的过程, 但在重抽样过程中(2.3节)出现明显偏差, 因而被否定。

马氏距离不受量纲和变异度的影响, 两点之间的马氏距离与原始数据的测量单位无关; 由标准化数据和中心化数据(即原始数据与均值之差)算出的两点间的马氏距离相同。更重要的是马氏距离还考虑了变数间相关性的作用, 所算距离更能体现个体间的远近关系。马氏(平方)距离公式如下:

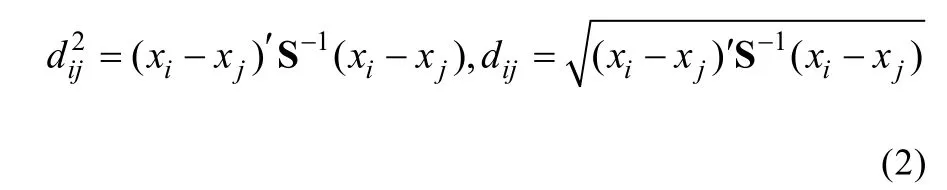
其中, xi和xj分别为第i和j个个体的p个变数(指标)所组成的向量, S为样本方差协方差矩阵。

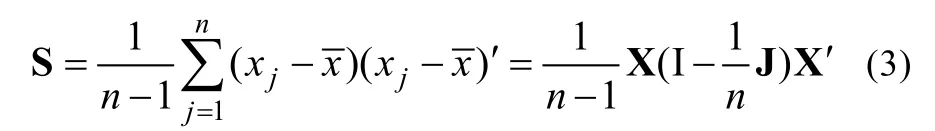
其中, I和J分别为n阶单位阵和全1阵。该S为p阶方阵, 对角线元素为各变数的方差, 非对角线元素为对应变数的协方差。它们包含了X变数在p维空间散布的信息, 因此又称为信息阵。而在本研究中, y与e之间的马氏平方距离(下文简记为马氏距离)如下:

在不同相似度(符合度)条件下随机抽样得到x并计算y与e之间的马氏距离, 距离随符合度有明显的负向趋势但波动较大。随着抽样次数的增加, 平均距离随符合度的变化趋势明显, 波动变小。试验表明, 30次抽样的平均距离与符合度的关系趋于稳定。可用于拟合反映两者关系的方程式。

1.3指标数设定

在大量随机的试验中发现, 试验数据X的量纲、变异度对计算马氏距离没有影响, 但指标数量(p)对马氏距离的尺度有较大影响。因而除了上述符合度与距离的抽样试验外, 我们还进行了指标数在距离计算过程中影响的抽样试验。考虑到大部分样本评价问题在5～25个指标之间,模拟试验的指标数在3～30之间, 本研究的指标数为3、5、10、15、20、25和30共7个水平, 了解指标数在距离和符合度之间关系的作用。从而根据抽样结果确定符合度依指标数和马氏距离的函数关系。

1.4Monte Carlo模拟研究

符合度依指标数和马氏距离的函数关系能否成立,还应在一定条件下重新抽样, 再根据函数关系式计算符合度数值, 大量抽样获取符合度的次数分布, 用于检验上述计算距离及符合度的过程是否符合实际。在指定符合度条件下随机抽取5000个样本, 代入函数关系方程算得符合度次数分布图。如果方程合适, 那么在给定符合度r的情况下, 将指标数、距离代入模型中计算所得r应该与设定结果一致, 从而证实符合度计算过程可行性。

1.5扬麦系统小麦品种间RVA值的相似度比较

选取2011年扬州大学农学院大田正季播种的扬麦系统小麦品种11个, 测定其面粉淀粉糊化特性, 参数有峰值黏度、糊化时间、低谷黏度、最终黏度和糊化温度(剔除2个次级性状回复值和崩解值, 消除方差协方差阵的奇异性, 马氏距离得以计算), 每品种3个重复。比较扬麦系统的11个品种之间的相似程度并利用其符合度进行聚类分析。

1.6统计数与模拟设定的符合度比较

在许多模拟试验中, 要评价模拟结果的优劣, 直观比较不能客观反映真实情况。对一个多变数复杂效应回归分析模拟试验中效应的回归估值与期望值之间的接近程度以量化的形式表示出来, 可用于客观准确的评价模拟试验。

2　结果与分析

2.1符合度与马氏距离的关系

根据设定的随机变量、中间变量和符合度的关系, 采用随机抽样的方式计算符合度与马氏距离的关系, 单次抽样(每一符合度条件下只抽一个随机向量)所得距离与符合度有明显的负向趋势但波动较大。随着抽样次数的增加, 波动变小。在符合度很低时, 距离较大, 随着符合度的增加, 距离变小, 当两者非常接近时, 距离趋于0。距离随符合度的增加而单调降低, 其散点图成线性排列, 但并非简单的直线, 在符合度的高端, 曲率明显。模拟试验中发现, x和/或e的数值乘以一定的倍数, 这种关系并无改变, 即符合度与马氏距离的关系不随量纲与变异度变化而改变, 适合各种类型多变数样本的评价。

显然, 马氏距离可很好地描述个体与标准值之间的符合程度。但由于马氏距离会大于1或远大于1。而我们更希望得到的符合度数值介于0～1之间, 0代表没有相似性, 1代表完全符合。随着距离的增大, 符合度越来越小,误差亦有所增加(图1, 前述散点图X、Y轴互换)。在实际使用中, 我们不能事先得到符合度, 必须先计算样本(平均数)与目标值之间的距离, 再确定符合度与距离的数量关系。

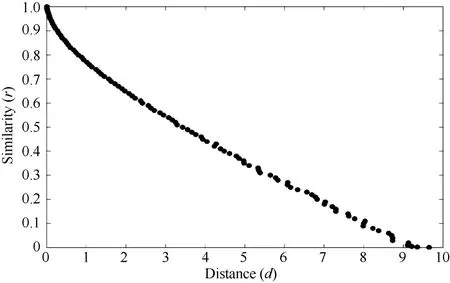
图1　符合度依马氏距离关系图Fig. 1　Relationship between Mahalanobis distance and similarity

2.2符合度函数

由于指标数也在很大程度上影响距离与符合度的关系, 利用曲面拟合方式, 寻找指标数p, 马氏距离d与符合度r的函数关系式, 根据数据点在三维空间中的分布情况和各类变数方程的特点, 经大量模型选择和比较分析,确定如下模型:

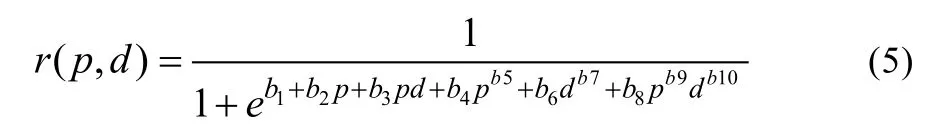
本研究选择C-E算法进行曲线、曲面拟合[21-22], 该算法无需提供导数与偏导数, 无需提供特定初值, 实现最优拟合的能力较强。拟合结果如图2, 各参数值及显著性t测验值见表2。

2.3Monte Carlo模拟研究

随机抽取5000个样本X(p=20), 按y=(1–λ)x+λe计算马氏距离d以及由d和p通过式(5)计算获得5000个符合度r, 绘成次数分布图。若符合度计算方程合适, 那么在

给定符合度(λ)情况下, 将指标数值、检测值代入模型中计算所得r应该与设定结果一致, 且在中等程度符合度时,其符合度的抽样分布接近于平均数为0.5的正态分布。如表2和图3所示, 当设定λ=0.5时, 其r分布平均数为0.502, 标准差为0.0849, 分布接近正态, 准确度高, 误差小。除了很小符合度(λ=0.05)时略有偏差外, r的分布与设定情况充分符合, 证明该方法的可行性。

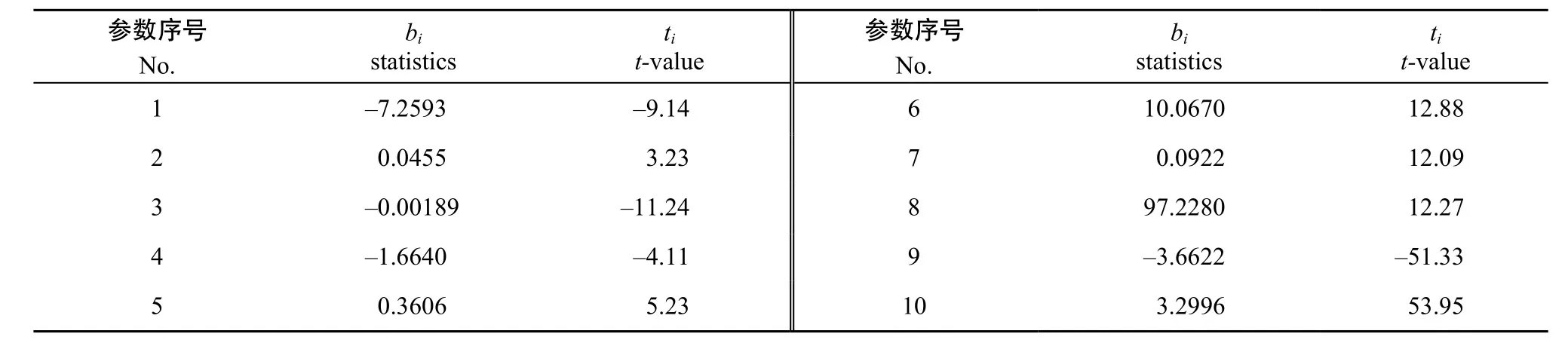
表1　模型拟合统计数及测验Table 1　Simulated conformity function and its statistics

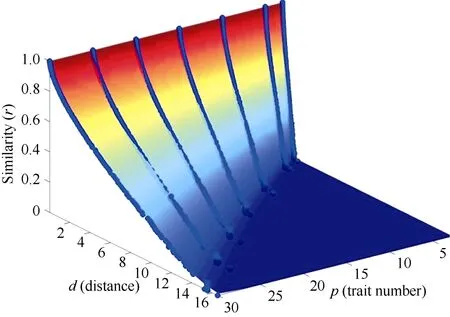
图2　模型拟合曲面图Fig. 2　Surface fitting for conformity with variables and distance

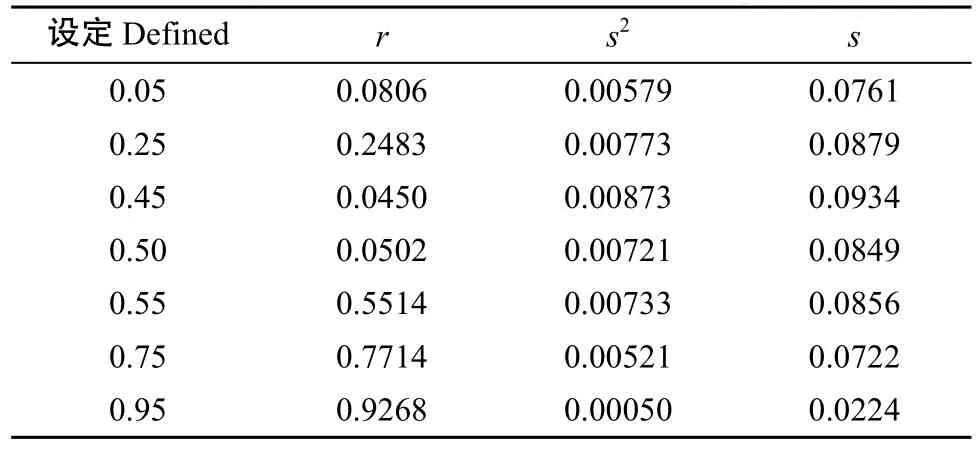
表2　Monte Carlo抽样试验符合度分布的平均值(r)、方差(s2)和标准差(s)Table 2　Means (s), variance (s2), and standard deviation (s) of conformity distribution in Monte Carlo experiment

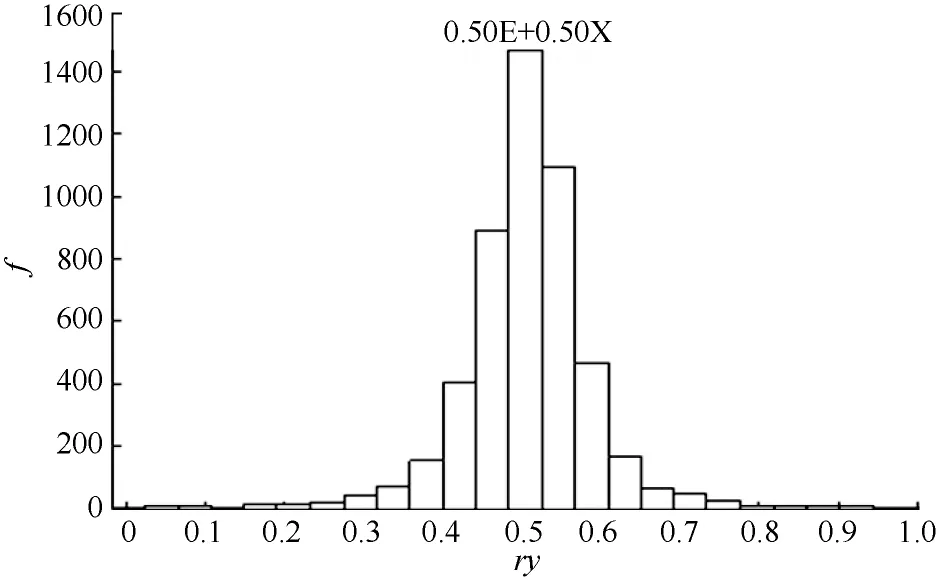
图3　与标准e的符合度为0.5的检验图Fig. 3　Histogram of conformity under similarity of 0.5 e

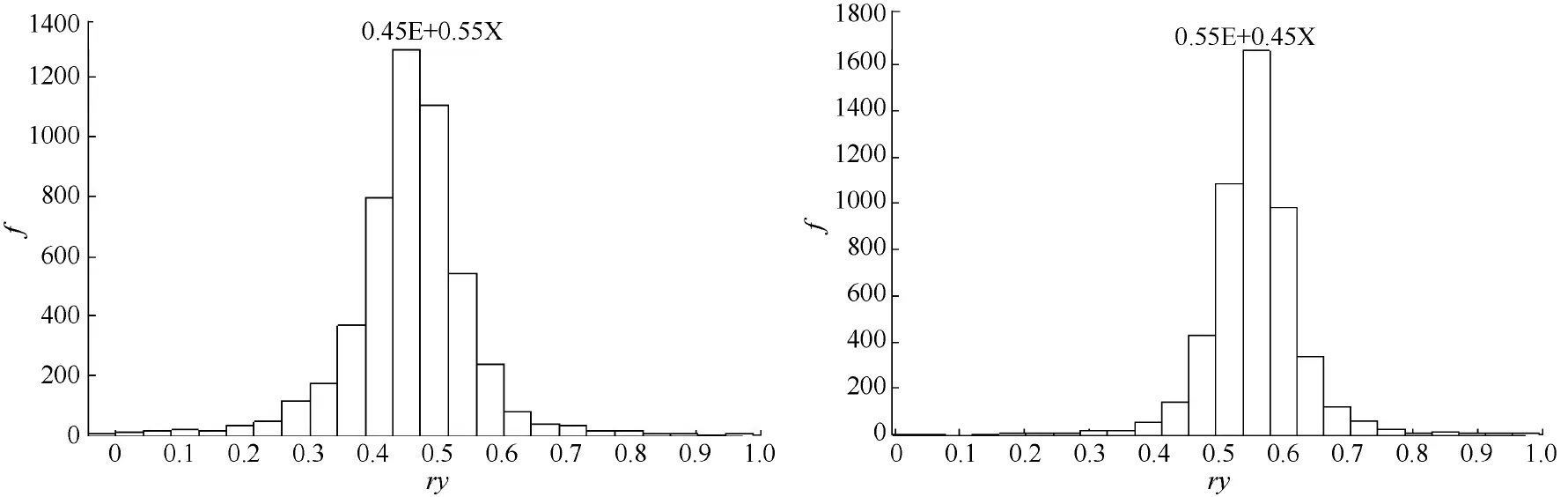
图4　与标准e的符合度为0.45 (左)、0.55 (右)的次数分布图Fig. 4　Histogram of conformity under similarity conditions 0.45 (left) and 0.55 (right)

由图4和图5可见, 各符合度分布均以设定值为中心,但随着设定符合度偏离0.5, 它们的分布呈现左偏或右偏。符合度较高, 甚至接近于1时, 分布相对集中, 误差较小; 在符合度接近于0时, 由于抽样数据的随机性, 符合度形成明显的偏态分布, 说明对于评价对象与目标之间符合度较低的情形, 符合度的估计具有一定的偏差。

检验证明, 按一定符合度给出的随机数据计算所得的符合度的分布结果与期望的结果相吻合, 该符合度关系式能够准确地反映实际符合度关系。

3　符合度算法的应用实例

3.1扬麦系统中各品种RVA值的相似度比较

最合理的计算马氏距离的方差协方差阵应为误差方差协方差阵Se, 但误差偏小, 只能用总方差协方差阵S。首先利用全部的原始数据计算出该样本的方差协方差阵,用于计算马氏距离d。

将选取的扬麦系统11个品种的RVA值分别代入马氏距离计算公式, 得到品种之间的马氏距离d (表3), 由式(5)计算符合度, 得出RVA值之间的相似程度(表4)。

以RVA特征值计算扬麦系统11个材料间的相似性可以较好地反映这些材料间的RVA特征之差异。如扬麦5与扬麦16的RVA特征值最为接近, 扬麦10号与扬麦14的RVA特征值也很接近, 其相对接近的还有扬麦9号与扬麦158。以符合度作为相似度值系统聚类(图6)。相似系数在0～1之间, 可较好地避免其他类型的相似系数出现负数的情况, 更好地体现个体间的相似性。同时也可避免用距离等不相似系数出现大于或远大于1的数值, 对个体间不相似程度的描述有一定程度的扭曲。

3.2符合度在回归模拟试验中的应用

图7显示一个复杂系统新型回归分析方法, 即重复筛选回归(ISR)模拟。图中前后对角线左侧为设定的效应真值, 右侧对应位置为100次模拟试验回归估计的平均值。方柱位置代表效应项(对角线位置为主效、非对角线位置为互作项)对应的标记项, 方柱的高度为效应值(以方柱顶上的数值表示)。可以看出, 这些效应项的回归估计值非常接近真值。

效应项的回归估值与真值的接近程度或称效应的恢复度如何衡量, 客观的判断离不开数量化指标的协助。本试验设定的效应真值e以及100次筛选逐步回归的模型试验的回归估值平均数见表5, 建立了方差-协方差阵S(未列出)。计算得出d=0.2510, r=0.9089, 该数值较高, 说明重复筛选回归分析的效应估计能够较好地符合设定真值。

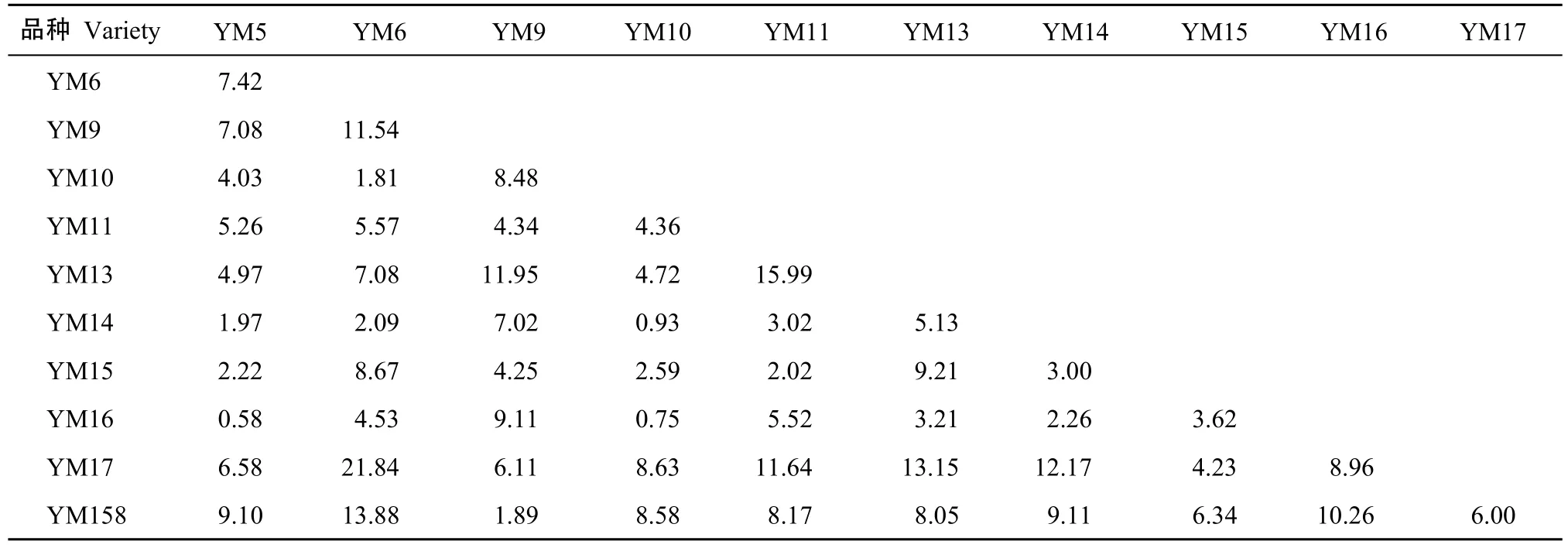
表3　扬麦系统(YM)各品种RVA值之间的马氏距离dTable 3　Distance between the varieties based on their RVA characters

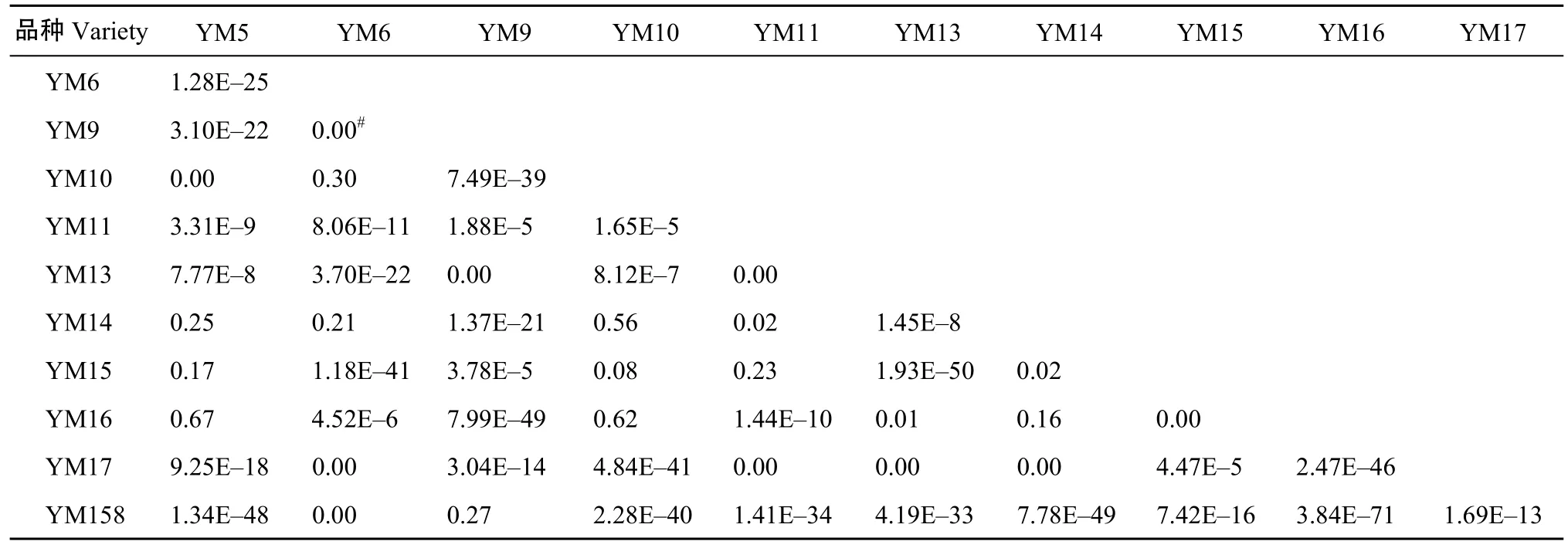
表4　扬麦系统(YM)各品种间RVA的相似度(符合度)Table 4　Conformities among RVA parameters of YM varieties

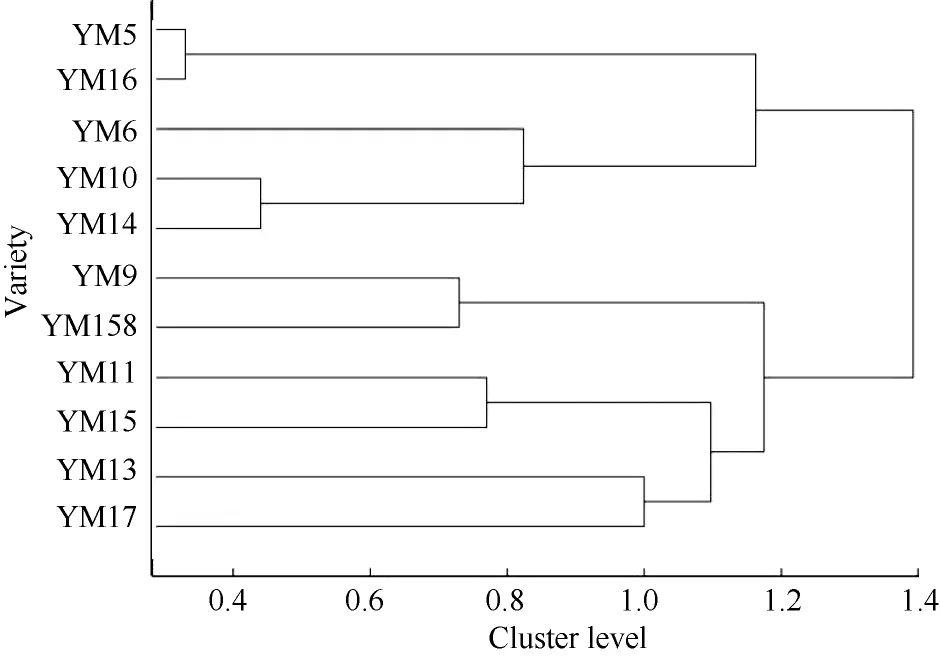
图6　扬麦系统11个小麦品种的RVA值据符合度聚类Fig. 6　Hierarchical clustering dendrogram for the 11 varieties according to conformity

4　讨论

4.1符合度的特点

本研究提出的符合度新算法是一种量化样本间或者样本与标准之间接近程度的方法。虽然马氏距离也可较好地描述个体与标准值之间的符合程度, 但由于马氏距离会大于或远大于1, 更合理的符合度数值应介于0～1之间, 0代表没有相似性, 1代表完全符合, 这与符合度的概念更加相称, 量值更加准确。另外, 基于0～1之间符合度数值的聚类分析等多变数分析比用基于距离的分析能更好地体现个体之间的亲疏远近, 因为聚类等多变数分析将较大程度地过度强化大数值的作用而忽略小数值的作用。

比较现有的综合评价方法, 该算法的优势在于无需数据标准化处理, 以原始数据直接计算, 简化了计算, 也降低了因无量纲化处理方式不同而导致的结果差异; 另外, 符合度算法综合考虑各指标的信息, 指标没有重要程度之分, 不需要赋予权重, 保证了原始信息的完整性, 也排除了主观赋权的随意性[14-15]。

4.2缺失值的处理

在实际数据的应用中往往会出现某个指标缺失的情况, 缺值计算的主要困难在于此时的方差协方差矩阵S会出现异常或偏差, 本研究提出了如下相对简单的处理缼值数据的方差协方差阵修正公式。

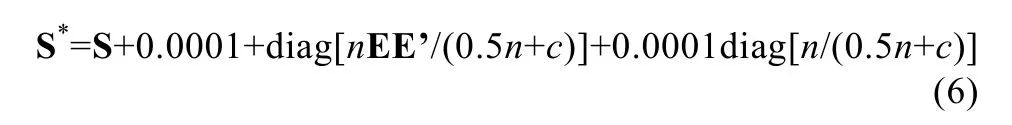
式中, n为数据总个数, c是非缺值数据个数。这主要在于降低有缼值指标(变数)在多变数评价中的影响力。

多指标系统的样本观察值(测定值、样本值)与标准值(理论值、期望值)之间的吻合程度总体上比较复杂。我们尝试用其他多种计算符合度、恢复度的方法, 但效果不如本文提出的符合度计算方法, 该算法基本实现了客观合理地描述样本与理论值或个体相互间符合度的数量化计算。当然, 用单个的数值衡量其符合度仍有可能失之偏颇。准确的综合评价有时仍需辅以另外的一个或多个指标。

4.3变数相关程度的影响

在本试验中, 随机变数X服从正态(或均匀)分布, 得出指标数(p)和马氏距离(d)计算符合度的函数关系, 也得到了重抽样试验的验证。但当变数间有很强的相关关系时,符合度与马氏距离等的关系式会有一定程度的偏差。

4.4方差协方差矩阵选择

马氏距离的计算取决于观察样本的方差协方差阵S,采用何种方差协方差也至关重要。当n个多变数观察个体没有重复观察值时, 总的样本方差协方差阵是唯一的选择, 但这事实上并不合理。当观察个体有重复观察值时,总的方差协方差阵(S)可分解为组间(B)和组内(W)两部分(S=B+W)。而用于评价个体相似性、符合度计算的合适的马氏距离应选择W, 这代表观察样本去除个体间差异的本质的内在的信息阵, 可更好地描述个体间的相似程度。

4.5基于表型或基因型的聚类

聚类分析可根据试验材料的表型, 也可根据基因型进行。两种聚类结果的一致性取决于基因型与表型性状之

间的一致性。若注重于品种的整体相似性, 应以能综合反映品种特性的基因型数据的聚类更为合适; 若就某些农艺性状的表现对品种分类, 则依据这些农艺性状聚类更为合适, 因为在大多数情况下, 获得的基因型数据与表型数据并不对应。本研究并未对与小麦面粉RVA性状相关的基因型进行测定, 根据RVA表型计算符合度(相似性)并据此聚类, 这与品种整体特性的相似性和分类特性不一定等价。

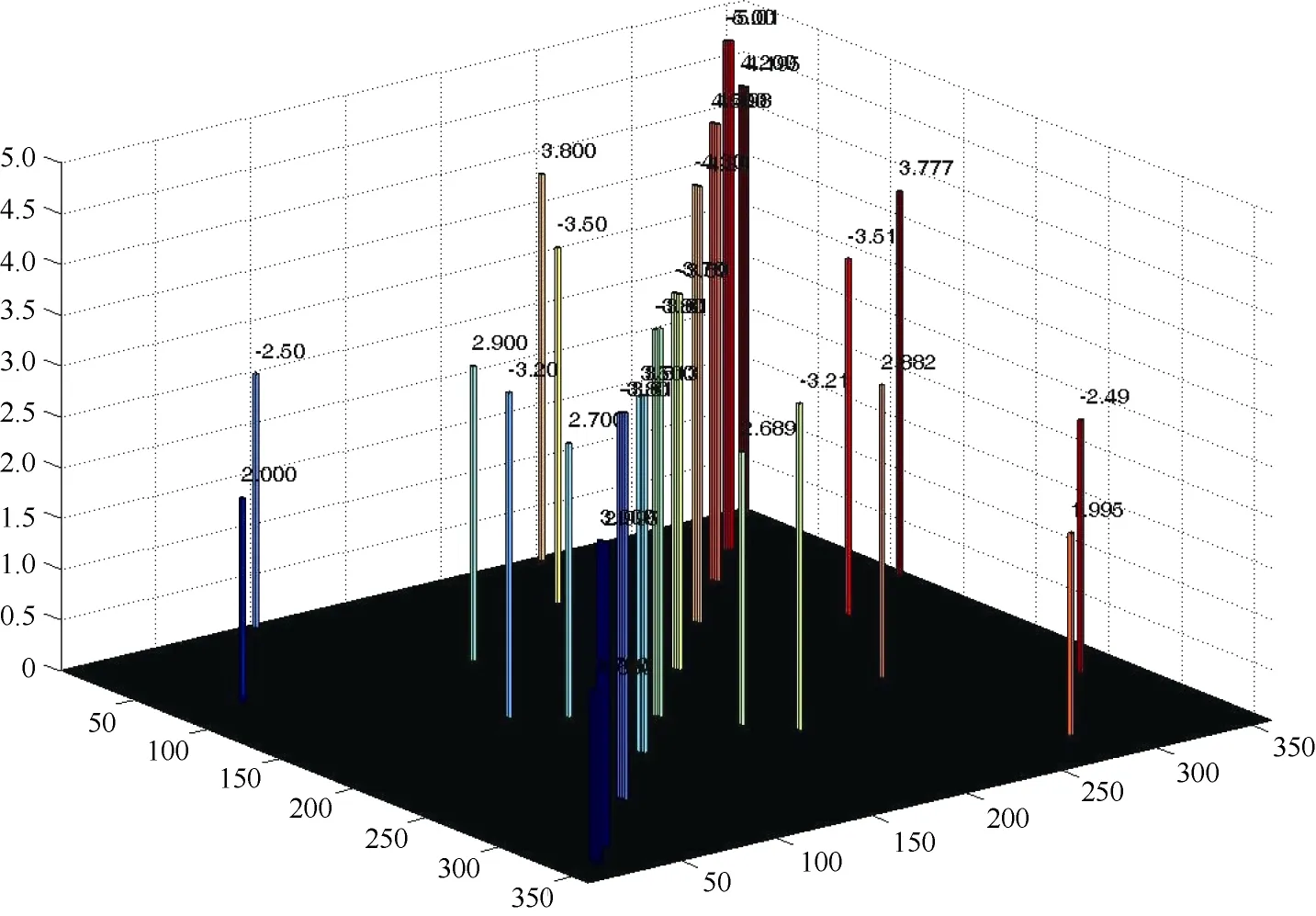
图7　效应真值与估计值的比较Fig. 7　Comparison between true effects and estimations

表5　回归模拟试验的效应值、真值(e)和回归估计平均数()Table 5　Effect estimates and corresponding parameters

表5　回归模拟试验的效应值、真值(e)和回归估计平均数()Table 5　Effect estimates and corresponding parameters

序号No.效应项Effect 　e x 　序号No.效应项Effect 　e x 1 　a 　100.0 　99.986 　10 　X320　　–5.0 　　–5.012 2 　X20　1.7 　1.689 　11 　X355　4.2 　4.203 3 　X35　3.0 　3.021 　12 　X35–X280　2.0 　1.995 4 　X80　　–3.8 　　–3.813 　13 　X100–X335　　–2.5 　　–2.490 5 　X125　3.5 　3.514 　14 　X130–X180　2.7 　2.689 6 　X160　　–3.8 　　–3.808 　15 　X110–X195　　–3.2 　　–3.212 7 　X205　　–3.7 　　–3.694 　16 　X220–X305　　–3.5 　　–3.510 8 　X250　　–4.3 　　–4.297 　17 　X145–X265　2.9 　2.882 9 　X290　4.5 　4.503 　18 　X250–X355　3.8 　3.777

References

[1] 顾基发. 评价方法综述. 见: 许国志. 科学决策与系统工程——中国系统工程学会第六次年会论文集.北京: 中国科学技术出版社, 1990. pp 5–7 Gu J F. Evaluation method review. In: Xu G Z ed. Scientific Decision-Making and System Engineering. Proceedings of 6th Conference of the Systems Engineering Society of China. Beijing: China Science and Technology Press, 1990. pp 5–7 (in Chinese)

[2] Chen S J, Hwang C L, Hwang F P. Fuzzy Multiple Attribute Decision Making: Methods and Applications (Lecture Notes in Economics and Mathematical Systems), Springer-Verlag, 1992. pp 163–287

[3] Hwang C L, Masud A S M. Multiple Objective Decision Making—Methods and Applications. New York: Springer-Verlag, Berlin-Heidelberg, 1979. pp 2–325

[4] Peng Y X, Yi S Z. The multi-hierarchy integrated evaluation method of enterprise’s credit grade. In: Proceedings of ISAHP, 1999. pp 125–128

[5] Savoy J. Statistical inference in retrieval effectiveness evaluation. Inf Proc & Manag, 1997, 33: 495–512

[6] Yuan Z, Wang H, Liu L Z, Liang T. Researching the comprehensive use of fuzzy comprehensive evaluation and Markov chain// IT in Medicine & Education, 2009. ITIME’09. IEEE Interna-

tional Symposium on. IEEE, 2009. pp 476–479

[7] 陈凯华, 张孝远. 模糊综合评价模型的改进及应用. 甘肃科学学报, 2006, 18(3): 111–115 Chen K H, Zhang X Y. Application of the improved fuzzy comprehensive appraisal model. J Gansu Sci, 2006, 18(3): 111–115 (in Chinese with English abstract)

[8] 程鹤, 耿双军. 模糊综合评价的改进模型. 统计与决策, 2007, (13): 136–137 Cheng H, Geng S J. The improved model of fuzzy comprehensive evaluation. Stat & Decision, 2007, (13): 136–137 (in Chinese)

[9] 田钦谟. 模糊综合评价中的若干问题. 模糊系统与数学, 1996, 10(2): 62–69 Tian Q M. Several problems in fuzzy comprehensive evaluation. Fuzzy Systand Math, 1996, 10(2): 62–69 (in Chinese with English abstract)

[10] 王宗军. 综合评价的方法、问题及其研究趋势. 管理科学学报, 1998, 1(1): 73–79 Wang Z J. On the methods, problems and research trends of comprehensive evaluation. J Manag Sci China, 1998, 1(1): 73–79 (in Chinese with English abstract)

[11] 杜栋, 庞庆华. 现代综合评价方法与案例精选. 清华大学出版社有限公司, 2005 Du D, Pang Q H. Modern Comprehensive Evaluation Method and Case Selection. Beijing: Tsinghua University Press Co., Ltd. 2005 (in Chinese)

[12] 马立平. 现代统计分析方法的学与用(三): 统计数据标准化——无量纲化方法. 北京统计, 2000, (3): 34–35 Ma L P. Learning and using in analysis methods of modern statistical: (3) Statistical data standardization, dimensionless method. J Beijing Stat, 2000, (3): 34–35 (in Chinese)

[13] 叶宗裕. 关于多指标综合评价中指标正向化和无量纲化方法的选择. 浙江统计, 2003, (4): 24–25 Ye Z Y. The choice of multi-index comprehensive evaluation index in positive and dimensionless. J Zhejiang Stat, 2003, (4): 24–25 (in Chinese)

[14] 易平涛, 张丹宁, 郭亚军, 高立群. 动态综合评价中的无量纲化方法. 东北大学学报(自然科学版), 2009, 30: 889–892 Yi P T, Zhang D N, Guo Y J, Gao L Q. Study on dimensionless methods in dynamic comprehensive evaluation. J Northeastern Univ (Nat Sci), 2009, 30: 889–892 (in Chinese with English abstract)

[15] 张卫华, 赵铭军. 指标无量纲化方法对综合评价结果可靠性的影响及其实证分析. 统计与信息论坛, 2005, 20(3): 33–36 Zhang W H, Zhao M J. The influence of undimensionalization on the reliability of comprehensive evaluation results and an empirical analysis. Stat & Inf Forum, 2005, 20(3): 33–36 (in Chinese with English abstract)

[16] 孙威武. 评价因素权重向量的确定方法. 统计与决策, 2002, (7): 17–18 Sun W W. The method to determine the weights of evaluation factors vector. Stat & Decision, 2002, (7): 17–18 (in Chinese)

[17] 王雪标, 龚兆仁, 郑晓薇. 线性综合评价函数的充要条件及权系数的确定. 系统工程理论与实践, 2000, 20(10): 58–62 Wang X B, Gong Z R, Zheng X W. Linear synthetical evaluation function and the determination of its weighting coefficients. Syst Eng-Theory & Practice, 2000, 20(10): 58–62 (in Chinese with English abstract)

[18] Grabowski M, Wallace W A. An expert system for maritime pilots: Its design and assessment using gaming. Manag Sci, 1993, 39: 1506–1520

[19] Guo Y J, Yao Y, Yi P T. Method and application of dynamic comprehensive evaluation. Syst Eng-Theory & Practice, 2007, 27(10): 154–158 (in Chinese with English abstract)

[20] 王大将, 周庆敏, 常志玲, 孙洁. 一种新的多指标综合评价方法. 统计与决策, 2007, (7): 137–138 Wang D J, Zhou Q M, Chang Z L, Sun J. A new method of multi-index comprehensive evaluation. Stat & Decision, 2007, (7): 137–138 (in Chinese)

[21] 顾世梁, 万林生, 黄丽娟, 王文平. 曲线和曲面拟合的改进缩张算法. 作物学报, 2007, 33: 583–589 Gu S L, Wan L S, Huang L J, Wang W P. Improved contraction-expansion algorithm for curve and surface fitting. Acta Agron Sin, 2007, 33: 583–589 (in Chinese with English abstract)

[22] 顾世梁, 惠大丰, 莫惠栋. 非线性方程最优拟合的缩张算法. 作物学报, 1998, 24: 513–519 Gu S L, Hui D F, Mo H D. The optimal fitting of nonlinear equation with contraction-expansion algorithm. Acta Agron Sin, 1998, 24: 513–519 (in Chinese with English abstract)

URL: http://www.cnki.net/kcms/detail/11.1809.S.20151013.1508.004.html

A New Algorithm for Conformity and Its Application

ZHANG Hui1,2, GU Shi-Liang1,*, and LI Tao1
1Agricultural College of Yangzhou University, Yangzhou 225009, China;2Agricultural Extension Station of Tonglu County, Hangzhou 311500, China

Abstract:This article proposed a new algorithm of conformity using original data to calculate similarities between the target object and the expected value based on the Mahalanobis distance, providing an objective and reasonable analysis. Firstly, simulation experiments were conducted to obtain Mahalanobis distance (d) related to number (p) of different variables (traits) and similarity (r). Then, a surface fitting method was used to establish the function relationship between conformity (r) and index number (p), as well as Mahalanobis distance (d). Monte Carlo experiment for frequency distribution of conformity verified its good performance of the relationship model. The simulation results fully validated the feasibility and reliability of the model. Conformity algorithm was applied to calculate the similarity of a panel of Yangmai wheat varieties released in recent years referring to RVA parameters. The assessment of simulated multivariate regression for complex effects was also conducted. This study showed that conformity algorithm using raw data directly instead of standardized data reduces the work load and decreases inconsistency in similarity assessment with different data processing methods. In addition, conformity algorithm does not need weight assignment to each trait, thus can eliminate potential subjective impacts on traits or data and guarantee integrity of information and reliability of evaluation results.

Keywords:Conformity algorithm; Comprehensive evaluation; Computer simulation; Mahalanobis distance

收稿日期Received(): 2015-02-05; Accepted(接受日期): 2015-09-06; Published online(网络出版日期): 2015-10-13.

通讯作者*(Corresponding author): 顾世梁, E-mail: slgu@yzu.edu.cn, Tel: 0514-87979358

DOI:10.3724/SP.J.1006.2016.00141