一种复合算法的装配序列规划方法

刘恩福，刘　博，刘晓阳，李　伊

(河北科技大学机械工程学院，河北石家庄　050018)



一种复合算法的装配序列规划方法

刘恩福，刘博，刘晓阳，李伊

(河北科技大学机械工程学院，河北石家庄050018)

摘要：针对复杂产品装配规划的组合爆炸和盲目搜索难题，提出一种复合算法解决装配序列规划问题的方法。复合算法首先采取多色集合形式化推理获取足够数量的可行装配序列，并将可行装配序列作为遗传算法的初始种群；然后，通过遗传算法和蚁群算法将人的模糊知识融入规划过程中求精确解；最后，通过实例验证了复合算法的可行性。

关键词：计算机辅助制造；装配序列规划；复合算法；多色集合；遗传算法；蚁群算法

E-mail：liuef@hebust.edu.cn

刘恩福，刘博，刘晓阳，等.一种复合算法的装配序列规划方法[J].河北科技大学学报,2016,37(1):52-57.

LIU Enfu，LIU Bo，LIU Xiaoyang，et al.An assembly sequence planning method based on composite algorithm[J].Journal of Hebei University of Science and Technology,2016,37(1):52-57.

产品装配序列规划是产品设计开发过程中的重要环节，装配序列规划的结果能够直接影响产品的装配质量。因此，计算机辅助装配序列规划技术对于缩短装配时间和减小装配成本等方面具有重要意义，是目前国内外研究的热点。

计算机辅助装配序列规划的研究始于20世纪80年代，常见的装配序列规划方法有基于装配优先约束关系的装配序列生成方法、基于组件识别的装配序列求解方法、基于矩阵运算的方法、基于知识的求解方法、拆卸法等[1]。

20世纪末，随着研究的深入，人们开始将各类智能优化算法如遗传算法、蚁群算法、模拟退火算法、神经网络算法等应用到装配序列规划中，这些智能优化算法可以良好地克服传统方法中存在的组合爆炸问题和装配知识的局限性问题。遗传算法[2-6]是目前在装配序列规划中应用最为广泛的算法，但遗传算法在解决装配序列规划问题时具有全局收敛能力较差和存在大量冗余迭代的问题，而且要求初始种群必须为可行序列，初始设置较复杂；蚁群算法[7-12]在装配序列规划问题中也有着广泛的应用，但它具有初始信息素累积较慢，计算效率较低且容易局部收敛的缺点；多色集合理论体系[13-15]是一种新兴的系统理论和信息处理的数学工具，在近几年也被用来解决装配序列规划问题，但它仅能提供可行装配序列，需要进一步优化才能获得最优装配序列；混合蛙跳算法[16]和粒子群算法[17-19]已经成功地应用于复杂产品装配序列规划领域，但混合蛙跳算法在后期的收敛速度较慢，粒子群算法也存在着容易陷入局部最优解的问题。

针对以上问题，本文提出一种基于复合算法进行装配序列规划的方法。

1复合算法的基本原理

该复合算法利用多色集合形式化推理算法，并借鉴遗传算法和蚁群算法推理过程快速生成最优装配序列。图1为复合算法的原理图。

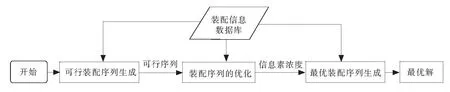
图1　复合算法基本原理图Fig.1　Basic principle of composite algorithm

2复合算法研究

2.1　可行装配序列生成

多色集合形式化推理算法能够快速求出可行装配序列，该算法在面对复杂产品时可以较大程度上缩小求解空间，有效降低计算的复杂性，所以，复合算法利用多色集合形式化推理算法来进行可行装配序列的生成。

2.1.1装配关系模型

多色集合形式化推理算法以装配约束关系方程组作为筛选可行装配序列的充要条件。装配约束关系方程组包括定位关系方程组和干涉关系方程组，它们分别由定位关系模型和干涉关系模型求取得出[20]，如图2和图3所示。

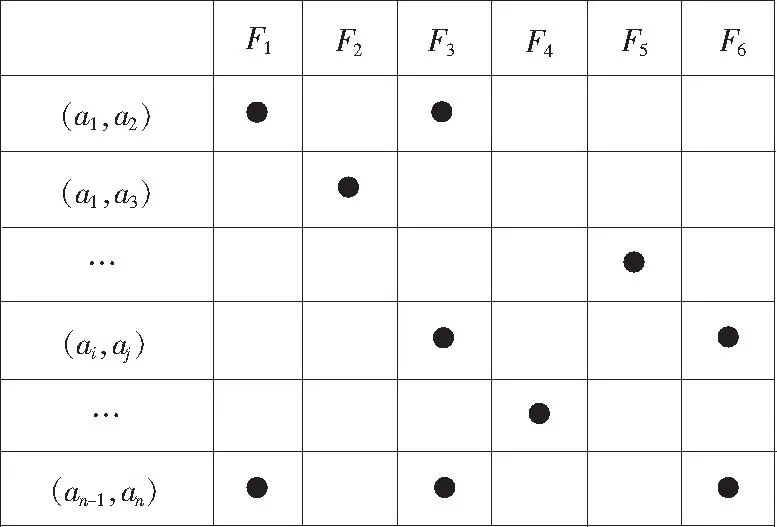
图2　定位关系模型Fig.2　Location relationship model

图3　干涉关系模型Fig.3　Interference relationship model

图2和图3中，(ai,aj)表示零件j对零件i的逻辑关系；F1~F6表示零件在x,y,z方向平动、转动的定位关系；F7~F12表示零件在±x,±y,±z方向的干涉关系；·表示存在定位关系或者干涉关系。

2.1.2定位关系方程的建立

定位关系方程是由定位元件(能够确定某一零件在装配体中正确位置的零件集)按一定的逻辑关系组成的关系式，定位关系方程的值代表零件在装配时能否定位。

定位关系方程组的求取算法：

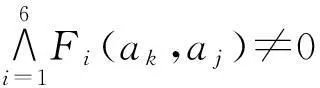
3)若B(ak)=aj∧am，且B(ak)=aj∧al，则B(ak)=aj∧(am∨al)。

其中：ai代表零件i是否安装，如果零件i已安装，则ai=1，如果零件i未安装，则ai=0；B(ai)的值代表零件i的定位状态，B(ai)=1代表零件i在装配时能够定位，B(ai)=0代表零件i在装配时不能定位。

2.1.3干涉关系方程的建立

干涉关系方程是由1组干涉某一零件进入装配区间的其他零件按照一定的逻辑关系组成的关系式，干涉关系方程的值代表零件在装配时是否会发生干涉。

干涉关系方程组的求取算法如下：

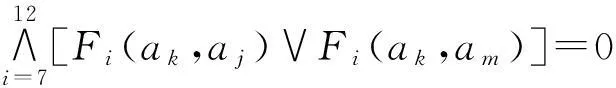
3)若W(ak)=aj∧am，且W(ak)=aj∧al，则W(ak)=aj∧(am∨al)。

其中W(ai)的值代表零件i的干涉状态，W(ai)=1代表零件i在装配时会与其他零件发生干涉，W(ai)=0代表零件i在装配时不会与其他零件发生干涉。

2.2　可行装配序列优化

基于多色集合形式化推理生成的可行装配序列，通过对遗传算法的变异操作进行改进，快速生成新的可行装配序列，并对可行装配序列进一步优化。

2.2.1适应度函数建立

适应度函数的建立直接影响着新的可行装配序列生成效率和质量。优秀的装配序列应具有较低的装配成本、较短的装配时间及较高的装配质量，因此，本文主要以装配方向的改变次数、装配工具的更换次数以及装配体的稳定性这3项评价指标来构建适应度函数。

适应度函数的构建方法如下：

f(s)=ω1vc-ω2vt-ω3vd+vp，

(1)

vp为装配序列的几何可行性，取

ω1,ω2,ω3为权重系数。

2.2.2改进变异算法

为了保证新的可行装配序列快速生成，本文提出一种新的变异方法：选取1个父代个体，从这个个体中随机选择1个零件，对选择零件后的序列利用多色集合形式化推理部分的算法重新进行排序，由于多色集合形式化推理算法具有快速性和准确性，可以有效生成新的可行序列，这样就免去了对生成序列进行可行性判断的步骤，有效提高了迭代效率。

2.2.3可行装配序列优化终止条件

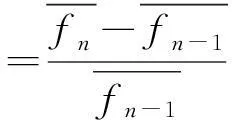
2.3　最优装配序列生成

该复合算法借鉴蚁群算法使装配序列优化过程快速收敛，生成最优装配序列。

2.3.1状态转移概率函数的建立

在构建装配序列的过程中，从基础件出发，根据状态转移概率选择下一级装配零件，状态转移概率由信息素、装配方向和装配工具决定。

状态转移概率函数的构建方法如下：

(2)

2.3.2信息素初始值设定

信息素初始值设计如下：

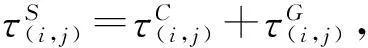
(3)

3复合算法的实现流程

该复合算法的实现流程如图4所示。

图4　复合算法流程图Fig.4　Flow chart of the composite algorithm

4实例验证

为了验证算法的可行性，以图5所示装配体为例，使用Visual C++ 6.0分别对复合算法、遗传算法、蚁群算法进行编程实现。其中，设定遗传算法的初始种群数N=5，变异概率为1，最小遗传迭代次数I=10，最小进化率P=0.05，蚂蚁数量M=5，全局信息素蒸发率为0.3。

图5　轴系部件Fig.5　Shaft parts

通过多色集合形式化推理算法对装配体进行可行装配序列生成，得到5个可行装配序列，分别是：

1)a1→a3→a2→a4→a5→a6；

2)a1→a3→a2→a5→a4→a6；

3)a1→a3→a2→a5→a6→a4；

4)a1→a3→a4→a2→a5→a6；

5)a1→a4→a3→a2→a5→a6。

运行程序所得的最优装配序列为a1→a3→a2→a5→a6→a4。图6为3种算法中各代种群的平均适应度函数值图。

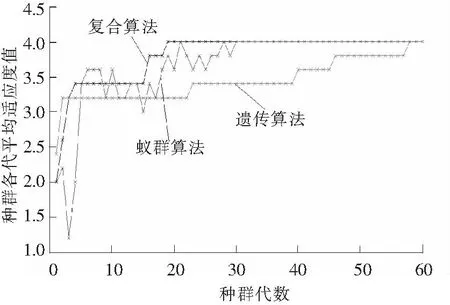
图6　种群各代平均适应度值Fig.6　Fitness value of each generation

同时，分别采用不同的种群数量和不同的蚂蚁数量对3种算法进行比较，其结果如表1所示。

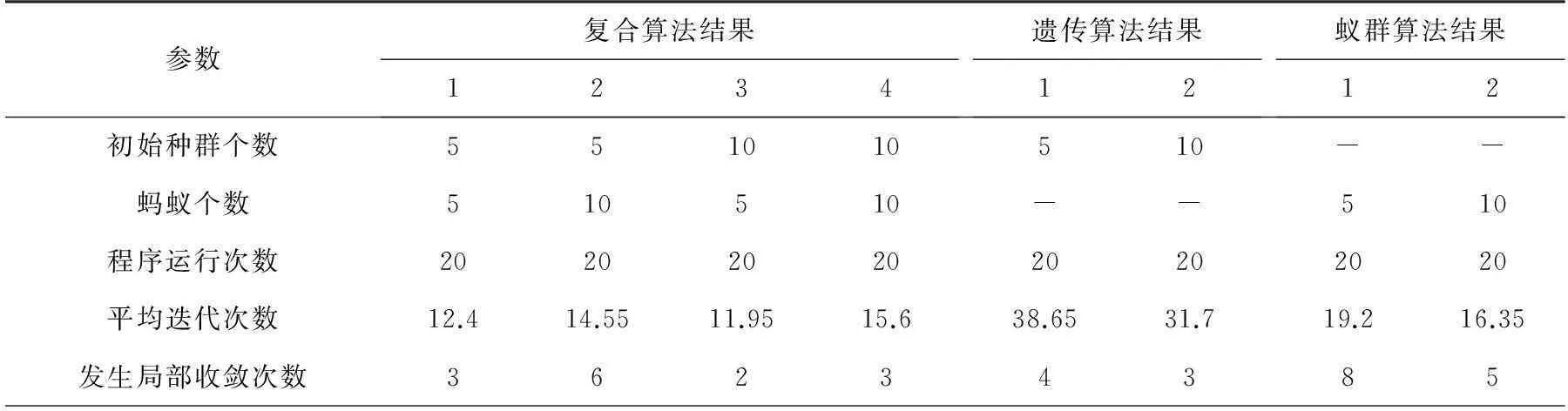
表1　不同参数下的算法运行结果

由图6和表1可以看出，遗传算法虽然收敛性较为稳定，但其收敛速度较慢，而且初始种群必须为可行序列，初始设置较为复杂，蚁群算法虽然收敛速度较快，但由于其初始信息素累积的盲目性，造成收敛不稳定的现象，很容易局部收敛，该复合算法既改进了遗传算法收敛较慢的缺点，又避免了蚁群算法收敛不稳定的缺点。

5结语

提出了一种新的复合算法来解决装配序列规划问题，此算法由多色集合形式化推理算法、遗传算法、蚁群算法融合而成，有效避免了遗传算法对初始种群依赖性强以及蚁群算法容易局部收敛的问题。通过实验验证,复合算法不仅能够有效地生成装配序列，而且具有更好的收敛效率和全局收敛性。

参考文献/References:

[1]彭琛, 刘克能, 周长省. 机械产品装配序列规划研究[J]. 南京师范大学学报(工程技术版), 2006,6(2):81-85.

PENG Chen, LIU Keneng, ZHOU Changsheng. Study on mechanical product’s assembly sequence planning[J]. Journal of Nanjing Normal University (Engineering and Technology), 2006,6(2):81-85.

[2]李原, 张开富, 王挺, 等. 基于遗传算法的飞机装配序列规划优化方法[J]. 计算机集成制造系统, 2006,12(2):188-191.

LI Yuan, ZHANG Kaifu, WANG Ting, et al. Assembly sequence planning optimization for aircraft assembly based on GA[J]. Computer Integrated Manufacturing Systems, 2006,12(2):188-191.

[3]韩晓东, 蔡勇, 蒋刚. 基于改进的遗传算法的装配序列规划[J]. 机械设计与制造, 2009(3):212-214.

HAN Xiaodong, CAI Yong, JIANG Gang. Assembly sequence planning based on the improved genetic algorithm[J]. Machinery Design & Manufacture, 2009(3):212-214.

[4]蒋超, 吴波, 李明宇, 等. 基于遗传算法的产品装配序列规划研究[J]. 机械与电子, 2012(4):7-11.

JIANG Chao, WU Bo, LI Mingyu, et al. Product assembly sequence planning method based on genetic algorithm[J]. Machinery & Electronics, 2012(4):7-11.

[5]丁慧敏, 李蓓智, 周亚琴. 基于遗传算法的装配序列规划[J]. 东华大学学报(自然科学版), 2001,27(6):10-13.

DING Huimin, LI Beizhi, ZHOU Yaqin. Assembly sequence planning based on genetic algorithm[J]. Journal of Donghua University(Natural Science), 2001,27(6):10-13.

[6]陈颖悦, 吴豪杰. 基于改进遗传算法的拆卸序列优化研究[J]. 厦门理工学院学报, 2014,22(5):72-77.

CHEN Yingyue, WU Haojie. Disassembly sequence optimization based on the improved genetic algorithm[J]. Journal of Xiamen University of Technology, 2014,22(5):72-77.

[7]史士财, 李荣, 付宜利, 等. 基于改进蚁群算法的装配序列规划[J]. 计算机集成制造系统, 2010,16(6):1189-1194.

SHI Shicai, LI Rong, FU Yili, et al. Assembly sequence planning based on improved ant colony algorithm[J]. Computer Integrated Manufacturing Systems, 2010,16(6):1189-1194.

[8]邓明星, 唐秋华, 雷喆. 基于蚁群算法的改进装配序列规划方法[J]. 武汉大学学报(工学版), 2013,46(2):246-251.

DENG Mingxing, TANG Qiuhua, LEI Zhe. A novel approach for assembly sequence planning based on ant colony algorithm[J]. Engineering Journal of Wuhan University, 2013,46(2):246-251.

[9]方建新. 基于蚁群算法的装配序列规划研究[D]. 武汉：华中科技大学, 2007.

FANG Jianxin. Research on Assembly Sequence Planning based on Ant Colony Algorithm[D]. Wuhan: Huazhong University of Science & Technology, 2007.

[10]谢龙, 付宜利, 马玉林. 基于蚁群算法的装配序列生成策略[J]. 哈尔滨工业大学学报, 2006,38(2): 180-183.

XIE Long, FU Yili, MA Yulin. Ant-colony-optimization strategy for assembly sequence planning[J]. Journal of Harbin Institute of Technology, 2006,38(2): 180-183.

[11]卢天宇. 遗传蚁群混合算法研究及应用[D]. 西安：西安科技大学, 2012.

LU Tianyu. Research and Application of Genetic Ant Colony Hybrid Algorithm[D]. Xi’an: Xi’an University of Science and Technology, 2012.

[12]赵义武, 牛庆银, 王宪成. 遗传算法与蚁群算法的融合研究[J]. 科学技术与工程, 2010,10(16):4017-4020.

ZHAO Yiwu, NIU Qingyin, WANG Xiancheng. Study on the combination of genetic algorithm and ant algorithm[J]. Science Technology and Engineering, 2010,10(16):4017-4020.

[13]李宗斌, 高新勤, 赵丽萍. 基于多色集合理论的信息建模与优化技术[M]. 北京:科学出版社, 2010.

[14]赵姗姗, 李宗斌. 基于多色集合的装配序列形式化推理方法[J]. 计算机集成制造系统, 2008,14(8):1579-1585.

ZHAO Shanshan, LI Zongbin. Formalization reasoning method for assembly sequences based on polychromatic sets[J]. Computer Integrated Manufacturing Systems, 2008,14(8):1579-1585.

[15]李宗斌. 先进制造中多色集合理论的研究及应用[M]. 北京:中国水利水电出版社, 2005.

[16]王松, 孙振忠, 郭建文, 等. 基于混合蛙跳算法的复杂产品装配序列规划[J]. 计算机集成制造系统, 2014,20(12):2991-2999.

WANG Song, SUN Zhenzhong, GUO Jianwen, et al. Assembly sequence planning based on shuffled frog leaping algorithm[J]. Computer Integrated Manufacturing Systems, 2014,20(12):2991-2999.

[17]于宏, 王成恩, 于嘉鹏, 等. 基于粒子群算法的复杂产品装配序列规划[J]. 东北大学学报(自然科学版), 2010,31(2):261-264.

YU Hong, WANG Cheng’en, YU Jiapeng, et al. Assembly sequence planning based on particle swarm optimization algorithm for complex product[J]. Journal of Northeastern University (Natural Science), 2010,31(2):261-264.

[18]张秀芬, 张树有. 基于粒子群算法的产品拆卸序列规划方法[J]. 计算机集成制造系统, 2009,15(3):508-514.

ZHANG Xiufen, ZHANG Shuyou. Product disassembly sequence planning based on particle swarm optimization algorithm[J]. Computer Integrated Manufacturing Systems, 2009,15(3):508-514.

[19]陈海彬, 郭建文, 孙振忠, 等. 基于自适应变异粒子群优化算法的产品装配序列规划[J]. 组合机床与自动化加工技术, 2015(7):153-156.

CHEN Haibin, GUO Jianwen, SUN Zhenzhong, et al. Product assembly sequences planning based on adaptive particle swarm optimization algorithm with mutation[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2015(7):153-156.

[20]张博, 张洪涛, 赵姗姗, 等. 基于多色集合理论的产品装配规划建模与算法研究[J]. 西安交通大学学报, 2005,39(11):1254-1258.

ZHANG Bo, ZHANG Hongtao, ZHAO Shanshan, et al. Product assembly planning modeling and algorithm based on polychromatic sets[J]. Journal of Xi’an Jiaotong University, 2005,39(11):1254-1258.

An assembly sequence planning method based on composite algorithm

LIU Enfu， LIU Bo， LIU Xiaoyang， LI Yi

(School of Mechanical Engineering, Hebei University of Science and Technology, Shijiazhuang, Hebei 050018, China)

Abstract:To solve the combination explosion problem and the blind searching problem in assembly sequence planning of complex products, an assembly sequence planning method based on composite algorithm is proposed. In the composite algorithm, a sufficient number of feasible assembly sequences are generated using formalization reasoning algorithm as the initial population of genetic algorithm. Then fuzzy knowledge of assembly is integrated into the planning process of genetic algorithm and ant algorithm to get the accurate solution. At last, an example is conducted to verify the feasibility of composite algorithm.

Keywords:computer aided manufacturing; assembly sequence planning; composite algorithm; polychromatic sets; genetic algorithm; ant algorithm

作者简介：刘恩福(1960—)，男，河北石家庄人，教授，主要从事制造业信息化方面的研究。

基金项目：河北省应用基础研究计划重点基础研究项目(14961811D)

收稿日期：2015-09-11；修回日期：2015-11-23；责任编辑：冯民

中图分类号：TP391

文献标志码：A

doi:10.7535/hbkd.2016yx01009

文章编号：1008-1542(2016)01-0052-06