一种面向低频隔振的两自由度球面并联机构

张晓伟，段学超，冷国俊，保　宏

(1.西安电子科技大学电子装备结构设计教育部重点实验室，陕西西安　710071；2.中国电子科技集团公司第二十九研究所，四川成都　610036)



一种面向低频隔振的两自由度球面并联机构

张晓伟1，段学超1，冷国俊2，保宏1

(1.西安电子科技大学电子装备结构设计教育部重点实验室，陕西西安710071；2.中国电子科技集团公司第二十九研究所，四川成都610036)

摘要：针对两转动自由度低频隔振的需求，基于球面并联机构理论提出了一种两转动自由度球面并联隔振装置。从机构学的角度对其进行了工作原理分析和自由度计算，并完成了隔振平台的虚拟样机设计。采用连杆参数的D-H表示法，以连杆圆弧张角为约束条件建立了机构的约束方程，实现了其运动学逆解，并基于数值方法给出了运动学正解的求解过程及正逆解算例。分析和仿真结果表明：所设计的两自由度球面并联机构可操控性强、运动学模型合理有效，能够满足隔振平台所需的低频隔振性能需求。

关键词：机械原理与机构学；隔振平台；球面并联机构；雅可比矩阵；运动学

张晓伟，段学超，冷国俊，等.一种面向低频隔振的两自由度球面并联机构[J].河北科技大学学报,2016,37(1):13-19.

ZHANG Xiaowei, DUAN Xuechao, LENG Guojun, et al.A two-degree-of-freedom spherical parallel mechanism with low-frequency vibration isolation[J].Journal of Hebei University of Science and Technology,2016,37(1):13-19.

主动隔振技术作为振动控制领域的一个重要分支，具有自适应性好、可对低频振动进行隔离等优点，因而成为隔振技术的研究热点[1-2]。从隔振原理上讲，主动隔振是在被控系统中引入次级振源，并通过一定的控制方法调节次级振源的输出，使其产生的振动与主振源(干扰)的振动相抵消,从而达到隔振的目的[1]。从系统的功能看，隔振稳定平台的机械机构是主动隔振系统的重要组成部分，合理的机械机构是稳定平台实现其功能、提高稳定精度的前提。稳定平台最初是串联型机构较多。1965年STEWART提出著名的六自由度并联式平台[3-4]，从此开始了基于Stewart并联机构的研究，目前平台可以实现6个自由度的稳定。而对于常见的少自由度的稳定平台，按照机构形式可以分为2类：一类是框架机构[5-6]，另一类为多点支撑式结构[7]。相对于这2种结构形式，并联机构具有承载能力高、刚度大、结构简单稳定、精度高、易实现高速运动、求解运动学逆解容易等优点[8]，从而使平台具备更好的稳定性。

从机构学的角度看，机器人可分为球面机器人、平面机器人和空间机器人[9]，其中球面机器人是一特殊类型的机构，它是联系平面机构与空间机构的桥梁。当球面机构运动时，其构件上所有点在一个球面上运动。除具有并联机器人的一般特性外，球面机构还具有结构简单、工作空间大、不易发生干涉、运动学计算简单、控制容易等优点[10]。随着机器人技术的发展，各种形式的球面并联机构也引起了人们的研究兴趣，并在工程中得到了成功应用[11-13]。本文提出了一种应用于移动载体上的两自由度主动隔振平台机构模型，通过隔振可减小载体由于位姿变换、干扰振动以及发动机振动等对所隔振设备的影响，使其具有一个高品质的工作环境。

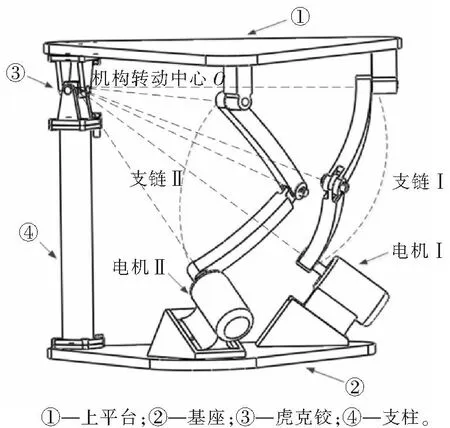
图1　两转动自由度球面并联机构的原理图Fig.1　Schematic of the two-degree-of-freedom spherical parallel mechanism

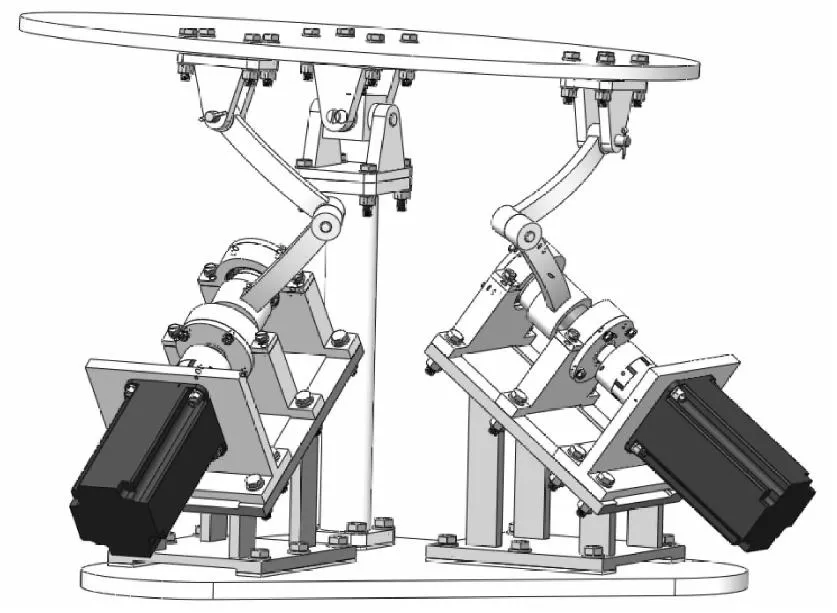
图2　两转动自由度球面并联机构的虚拟样机Fig.2　Virtual prototype of the two-degree-of-freedom spherical parallel mechanism

1机构组成与运动原理

1.1　机构简介

所设计的两转动自由度球面并联机构的原理图见图1，机构分为上平台①和基座②，上平台作为设备的承载体具有两转动自由度。上平台与基座间由2个支链和1个支柱④连接，支链所有运动副都为转动副。支柱下端与基座固连，上端通过虎克铰③与上平台相连。机构符合球面机构的一般特性[14-15]，在运动过程中支链连杆上的所有点均在以某一定点为球心的球面上运动，并且所有转动副及电机轴轴线皆交汇于该定点，该定点叫做机构的运动中心。

根据所设计机构的特性，选择虎克铰中心旋转体的型心作为机构的转动中心。根据机构原理，结合机械设计相关知识，该机构的实际设计虚拟样机如图2所示。

1.2　自由度计算

由机构学知识可知，修正后的Kutzbach-Grubler自由度计算公式为[16]

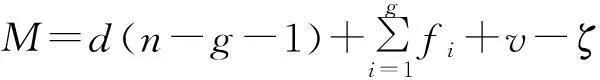
(1)

式中：M为机构的自由度数目；n为机构中构件的数目；g为机构中运动副的数目；fi为第i个运动副的自由度数；d为机构的阶数；v为机构中冗余约束的数目；ζ为机构中局部自由度的数目。

因为平面机构或球面机构的公共约束为3[17]，则该机构作为球面机构具有3个公共约束[6]，即d=3，其他参数n=6，g=7。由于与支链相关的运动副都为单自由度的转动副，所以对于这些运动副都有fi=1(i=1，2，…，6)。由于支柱与上平台是由虎克铰连接，故有2个自由度，所以有f7=2。从机构的机构形式可以看出，机构冗余数目v=0，机构局部自由度数目ζ=0。将上述参数代入式(1)有

M=3×(6-7-1)+6×1+2-0=2 。

所以该球面并联机构的自由度数目为M=2，并且通过分析可知机构具有沿2个方向转动的自由度。驱动位置选在支链与下平台连接的转动副处，这样在机构运动过程中两驱动电机带动支链运动，支链就可以带动上平台在自由度方向上完成位姿的变换。

2机构运动学分析

2.1　坐标系的建立

按照连杆参数的D-H表示法建立坐标系：O-X0Y0Z0，O-XYZ和O-XijYijZij(ij表示第i个分支的第j个转动副，以下i，j的取值都为1或2)，如图3所示。由于两自由度球面并联机构各个连杆系都是绕着球心转动，因此选取球心O作为各坐标系的原点；支柱轴线作为固定坐标系的Z0轴，指向上平台的方向为正方向；各连杆坐标系的Zij分别为第i个分支的第j个转动副的轴线方向，方向指向球外；固定坐标系的X0轴是Z0轴和Z11轴所张成平面的法线；连杆坐标系的Xij轴分别为Zij与Zi，j+1所张成平面的法线方向；将过球心O且垂直于上平台的垂线作为动坐标系的Z轴；X轴的方向为Z13与Z轴所张成平面的法线方向(与X13轴重合)；各坐标系的Y轴分别由右手定则确定。

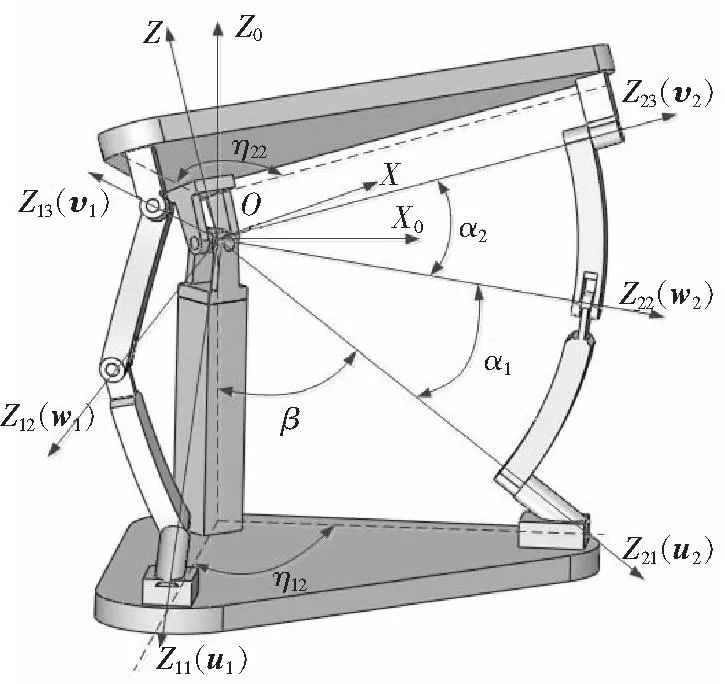
图3　各坐标系的建立Fig.3　Coordinates of the system

该机构的结构参数有α1，α2，β，η1i，η2i。其中η1i(i=1,2)分别为各分支的Zi1在基座的投影与第一分支的Z11投影所成的角度；η2i(i=1,2)分别为各分支的Zi3在上平台的投影与第一分支的Z13投影所成的角度。

2.2　运动学逆解的推导

应用连杆参数的D-H表示法[18]及球面解析理论[19]都可以进行机构运动学逆解的推导，此处以连杆参数的D-H表示法为例进行运动学逆解推导。由于机构的上平台只有2个转动的自由度，记上平台位姿为横滚角φx、俯仰角φy，则上平台位姿可表示为

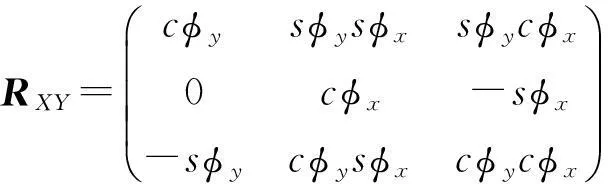
(2)

式中：c表示cos函数运算，s表示sin函数运算，下同。

2.2.1矢量ui，wi和vi的方向余弦

定义如下各单位向量：ui沿Zi1方向，wi沿Zi2方向，vi沿Zi3方向，以上i=1,2。

通过连杆参数的D-H表示法进行坐标旋转变换可得固定坐标系O-X0Y0Z0和O-Xi2Yi2Zi2之间的转换矩阵为

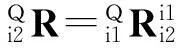
其中

(3)

因此，可得

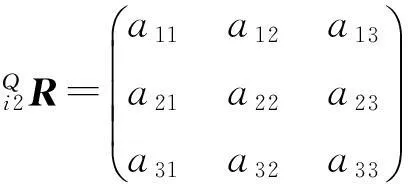
(4)

式中：

a11=cθi2cη1icθi1+cθi2sη1icβsθi1-cα1sθi2cη1isθi1+cα1sθi2sη1icβcθi1-sη1isβsα1sθi2,

a12=-sθi2cη1icθi1-sθi2sη1icβsθi1-cα1cθi2cη1isθi1+cα1cθi2sη1icβcθi1-sη1isβsα1cθi2,

a13=-sα1cη1isθi1+sα1sη1icβcθi1+sη1isβcα1,

a21=cθi2sη1icθi1-cθi2cη1icβsθi1-cα1sθi2sη1isθi1-cα1sθi2cη1icβcθi1+cη1isβsα1sθi2,

a22=-sθi2sη1icθi1+sθi2cη1icβsθi1-cα1cθi2sη1isθi1-cα1cθi2cη1icβcθi1+cη1isβsα1cθi2,

a23=-sα1sη1isθi1-sα1cη1icβcθi1-cα1cη1isβ,

a31=sβsθi1cθi2+sβcθi1cα1sθi2+cβsα1sθi2，

a32=-sβsθi1sθi2+sβcθi1cα1cθi2+cβsα1cθi2,

a33=sβcθi1sα1-cβcα1。

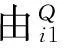
ui=[sη1isβ-cη1isβ-cβ]T，

(5)

同理，根据上平台位姿矩阵(2)，结合坐标的旋转变换可得到vi的表达式：

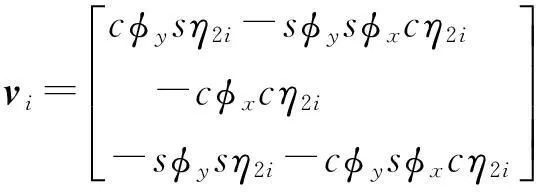
(6)

2.2.2由机构约束条件导出位姿逆解

各分支中间转动副wi与相应上平台转动副vi以上连杆α2相连，就有约束方程

wi·vi=cα2,i=1,2。

(7)

将式(5)和式(6)代入式(7)并整理可得

Aisθi1+Bicθi1+Ci=0,i=1,2，

式中：

Ai=-sα1cη1ivix-sα1sη1iviy,

Bi=sα1sη1icβvix-sα1cη1icβviy+sβsα1viz,

Ci=sη1isβcα1vix-cη1isβcα1viy-cβcα1viz-cα2。

解得

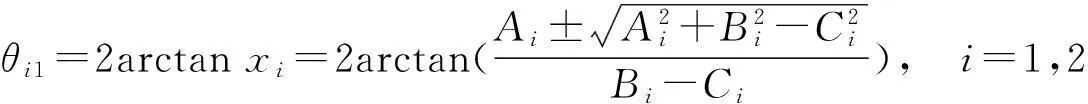
(8)

式(8)表明，已知动平台的位姿，便可求输入角θ11和θ21，并且由式(8)可以看出，每个输出位姿对应2组输入解，根据机构的运动特性易确定符合约束关系的合理解。

2.2.3逆解算例

球面并联机构的各设计参数分别为α1=25°,α2=30°,β=53.13°,η11=0°,η12=90°,η21=0°,η22=90°。规划动平台运动轨迹为与动平台固连的动坐标系Z轴绕固定坐标系的Z0轴做锥角为30°的圆锥面匀速运动，如图4所示。图中圆形轨迹为动平台单位法线(与Z轴重合)端点在运动过程中所走过的轨迹，该点也作为动平台的标记点。

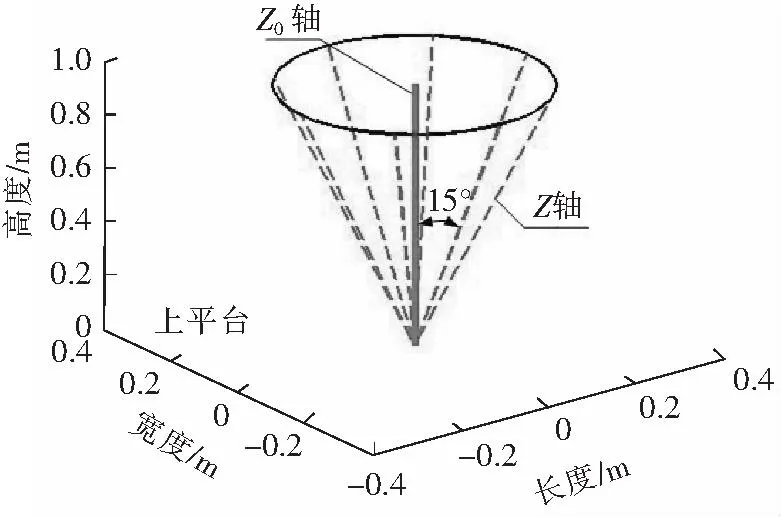
图4　圆锥面轨迹规划Fig.4　Motion planning of the cone trajectory

根据以上所述的机构运动学逆解过程，对所规划的姿态轨迹进行运动学逆解求解。图5所示为通过逆解算法得到的2个驱动电机的角位移输入曲线。

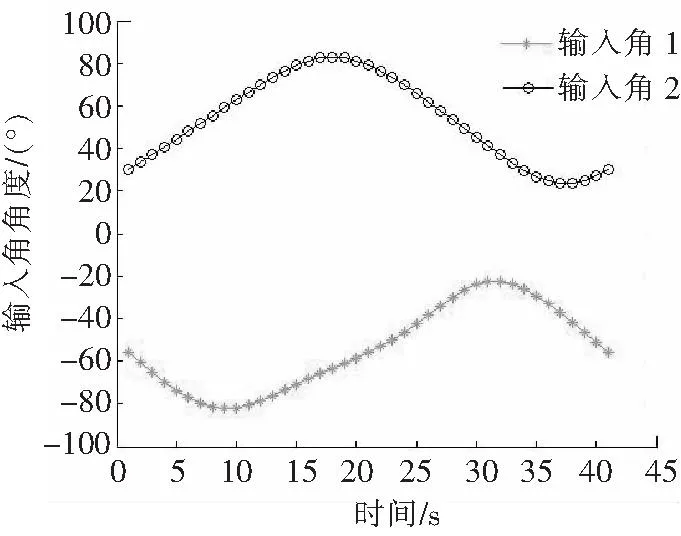
图5　圆锥面轨迹规划输入曲线Fig.5　Input angle curves for the cone trajectory

2.3　运动学正解的推导

2.3.1雅克比矩阵求解

将运动学位姿反解的约束方程(7)中的输入角和输出角位移均看成时间t的函数，等式两边同时对时间t求导，得：

(9)

用矢量形式将式(9)表示为

Aθ′+Bφ′=0 ，

(10)

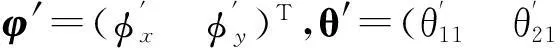
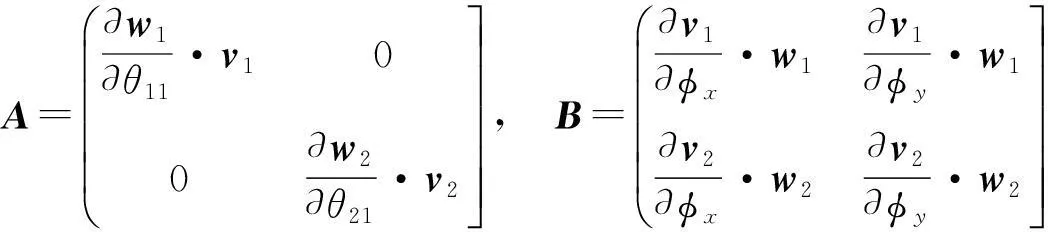
对式(10)进行整理得

φ′=Jθ′,

(11)

其中

J=-B-1A,

(12)

则J即为输入角速度矢量θ′向输出角转速矢量φ′线性变换的雅克比矩阵。

2.3.2由数值形式给出机构位姿正解

并联机构位姿正解是机构学研究的一个重要课题，是研究机构运动学、动力学和轨迹控制等方面的基础。与串联机器人相比，并联机构反解容易，但正解需要求解一组非线性方程组，难度较大。国内外学者采用不同的方法对正解进行了研究[20-22]，本文用一种常用的最速下降法对机构进行位置正解求解。

由于动平台在其工作空间内运动，假定它从任一已知的初始位姿P0经过控制作用后，达到当前位姿Pd，此时各分支输入角位置矢量为θd。在实际过程中P0靠标定来确定，θd则是由分支伺服电机的编码器读数值换算得出。位姿正解算法的根本任务是根据P0，θd求解出上平台位姿Pd。

位姿正解的迭代算法如下：

1)已知上平台初始位姿P0，分支输入角位置矢量θd，给定算法的收敛精度ε>0，令k=0；

2)通过运动学逆解体系计算初始位姿下输入角位置状态：θk=InvKin(Pk)，得Δθk=θd-θk；

3)计算Sk=-J-1(θk)Δθk，若‖Sk‖≤ε，则停，Pd=Pk，否则转4)；

4)Pk+1=Pk+Sk，k=k+1，转2)。

由上述数值迭代过程即可获得机构的位置正解。

2.3.3正解算例

应用2.2.3中的机构参数和位姿逆解结果，将逆解所得的驱动电机输入数据做机构位姿的正向求解。图6所示为所述位姿正解算法所得的动平台横滚角(Rollx)和俯仰角(Pitchy)的输出曲线；图7表示由正解输出数据得到的动平台标记点所走的轨迹与原规划轨迹的对比图。虚线表示上节中规划的动平台运动轨迹，星号点线代表通过正解算法获得的动平台运动轨迹，2组轨迹完全吻合，验证了本文提出机构的运动学正逆解算法的正确性和有效性。

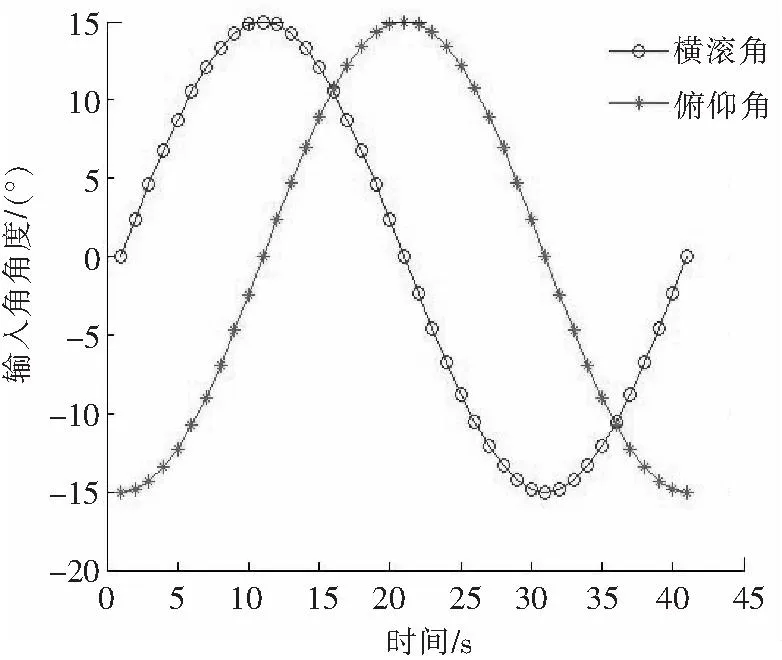
图6　正解输出曲线Fig.6　Output curve of the forward kinematics

图7　正解输出轨迹与原规划轨迹的对比图Fig.7　Comparison between the solutions of forward kinematics and original planned trajectory

3结语

本文分析了两自由度球面并联机构的工作原理，进行了自由度分析和虚拟样机的设计。分别以解析形式和数值形式给出了机构运动学正、逆解结果，并且通过仿真验证了所提出正、逆解算法的一致性。分析表明：本机构可操控性强，所建立的运动学模型合理有效，基于运动学方程进行合理的控制，本机构可以在基体与设备中间实现振动抵消、补偿的作用，达到主动隔振的目的。此外，根据不同的工程应用背景，可以针对本文所提出的两自由度球面并联平台进行不同的参数设定，以满足不同场合的应用需求。

参考文献/References：

[1]张磊, 付永领, 刘永光, 等. 主动隔振技术及其应用与发展[J]. 机床与液压, 2005 (2): 5-8.

ZHANG Lei, FU Yongling, LIU Yongguang, et al. Active vibration isolation and its application and development[J]. Machine Tool & Hydraulics, 2005(2):5-8.

[2]张春红, 汤炳新. 主动隔振技术的回顾与展望[J]. 河海大学常州分校学报, 2002, 16(2): 1-5.

ZHANG Chunhong, TANG Bingxin. The retrospection and prospection of active vibration isolaion technique[J].Journal of Hohai University Changzhou, 2002, 16(2): 1-5.

[3]STEWART D.A platform with six degrees of freedom[J]. Proceedings of the Institution of Mechanical Engineer, 1965, 180: 371-386.

[4]HUNT K H. Kinematic Geometry of Mechanisms[M]. Oxford: Clarendon Press, 1978.

[5]王昭. 某天线稳定平台的结构设计[J]. 电子机械工程, 2012, 28(4): 25-28.

WANG Zhao. Structure design of an antenna stabilizing platform[J]. Electro-Mechanical Engineering, 2012, 28(4): 25-28.

[6]张鹏. 舰载摄像稳定平台的结构设计[J]. 舰船电子对抗, 2006, 29(3): 70-73.

ZHANG Peng. Structural design of shipboard shooting stabilized platform[J]. Shipboard Electronic Countermeasure, 2006, 29(3): 70-73.

[7]邹慧君, 高峰. 现代机构学进展[M]. 北京: 高等教育出版社, 2007.

[8]黄真, 孔令富. 并联机器人机构学理论及控制[M]. 北京: 机械工业出版社, 1997.

[9]丛爽, 尚伟伟. 并联机器人建模、控制优化与应用[M]. 北京: 电子工业出版社，2010.

[10]刘艳芳, 杨随先. 球面机构研究动向[J]. 机械设计与研究, 2010, 27(1): 32-35.

LIU Yanfang, YANG Suixian. Advances and trends in spherical mechanisms research[J]. Machine Design and Research, 2010, 27(1): 32-35.

[11]GWINNETT J E. Amusement Devices[P]. US Patent:1,789,680,1931-01-20.

[12]方中甲. 面向颈关节的三自由度球面并联机构的研究[D]. 哈尔滨:哈尔滨工业大学,2004.

FANG Zhongjia. Research on Three DOF Spherical Parallel Mechanism for The Neck Joint[D].Harbin:Harbin Institute of Technology, 2004.

[13]周玉林, 高峰. 具有偏置输出的3自由度球面并联仿生肩关节[P]. 中国专利：ZL200810055021.8, 2008-11-12.

[14]GOSSELIN C M,HUMEL J F.The agile eye:A high-performance three-degree-of-freedom camera-orienting device[C]//IEEE International Conference on Robotics and Automation.[S.l.]:[s.n.],1994:781-786.

[15]GOSSELIN C M, ST-PIERRE E, GAGNE M.On the development of the agile eye[J]. IEEE Robotics & Automation Magazine, 1996, 3(4): 29-37.

[16]HUANG Zhen. The kinematics and type synthesis of lower-mobility parallel manipulators[C]//Proceedings of the 11th Word Congress in Mechanism and Machine Science.Tianjin:[s.n.],2004:65-76.

[17]黄真, 刘婧芳, 李艳文. 论机构自由度[M]. 北京: 科学出版社, 2011.

[18]战丽娜. 基于球面机构的肩关节的分析与设计[D].秦皇岛:燕山大学,2005.

ZHAN Lina. The Analysis and Design of a Shoulder Joint Based on Spherical Manipulator[D].Qinhuangdao:Yanshan University, 2005.

[19]黄真. 空间机构学[M]. 北京:机械工业出版社, 1989.

[20]INNOCENTI C, PARENTI-CASTELLI V. A novel numerical approach to the closure of the 6-6 Stewart platform mechanism[C]//International Conference on Advanced Robotics, Robots in Unstructured Environments, 91 ICAR.[S.l.]:IEEE, 1991:851-855.

[21]曲义远, 黄真. 空间六自由度多回路机构位置的三维搜索方法[J]. 机器人, 1989, 3(5): 25-29.

QU Yiyuan, HUANG Zhen. Three-dimensional search method of a six DOF multi-loop mechanism[J]. Robot, 1989, 3(5): 25-29.

[22]李树军, 王阴, 王晓光. 3-RPS并联机器人机构位置正解的杆长逼近法[J]. 东北大学学报, 2001, 22(6): 285-287.

LI Shujun, WANG Yin, WANG Xiaoguang. Forward position analysis of 3-RPS in-parallel manipulator using self-modified successive approximation method[J]. Journal of Northeastern University, 2001, 22(6): 285-287.

A two-degree-of-freedom spherical parallel mechanism with low-frequency vibration isolation

ZHANG Xiaowei1, DUAN Xuechao1, LENG Guojun2, BAO Hong1

(1. Key Laboratory of Electronic Equipment Structure Design of Ministry of Education, Xidian University, Xi’an, Shaanxi 710071, China; 2. Southwest China Research Institute of Electronic Equipment, Chengdu, Sichuan 610036, China)

Abstract:Aiming at the requirements of the vibration isolation with two rotational degrees of freedom under specific conditions, a spherical 2-DOF parallel vibration isolation platform is proposed based on the theory of spherical parallel mechanism. From the view point of theory of mechanism, the operating principle is analyzed and the degree of freedom is calculated, and the virtual prototype design of vibration isolation platform is carried out. With D-H representation method of robot mechanism, the constraint equation is developed under the constraint conditions of the above link arc angle, and the inverse kinematics is realized. The kinematics positive solution process is given based on numerical method, and the solution examples of positive and inverse solution are given. Analysis and simulation results show that the 2-DOF spherical parallel mechanism proposed in this paper has the characteristics of good controllability, and the kinematic model is reasonable and effective, meeting the need of low-frequency vibration isolation performance.

Keywords:mechanical principle and mechanism theory; vibration isolation platform; spherical parallel mechanism; Jacobian matrix; kinematics

通讯作者：段学超博士。E-mail:xchduan@xidian.edu.cn

作者简介：张晓伟(1988—)，男，河北承德人，硕士研究生，主要从事并联机器人技术方面的研究。

基金项目：国家自然科学基金(51405362，51490660)

收稿日期：2015-07-10；修回日期：2015-09-30；责任编辑：冯民

中图分类号：TD421

文献标志码：A

doi:10.7535/hbkd.2016yx01003

文章编号：1008-1542(2016)01-0013-07