莱维飞行与粒子群的混合搜索算法

牛海帆，宋卫平，宁爱平

(太原科技大学电子信息工程学院，太原 030024)



莱维飞行与粒子群的混合搜索算法

牛海帆，宋卫平，宁爱平

(太原科技大学电子信息工程学院，太原 030024)

摘要：粒子群算法在解决多维的复杂优化问题时，存在收敛精度不高和易陷入局部收敛等不足，针对这些问题，将莱维飞行与偏好随机游动引入粒子群算法中，提出莱维飞行与粒子群的混合搜索算法。在该算法的解更新过程中，采用莱维飞行、偏好随机游动与粒子群算法的更新方程以串行方式对得到的解进行更新寻优。实验结果表明，改进后的混合算法与粒子群算法相比较，加快了收敛速度，提高了搜索精度。

关键词：粒子群优化算法；莱维飞行；函数优化

粒子群算法(PSO)[1-2]是在1995年由Kennedy和Eberhart提出的一种元启发式算法，同遗传算法[3]、蚁群算法[4]、萤火虫算法[5]等类似，是基于群体搜索策略的群智能优化算法。该算法原理简单、参数少，易于编程实现。然而，基本的粒子群算法亦存在缺点：易陷入早熟收敛，解的质量不高等。近年来研究者们仍然一直在努力对算法提出改进，如：李俊吉、崔志华、崔炎在2010年提出了一种空间分割微粒群算法[6]，张英杰、邵岁峰在2011年提出了基于云模型的粒子群算法[7]；Zahra Beheshti，Siti Mariyam Shamsuddin，Siti Sophiayati Yuhaniz在2013年提出了一种二进制加速粒子群算法[8]；G.Giftson Samuel， C.Christober Asir Rajan在2015年提出了将粒子群算法、遗传算法、和蛙跳算法相融合的一种混合算法[9]等。每种改进算法都在不同程度上提高了收敛性能，但仍然存在诸多不足。文献[6]中的算法对低维耦合性的测试函数的寻优能力较差。文献[7]中的算法参数较多，且参数的选择对算法性能的影响还有待进一步证明与研究。文献[8]中的算法局限于解决离散优化问题。文献[9]中的算法结构复杂，不易编程。

莱维飞行[10]是一种随机行走，其飞行间隔服从幂率分布。在智能优化算法中应用莱维飞行，能够扩大搜索范围、增加种群多样性[11]，更加容易跳出局部最优点。在本文中，将莱维飞行搜索方法应用于粒子群算法，正好能够弥补粒子群算法存在的不足。通过对5个基准测试函数的仿真测试，仿真结果表明这种改进算法的收敛性能明显优于基本的粒子群算法。

1PSO算法

在基本PSO中，设有n个粒子构成一个群体，其中第i个粒子的位置由D维向量Xi=(xi1,xi2,…,xiD)来表示，速度用Vi=(vi1,vi2，…,viD)来表示。粒子的初始位置和初始速度是在搜索区域内随机初始化得到的。每个粒子的位置代表一个解，将向量Xi代入目标函数就可以计算出其适应值f1，比较各粒子的适应值，适应值最小的位置即是目前群体的最优位置。在粒子第t+1次迭代中，粒子的位置与速度更新公式如下：

Vg+1,i=ωVg,i+c1r1(Pg,i-Xg,i)+c2r2(Pg-Xg,i)

(1)

Xg+1,i=Xg,i+Vg+1,i

(2)

式中，ω是惯性权重，c1、c2是学习因子；r1、r2是介于(0,1)之间服从均匀分布的随机数；Vg,i和Xg,i分别代表了第g代第i个粒子的速度和位置；Pg+1,i是第i个粒子目前搜索到的最优位置，Pg是整个种群搜索到的历史最优值。

2莱维飞行与粒子群的混合搜索算法

2.1　莱维飞行

莱维飞行随机游动是一种很好的搜索策略，其飞行的步长满足一个重尾的稳定分布。在智能优化算法中采用莱维飞行，能够扩大搜索范围、增加种群多样性，更容易跳出局部收敛。

在粒子群算法中采用莱维飞行对目前的粒子位置Xi进行更新，更新公式为：

Xg+1,i=Xg,i+α⊕Levy(β)

(3)

式中，Xg,i是g代第i个粒子的位置；α是步长因子；⊕是点乘积，Levy(β)为随机搜索路径，Levy(β)表示服从参数为β的莱维分布，即：

Levy(β)~u=t-1-β

(4)

采用式(5)计算莱维随机数[12]：

(5)

其中u，v均服从标准正态分布；β的取值区间一般为1<β<3，在本文中，β=1.5；

(6)

式中Γ是标准的Gamma函数。

由以上式子可知莱维飞行更新位置方程为：

(7)

2.2　偏好随机游动

随机游动在解决定位目标的查找问题时具有很好的能力，所以将其应用在智能优化算法中能够加快找到最优解的速度。在优化算法的解更新过程中，按一定的概率(发现概率)丢弃部分解之后，算法采用偏好随机游动重新生成相同数量的新解，见式(8)：

Xg+1,i=Xg,i+r(Xg,l-Xg,k)

(8)

其中r是(0,1)区间内服从均匀分布的随机数；Xg,l和Xg,k是代表第g代的两个不同的随机解。

2.3　混合算法的步骤

混合算法的基本思想就是将莱维飞行和偏好随机游动引入粒子群算法，弥补粒子群算法收敛精度低、易陷入局部收敛的不足。这种新的搜索算法定名为HPSO.如图1为HPSO算法的流程。

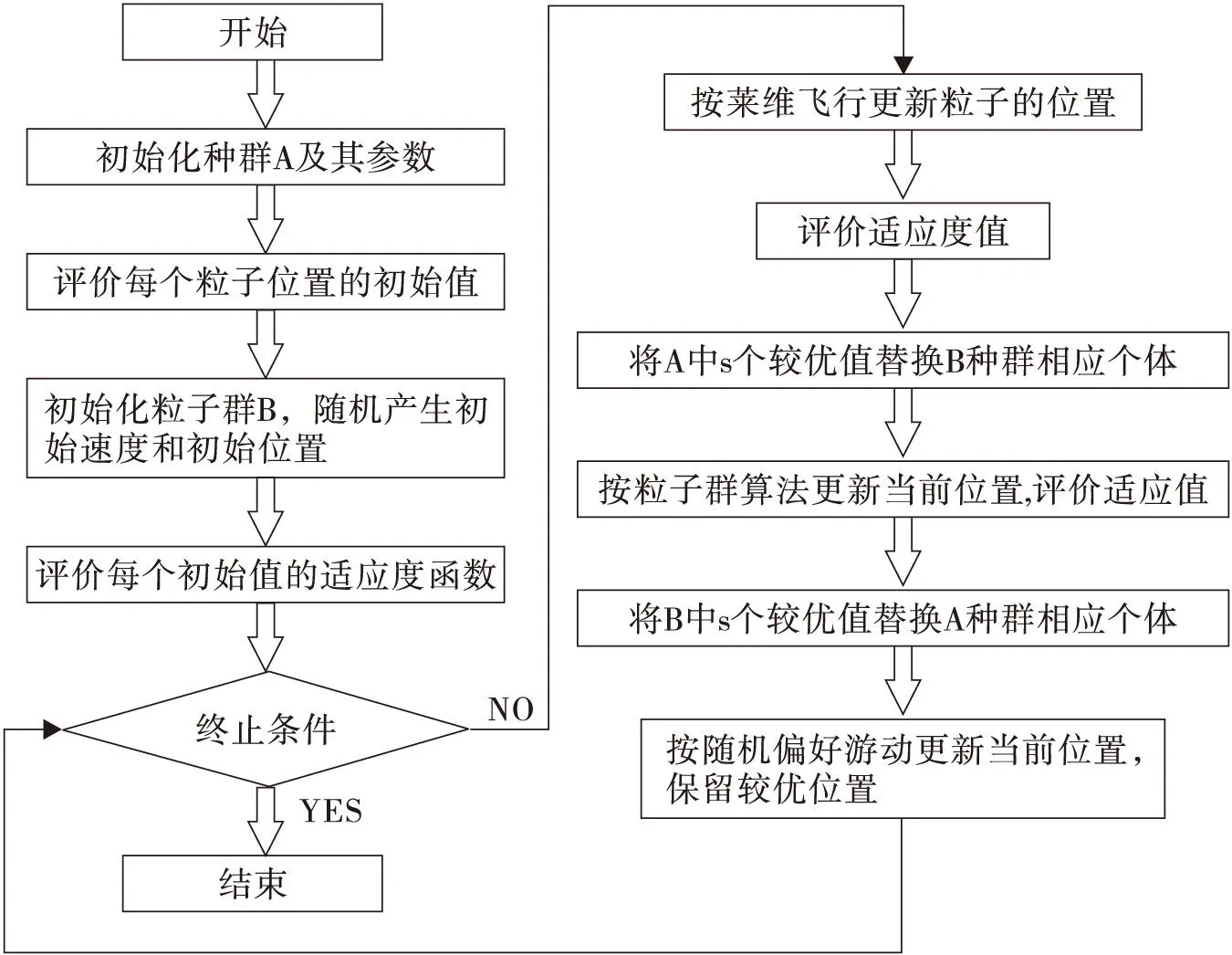
图1　混合粒子群算法流程图

混合算法步骤如下：

步骤1：目标函数f(X)，初始化种群A和B.随机产生n个粒子的初始位置和初始速度，每个粒子的位置代表一个解。搜索空间维数为D，设置粒子群算法的其他基本参数。

步骤2：对A种群根据式(7)更新粒子位置，评价适应度值，将A中的s个较优粒子位置替换掉B中的相应个体。

步骤3：对步骤2更新后的B种群按式(1)和(2)更新粒子速度和位置，比较适应度值，将B中的s个较优粒子位置替换掉A中的相应个体。

步骤4：对步骤3更新后的A种群按随机偏好游动更新式(8)更新当前位置，保留较优位置。

步骤5：判断是否满足结束条件，若达到，则循环结束，否则，返回步骤2.

步骤6：输出全局最优值。

3对函数优化问题的实验研究

3.1　实验设计

为了观察混合算法求解多维优化问题的收敛速度和收敛精度，选择的测试环境为：Windows7，内存4 G，MATLAB7.1.将HPSO应用在5个测试函数中，见表1.f1是简单的单峰函数。f2-f4是多峰函数，其局部极值点随维数的增加而增加。f5在维数为2或3时是复杂的单峰函数，但维数高时可能有多个极值点。

表1　测试函数

实验中参数具体设置为：PSO算法中，种群大小设置为20，惯性权重ωmax=0.9，ωmin=0.4，c1=c2=2.0.在HPSO算法中，参数设置与PSO算法相同，两种算法分别对5个基准测试函数的最小值寻优，分别独立运行50次后取平均值作为最终的测试结果。

3.2　实验结果与分析

3.2.1收敛精度与收敛速度测试

固定最大迭代次数为2 000.实验结果如表2-6和图2-6所示。在表2-6中分别比较了HPSO和PSO算法下的最优值、最差值、平均值、中位数、标准差值。图2-6是函数f1、f2、f3、f4、f5采用HPSO和PSO算法独立运行50次的平均适应度值的进化曲线图。实验结果显示，在优化f2、f3函数时，HPSO虽然后期收敛速度较慢，但仍然比PSO算法具有更好的优化能力。在优化f1、f5函数时，虽然在前期HPSO算法的收敛速度没有PSO算法快，但是HPSO更易跳出局部收敛，得出比PSO算法更优的解。HPSO明显具有较好的收敛精度和较快的收敛速度。在优化f4函数时，虽然两种算法的收敛精度没有明显提高，但HPSO与PSO相比具有更快的收敛速度。结果表明，总体上来说HPSO算法比PSO算法性能更优。

3.2.2固定目标精度的成功率和迭代次数测试

表7为5种基准测试函数在各自固定的目标精度下独立运行50次的成功率和迭代次数，其最大迭代次数设置为2 000.由表7 可以看出，HPSO在已设置的条件下，能够100%的达到目标精度，而PSO的成功率相对较低。同时，HPSO算法达到目标精度的迭代次数明显比PSO算法少。实验结果说明，HPSO算法的优化能力比PSO算法好。

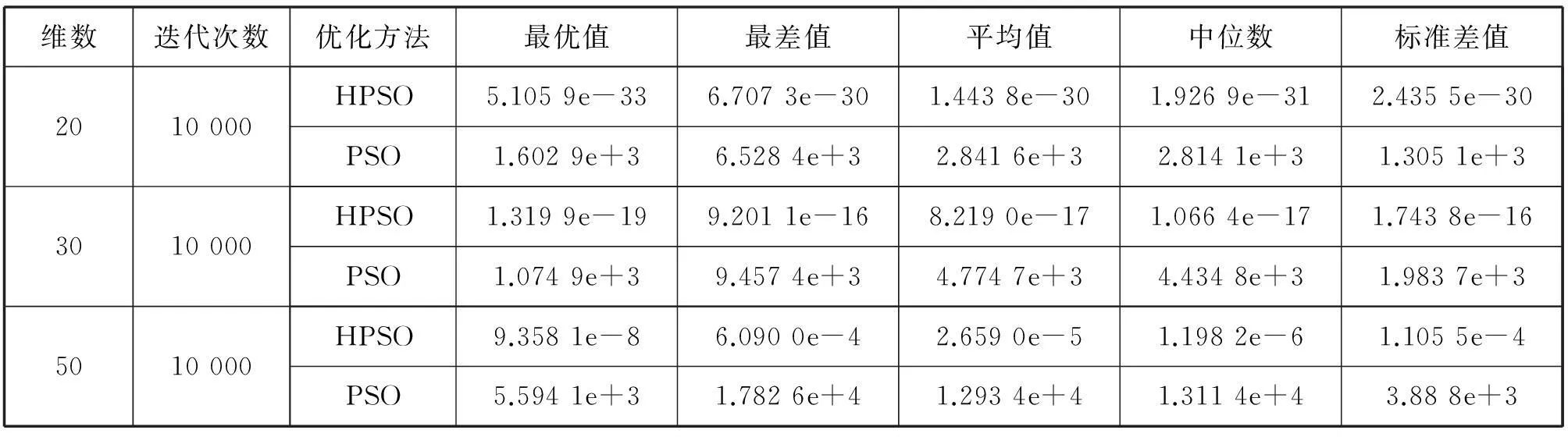
表2　sphere函数实验结果

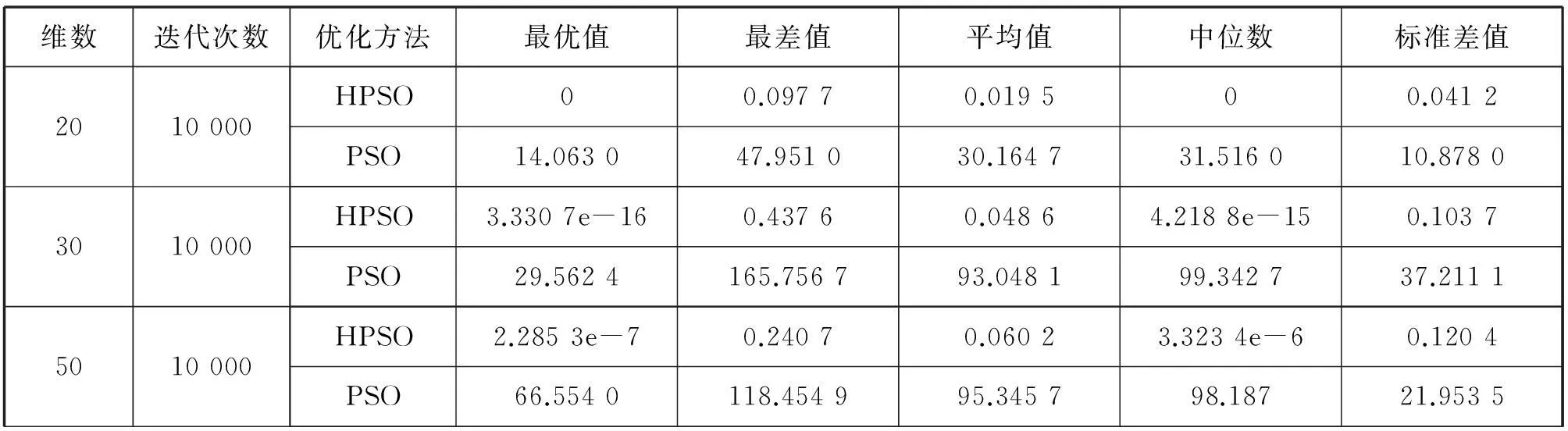
表3　griewank函数实验结果

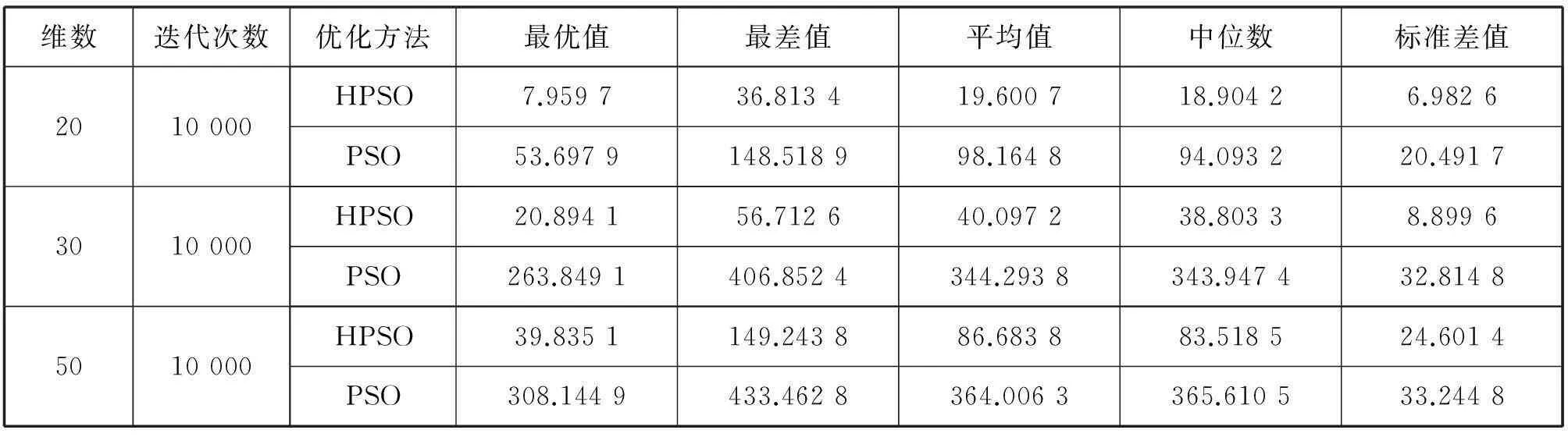
表4　rastrigin函数实验结果

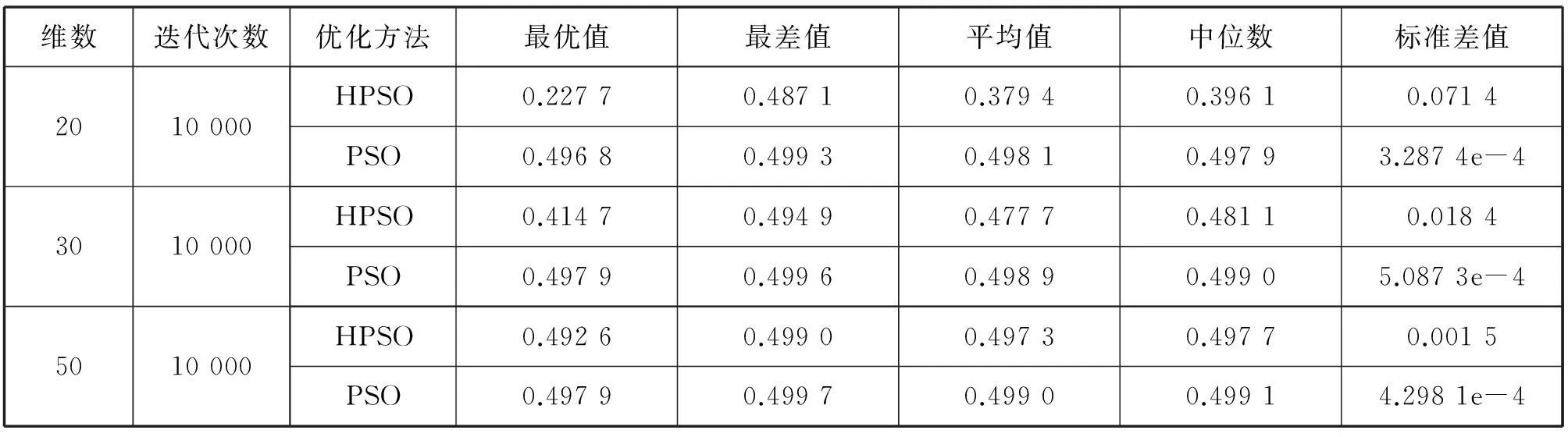
表5　schaffer函数实验结果

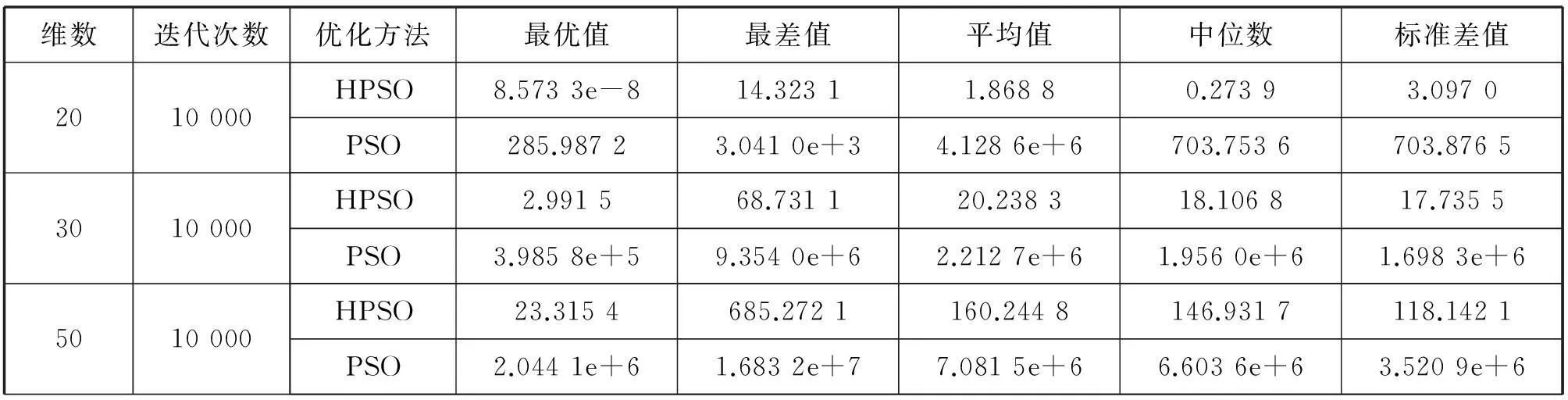
表6　rosenbrock函数实验结果

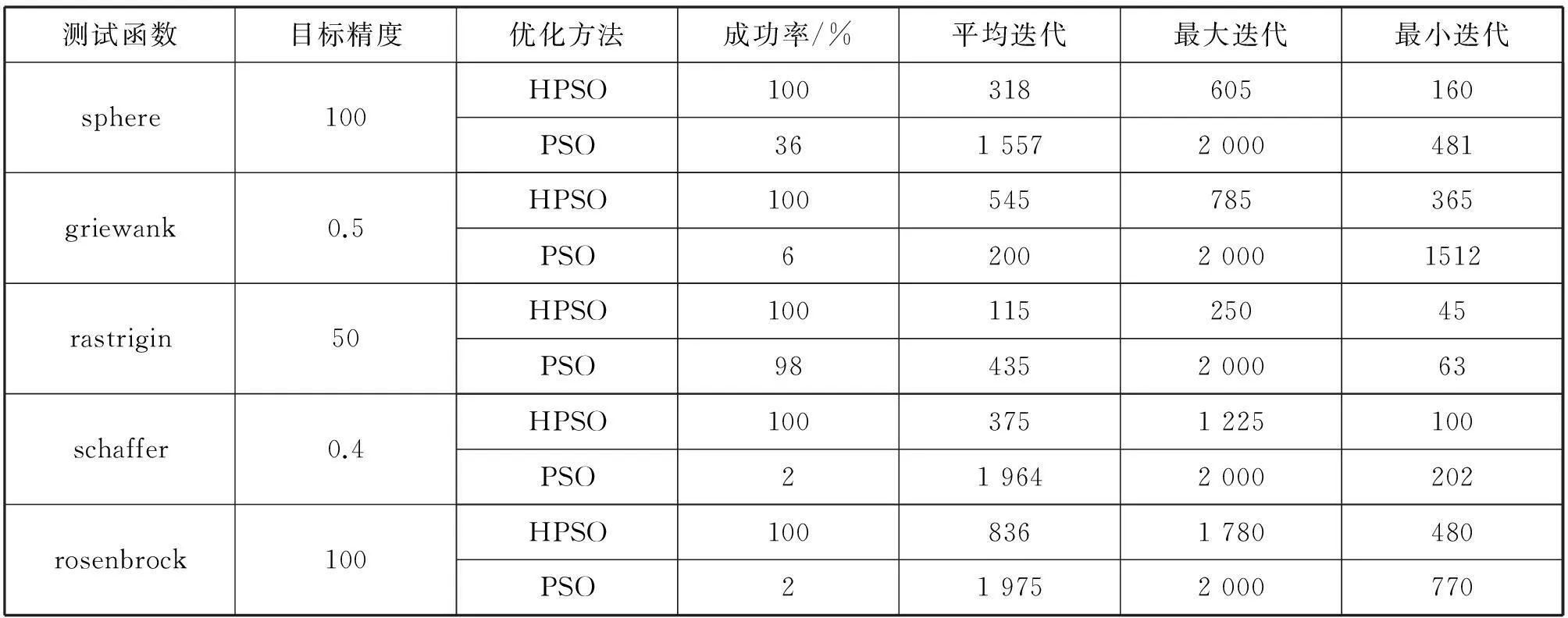
表7　在固定目标精度下的迭代次数

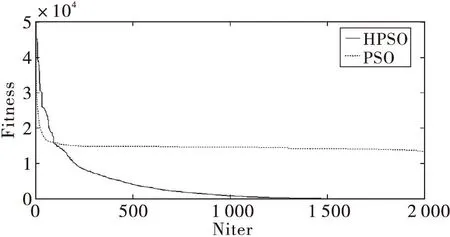
图2　sphere函数在20维下的进化曲线

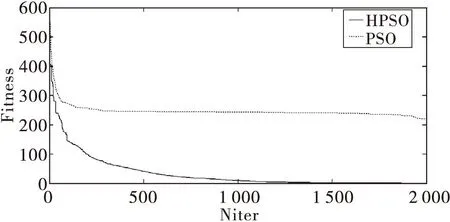
图3　griewank函数在20维下的进化曲线

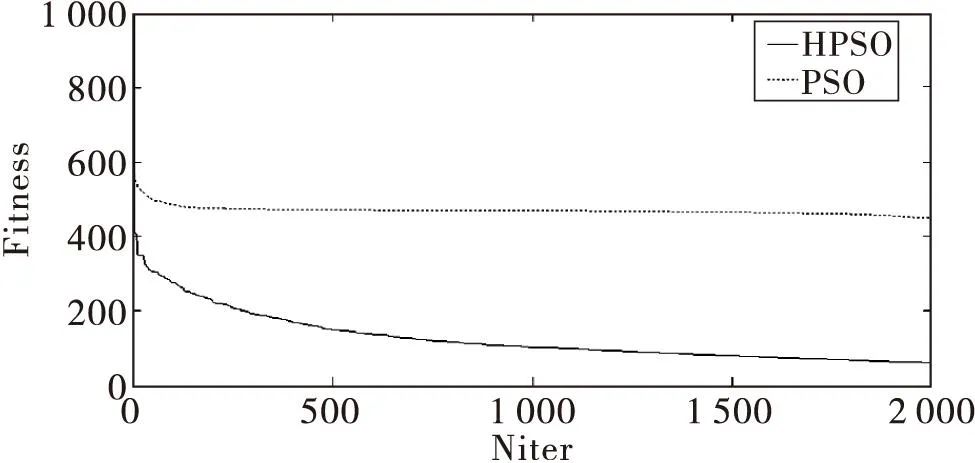
图4　Rastrigin函数在20维下的进化曲线

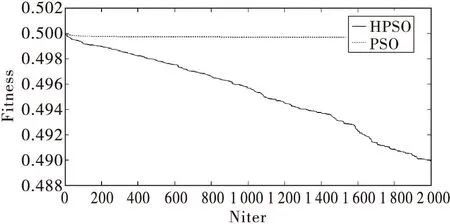
图5　schaffer函数在20维下的进化曲线

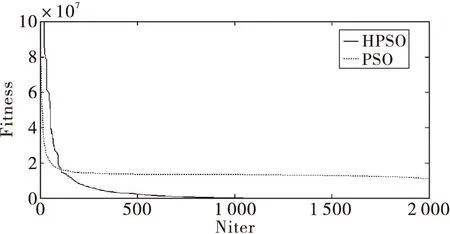
图6　rosenbrock函数在20维下的进化曲线

4结论

对基本的粒子群算法与莱维飞行和随机偏好游动相结合，利用莱维飞行搜索范围大、易跳出早熟收敛的优点和偏好随机游动的优势，弥补了粒子群易陷入局部极值点的不足，达到了改进的目的。对几个基准测试函数算法进行了仿真测试，并对改进算法与基本粒子群算法进行了比较分析。仿真结果表明了这种串行的改进粒子群算法解决寻优问题的有效性。

参考文献：

[1]RICARDO DE A L RABLO，MARCUS V LEMOS，DANIEL BARBOSA.Power System Harmonics Estimation using Particle Swarm Optimization[C]∥IEEE World Congress on Computational Intelligence.Brisbane，Australia，2012：10-15.

[2]JEHAD ABABNEH.Greedy particle swarm and biogeography-based optimization algorithm[J].International Journal of Intelligent Computing and Cybernetics，2015，8(1)：28-49.

[3]CLAUDIO FABIANO，MOTTA TOLEDO，LUCAS DE OLIVEIRA，et al.A genetic algorithm/mathematical programming approach to solve a two-level soft drink production problem[J].Computers & Operations Research，2014，48(2)：40-52.

[4]周明秀，程科，汪正霞.动态路径规划中的改进蚁群算法[J].计算机科学，2013，40(1)：314-316.

[5]欧阳喆，周永权.自适应步长萤火虫优化算法[J].计算机应用，2011，31(7)：1084-1087.

[6]李俊吉，崔志华，崔炎.空间分割微粒群算法[J].太原科技大学学报，2010，31(1)：19-24.

[7]张英杰，邵岁锋.一种基于云模型的云变异粒子群算法[J].模式识别与人工智能，2011，24(1)：90-96.

[8]ZAHRA BEHESHTI，SITI MARIYAM SHAMSUDDIN，SITI SOPHIAYATI YUHANIZ.Binary Accelerated Particle Swarm Algorithm (BAPSA)for discrete optimization problems[J].Journal of Global Optimization，2013，57(2)：549-573.

[9]GIFTSON SAMUEL G，CHRISTOBER ASIR RAJAN C.Hybrid：Particle Swarm Optimization-Genetic Algorithm and Particle Swarm Optimization-Shuffled Frog Leaping Algorithm for Long-term Generator Maintenance Scheduling[J].International Journal of Electrical Power and Energy Systems，2015，65(3)：432-444.

[10]YAHYA M，SAKA M P.Construction site layout using multi-objective artificial bee colony algorithm with Levy flights[J].Automation in Construction，2014，38(2)：14-29.

[11]李煜，马良.新型元启发式布谷鸟搜索算法[J].系统工程，2012，30(8)：64-69.

[12]王李进，尹义龙，钟一文.逐维改进的布谷鸟搜索算法[J].软件学报，2013，24(11)：2687-2698.

Hybrid Search Algorithm on Particle Swarm Optimization and Levy Flight

NIU Hai-fan，SONG Wei-ping，NING Ai-ping

(School of Electronic and Information Engineering，Taiyuan University of Science and Technology，

Taiyuan 030024，China)

Abstract：Particle swarm optimization algorithm has some weak points to solve multi-dimensional and complex optimization problems.Its convergence precision is not high enough，and it is easy to fall into local convergence.In order to overcome these problems，Levy flight and preference of rand walk are applied in the basic particle swarm optimization algorithm.The main method is to incorporate the updating equation of particle swarm optimization algorithm with levy flight and preference of rand walk in a serial fashion.The experimental results demonstrate that the improved algorithm has considerable advantages in search accuracy and the convergence speed while comparing with the basic particle swarm algorithm.

Key words：particle swarm optimization algorithm，levy flight，function optimization

中图分类号：TP183

文献标志码：A

doi：10.3969/j.issn.1673-2057.2016.01.002

文章编号：1673-2057(2016)01-0006-06

作者简介：牛海帆(1991-)，女，硕士研究生，主要研究方向为电磁兼容及故障诊断。

基金项目：太原科技大学博士科研启动基金(20142003)；太原科技大学研究生科技创新项目(20145019)

收稿日期：2014-12-29