基于VMD的抽水蓄能机组振动参数演化预测

樊玉林，桂中华，王明芳，安学利

（1.国网新源控股有限公司技术中心，北京100161；2.中国水利水电科学研究院，北京100038）

基于VMD的抽水蓄能机组振动参数演化预测

樊玉林1，桂中华1，王明芳1，安学利2

（1.国网新源控股有限公司技术中心，北京100161；2.中国水利水电科学研究院，北京100038）

提出了一种基于移动最小二乘响应面和变分模态分解（Variational mode decomposition，VMD）的抽水蓄能机组振动参数演化预测方法。首先利用移动最小二乘响应面建立抽水蓄能机组振动参数实时评估模型。然后利用VMD将复杂非线性的机组振动参数时间序列分解若干个平稳分量时间序列。其次对每个分量进行特性识别，根据其不同属性，分别采用LS-SVM或GM（1，1）对每个分量进行预测。最后重构每个分量的预测值获得原始时间序列最终的预测结果。实例分析表明，该方法能较准确地预测机组振动参数演化趋势。

抽水蓄能机组；振动参数；演化预测；移动最小二乘响应面；变分模态分解

1 研究背景

随着风电、光伏、核电等新能源的快速增长和特高压电网建设的全面提速，抽水蓄能电站的建设不断加快，在能源结构优化和绿色发展转型中发挥着重要作用。由于频繁的启停机及工况转换，抽水蓄能机组及易发生故障［1-5］。有效地获得机组的真实运行状态，对状态变化趋势更好地预测，及时发现机组异常，合理安排检修，是机组向状态检修转变的重要课题。

由于复杂背景环境的影响，抽水蓄能机组监测信号具有较强的非平稳性。小波分析［6-8］有较好的时频分析特性，但该方法是基于可调窗口傅里叶变换，存在能量泄漏。经验模式分解［9］（Empirical mode decomposition，EMD）具有高时频分辨率和自适应分解特性，但存在模态混叠、端点效应等问题。针对模态混叠问题，Dragomiretskiy和Zosso提出了变分模态方法［10-13］（Variational mode decomposi⁃tion，VMD），实现非线性、非平稳信号处理。

振动是影响水电机组正常运行及危害机组寿命的主要故障。强烈的振动会加速部件损伤，严重时会造成机组毁坏。因此，本文首先建立综合考虑运行工况的基于移动最小二乘响应面的抽水蓄能机组振动评估模型；然后利用VMD将非平稳的性能退化序列分解成若干个平稳的分量，分析各分量特性，分别采用LS-SVM或GM（1，1）来加以预测；最后重构所有分量的预测结果实现振动参数演化时间序列的预测。

2 移动最小二乘法

在拟合区域Ω的局部域Ωx上，设待求函数f（x）在Ωx内的N个采样点xI（I=1，2，…，N）处的函数值已知，即yI=f（xI）。在Ωx内f（x）近似为g（x）≈f（x），拟合函数g（x）的表达式［14］如下：

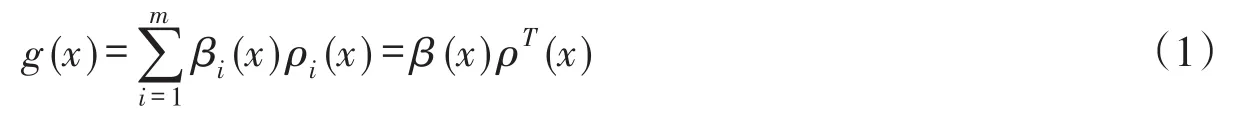
ρ（x）在二维空间中的二次基函数的表达式如下：

式中，m=6。

在移动最小二乘拟合中，采用加权最小二乘确定β（x），使g（x）在点x的Ωx内N个采样点的误差的加权平方和Ψ最小，即

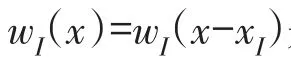
3 VMD方法

变分模态方法（Variational mode decomposition，VMD）主要包括构造变分问题及其求解过程［10-13］。假设信号f分解为k个具有中心频率的有限带宽的模态函数uk（t）。每个模态函数的带宽估计之和最小，约束条件为各模态之和等于信号f，则对应的约束变分问题可表示为：

将约束性变分问题变为非约束性变分问题，引入增广Lagrange函数去求上述约束变分问题的最优解。Lagrange函数可表示为：

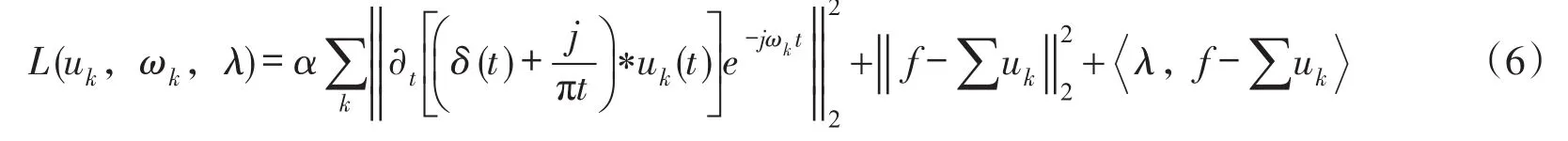
式中：λ为Lagrange乘法算子，α为二次惩罚因子。

Parseval/Plancherel傅里叶等距变换被采用将式（7）变换到频域，计算得到二次优化问题的解：

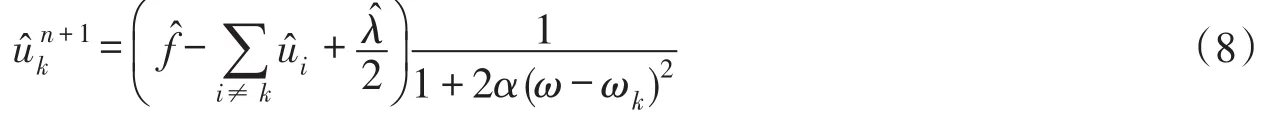
获得如下中心频率：

VMD方法的具体步骤可表示为：

（2）根据式（8）和式（10）更新uk和ωk。

（3）更新λ：

4 抽水蓄能机组振动参数演化预测模型

本文建立综合考虑运行工况，基于移动最小二乘响应面的抽水蓄能机组振动参数健康标准三维曲面模型ν=f（P，H），ν为机组状态参数，P为有功功率，H为工作水头。所构建的性能评估模型，具体步骤包括［2-3］：（1）建立机组健康模型。（2）机组振动参数退化时间序列。（3）采用VMD将振动参数变化时间序列分解为若干个平稳的分量。（4）根据每个分量的特征，选择适合其特性的预测模型进行预测。采用近似熵［11］辨识每个分量的特性，如果具有较强复杂性，用LS-SVM［15］进行预测；如果分量复杂性较弱，则用GM（1，1）［16］进行预测。（5）重构所有分量的预测结果，得到原始时间序列的预测结果。

5 应用实例

以某台抽水蓄能机组（单机容量250 MW；额定转速333 r/min；额定水头305 m）在2008年9月22日—2011年12月15日的实测状态监测数据为样本进行研究，验证基于移动最小二乘响应面、VMD、LS-SVM预测模型和GM（1，1）预测模型的抽水蓄能机组振动参数演化预测模型的有效性。选取该机组的上机架X向水平振动数据作为研究对象。

图1给出了2011年5月16日—2011年5月30日，振动实测数据。从图中可以看出，振动参数时间序列非常复杂，难以从图中准确地分析其真实运行状态。

图1 上机架X向水平振动实测数据

为实时获取蓄能机组的真实运行状态，对其建立健康状态模型。考虑到运行工况对机组振动特性的影响，以及移动最小二乘响应面对散乱数据良好的拟合性能，基于移动最小二乘响应面，建立机组振动-运行工况映射模型，获得机组健康状态下功率（P）、水头（H）和振动参数（ν）之间的映射关系ν=f（P，H）。

采用机组运行初期健康无故障数据，建立机组健康状态下振动标准模型。在2008年9月22日—2009年9月18日800组数据（覆盖机组可能的工作水头和有功功率）中，选取600组建立健康标准模型（为了准确反映机组振动与运行工况的映射关系，根据功率和水头的不同进行选择性的选取这600组数据，该选取方式的突出优点在于只需以少量的点便能使其所代表的映射关系具有足够的可信度），剩下的200组数据对模型进行验证。将200测试样本中的有功功率、工作水头输入模型，验证移动最小二乘响应面的拟合性能，计算平均相对误差为3.36%。

将机组运行2年后的状态监测中的工况参数等实时在线数据（2011年5月12日—2011年12月15日）代入机组健康模型ν（t）=f（P（t），H（t）），计算当前工况下的振动参数健康标准值ν（t），并和实测值比较，获得机组当前性能退化度D（t），如图2所示。从图中可以看出，机组振动性能开始劣化，其性能演化时间序列具有很强的非平稳性。

针对振动参数演化时间序列的非平稳性，采用VMD方法对图2所示时间序列进行分解，分解结果如图3所示。图中u2—u6为不同频率的分量，u1为低频趋势分量。从图中可以看出，分解后的分量有着比原始序列更好的规律性，能较好的反映性能退化趋势的特征。据分解后各分量变化规律，分别选用适合的预测模型进行预测，最后对它们进行重构，可以获得较为准确的预测结果。

图2 基于移动最小二乘响应面的水电机组振动变化趋势图

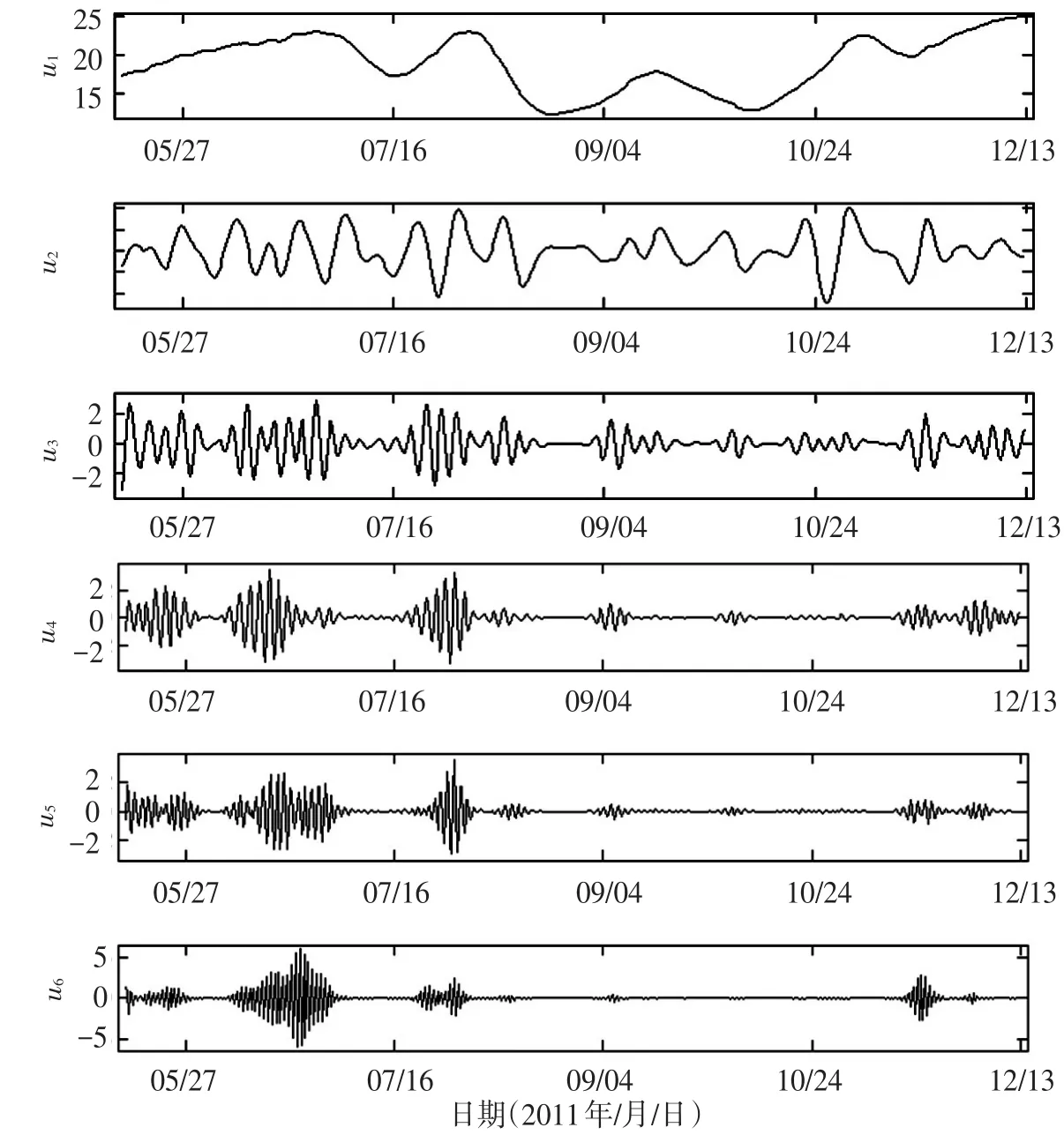
图3 基于VMD的振动变化趋势分解结果

以VMD分解后获得分量的前563个数据作为预测训练样本，后80个数据作为预测测试样本。计算u1—u6的近似熵，分别是0.097、0.564、0.483、0.325、0.285和0.178。可以看出，u2—u6的近似熵明显大于u1，说明u2—u6具有较强的复杂性，可用对非线性时间序列有较高预测精度的LS-SVM方法对其进行预测；采用GM（1，1）对低频趋势分量u1进行预测。计算u2—u6序列的嵌入维数，分别是8、10、7、11和8，对它们建立LS-SVM预测模型进行滚动预测，分别得到80组预测数据。应用GM（1，1）预测方法对u1进行预测，得到80组预测数据。重构所有预测结果，如图4所示。原始序列的近似熵为0.545，有较高的复杂度，采用LS-SVM对其进行预测，它的嵌入维数m=12，图4也给出了直接用LS-SVM对原始退化序列进行预测的结果。通过计算发现，采用基于VMD的混合方法进行退化预测时的平均相对误差为1.95%；而直接用LS-SVM进行性能退化预测时的平均相对误差为5.08%。结果表明，VMD混合方法具有更高的精度，能够应用于蓄能机组振动参数变化时间序列多尺度分析研究。

图4 振动参数变化预测结果

6 结论

变分模态方法（VMD）能将复杂非平稳信号分解为若干个平稳分量，它能很好的抑制模态混淆效应。针对抽水蓄能机组振动性能退化时间序列的非平稳性、非线性和波动性，采用VMD分离出序列中的若干个平稳分量。然后根据平稳分量的不同属性，分别采用适合的预测方法对其进行预测。最后重构每个分量的预测结果，完成振动性能退化原始时间序列的预测。将该方法应用于某抽水蓄能电站的实际监测数据中，结果表明该方法能较准确地预测机组振动参数演化趋势。

［1］An X，Pan L，Yang L.Condition parameter degradation assessment and prediction for hydropower units using⁃Shepard surface and ITD［J］.Transactions of the Institute of Measurement and Control，2014，36（8）：1074-1082.

［2］安学利，潘罗平，张飞，等.水电机组劣化趋势混合预测模型［J］.水力发电学报，2014，33（3）：286-291．

［3］安学利，潘罗平，张飞，等.水电机组状态退化评估与非线性预测［J］.电网技术，2013，37（5）：1378-1383．

［4］安学利，潘罗平，桂中华，等.抽水蓄能电站机组异常状态检测模型研究［J］.水电能源科学，2013，31（1）：157-160.

［5］安学利，潘罗平，张飞.基于三维曲面的抽水蓄能电站机组故障预警模型［J］.水力发电，2013，39（1）：71-75.

［6］Al-Badour F，Sunara M，Cheded L.Vibration analysis of rotating machinery using time-frequency analysis and wavelet techniques［J］.Mechanical Systems and Signal Processing，2011，25（6）：2083-2101.

［7］Ebrahimi B，Faiz J，Lotfi-fard S，et al.Novel indices for broken rotor bars fault diagnosis in induction motors us ing wavelet transform［J］.Mechanical Systems and Signal Processing，2012，30：131-145.

［8］An X，Jiang D，Zhao M，et al.Short-term prediction of wind power using EMD and chaotic theory［J］.Commuca⁃tions in Nonlinear Science and Numerical Simulations，2012，17（2）：1036-1042.

［9］Cheng J，Yu D，Tang J，etc.Local rub-impact fault diagnosis of the rotor systems based on EMD［J］.Mechanism and Machine Theory，2009，44（4）：784-791.

［10］Dragomiretskiy K，Zosso D.Variational mode decomposition［J］.IEEE Transactions on Signal Processing，2014，62（3）：531-544.

［11］An X，Yang J.Denoising of hydropower unit vibration signal based on variational mode decomposition and ap⁃proxi mate entropy［J］.Transactions of the Institute of Measurement and Control，2016，38（3）：282-292.

［12］An X，Zeng H.Pressure fluctuation signal analysis of a hydraulic turbine based on variational mode decomposition［J］.PIME，Part A：Journal of Power and Energy，2015，229（8）：978-991.

［13］张宁，朱永利，高艳丰，等.基于变分模态分解和概率密度估计的变压器绕组变形在线检测方法［J］.电网技术，2016，40（1）：297-302.

［14］张勇，李光耀，钟志华.基于移动最小二乘响应面方法的整车轻量化设计优化［J］.机械工程学报，2008，44（11）：192-196.

［16］曾杰，张华.基于蚁群优化的最小二乘支持向量机风速预测模型研究［J］.太阳能学报，2011，32（3）：296-300.

［17］Kayacan E，Ulutas B，Kaynak O.Grey system theory-based models in time series prediction［J］.Expert⁃Sys

Analysis of vegetation dynamic variations and response to climatic factor in Yangtze River Basin in recent decades

YU Zhilei，QIN Tianling，ZHANG Shuyu，SHI Wanli
（The Department of Water Resources，China Institute of Water Resources and Hydropower Research，Beijing100038，China）

Based on the MODIS data of the Yangtze River basin and precipitation and temperature series datasets of 204 weather stations（from 2000 to 2011），the correlation analysis was applied to study the rela⁃tionships among NDVI，precipitation and temperature on the scale of the Yangtze River basin and step re⁃gionalization，and then to exploit the main factors that impact the vegetation dynamic variations of the ecosystem of a basin，with a pixel as the calculating unit and Kriging interpolation method as the spatial anal⁃ysis method.The results show that：（1）In recent years，the temporal and spatial dynamics of NDVI vegeta⁃tion succession show a significant regularity.From the view of time，the mean NDVI change amplitude is：the second step＞the third step＞Yangtze River basin＞the first step.There are significant spatial ladder differences within vegetation successions in the Yangtze River basin.（2）Precipitation and temperature re⁃flect a strong spatial and temporal variability in the Yangtze River basin and Step regionalization.（3）The NDVI is negatively related to the precipitation and is positively related to the temperature of the overall Yangtze River basin.Although different step regionalizations have different results，the correlations between NDVI and precipitation are basically negative in different step regionalization and those between NDVI and temperature are significantly positive.In conclusion，the ecosystem vegetation presents a steady situation in the whole Yangtze River basin in recent years，and temperature is more important restriction factor to vege⁃tation growth.

NDVI（Normalized Difference Vegetation Index）；precipitation；temperature；the Yangtze Riv⁃er basin；step regionalization；correlation analysis

TV734.2

A

10.13244/j.cnki.jiwhr.2016.05.005

1672-3031（2016）05-0345-05

（责任编辑：祁伟）

2016-03-28

国家自然科学基金项目（51309258）

樊玉林（1972-），男，山西山阴人，学士，高级工程师，主要从事抽水蓄能电站自动化技术研究与管理工作。

E-mail：asiafrank@163.com

安学利（1980-），男，山东肥城人，博士，高级工程师，主要从事发电机组运行保障及故障诊断研究。

E-mail：an_xueli@163.com