基于聚类分析的入侵检测算法*

徐　超,王　芳,黄树成

(江苏科技大学计算机科学与工程学院,江苏镇江　212003)



基于聚类分析的入侵检测算法*

徐超,王芳,黄树成

(江苏科技大学计算机科学与工程学院,江苏镇江212003)

摘要:聚类技术在入侵检测中被广泛研究,但是传统的K-means算法对初始值敏感,无法取得理想的效果;层次聚类算法时间复杂度高,性能较差。针对这些问题,设计了一种改进的K-means算法:算法优化孤立点和噪声处理能力,根据有效性指标获得最优K值,在此基础上,动态选取初始聚类中心进行聚类,可以取得较好的聚类效果。采用数据集KDD Cup99将改进的算法应用于入侵检测,进行仿真实验。实验结果表明,改进的算法有效地提高了检测率和降低了误检率,与现有算法相比具有一定的优势。

关键词:聚类;K-means算法;入侵检测

修回日期： 2015-11-12

王芳(1971-),女,副教授。

黄树成(1969-),男,副教授。

作为网络与信息安全领域的一项重要技术,入侵检测(Instrusion Detection,ID)已经成为网络安全体系的一个重要组成部分。通过分析从网络和计算机系统中关键点搜集的数据,检测出可疑的访问、资源请求等可疑活动,从而发现是否有攻击存在,以保证系统资源的机密性、完整性和可用性[1]。误用检测和异常检测是现有的入侵检测系统常用的检测方法。误用检测用已知的入侵方法匹配并识别攻击;异常检测则将那些已经明显偏离用户正常使用系统方式的行为表示成异常行为。

数据挖掘能从海量审计数据中挖掘出正常和异常行为模式,这大大减少了人工分析和编码所带来的繁重工作,更提高了入侵检测系统的工作效率,因而,近几年数据挖掘技术被广泛应用于入侵检测领域。传统的基于数据挖掘的入侵检测系统完全依赖数据挖掘算法对已标记过的数据样本的学习,划分聚类中的K-means算法和层次聚类算法是较为常见的两种聚类方法。K-means算法能快速确定K个划分使得平方误差最小,具有较高的运算率,但K-means算法对初始值较为敏感,初始聚类中心的随机选择也可能会造成聚类陷入局部最优。而层次聚类方法比较符合数据的特性[2],聚类的质量比较高,但是时间复杂度较高。根据两种聚类方法各自在处理数据上的优缺点,学术界采用基于两种算法有机结合的混合算法,以达到既能降低聚类时间又能提高聚类质量的效果。如文献[5]中提出了一种改进的混合聚类算法H-K,解决了K-means算法中初始聚类中心选择的随机性和先验性的问题,但该算法对非球状簇的聚类效果较差,且时间复杂度较高[3]。因此,根据该算法的特点与不足,本文结合现有算法及有效性指标提出了一种改进算法。该算法首先针对K-means算法需事先提供聚类数K值以及初始聚类中心敏感进行改进,然后在聚类后期采用层次算法进行精细凝聚以提高聚类的质量,最后将改进的算法应用于入侵检测系统。实验表明，改进的算法具有较高的检测率和较低的误检率。

1入侵检测系统

入侵检测是对入侵行为的检查,通过收集网络和系统的网络行为、安全日志、审计数据等若干关键点信息,分析检测是否有违反安全策略的行为和被攻击的迹象。入侵检测提供了对内部攻击、外部攻击和误操作的实时保护,可以在网络系统受到危害前拦截和响应入侵。

图1　入侵检测通用模型

入侵检测系统(IDS)是用来检测系统或网络以发现可能入侵或攻击的系统,通过对网络传输进行实时检测,检查待定的系统漏洞、攻击模式、存在缺陷的系统或用户的行为模式,在发现可疑入侵时发出警告或拦截,是一种积极主动的安全防护技术。人们对IDS进行标准化,CIDF[6]阐述了一个IDS通用模型,将IDS分成四个组件,组件之间的交互数据使用通用入侵检测对象(简称gido)格式,模型如图1所示。

2聚类综述

2.1基本概念

“物以类聚,人以群分”,聚类(clustering)是数据挖掘的一种重要算法,是根据数据的内在相似性将未标记的数据集划分为多个类别,使类别内的数据相似度较大,而类别间的数据相似度较小。即聚类是将数据集划分为多个类或簇,使得数据样本具有较高相似度的为一簇,且不同簇中的数据样本不具备相似性。聚类的过程大致如图2所示。

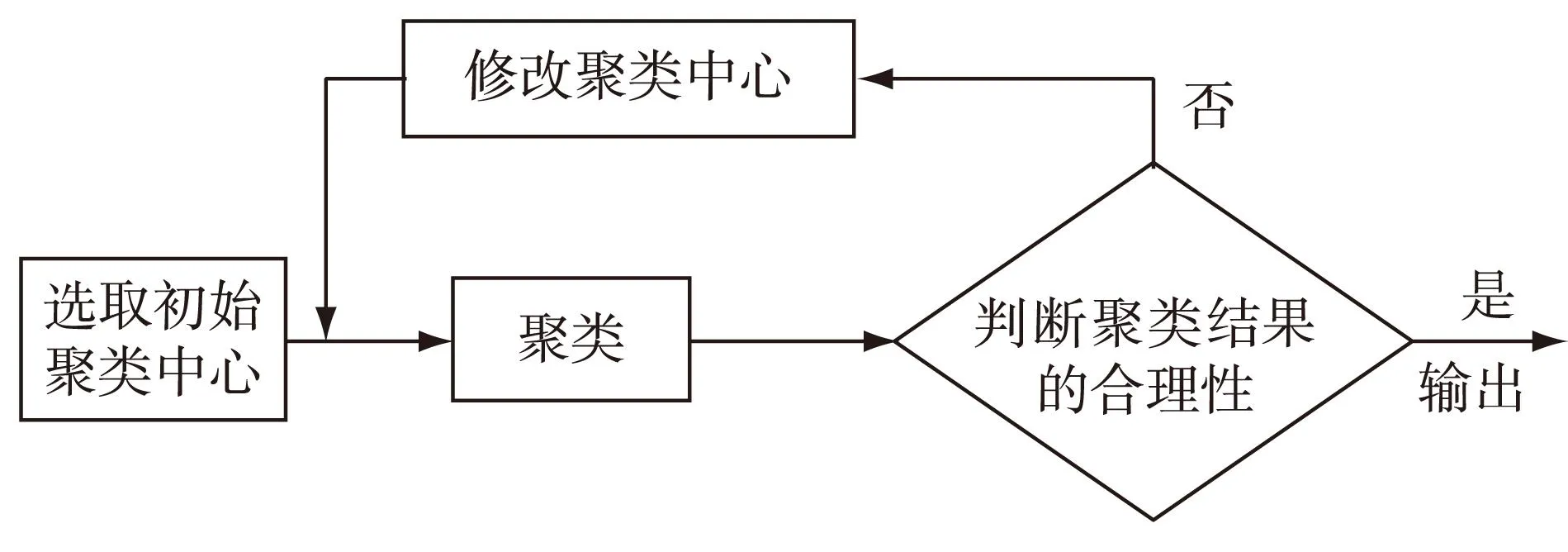
图2　聚类过程图

2.2聚类算法分类

聚类算法的选择取决于数据的类型、目的以及具体的应用,目前,并没有一种算法达到普适的效果。现有聚类算法大致分为划分式聚类算法、层次聚类算法、基于密度的聚类算法、基于网格的聚类算法、基于模型的聚类算法以及基于谱图理论的谱聚类算法等[4]。

划分式聚类算法是最基本的聚类算法,最常用的是K-means算法,其基本思想是:首先从N个数据对象中随机选择K个数据对象作为初始聚类中心,而对于余下的每个对象,根据其与各个聚类中心的距离或相似度,分别将它们分配给与其最相似的聚类;然后重新计算每个聚类的平均值,寻求新的聚类中心。这个过程不断重复,直到各个聚类中心不再变化或标准测度函数开始收敛。

层次聚类方法可分为凝聚层次聚类和分裂层次聚类。其中凝聚是一种自底向上合并的方法,基本思想是:首先把每个数据对象作为不同的簇,然后不断使用基于簇的代表点的方法对最相似的两个簇进行合并,直到簇的数目达到了用户指定的阈值。

3算法的改进

3.1K-means算法的缺点

K-means算法对大型数据集的处理效率非常高,当样本分布呈现类内团聚时,聚类效果更好。K-means算法以确定聚类数K和选取的初始聚类中心为前提,使得各样本对象到其所判属的聚类中心距离平方之和最小。但是,K-means算法存在着一定的缺陷:1)易受孤立点和噪声的影响。算法对于数据集中的孤立点和噪声比较敏感,对聚类结果可能会产生较大的影响;2)事先需给出K值,K值的选取难以界定;3)随机选取的K个样本作为聚类中心,对于一些结构较为复杂的数据集来说,聚类结果可能不稳定,产生错误的聚类结果。

3.2优化孤立点和噪声的处理能力

K-means算法会因为噪声和孤立点的存在,而导致差异较大的聚类结果,从而影响算法的执行效率和准确度。在这里,对算法进行了改进,对数据集进行初始划分,降低噪声和孤立点的影响。

定义1设X为数据集,X={x1,x2,…,xn},假设n个样本数据被聚类成S类,聚类中心个数为K,定义数据xi到其它样本数据的距离和为

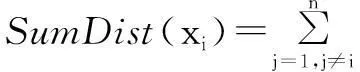
(1)

其中，‖·‖2表示平方欧氏距离。

定义2设X为数据集,X={x1,x2,…,xn},假设n个样本数据被聚类成S类,聚类中心个数为K,定义数据集X中距离和的均值为

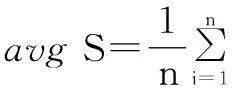
(2)

算法(简称优化算法A)描述如下:

1) 计算每两个数据之间的欧氏距离,得到距离矩阵D,再依次计算各个数据的距离和SumDist(xi)以及数据集的距离和的均值avgS;

2) 去除距离和SumDist(xi)大于均值avgS的点,即去除孤立点和噪音数据,从而得到一个新的样本数据集X′及距离矩阵D′;

3) 将步骤2)得到的结果构造最小生成树,按权值降序排列,删掉K-1个分支,从而得到K个子簇。

4) 计算各子簇的数据的算术均值作为K个初始聚类的聚类中心。

算法分析:实验证明,利用该算法得到的初始聚类中心较为接近迭代聚类的收敛聚类中心,且数据点尽可能地分散,删掉了孤立点和噪音的影响,取得了较好的划分聚类结果。

3.3K值的确定

K-means算法事先需要给出聚类数K值,但K值的选取估计,不准确的K值会影响最终的聚类效果。在这里,为了有效地选取更为合适的K值,提出了一种K值有效性指标[7],用以评估聚类结果以及确定K值。

定义3设X为数据集,X={x1,x2,…,xn},假设其中的k个样本数据被聚类划分成类Si,Si={s1,s2,…,sk},定义类内距离Bet(Si)为类Si中任意两个数据x,y的距离平方和:

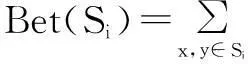
(3)

定义4设X为数据集,X={x1,x2,…,xn},假设其中的k个样本数据被聚类划分成类Si,Si={s1,s2,…,sk},定义类间距离Wit(Si,Sj)为类Si到其他类Sj的距离:

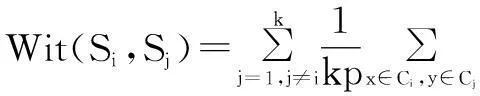
(4)

其中，k、p分别为类Si和类Sj中的数据对象个数,x、y分别为类Si和类Sj中的数据对象。

定义5设X为数据集,X={x1,x2,…,xn},假设其中的k个样本数据被聚类划分成类Si,Si={s1,s2,…,sk},定义BW(S)为K值有效性指标:

(5)

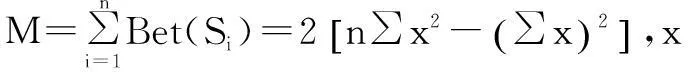
K值有效性指标反映了聚类结构的类内紧密性和类间分离性,从类内紧密的角度上看,样本的类内距离Bet(Si)越小越好,从类间远离的角度上看,样本离近邻聚类的距离,即类间距离Wit(Si,Sj)越大越好,使用线性组合方式平衡二者的关系,当BW(S)最小时,类内紧密和类间远离达到一个平衡值,对应的就是最优聚类的划分,此时的K值就是最优聚类数。

3.4基于最优聚类数的K-means算法改进

通过去除孤立点和噪声的影响的处理优化以及K值的确定,下面将上述的改进方法进行有机结合得到一种改进的K-means算法,其基本思想是:首先由K值的有效性指标确定K值,算法过程中运用到优化算法A来进行初始聚类优化,然后再迭代计算出K个聚类中心,最后调用层次算法进行精细凝聚检验。其算法的主要步骤如下:

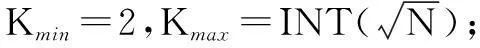
2) FOR K=Kminto Kmax,调用优化算法A,得到初始聚类划分S,及所有K值集合,计算每个数据对象到每个聚类中心的聚类,并将它赋给离它最近的类;

3) 利用聚类结果,计算各个K值的有效性指标BW(S),比较有效性指标值,BW(S)达到最小时,所对应的K值即为最优聚类数,该值所对应的聚类划分就是初始聚类中心;

4) 重复步骤3),将每个数据对象赋给与它距离最小的类,聚类出子簇,重新计算每个簇的平均值,直到满足终止条件;

5) 调用层次凝聚算法进行精细凝聚,利用整体相似度合并子簇,评价合并前后的聚类质量,聚类质量下降则取消合并;

6) 直到收敛不再发生变化。

4实验研究与分析

4.1入侵检测模型

入侵检测是检测系统及时发现违反安全准则的入侵行为并报警采取相应的防护手段的行为。入侵检测系统分为训练部分和异常行为检测部分[8]。

训练部分是:将训练数据输入到系统中,系统自动生成聚类结果,再对聚类结果进行分析标示。

异常行为检测部分:将需再检测的数据对象先进行标准化处理,用改进的K-means算法生成正常行为模式库,即计算处理后的数据到各个聚类中心的距离,赋给离它最近的聚类中,若这个聚类标识为正常类,则该数据对象为正常数据,否则为异常数据。这样有效地提高了系统的检测率,降低了误报率,实现了一个高效的入侵检测系统。

基于聚类分析的入侵检测模型如图3所示。

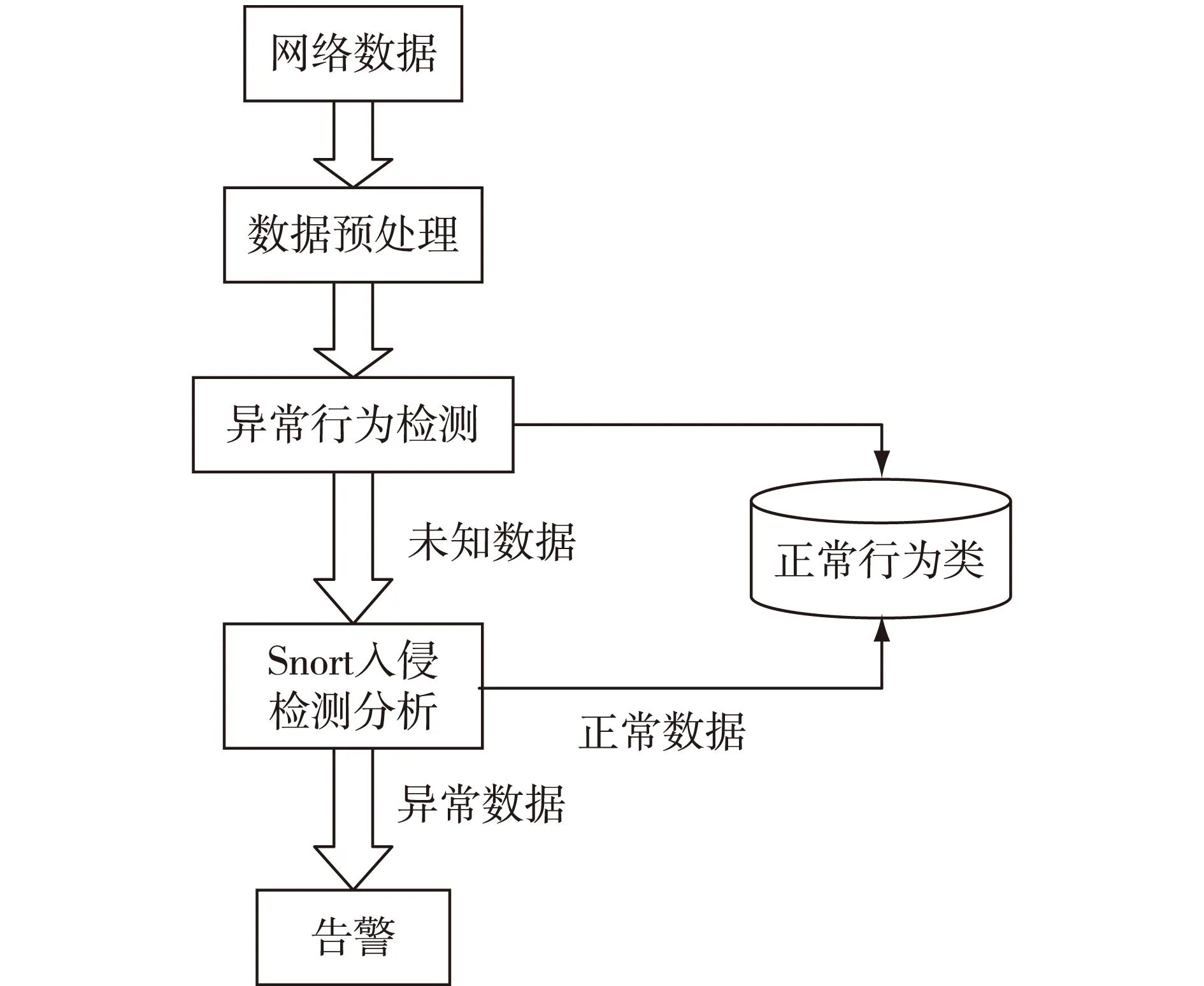
图3　基于聚类分析的入侵检测系统模型

本文采用经典的KDD Cup99数据集作为网络数据进行验证,选取Snort入侵检测系统为基础,经过预处理模块使数据标准化,将其转化成合适的数据格式,并对数据进行除噪等操作,使用改进的K-means算法进行聚类,将包含大量数据的类标识为一个正常行为类,而包含小量数据的类则为异常类。然后将异常类作为未知数据传给Snort入侵检测[9]分析模块,利用其规则库对未知数据进行再检测,对异常数据进行告警,而将未匹配的数据归到正常行为类中。该模型提高了入侵检测系统的检测速率。

4.2实验结果与分析

为了测试基于改进的划分算法的入侵检测系统的性能,本文实验采用KDD Cup99数据集中的kddcup-data-10percent数据包对检测算法和入侵检测模型进行了仿真实验,并对结果做出相应的分析。

入侵检测的性能可以用检测率(Detection Rate,DR)和误报率(False Positive Rate,FPR)进行描述:

(6)

(7)

数据预处理:kddcup-data-10percent数据集是KDD Cup99的10%抽样,每条数据由41个特征属性和一个决策属性构成[10],决策属性是每条数据的所属类别,在测试时仅作为判断条件。数据集中包含有符号型的数据属性,不适合本文的聚类测试,且实验所使用的Matlab平台不识别字符,所以需进行数据预处理,将数据位经过数值化和归一化后,才可用来测试。

每次实验时,根据数据集中的种类比例分配,随机选取了8324条数据,其中,正常数据为6992条,异常数据为1332条,标记为数据集D。多次测试得到一个平均记录,如表1所示。

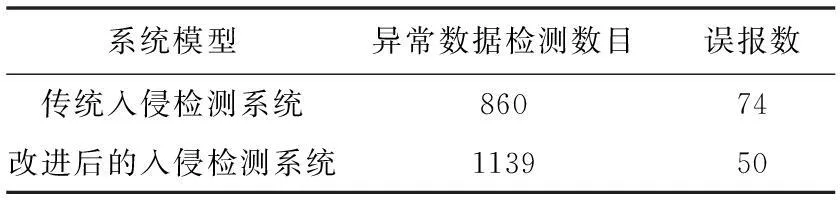
表1　入侵检测结果

经式(6)和式(7)计算可知,改进前后的入侵检测系统的检测率和误检率如表2所示。

表2　实验测试对照表

由上述实验数据表明,采用了基于改进的K-means算法的入侵检测系统是有效而且可行的,本文的入侵检测系统提高了检测率,降低了误报率,优于传统的入侵检测系统。

5结束语

入侵检测技术是计算机网络安全的重要保障,本文提出了一种基于改进的K-means算法,设计了入侵检测系统。针对传统K-means算法的不足之处,采用有效性指标来确定K值的选取,并动态地获取初始聚类中心,进行了孤立点和噪音的删除处理,降低其影响,降低了聚类的迭代次数,有效地提高了聚类效果。基于改进的划分算法的入侵检测模型运用了传统的Snort入侵检测模型,结合改进的K-means算法进行异常行为检测,提高了入侵检测系统的性能。

经测试证明本文所提出的改进的K-means算法在入侵检测方面具有可行性和有效性,优于传统的入侵检测系统。

参考文献:

[1]谢卓.基于聚类学习算法的网络入侵检测研究[J].现代电子技术，2012,35(2):80-93.

[2]ALMEIDA J,BARBOSA L,PAIS A,et al.Improving hierarchical cluster analysis:a new method with outlier detection and automatic clusterint[J].Chemometrics and Intelligent Laboratory Systems,2007,87(2):208-217.

[3]郝洪星,朱玉全,陈耿,李米娜.基于划分和层次的混合动态聚类算法[J]. 计算机应用研究,2011(1):3-4.

[4]Kamber M.数据挖掘:概念与技术[M].韩家炜,译.北京:机械工业出版社,2012:338-467.

[5]LIN Cheng-ru,CHEN M S.Combining partitional and hierarchical algorithms for rubust and efficient data clustering with cohesionself-merging[J].IEEE Trans on knowledge and Data Engineering,2005,17(2): 145-159.

[6]周继军,蔡毅.网络与信息安全基础[M].北京:清华大学出版社,2008：205-207.

[7]周世兵.聚类分析中的最佳聚类数确定方法研究及应用[D].无锡：江南大学博士学位论文,2011.

[8]夏战国,万玲,蔡世玉,孙鹏辉.一种面向入侵检测的半监督聚类算法[J].山东大学学报(工学版),2012(6):2-4.

[9]傅涛,孙亚民.基于PSO的K-means算法及其在网络入侵检测中的应用[J].计算机科学,2011,38(5):54-56.

[10]袁利永,王基一.一种改进的半监督K-means聚类算法:研究综述[J].计算机工程与科学，2011(6):1-3.

Intrusion Detection Based on Improved Partitioning Algorithm

XU Chao, WANG Fang, HUANG Shu-cheng

(School of Computer Science and Engineering, Jiangsu University of Science and Technology, Zhenjiang 212003, China)

Abstract:Clustering technique has been extensive researched in intrusion detection, but the traditional k-means algorithm is sensitive to initial values,unable to obtain the ideal effect. Hierarchical clustering algorithm time complexity is high and poor performance. To solve these problems,an improved K-means algorithm is presented in this paper. Outlier and noise processing capacity are optimized. The initial clustering center are selected dynamically, according to optimal K values which is obtained by the effectiveness indicator. The KDD Cup99 datasets is applied to conduct simulation experiment on the application of the improved algorithm in intrusion detection. The experiments show that the detection rate is improved effectively and the false positive rate is reduced. The improved algorithm than the existing algorithm has certain advantages.

Key words:clustering; K-means algorithm; intrusion detection

作者简介：徐超(1990-),女,江苏赣榆人,硕士研究生,研究方向为数据挖掘。

*基金项目：国家自然科学基金(61572498)

收稿日期：2015-10-30

中图分类号:TP311.13

文献标志码:A

DOI:10.3969/j.issn.1673-3819.2016.01.013

文章编号：1673-3819(2016)01-0057-04