基于案例推理的指挥实体任务规划高维解空间适应性问题研究*
张 媛,齐玉东,乔勇军,陈青华
(海军航空工程学院,山东烟台 264001)
基于案例推理的指挥实体任务规划高维解空间适应性问题研究*
张媛,齐玉东,乔勇军,陈青华
(海军航空工程学院,山东烟台264001)
摘要:利用案例推理对指挥实体任务规划过程中决策问题求解方法的修正过程是该方法推理过程中最困难的阶段,尤其当决策问题解空间是多维的情况下。讨论了指挥实体任务规划过程中高维决策空间的修正问题,并提出了可行的解决方法。首先,利用自组织匹配法清晰展现问题空间与决策空间的映射过程,然后,利用反向传播神经网络分析匹配结果间的相关性问题,最后,选取一个简化的军事剧情对该方法的合理性进行验证。
关键词:案例推理;高维解空间;适应性;自组织匹配法;任务规划
修回日期: 2015-10-20
齐玉东(1973-),男,副教授。
乔勇军(1973-),男,副教授。
陈青华(1979-),女,讲师。
案例推理CBR(Case-Based Reasoning,CBR)方法是一种模仿人类思维过程的计算方法,因此,在军事决策仿真中常用CBR方法来模拟指挥员的决策过程。但是,指挥实体任务规划的决策空间是一个多维空间,并且决策仿真过程中选取的案例不可能穷举所有情况,因此案例的选取又具有有限性。虽然里克[1]、Hanney 和 Keane[2]以及Jarmulak等人[3]对利用CBR方法模拟指挥员决策过程中的案例修正方法提出了必要的建议性意见。但是他们所提到的解决方法都是“ 知识启发式方法”[4],即对CBR系统的自身案例进行修正性学习,并把它们作为知识库建立的来源。即知识启发式修正方法必须由CBR系统提供足够数量的多种知识来支撑。不充足的知识储备可能会对系统造成负面影响。此外,由学习算法产生的修正知识必须正确,并适当结合已有的修正单元、解析过程,必要的时候也要考虑一下矛盾情况和不相匹配的情况,无法满足决策仿真过程中选取的案例不可能穷举所有情况的前提。并且许多CBR系统的决策空间只是一维的,例如对财产的估值,或对案例的评估分析等[5-8]。但是,在利用CBR技术来解决军事行动方案的制定问题COA(course of action)时,每一行动路线由相应时间所对应的实体位置来表示,因此所建立的案例决策空间是一个多维空间。这个多维空间可以简单认为是由若干个单维空间组成,每个单维空间应用相同的方法,然后再将每个单维决策结果进行组合。然而,这种思路可能会认为COA是一个由多个独立决策单元组成的结合体,这明显是错误的。
针对上述情况,本文提出了一种解决高维案例空间中有限案例之间的适应性问题,即利用自组织匹配SOM(Self Organizing Map,SOM)和ViSOM(Visualization induced Self Organizing Map,ViSOM)相结合的案例修正方法以解决类似情况下的案例修正问题。
1SOM 和 VISOM
SOM是一种被模式识别、图像分析和误差诊断等领域广泛应用的无人监督神经网络算法。基本的SOM算法受到人脑直觉思维模式的启发,通过神经元将感知印象映射到大脑立体空间或形成神经元色质间的立体空间关系。这就是所谓的竞争学习。SOM算法是由两层神经元组成:具有n个输入节点的输入层(表示N维输入向量)和m个输出节点的输出层(表示M个决策范围)。每一个输入节点都与一个输出节点相连接,所有的连接关系都会赋予相关的权重,因此SOM就形成了一个将高维数据整合成低维网格的非线性投影图。基本过程如下。
1) 初始化:随机赋予全部神经元的权重向量值。
2) 相似性匹配:运用角距离公式或欧几里德距离公式。计算模式xi与模式xj之间的欧几里德距离dij为

(1)
其中,dij越小,表示向量就越接近。角距离是基于向量的内积:
(2)

式中,这里cosθ值越大,向量的相似度就越接近。所以我们就可以发现时间t时最佳匹配值i(x)为

(3)
其中,wj为映射层的权重向量。
3) 更新:利用更新公式调整所有神经元的突触权重向量:
wj(t+1)=η(t)[(dr-dj)·wj(t)],
(4)
其中,j∈Ni(x),否则,不变。
其中,η(t)表示当前t时刻神经元的学习率;Ni(x)是一个以最佳匹配值i(x)为中心的邻域方程,这个最佳匹配单元和它的邻域都可以通过修正当前输入的参考向量值来对输入进行表示。学习单元的大小由其邻近的影响函数来决定,这个影响函数在映射网格中是一个从最佳匹配单元进行单元距离递减的函数。最大权重的修正过程就是最佳匹配值正向产生的过程,并且根据正向产生过程中节点j和节点dj之间的距离,以最佳匹配点为始,直到某一径向距离dr处,权重修正值经过微调降为0(N中的最大允许距离)。这种效应可以通过高斯函数方便地实现:
(5)
为了加快计算的速度,可以使用Λ函数,这个函数规定在半径r范围内的神经元只能进行恒等的正向权重改变。
4)延拓。在过程2)执行基础上,通过训练过程中对参数η和Λ进行动态计算,直到其没有显著变化为止。学习进程开始时,邻域的半径相当大,但它会随着学习过程的开展而有所收敛。这保证了学习开始时就对全局次序进行确定,随着过程的结束,半径变得越来越小,匹配表中模型向量的局部修正过程将更具体。
SOM算法最重要的典型特征就是保持映射过程的拓扑性。Bauer和Pawelzik[9]和Kohonen等人[10]采取各种测量方法,将高维数据映射到低维特征图(一维或二维特征地图),同时文献[11]和文献[12]也相继提出了提高SOM算法的拓扑可维护性方法。然而,SOM算法不会一直可靠地描述数据及其结构分布,因此需要采取一些措施来计算特征图的质量以便得出最好结果。平均量化误差表示矢量数据与其原型之间的平均距离。一般来说,当特征图的尺寸增加时,就需要有更多的单元来对其数据进行表示,因此每个数据向量越会更接近其最佳匹配单元,从而两者之间的平均量化误差就会越小。
ViSOM使用与标准SOM类似的网格结构,两者的不同之处在于前者更新理想点邻域中神经元权重值的方式如方程(6)所示:
wk(t+1)=wk(t)+α(t)η(v,k,t)[x(t)-wv(t)]
(6)
其中,η(K,T,V)是邻域函数,而ViSOM利用公式(7)对理想点邻域中神经元权重值进行更新:
wk(t+1)=wk(t)+α(t)η(v,k,t)[x(t)-wv(t)]+
劳动争议调解员采用换位思考法进行调解,也可体现在调解协议的达成过程中,即在提出调解方案或引导当事人达成调解协议时,站在当事人的立场,设身处地、将心比心地思考矛盾产生的原因、解决问题的关键和当事人所能接受的向对方让步的底线,从而提出当事人都能接受的调解方案,或促使当事人达成调解协议。
(7)
其中,wv(t)为时间t时理想神经元的权重值;dvk为输入空间中神经元v和神经元k间的距离;Δvk为特征图中神经元v和神经元k间的距离;λ为预先指定结论参数的相对值。这个值越小,表明得到的特征图决策质量越高。
ViSOM的关键特征在于特征图中神经元之间的距离可以反映出原始数据空间对应点间的距离。我们在案例问题空间及其决策空间中都采用了ViSOM理论。一旦这两类空间中都采用ViSOM算法,那么案例问题空间中的案例位置就是ViSOM算法的输入,决策空间中相应案例的位置就是ViSOM算法的输出。由于位置变量是一个二维向量,因此BP网络结构比直接输入原数据库所采用的BP网络结构简单得多。这种方法试图分别模仿问题空间作为输入模型和决策空间作为输出模型的过程,并且通过调整连接权重值的大小将问题与其决策结果关系相映射。
ViSOM算法的输入为案例问题空间中每对案例位置间的位置差异,而非实际位置点。同样,案件决策方案中同一案例对间的位置差异作为ViSOM算法的输出。目标案例与其最相似案例间的区别经过训练后作为神经网络的输入。同样得到决策空间特征表中目标方案的位置信息。
由于ViSOM算法保留着特征图中输入数据各点间的距离信息,因此离目标案例最近的案例就是所采用的目标案例决策结果。在实验中,我们采用了一个三层BP神经网络,此神经网络由2个元素构成输入向量,5个神经元构成隐藏层以及2个神经元构成输出层,tanδ函数作为各层间的传递函数,训练过程采用适用于小型神经网络的快速训练方法——trainlm算法(莱文博格-马夸特算法)。
2目标案例解的求解
在获得ViSOM案例决策空间中目标案例的位置后,如果同一位置没有预期存在的案例信息,那么这个案例的决策方案就作为目标决策结果。如果同一位置不只存在一个预期案例,那么这些预期案例决策结果的平均值就是目标案例的决策结果。但是,当在这个位置上没有预期案例存在时,我们采取下几种可能的解决方式从相应高维决策方案中寻找准确决策结果的位置。
首先,建立ViSOM案例解空间中对应节点的向量原型。一旦对ViSOM解空间进行训练,解空间中每一个节点都会有其对应的原型向量。当ViSOM解空间中目标案例的位置已知时,对应节点就可能成为目标案例解的理想节点,并且此节点的权重大小可能对输出结果具有一定的影响。
其次,使用反向距离加权的K-近邻法(K-Nearest Neighborhood, KNN)算法。需要注意的是,此算法使用的是目标案例位置间的距离和决策空间特征图中的相邻距离,而非问题空间中的距离。
3实验设计
我们将一个COA表示作战兵团中一个作战指挥官,选取MAK VR-Forces软件作为仿真环境。通过利用VR-Forces软件中实体的位置及其到达此航路点所对应的时间表示一个COA的决策制定过程。换句话说,一个COA是由一个相当于人类指挥官指挥过程公式化表示的同步矩阵进行表示的。其中,矩阵是由仿真过程中不同时间段上所对应的实体航路点组成:其中行表示实体,列表示时间段。
本文利用VR-Forces软件产生一个剧情作为测试实例。剧情设计为4个敌方坦克(BMP 1,3 T80,BMP2,BMP2和2)部署在一个雷区后面。我方用3个排(每排拥有4辆坦克,分别用蓝排,红排和白排进行标识)对敌方坦克进行压制,同时安排两个工程车辆进行扫雷。
作战想定如图1所示。

图1 攻防剧情
蓝排:原地待命,随时准备向敌军开火。
红排:向红排航路点挺进,为工程兵排雷提供掩护。
白排:向白排航路点挺进,为工程兵排雷提供掩护。
工程兵:紧随红排其后,当红排到达红色路线点,并且敌军被摧毁后,工程兵挺进雷区进行排雷。
3.1情景描述
在有关CBR系统军事案例中,案例来自于实战训练科目安排,先验知识,战术及其作战条例[13]。根据领域知识和经验,任务、敌人、地形、部队和时间(METT-T)通常是人类指挥官真实作战过程中考虑的因素。本剧情中,在保持突破雷区任务不变的情况下。为了简化剧情的表示形式,本项目中不需要对任务进行描述,只是由一个符号对象来对每个实体进行表示。即使这样,也仍然无法比较敌对双方的能力大小。因此我们对每组兵力采取综合表示而非分别表示的方式,即利用简化的方式,通过定义其兵力比例等级来表示其能力大小。例如T80坦克的能力为5,M1A2的能力为6,BMP2的能力为3。同时,把战斗效能认为是一组有序数据而非符号。因此,“全能”用1表示,而“无法使用”用0表示和“退化”用0.5表示。然后兵力比例等级由公式(8)给出:
(8)
其中,Ti为友方兵力第i队的能力,Cti表示友方兵力第i队的战斗效能。Ej为第j个敌方兵力的能力,Cej表示第j个敌方兵力的战斗效能。
VR-Forces仿真过程中,整个仿真战场中实体的位置都使用网格坐标系中(x,y)网格信息来表示一个实体的位置,不在网格单元中心的实体将被分配到最近的网格单元上。
我们用矩阵存储所有实体的网格信息。如果某一网格单元中没有实体,就将这个网格单元位置赋予0;否则表示此网格单元存有实体。表1中,仿真战场中产生实体a和实体b,定义相应的矩阵为

对于每一实体的数据表示方式主要有两种:一种为分类数据的表示方式,另一种为数据的表示方式。例如有两种敌方实体:BMP2和T80。每类实体的数量可能有所不同。若采用分类数据的表示方式,假设用1代表BMP2,用2代表T80。那么敌方兵力就可以用一个含有0,1,2三种元素构成的矩阵来表示。若采用数据的表示方式,那么实体的位置就可以根据其在坐标系中的位置来进行存储。例如,实体A=(3,2)和B=(5,4)的表示如表1所示。

表1 网格表示
第二种方法更适合表示实验方案中的友军信息。假设友军部队主要有4个角色组成:蓝排,红排,白排和工兵。为了简化决策的过程,文中忽略了案例表示中的时间,采用(X,Y)两维坐标进行表示友军部队兵力的位置(假设地形是确定的,并且每一兵力同时到达每一航路点)。表2显示了此剧情中对所有实体兵力的表示。

表2 剧情表示
3.2案例决策
正如前面所讨论的,COA可以用剧情中由不同时间步长所对应实体的航路点位置所构成的矩阵来进行表示:每一行对应一个实体,每列对应一个时间步长。对于这个简单的剧情,我们使用案例所描述的4个路线来表示决策部分:蓝排路线,红排路线,白排路线和工兵路线。每条路线由相应时间段的5个航路点组成,包括开始点和结束点,每个航路点由X和Y两维坐标进行表示,如表3所示。

表3 军队行进路线表示
3.3数据收集
为了收集案例数据库的输入数据,我们随机对300个案例进行描述,其中随机产生的案例值包括兵力比例能力初始值以及敌我双方的位置初始值。然后根据每个案例的描述,选取一个具有通用感知能力的COA并用VR-Forces软件对其进行仿真。进而对作战目的是否达到、敌方剩余(开火)力量和友军的剩余力量等结果进行记录。选取上述影响因素中具有最大权重W值的COA作为最合适的解决方案,有
(9)
其中,w1,w2是领域知识定义的权重;G表示目的是否达到;fr表示友军剩余力量;er表示敌军剩余力量。
因为本剧情不可能穷举所有部署情况下的所有敌方计划,因此他们的路径也可以改变。我们需要选择不同情况下,覆盖了大部分剧情变化情况下的案例。图2和图3显示了两个例子。
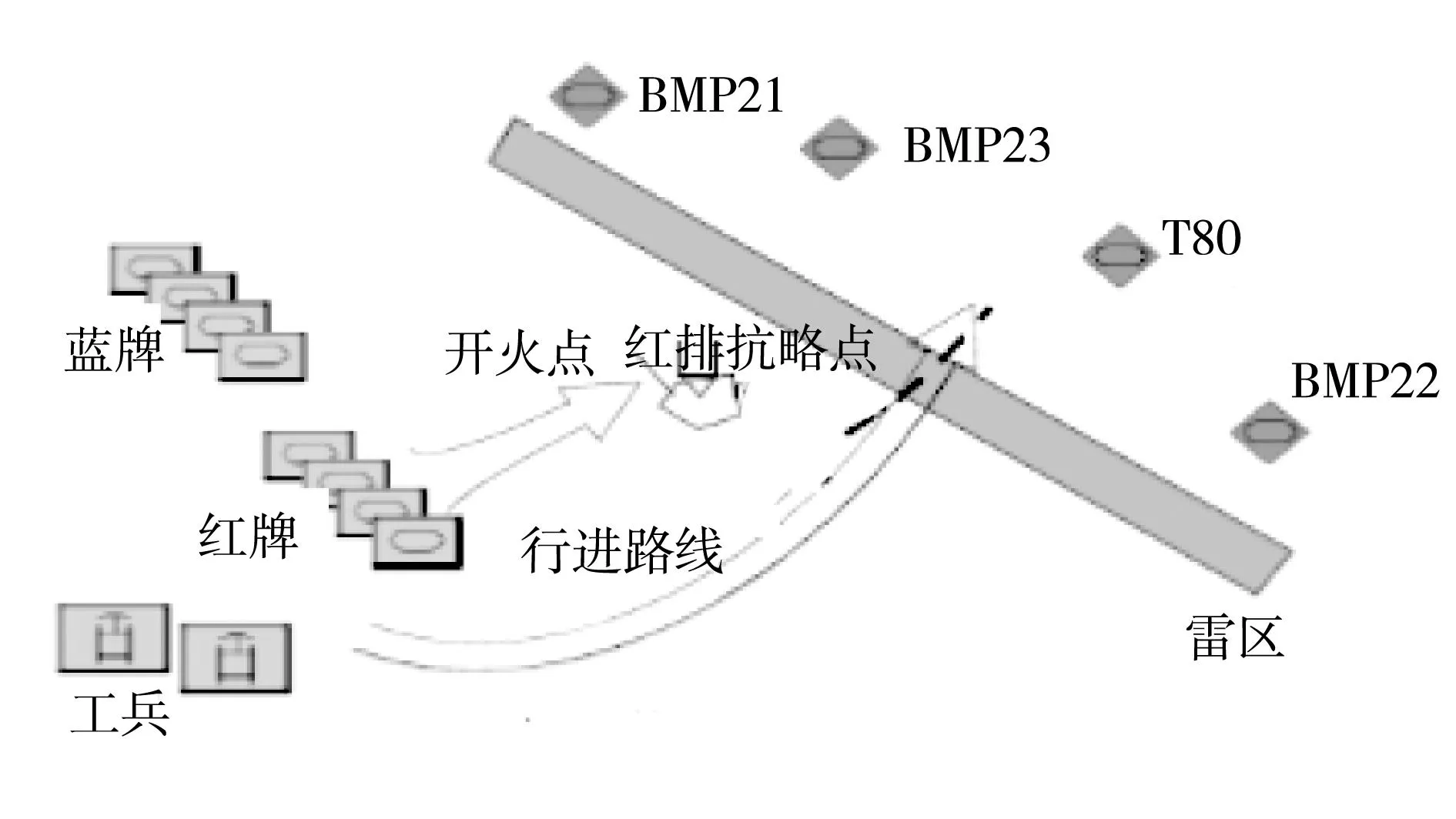
图2 缺省情况下的练习变化1(白排没有参加行动)

图3 缺省情况下的练习变化2(敌人的火力比友方军队火力强)
4评估分析
由于缺乏大量的军事决策支持系统,甚至基于不同剧情数据的类似项目支持也很少,所以确立一个应用标准就变得很困难。领域专家的评估方法是最直接的一种方式,如军事方面的资深专家。我们可以对评估案例进行图灵测试,进而结合军事方面资深专家的建议进行相应输出结果的比较。一个比较实际的方法就是利用VR-Forces软件对所生成的COA进行仿真模拟,以发现对应的COA是否能够帮助友军部队达成其作战目标,并将反馈结果反向输入到系统中以提高系统的学习能力。
本文将案例库中的300个案例分为两组:一组用于训练,另一组用于评估。训练组中的案例作为ViSOM和BP神经网络训练系统的输入,同时评估组中的案例用于判断训练组输出结果的优劣。
实验中所选取的案例是按照2:1的比例进行划分的。因此,随机抽取200例作为训练集,其余100例组成评估集合。评估过程重复10次,结果如表4所示。其中,平均误差(ME)就是这100个案例中COA的预测值与其真实值间欧几里德方差的均值。方差的标准化过程就是将这些平均误差与其真实COA计算结果的模相除,得到的结果就是平均百分比误差(MPE)。
表4中LocKNN一行显示的是通过使用不同规模特征图中的实体位置训练BP神经网络,再利用KNN方法得到决策方案的过程来获取的ME和MPE值。LocProto行显示的是通过使用不同规模特征图中的实体位置训练BP神经网络,再利用特征原型向量得到决策方案的过程来获取的ME和MPE值;DifKNN一行显示的是通过使用不同规模特征图中实体间位置的差异性训练BP神经网络,再利用KNN方法得到决策方案的过程来获取的ME和MPE值;DifProto一行显示的是通过使用不同规模特征图中实体间位置的差异性训练BP神经网络,再利用特征原型向量得到决策方案的过程来获取的ME和MPE值。
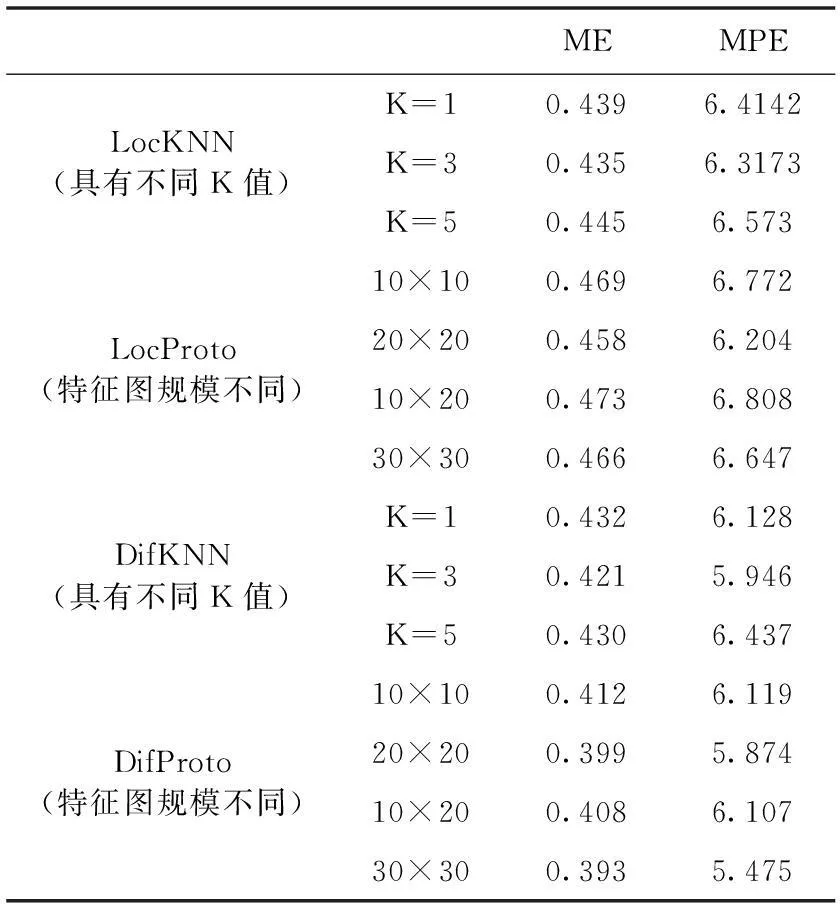
表4 所有方法的试验结果
表5显示了上述所讨论方法的ANOVA结果,其中p-value≤0.05,F≥Fcrit。因此,表4所显示结果的差异性在统计上不明显。
从表4中的计算结果可以看出,采用位置差异性训练BP神经网络,特征图原型获得的结果最好;相反,采用特征图中实体位置训练BP神经网络,KNN算法得到的决策结果最差。这是因为位置间的差异性比单一位置本身含有更多的信息,并且使用位置间差异性进行网络训练也增加了训练样本的大小。此外,使用决策方案中的特征模型向量过程中,必须考虑整个决策空间,而非只考虑其最近邻域。
5结束语
军事应用问题的研究与开发是一个难度程度非常大的工程。由于CBR方法是一种模仿人类思维过程的计算方法,因此,在军事剧情中使用CBR方法模拟COA的决策过程是十分合理的。但是,指挥实体任务规划的决策空间是一个多维空间,并且决策仿真过程中选取的案例不可能穷举所有情况,因此案例的选取具有有限性。针对上述情况,本文提出了一种解决高维案例空间中有限案例之间的适应性问题。首先将问题空间和决策空间分别映射到两种不同的ViSOM中,然后分析这两类映射空间之间的映射关系,最后选取一个简单的军事剧情作为实例进行效果验证,取得了理想的效果。虽然案例数据库中所有的案例属性都具有数值,但是非数值属性也可以先转换为数值再被使用。因此,本文方法可以应用于其他数据库中。但是这项研究只是一个概念论证方面的尝试,对于实际作战过程中的应用效果以及今后研究过程中如何结合相关的能力评估方法真实表示兵力能力的大小等问题还有许多需要改进提高的地方。
表5不同方法的ANOVA结果
ANOVA:单因素

组次数总数平均值误差Lock=1104.390.4398.89E-05Lock=3104.350.4352.22E-05Lock=5104.450.4451.34E-05Loc10×10104.690.4691.34E-08Loc20×20104.580.4582.25E-05Loc10×20104.730.4734.45E-05Loc30×30104.660.4663.53E-08Difk=1104.320.4324.44E-05Difk=3104.210.4212.27E-05Difk=5104.30.431.08E-06Dif10×10104.120.4122.29E-05Dif20×20103.990.3993.21E-05Dif10×20104.080.4088.07E-05Dif30×30103.930.3934.89E-08
ANOVA:总结

产生变动来源SsdfMSFP-valueFcrit组间0.087469130.006728246.48937.45E-831.798584组内部0.0034391262.73E-05总共0.090908139
参考文献:
[1]Leake, B., Kinley, A., Wilson, D. Acquiring case adaptation knowledge: a hybrid approach[C].Proceedings of the Thirteenth National Conference on Artificial Intelligence, AAAI Press, Menlo Park, CA, 1996.
[2]Hanney, K., Keane, M. T. The adaptation knowledge: how to easy it by learning from cases[C].Proceedings of the Second International Conference on Case-Based Reasoning, Springer, Berlin,1997: 359-370
[3]Jarmulark, J., Craw, S., Rowe, R. Using case-base data to learn adaptation knowledge for design[C].Proceedings of the Seventeenth IJCAI Conference, Morgan Kaufmann, San Mateo, CA, 2001: 1011-1016,
[4]Wilke, W., Vollrath, I., Althoff, K.D., Bergmann, R. A framework for learning adaptation knowledge based on knowledge light approaches[C].Proceedings of the Fifth German Workshop on Case-Based Reasoning, 1997.
[5]段美美,于本海,朱荫.基于CBR的软件项目成本估算方法[J].计算机工程与设计,2014,35(11):3837-3844.
[6]李蕾,祁慧敏,杨凤霞.基于案例与模糊推理的中医诊断系统研究[J].信阳师范学院学报(自然科学版),2014,27(4):585-588.
[7]董磊,任章,李清东.基于模型和案例推理的混合故障诊断方法[J].系统工程与电子技术,2012,34(11):2339-2343.
[8]任章,李清东,董磊,等.基于案例推理和等价空间的定性/定量混合诊断故障方法[J].南京航空航天大学学报,2011,43(5):87-90.
[9]Bauer, H.U., Pawelzik, K. R. Quantifying the neighbourhood preservation of self-organizing feature maps[J]. IEEE Transactions on Neural Networks,1992,13(4): 570-579.
[10]Kohonen, T. Self-Organizing Maps. Vol.30 of Springer Series in Information Sciences[M].3rd ed.. Springer-Verlag,Berlin Heidelberg,2001.
[11]Kirk, J. S., Zurada, J.M. A two-stage algorithm for improved topography preservation n self-organizing maps[C]. in: 2000 IEEE International Conference on Systems, Man, and Cybernetics, Vol.4, IEEE Service Center.2000:2527-2532.
[12]Su, M.C., Chang, H.T. A new model of self-organizing neual networks and its application in data projection[J]. IEEE Transactions on Neural Networks,2001,12(1):153-158.
[13]Pratt, D.R. Case based reasoning for the next generation synthetic force[C]. Technical Report SAIC-01/7836&00, Science Applications International Corporation, Orlando, FL, 2001.
书讯
由江苏自动化研究所信息融合团队精心翻译、德国通信信息系统与人机工程研究所Kolfgang Koch博士原著的《跟踪和传感器数据融合》一书于2015年由科学出版社正式出版。该书基于贝叶斯原理对“回溯”与“平滑”之间的异同、雷达分辨率模型、干扰机凹槽建模等进行了系统的研究,并采用相控阵雷达真实数据对相关模型和方法进行了验证。该书将数据融合与传感器/环境等特性视为一个整体进行研究,有理论深度的同时与实际工程紧密结合,对我国从事数据融合和教学的科研人员有很好的启发和指导作用。
High Dimensional Solution Space Adaptation of Command Entity’s Mission Planning Based on Case-Based Reasoning
ZHANG Yuan, QI Yu-dong, QIAO Yong-jun, CHEN Qing-hua
(Naval Aeronautical and Astronautical University, Yantai 264001, China)
Abstract:Adaptation is the most difficult stage in the Case-Based Reasoning cycle, especially, when the solution space is multi-dimensional in the Command Entity’s Mission Planning. This paper discusses the adaptation of a high dimensional solution space in the Command Entity’s Mission Planning and proposes a possible approach to it. A Visualization induced Self Organizing Map is used to map the problem space and solution space first, then a Back Propagation network is applied to analyze the relations between these two maps. A simple military scenario is used as a case study for evaluation purposes.
Key words:CBR; multi-dimensional solution space; Adaptation; Visualization induced Self Organizing Map; mission planning
作者简介:张媛(1982-),女,山东蓬莱人,博士研究生,研究方向为智能决策、指挥信息系统。
*基金项目:国家自然科学基金(6150488)
收稿日期:2015-09-19
中图分类号:E94
文献标志码:A
DOI:10.3969/j.issn.1673-3819.2016.01.007
文章编号:1673-3819(2016)01-0028-06

