基于切换增益变结构控制的导弹自动驾驶仪设计*
赵艳辉,闫 亮,张公平
(中国空空导弹研究院控制所,河南洛阳 471009)
基于切换增益变结构控制的导弹自动驾驶仪设计*
赵艳辉,闫 亮,张公平
(中国空空导弹研究院控制所,河南洛阳 471009)
为了提高经典三回路自动驾驶仪的性能,对采用尾舵控制的弹体对象设计了切换增益变结构控制自动驾驶仪。采用切换增益变结构控制的闭环响应特性对弹体参数的变化不敏感。控制量是光滑的避免了对执行机构有害的频繁切换。采用增益调度技术可以容易的获得全空域的控制器设计。仿真结果表明了设计方法的有效性。
自动驾驶仪;变结构控制;切换增益;飞行控制系统
0 引言
三回路驾驶仪凭借其简单的控制结构和优良特性,在战术导弹控制中得到广泛的应用。文献[1]给出了多种可能的三回路驾驶仪结构,并对不同的控制结构进行了鲁棒性分析。文献[2]给出了中环为伪攻角反馈的三回路驾驶仪结构,讨论了舵机带宽、非最小相位零点、弹体一弯频率以及有限控制量约束条件下的三回路快速性极限问题;文献[3]通过固定混合比例假设,将被控对象等价为单输入系统,并设计了两回路变结构控制器,但对具有一定静不稳定水平的弹体稳定性下降。文献[4]采用积分变结构控制方法设计了侧向过载控制器,并采用边界层函数削弱了控制量的抖振问题,但控制参数的确定过程十分繁琐。
文中以尾舵控制的空空导弹俯仰动力学特性为被控对象,在经典三回路驾驶仪设计的基础上设计了变增益变结构控制器。该控制系统继承了三回路控制结构,可与增益调度控制算法相结合,工程上易于实现;在弹体参数摄动的情况下,相比于经典三回路驾驶仪提高了加速度响应的动态品质。
1 被控对象的数学模型
三回路自动驾驶仪的基础设计是基于被控对象的小扰动线性化和线性系统控制理论开展的。俯仰通道弹体传递函数如下:
(1)
角速度到攻角的传递函数可近似为:
角速度到加速度的传递函数可近似为:
非最小相位零点:
其中:a1、a2、a3、a4、a5为常用的动力学参数[5]。
δp为俯仰通道舵偏;V为导弹速度;ay为俯仰通道测量加速度;ωz为俯仰角速度;α为攻角。
关于控制量的符号作如下约定:正的气动舵偏产生负的操纵力矩。
2 控制器设计
该变增益变结构自动驾驶仪设计的思路是:首先设计伪攻角三回路驾驶仪,确定阻尼回路控制增益和伪攻角回路的控制增益;其次在线性控制的基础上对加速度反馈回路施加切换增益变结构控制,通过设计合理的切换函数,实现加速度误差积分控制增益的切换。变增益变结构自动驾驶仪原理图如图1所示。图中:Kω为阻尼回路增益;Kα为伪攻角回路增益;Kei为误差积分增益;Ke为误差比例增益。
2.1 线性控制器设计
经典三回路驾驶仪通常采用极点配置的方法进行设计。俯仰通道加速度闭环传递函数如下:
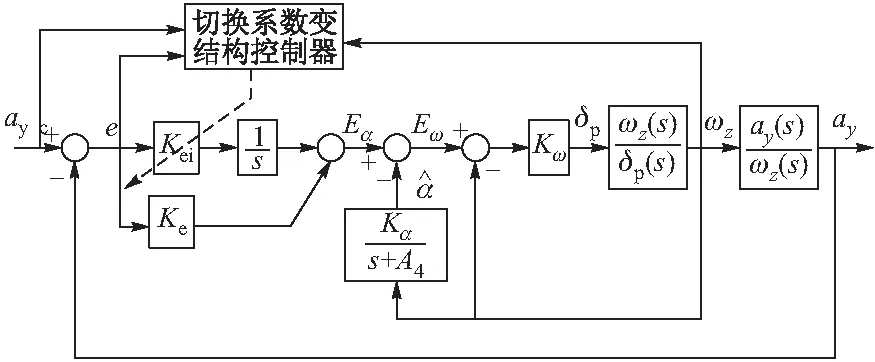
图1 变增益变结构自动驾驶仪原理图
(2)
式中:
B2=(-Kωa3+a1+a4)
设期望的闭环特征多项式为:
(s+A)(s2+2ζωs+ω2)
则有如下关系成立:
俯仰通道开环传递函数如下:
通过中频段近似可知:
Kω(-a3)=ωcr
综合考虑舵机带宽、非最小相位零点、一弯弹性振荡频率的约束,在确定系统开环带宽和闭环阻尼比的情况下,确定闭环传函的零极点分布,可得使等效一阶时间常数极小化的一组线性控制增益。典型的闭环零极点分布图如图2所示。
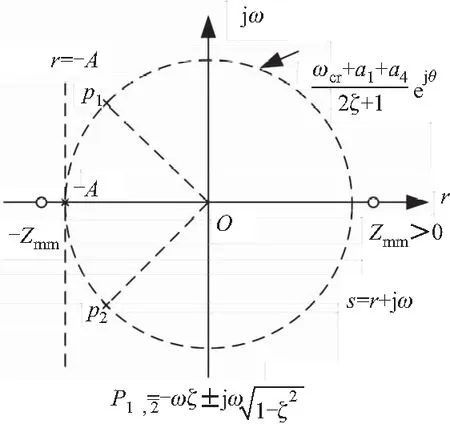
图2 使等效一阶时间常数极小化的闭环零极点分布图
2.2 变结构控制器设计
阻尼回路和伪攻角回路控制增益的引入改善了弹体二阶极点对的阻尼比和稳定性,使得由Eα到ωz的传递特性稳定并具有良好的阻尼比。引入状态反馈后的等效控制框图如图3所示。
其中:
b=KωV(a2a5-a3a4)>0
τ2=(a1+a4-Kωa3)>0
τ1=a2+a1a4+Kω(a2a5-a3a4)+KαKω(-a3)>0

图3 引入状态反馈后的等效加速度控制框图
控制关系为误差比例积分控制:
误差定义:e=ayc-ay
其中:c2>0,c1>0。
考虑阶跃输入的情况下,切换面函数的变化为:
将动态约束方程代入上式得:
令Ke=(c1-τ1-(c2-τ2)c2)/b
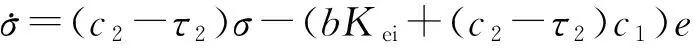
PA6粒子以及自制的PAPP在使用前均在100 °C烘箱中干燥12 h。随后将PAPP和PA6按照不同的比例混合,加入密炼机中。每次加料70 g,转子转速为40 转/min,密炼温度为230 °C,密炼时间为10 min。将所得样品在平板硫化机压板成型,模压温度为240 °C,模压时间为10 min。最后按照测试需要制备成标准样条,测试结果取5次测试结果的平均值。各组分比例见表1。
选择Lyapunov函数:V(σ)=σ2/2
Lyapunov函数的变化率为:

进一步有:
式中:
为避免引入正实零点,限制Ke≥0。
至此得到了积分控制增益的切换条件,再看切换面函数的具体形式。由简化的角速度到加速度的传递函数可得如下微分方程:
结合误差定义方程将误差的各阶导数代入切换面函数表达式,得到:
σeq=e-K6yωsynth
ωss=ac/V
k为设定数,它和(c2-1/Tm)k一起决定了稳态时角速度收敛的快慢程度。
在切换面函数中存在角加速度信号,为了避免微分角速度信号带来的测量噪声放大问题,采用滤波器对角速度和角加速度进行估计,原理如图4所示,其中p为滤波器带宽。
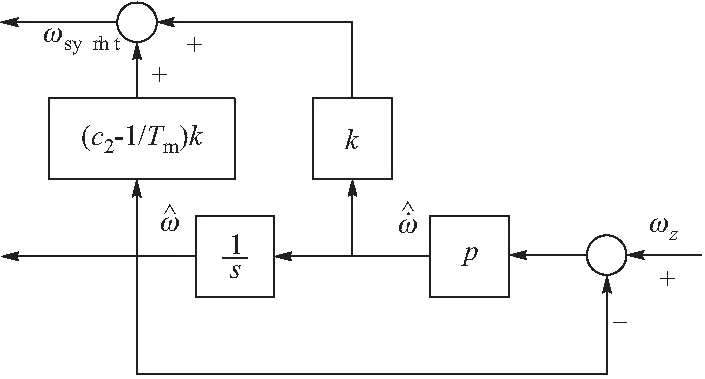
图4 通过滤波器估计角加速度和角速度信号
下面讨论切换面运动特征方程参数的选择。
1)依据期望的角速度误差运动规律确定k,(c2-1/Tm)k;
2)由(c2-1/Tm)k确定c2,并注意稳定性条件要求c2<τ2,由开环系统穿越频率表达式可知τ2=(a1+a4-Kωa3)≈a1+a4+ωcr,则c2有较大的选择空间;
则最终的加速度误差积分控制增益切换逻辑为:
(3)
式中:
σeq=e-K6yωsynth
3 仿真验证
以高度10 km,马赫数2的特征点为例,进行线性控制器和变结构控制器的设计。

表1 被控对象标称参数

表2 线性控制增益

表3 和变结构控制有关的控制参数
积分控制增益切换逻辑:
式中:Kei,nom=0.166;c+=1.1,c-=0.7。
给定相同的加速度指令,对标称参数和参数摄动情况下的仿真结果进行对比分析,参数摄动主要考虑静稳定度随攻角的变化,a2的变化范围为标称值的±5倍,覆盖一定的静稳定和静不稳定区域。仿真结果如图5~图9所示。

图5 加速度响应曲线对比

图6 角速度响应曲线对比

图7 控制量对比曲线
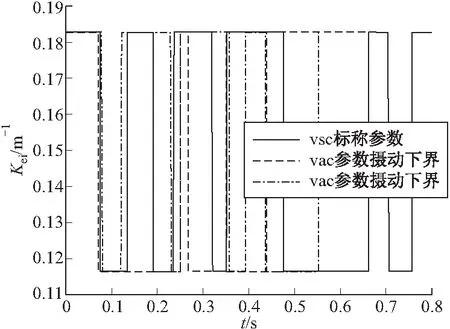
图8 控制增益切换曲线
图5~图6的加速度和角速度响应曲线表明:采用变结构控制器的加速度响应一阶等效时间常数和线性控制器的差异小于5 ms,切换增益变结构控制使加速度响应对参数变化不敏感,超调量较小,改善了闭环响应特性;仿真同时表明忽略非最小相位特性的切换面函数设计是可行的。

图9 切换面函数对比曲线
图7~图8的控制量和加速度误差积分控制增益曲线表明:控制增益的切换并未造成控制量的频繁抖动,体现了切换增益变结构控制的优点。
图9中的切换面函数曲线表明:在有限的过渡过程时间内切换面函数收敛于0,系统进入稳态,满足一类战术导弹驾驶仪的使用需求。
4 结论
文中采用切换增益变结构控制方法提高了经典三回路自动驾驶仪的性能,系统闭环响应对参数变化不敏感,增益切换并未造成控制量的频繁切换。采用增益调度技术可以很方便实现全空域的控制器设计,贴近工程实际需求。仿真结果表明了设计方法的正确性和控制器的有效性。
[1] MRACEK C P, RIDGELY D B. Missile longitudinal autopilot: comparison of multiple three loop topologies [C]∥ AIAA Guidance, Navigation, and Control Conference and Exhibit, 2005.
[2] 李友年, 郑鹍鹏, 陈星阳. 三回路过载驾驶仪的快速性极限分析 [J]. 弹箭与制导学报, 2013, 33(3): 17-20.
[3] 李友年, 贾晓洪. 一种直接力/气动力复合控制自动驾驶仪的设计方法 [J]. 弹箭与制导学报, 2005, 25(2): 1-3.
[4] 张记华, 张春明, 刘剑锋. 防空导弹侧向姿态变结构控制器研究 [J]. 上海航天, 2005(4): 23-26.
[5] SIOURIS G M. Missile guidance and control system [M]. NewYork: Springer-Verlag, 2004: 137-140.
[6] 朱敬举, 祁载康, 夏群力. 变结构控制方法及其在导弹驾驶仪设计中的应用问题 [J]. 飞航导弹, 2007(2): 30-33.
Missile Autopilot Design Based on Switching-gain Variable Structure Control
ZHAO Yanhui,YAN Liang,ZHANG Gongping
(System Control Institute, China Airborne Missile Academy, Henan Luoyang 471009, China)
A pitch plane switching-gain variable structure autopilot was designed for a missile controlled by aero tails to improve the performance of classical three-loop autopilot. The close-loop response is insensitive to parameter variation of missile body by applying switching-gain variable structure methodology. The control signal is smooth without high-frequency oscillation which is disadvantageous for actuators. The controllers for all flight envelopes can be easily achieved when gain-scheduling is used. The simulation result shows that the design method is valid.
autopilot; variable structure control; switching gain; flight control system
2015-09-12
赵艳辉(1982-),男,河北围场人,工程师,研究方向:空空导弹自动驾驶仪设计与仿真。
TJ76
A

