基于最小最大模块化集成特征选择的改进

周 丰，王未央

(上海海事大学信息工程学院，上海 201306)

基于最小最大模块化集成特征选择的改进

周 丰，王未央

(上海海事大学信息工程学院，上海 201306)

随着数据规模的扩大，单个弱分类器的准确率已经无法很好地对未知样本进行预测，为此提出了集成学习。在集成学习与分类器结合的同时，集成的思想同样被用到了特征选择中。从提高对样本预测的准确率的角度出发，提出一种基于最小最大模块化(Min-Max-Module，M3)的策略。它同时将集成学习应用到了特征选择算法和分类器中，并对比了四种集成策略以及三种不同的分类方法。结果表明，提出的方法在大多情况下能取得不错的效果，并且能很好地处理不平衡的数据集。

特征选择;集成学习;最小最大模块化策略;不平衡数据

1 概述

随着各个领域涌现出的大量数据，机器学习与数据挖掘已经被应用到各行各业。但是现实生活中的数据非常复杂，平滑干净的数据非常难得，大部分的数据中都有缺失值、异常值等噪声。此时，数据预处理显得格外重要。为了提高机器对这些数据的处理能力，可以通过一定的数学方法(如牛顿插值法、拉格朗日插值法等)进行处理，而特征选择作为降低数据维度、平滑噪声的一种有效方法，成为了研究热点［1］。

在数据挖掘中，海量的原始数据中存在着大量不完整、不一致、有异常的数据，它们会严重影响到数据挖掘建模的执行效率，所以数据清洗尤为重要。数据清洗主要是删除原始数据集中的无关数据、重复数据、平滑噪声数据，筛选掉与挖掘主题无关的数据，处理缺失值、异常值等［2］。处理缺失值和异常值，通常有删除记录、数据插补和不处理等方法，而异常值一旦被检测到，往往可以当作缺失值处理。常用的方法有均值/众数/中位数插补法、固定值法、最近邻插补、回归方法以及插值法。插值法一般有拉格朗日插值法和牛顿插值法，文中使用牛顿插值法。箱型图分析提供了识别异常值的标准:异常值通常被定义为小于QL-1.5IRQ或大于QU+1.5IRQ的值。其中，QL为下四分位数; QU为上四分位数;IRQ为四分位数间距，IRQ=QU-QL。

特征选择是从特征集合中挑选出满足一定评价准则的特征子集的过程，特征选择过程可以除去不相关的冗余特征［1-2］，从而达到降维的目的。特征选择算法一般分为四类:过滤器、封装器、嵌入式和组合。过滤器最大的特点是直接从特征固有的性质出发来评判特征的重要性，并不考虑分类器，该类方法具有较高的效率，如Fisher［3］、Relief［4］等。封装器则是依赖于分类器，它采用分类器来评价性能，这种方法采用搜索策略来寻找最优特征子集，其搜索策略有前向搜索、后向搜索、随机搜索等，准确率较高但是效率较低。嵌入式则是在构建分类器的过程中进行特征选择。而组合式先采用过滤器去除一些特征，再对剩下的特征子集采用封装器进行搜索，结合了过滤器和封装器的优点。

目前，数据量在不断增长，传统的特征选择方法的效率显然已经无法跟上数据增长的脚步［1］。为了更好地处理大规模数据，Hoi［5］等结合在线特征选择和一种嵌入式算法，将原始数据转换为序列型的数据;Wu［6］等使用在线流式特征选择的方法。以上两种方法都能明显地提升对大规模数据的处理能力。

文中使用的是集成的方法，主要步骤包括:结合箱型图分析和牛顿插值法对数据进行缺失值和异常值分析;再通过某种策略将数据划分，从而将原始特征选择和分类任务划分为多个较小的相互独立的可并行计算的子任务，每一个子任务同时进行特征选择以及分类算法;最后利用最小最大策略将分类结果进行集成。

2 集成学习

2.1 集成学习的概念与框架

与传统的单个学习模型相比，集成学习则是通过同时构建多个不同的基学习模型，并使用某种策略把多个模型的学习结果进行组合，从而获得最终的学习结果。

此外，集成思想与特征选择相结合，用以提高特征选择的稳定性［2，7-9］。大量的理论研究和实际应用表明，集成学习有利于构建性能更好的学习模型。集成学习在分类问题中大致分为两个步骤。首先，根据数据集训练出多个不同的分类器;然后，将未知数据在不同分类器上的预测结果通过某种策略进行汇总，整合成最终的预测结果。汇总的策略有投票法、权重法、聚类法等。

常见的集成策略有以下几种，如 Bagging、Ada-Boost、M3、RandomSpace等。该实验使用基于M3的集成策略对结果进行集成，特征选择算法使用了Fisher 与ReliefF;分类算法使用经典的、准确率较高的支持向量机，并与单个支持向量机分类器和朴素贝叶斯三者之间进行比较。

2.2 集成的策略

在每个子任务结束后，需要将每个任务的结果以某种方法集成起来，文中将介绍与对比四个集成的策略:均值法、投票法、K-中心聚类法以及最小最大集成策略。此处主要介绍前三种:

投票法对于特征选择而言是先将结果转换为特征子集，然后统计每个特征被选中的情况，将出现次数最多的M个特征作为最终输出特征;同理对于分类而言则是统计每一个子分类器对同一个样本预测的结果，取票数最高的作为输出;

均值法将子任务返回的结果进行线性相加取均值得到最后的输出;

K-中心聚类集成是应用了聚类的思想，从多个子任务中选择具有代表性的结果作为输出。相比前两种方法，该方法可以保护特征之间的关联性。文中采用了1-中心聚类集成。

3 最小最大集成策略

基于最小最大模块化(Min-Max-Module，M3)的分类集成策略最早由Lu［10］等提出。该策略主要包含两个步骤:任务分解和分类结果的合成。

3.1 任务分解

在任务分解阶段，对于一个K类的分解问题，首先采用“一对一”的策略将其分解为K(K-1)/2个二分类问题。假设K类的训练数据集表示为:其中，Li表示第i类样本的个数;xil表示第i类样本中的第l个样本;yi表示第i类样本对应的标签。

那么通过“一对一”的策略，第i类样本和第j类样本组成的二分类问题的训练数据集可以表示为:

如果二分类问题的规模较大或者具有不平衡性，可以进一步将它们划分成规模更小的较为平衡的子问题。

任务分解方法包括基于随机的分解方法和基于超平面的分解方法。该实验中使用基于超平面的方法，其具体过程如算法1所示。假设把Ci类的训练样本分解成Ni个子集，把Cj类的训练样本分解成Nj个子集。这样就可以把Ci类和Cj类的二分类问题分解成Ni×Nj个子二分类问题进行解决［11］。

算法1:基于超平面的数据集分块方法。

输入:某k类问题第i类的训练样本Xi，i=1，2，…，k。

(1)计算Ci类的每个训练样本x与超平面Z1+Z2+…+Zn=0的距离。

其中，xj，j=1，2，…，n是样本x的分量。

(2)根据已经计算的dist(x，H)的值，对Ci类的训练样本进行排序，即把Ci类的训练样本按空间分布进行排序。

(3)把已经排序的训练样本按前后顺序划分成Ni份，每一份的训练样本个数近似相等(相差不超过一个)，即把该类训练样本的分布空间分割成Ni个部分，但不是分割后的空间相等，而是保证各个部分空间中包含的样本个数相等。

3.2 分类结果集成

通过对第i类样本和第j类样本组成的二分类问题进行进一步的划分，从而得到Ni×Nj个二分类子问题，然后在每个子问题对应的训练数据集上训练相应的分类器，得到Ni×Nj个基分类器，表示为:

对于测试样本，使用这些基分类器分别对其进行预测，得到预测标签:

对于预测结果，分别采用最小规则和最大规则进行合成:

MIN规则:是对拥有相同正类训练样本集和不同负类训练样本集的分类结果取最小值;

MAX规则:是对拥有相同负类训练样本集和不同正类训练样本集的分类结果取最大值。

该分类集成策略的整体流程如下:

算法2:基于最小最大规则的集成算法。

输入:训练集X，测试样本e，第i类样本的划分块数Ni，数据划分方法P;

输出:测试样本的预测标签O。

训练与测试阶段:

将K类样本X划分为X1，X2，…，Xk

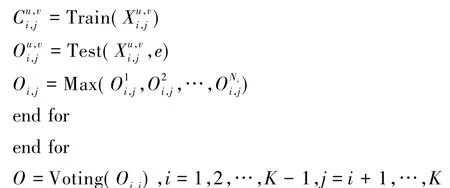
3.3 最小最大策略的集成特征选择以及分类

传统的基于最小最大策略的分类是先将数据集进行特征选择等预处理，再利用上文提到的数据划分方法将数据划分为M×N个样本子集，再将数据块进行合并分类，对每一个样本都有M×N个预测标签，再利用最大最小策略可以得到每一个样本最终的预测标签作为输出［12］。

传统的基于最小最大策略的集成特征选择则是先使用上文提到的数据划分方法进行数据划分，得到M ×N个样本子集，然后在每个样本子集上进行特征选择，得到M×N个特征选择结果。最后利用最小化集成单元和最大化集成单元对这多个特征选择结果进行组合［12-15］。

文中提出的方法是结合以上两种传统的集成方法，将特征选择和分类同时使用最小最大模块化进行集成，先进行数据分块，对每一个数据子集进行特征选择，并优先对特征选择集成。同时，保存划分的数据子集，在得到最优特征子集之后，更新数据子集并对新的数据子集进行分类集成，从而得到最后的结果。其过程如图1所示。

图1 基于最小最大规则集成分类特征选择的框架

4 实验及仿真

4.1 实验步骤

文中所做的相关工作及实验步骤为:

(1)对原始数据做箱型图处理，寻找异常值并删除，再将排除完异常值的数据集运用牛顿插值法(完成异常值和缺失值的处理过程具体见算法1)。

(2)接下来对数据进行标准化、归一化处理，区间为［0，1］。

(3)对处理好的数据进行十字交叉验证或者直接进行训练集和测试集的按比例划分。

(4)对训练样本和测试样本分别使用基于超平面的方法得到若干较小数据子集，对每个数据子集使用相同的特征选择算法，得到降维之后的数据。

(5)用降维之后的数据更新之前的数据子集，并对每个数据子集使用支持向量机算法进行分类。

(6)根据最小最大规则对分类结果进行集成得到最终输出。

本节通过实验结合了基于最小最大策略的分类算法和特征选择算法，分别对比ReliefF和Fisher特征选择算法、投票法、均值法、K-中心聚类法以及最小最大策略对分类准确率的影响。在集成方面，将文中提出的方法与传统的M3-SVM和M3-Naïve Bayes方法进行对比。实验数据集为PCMAC和Adult。

4.2 实验准备

(1)实验数据集。

PCMAC数据集包含1 943条样本，每条样本有3 290维属性，包含了若干异常值和缺失值，标签一共有两类，是一个低数据量高维的样本。文中对其进行十字交叉验证，得到训练样本和测试样本。该数据集具体的分布情况如表1所示。

Adult数据集包含32 561条样本，124维属性，同时包含了异常值和缺失值，一共有两类标签。文中训练集包含22 696条样本，测试集9 865条样本，具体分布如表2和表3所示。

需要说明的是，由于M3希望尽可能地保持每个子数据块的样本数相似，故对M3的分块个数需要针对样本个数区分，这样也能很好地处理不平衡数据集。

(2)分类器的选择及评价准则。

文中采用的分类器算法是支持向量机。支持向量机有良好的学习能力和泛化能力，主要思想是:对于样本的输入空间，构造一个最优的超平面，使得超平面到两类样本之间的距离最大化。它遵循结构风险最小化的原则，使得错误概率上界最小化，因此还可以有效减小过拟合。在支持向量机中，文中采用高斯核函数，其Sigmod值设置为2，损失函数C设置为32，采用SMO算法计算其参数。

对于分类结果的评价采用错误率度量标准，但是错误率不考虑类别之间的不平衡。对于平衡数据，常采用准确率或错误率来衡量;对于不平衡数据，常采用的评价标准包括ROC曲线、AUC、F-Measure和GMean等。文中采用G-Mean。

其中，TP表示正类样本被正确分类的个数;FN表示正类样本被错误分类的个数;TN表示负类样本被正确分类的个数;FP表示负类样本被错误分类的个数。

4.3 实验结果

4.3.1 在PCMAC数据集上的实验结果

该数据集样本数较少，维数较高，且为平衡数据集，在该样本上使用了Fisher特征选择算法。

(1)使用ReliefF特征选择算法。

基于超平面划分数据后，对每一个数据子集使用Fisher特征选择算法后使用SVM作为分类器，分别采用四种不同的集成策略以G-Mean为标准进行对比，如图2所示。

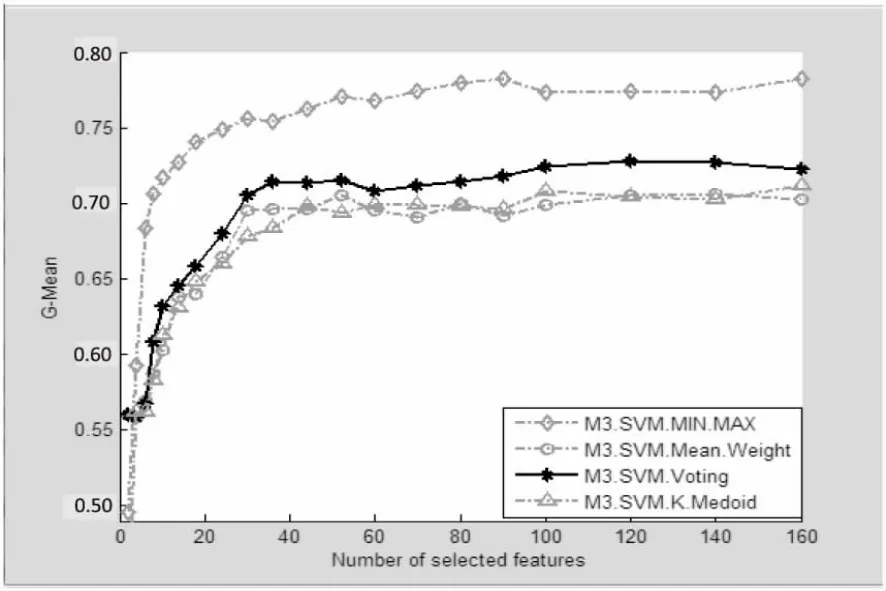
图2 不同集成策略对比图(1)

对文中提出的集成特征选择(FSE)结合集成分类(CFE)与传统的FSE进行对比，并通过传统的FSE对比了SVM和NB两个分类器的效果，如图3所示。

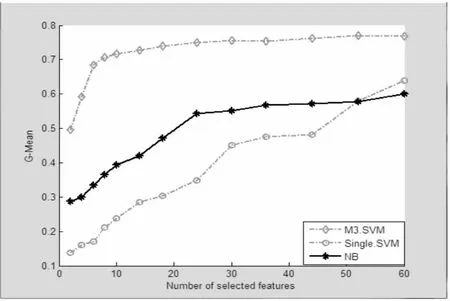
图3 集成算法与单个算法对比图(1)

4.3.2 在Adult数据集上的实验结果

该数据集样本数较多，且不平衡，属性个数较少，此处仅采用了ReliefF特征选择算法，同样对比了文中提出的FSE+CFE与传统的集成特征选择，实验结果如图4和图5所示。

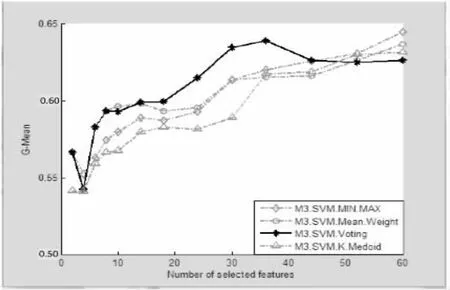
图4 不同集成策略对比图(2)

4.3.3 实验结果分析

实验主要对比了四种集成策略:均值法、投票法、K-中心聚类法以及基于最小最大策略(分别记为Mean.Weight、Voting、K.Medoid、MIN.MAX)。并对比了三种不同的分类方法:基于最小最大策略的集成特征选择与集成分类结合方法、传统的集成特征选择结合SVM、传统的集成特征选择结合朴素贝叶斯(分别记为M3.SVM、SVM、NB)。数据划分部分使用了超平面划分，特征选择算法使用了ReliefF和Fisher，使用GMean作为评价准则。实验数据集使用PCMAC和A-dult，前者样本较少、特征较多，故采用10次交叉验证。

根据实验结果，在样本较少特征较多的PCMAC中，文中提出的M3-FS结合M3-SVM的效果明显优于其他集成策略和分类方法，特别是选取60至80维特征。对于大量低维的样本Adult，由图4、图5可见，四种集成策略具有相似的结果及趋势;在分类器选择方面，文中提出的M3-FS结合M3-SVM的效果优于M3-FS结合SVM以及M3-FS结合NB。同时可以看出，使用M3的正负类样本分别分块策略也能很好地处理Adult这个不平衡的数据集。

综上所述，从分类准确率的角度，文中提出的方法在大部分情况下均优于其他方法。

5 结束语

文中提出了一种对传统的集成特征选择方法加以改进的方法，即将分类集成与特征选择的集成结合起来，以有效地提高对大规模数据的处理能力。该方法通过基于超平面的方法将数据划分成多个数据子集，将原来的任务转换为可同时进行的多个独立的子任务，然后使用最小最大集成单元对分类结果进行集成，得到最终的预测标签。通过比较，实验结果表明在四种集成策略中，最小最大集成策略是占有一定的优势的。在面对传统的特征选择集成方法中，在准确率方面，结合分类集成的方法的效果更为理想。

［1］ Tang J L，Alelyani S，Liu H.Feature selection for classification:a review［M］.Florida:The Chemical Rubber Company Press，2013.

［2］ Li Y，Gao S，Chen S.Ensemble feature weighting based on local learning and diversity［C］//Proc of AAAI conference on artificial intelligence.［s.l.］:［s.n.］，2012.

［3］ Gu Q，Li Z，Han J.Generalized fisher score for feature selection［C］//Proceedings of the twenty-seventh conference on uncertainty in artificial intelligence.Barcelona，Spain:［s.n.］，2011.

［4］ Robnik-Šikonja M，Kononenko I.Theoretical and empirical analysis of ReliefF and RReliefF［J］.Machine Learning，2003，53(1-2):23-69.

［5］ Hoi S C H，Wang J，Zhao P，et al.Online feature selection for mining big data［C］//Proc of international workshop on big data，streams and heterogeneous source mining:algorithms，systems，programming models and applications.［s.l.］:ACM，2012:93-100.

［6］ Wu X，Yu K，Wang H，et al.Online streaming feature selection ［C］//Proc of international conference on machine learning. ［s.l.］:［s.n.］，2010:1159-1166.

［7］ Woznica A，Nguyen P，Kalousis A.Model mining for robustfeature selection［C］//Proc of ACM SIGKDD conference on knowledge discovery and data mining.［s.l.］:ACM，2012:913 -921.

［8］ Awada W，Khoshgoftaar T M，Dittman D，et al.A review of the stability of feature selection techniques for bioinformatics data ［C］//Proc of international conference on information reuse and integration.［s.l.］:［s.n.］，2012:356-363.

［9］ 季 薇，李 云.基于局部能量的集成特征选择［J］.南京大学学报:自然科学版，2012，48(4):499-503.

［10］ Lu B L，Ito M.Task decomposition and module combination

based on class relations:a modular neural network for pattern classification［J］.IEEE Transactions on Neural Networks，1999，10(5):1244-1256.

［11］周国静，李 云.基于最小最大策略的集成特征选择［J］.南京大学学报:自然科学版，2014，50(4):457-465.

［12］陈晓明.海量高维数据下分布式特征选择算法的研究与应用［J］.科技通报，2013，29(8):79-81.

［13］连惠城.最小最大模块化网络及人脸属性分类研究［D］.上海:上海交通大学，2008.

［14］解男男.机器学习方法在入侵检测中的应用研究［D］.长春:吉林大学，2015.

［15］闫国虹.支持向量机不平衡问题和增量问题算法研究［D］.西安:西安电子科技大学，2012.

Improvement of Multi-classification Integrated Selection Based on Min-Max-Module

ZHOU Feng，WANG Wei-yang
(School of Information＆Engineering，Shanghai Maritime University，Shanghai 201306，China)

With the expansion of the data size，a single weak classifier has been unable to predict unknown samples accurately.To solve this problem，an integrated learning is proposed.Combined the integrated learning and classification，the idea of integration is also used in the feature selection at the same time.For the increase of sample prediction accuracy，a strategy based on Min-Max-Module(M3)is put forward.It makes integrated learning applied to feature selection algorithms and classifier，and compares four kinds of integration strategies as well as three different classification methods.The results show that the proposed method can be able to achieve good results in most cases，and can well handle imbalanced data sets.

feature selection;integrated learning;Min-Max-Module(M3);Imbalance Data Sets(IDS)

TP391

A

1673-629X(2016)09-0149-05

10.3969/j.issn.1673-629X.2016.09.033

2015-09-17

2016-01-06< class="emphasis_bold">网络出版时间:2

时间:2016-08-23

国家自然科学基金青年项目(61303100)

周 丰(1991-)，女，硕士研究生，研究方向为挖掘算法中的特征处理;王未央，硕士生导师，研究方向为数据库系统、系统与数据整合、数据挖掘及其在港航、海洋、物流信息系统中的应用。

http://www.cnki.net/kcms/detail/61.1450.TP.20160823.1343.032.html