下承式简支梁拱组合桥梁静载试验工况研究
史 杰,王荣波
(1. 浙江浙交检测有限公司, 杭州 310015;2. 中国市政工程华北设计研究总院有限公司成都分公司, 成都 610031)
下承式简支梁拱组合桥梁静载试验工况研究
史 杰1,王荣波2
(1. 浙江浙交检测有限公司, 杭州 310015;2. 中国市政工程华北设计研究总院有限公司成都分公司, 成都 610031)
分析了下承式简支梁拱组合桥梁的基本受力特性,确定结构抗力主要影响参数。根据26座已建或在建下承式简支梁拱组合桥的设计数据, 分析拱梁刚度比与拱肋抗弯刚度间,拱肋、系梁截面抗弯刚度与轴向刚度间,以及拱肋抗弯刚度与吊杆轴向刚度的变化规律,拟合出各参数之间相关方程。依此设计出一组具有相同计算跨径、设计荷载,不同拱梁刚度比的桥梁模型。利用有限元分析程序,分析该组桥梁主要构件的弯矩、轴力及挠度变化规律,确定其受力最不利截面,得出该类桥梁静载试验的推荐工况。
桥梁工程;梁拱组合桥;有限元分析;静载试验;试验工况
0 引 言
下承式简支梁拱组合桥是一种组合体系桥梁,将梁和拱两种基本结构组合起来,共同承受荷载,充分发挥梁受弯、拱受压的结构特性及其组合作用,达到节省材料的目的。该类桥梁是无推力拱式组合体系桥,为外部静定结构,兼有拱桥较大跨越能力和简支梁桥对地基适应力强的两大特点[1]。该类桥型因其外形美观以及结构受力合理的优点,在江浙地区得到大量的应用。
新建桥梁的交竣工验收及老桥的承载能力评定,一般都要求进行静载试验。桥梁静载试验是测量桥梁结构在静力试验荷载作用下的变形和应力(应变)变化情况,是了解结构实际工作性能(结构刚度、强度)最直接有效的方法。目前相关规范[2-3]中仅对一般类型的拱桥或梁桥静载试验工况进行了规定,对组合体系拱桥尚无明确的规定。目前已有对具体某一座下承式简支梁拱组合桥梁的荷载试验研究[4-5],但没有系统的对该类桥梁荷载试验工况的研究。本文通过对浙江、江苏等地区多座已建或在建的下承式简支梁拱组合桥的资料进行分析,得出主要构件相关设计参数的统计规律,设计出一组可反映该类桥梁受力特点的模型,对其进行汽车荷载作用下的结构效应分析,确定结构的控制截面,得出该类桥梁静载试验的推荐工况。
1 基本受力图示
下承式简支梁拱组合桥主要构件示意如图1,主要由拱肋、系梁、吊杆、横梁(未示出)以及支座构成。
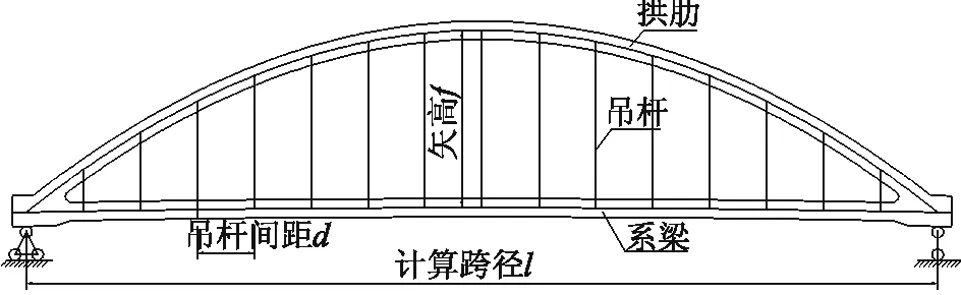
图1 下承载简支梁拱组合桥主要构件示意图
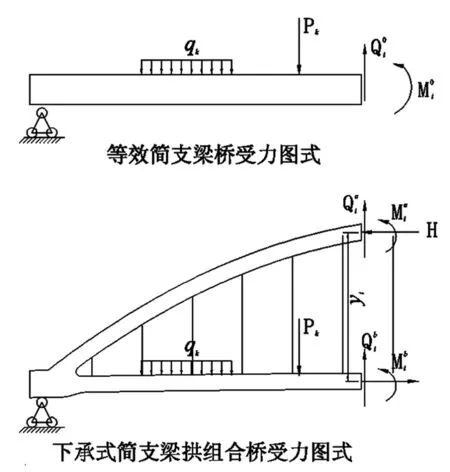
图2 结构受力示意图
当不考虑结构的横向布置,对一片拱肋、系梁进行受力分析时,可比照等效简支梁桥进行[6]。在荷载作用下,任意截面i处的受力示意如图2,截面弯矩可写成式(1)。
(1)

由式(1)可知,下承式简支梁拱组合桥梁抗力由拱肋、系梁以及由拱肋、系梁轴向刚度构成的抗弯刚度三部分组成。在相关参考文献[7-8]中,一般均忽略轴向刚度。研究抗弯刚度对梁拱组合桥内力分配的影响,忽略轴向刚度做参数敏感性分析是可以的,但依此指导实桥的静载试验工况的设置则不够合理。
2 统计资料分析
本文收集了26座桥梁,跨度在50~100m间,矢跨比一般为1/5,个别桥梁为1/4,拱梁刚度比ω在0.07~1.03之间,均属于刚梁刚拱。
通过对桥梁的拱肋、系梁、吊杆等主要构件刚度进行统计分析,拟合出拱梁刚度比ω与拱肋抗弯刚度间,拱肋、系梁抗弯刚度与其轴向刚度间,拱肋抗弯刚度与吊杆轴向刚度间的关系曲线。
由于统计分析的目的是得到合适模型参数,而不是寻找最优的构造尺寸,因此在以下各数据的关系拟合中,不严格控制参数相关性。
2.1 拱梁刚度比与拱肋抗弯刚度关系
由于各桥跨度、宽度、设计荷载并不完全一致。利用相似理论对其进行归一化处理:即拱、梁在弯矩作用下的截面曲率保持不变,利用相似常数将各桥设计参数换算成同跨径、同荷载的桥梁模型。
根据定律分析法[9],可导出相似指标方程:
(2)
式中:Ck、CF、Cl、C(EI)分别为截面曲率、荷载(以集中力表示)、计算跨径及抗弯刚度相似常数。
将各桥归一化处理:计算跨径为1,在单车道(行车道净宽按3.5m计算),公路II级作用下,即有相似常数:
Ck=1,CF=n(n为设计车道数),Cl=l。
由式(2)变换形式有:
(3)
图3为对拱肋抗弯刚度归一化后,拱梁刚度比与拱肋抗弯刚度分布情况。采用二次抛物线拟合可得到拱肋抗弯刚度与拱梁刚度比ω关系式:
(4)

图3 拱肋抗弯刚度与拱梁刚度比拟合曲线图
2.2 拱肋抗弯刚度与轴向刚度关系
统计的桥梁中,拱肋材料为钢管混凝土或钢筋混凝土。钢管混凝土截面包括横、竖哑铃形,横、竖圆端形,倒三角形及单圆管形;钢筋混凝土主要为矩形和工字形。图4为拱肋抗弯刚度与轴向刚度分布情况,线形拟合得到:
(EA)拱=2.1158(EI)拱+26.0219×109
(5)

图4 拱肋抗弯刚度与轴向刚度拟合曲线图
2.3 系梁抗弯刚度与轴向刚度关系
统计的桥梁中,系梁材料均为混凝土。截面形式包括箱形、工字形及矩形。图5为系梁抗弯刚度与轴向刚度分布情况,线形拟合得到:
(EA)梁=1.2920(EI)梁+36.6335×109
(6)

图5 系梁抗弯刚度与轴向刚度拟合曲线图
2.4 拱肋抗弯刚度与吊杆轴向刚度关系
式(1)中虽未体现吊杆轴向刚度对结构抗力的影响,但拱肋分担荷载是由吊杆传递的。传力途径表明吊杆刚度对结构受力也存在影响[10]。假定吊杆的布置满足膜张力假定,则纵桥向单位长度膜刚度(EA)索/d与拱肋抗弯刚度应存在一定的相关性。图6为单位长度膜刚度与拱肋抗弯刚度分布图。由于吊杆设计安全系数一般取2.5~3,但没有安全系数的上限值的规定,使得吊杆实际安全系数的取用会因人而异,统计规律离散性也较大,但基本表现为吊杆轴向刚度随拱肋抗弯刚度的增大而增大。将其按线性关系拟合如下:
(7)
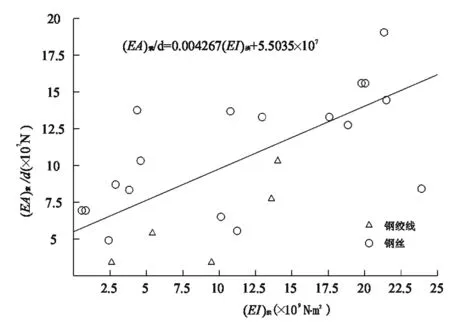
图6 吊杆膜刚度与拱肋抗弯刚度拟合曲线图
3 分析模型设计
为讨论方便,不考虑桥梁横向布置对结构受力影响。在确定跨径、设计荷载后,由式(4)~(7)即可设计出一组不同拱梁刚度比的下承式简支梁拱组合桥:计算跨径80m,矢跨比为1/5,吊杆间距5m,单片拱肋承担活载为:单车道公路II级(不考虑冲击力)。不同拱梁刚度比模型的构件设计参数如表1,模型纵断面示意如图1。
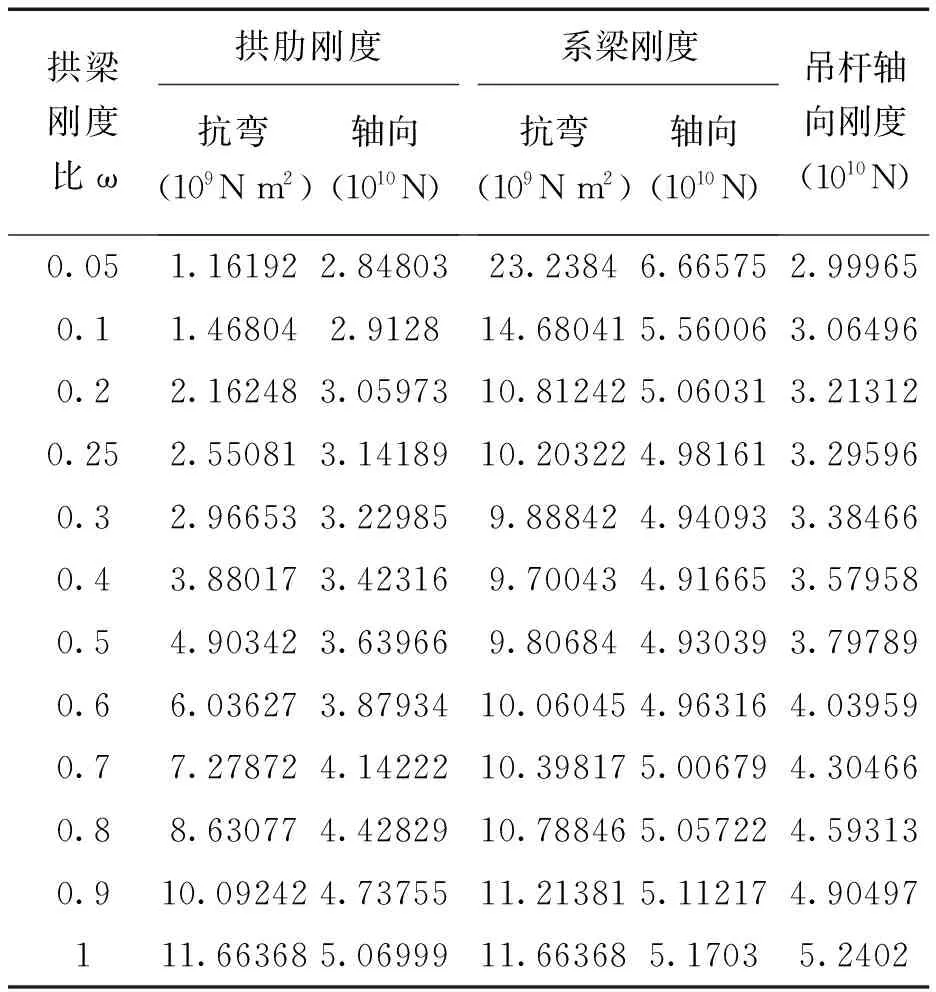
表1 下承式简支梁拱组合桥主要构件设计参数表
通过对该组模型进行数值分析,得出常见下承式简支梁拱组合桥在活载作用下的受力规律,以确定其控制截面及静载试验工况。
4 静载试验工况分析
桥梁静载试验主要测试结构承载能力指标(应变、挠度等),而结构的最不利受力部位必须是结构承载力的关键,也应是测试控制部位[11]。因此通常根据桥梁结构的内力、挠度包络图,并考虑应力分布,按最不利受力原则选定截面,然后拟定试验工况[2]。
根据表1中设计参数,利用midas/civil分别建立模型,计算汽车荷载作用下拱肋、系梁的内力(弯矩、轴力)及挠度,以确定静载试验控制截面及工况。
4.1 弯矩工况分析
各模型在汽车荷载作用下拱肋、系梁的弯矩包络图变化趋势相似。图7、图8分别示出了ω=0.5时,拱肋、系梁在汽车荷载作用下的弯矩包络图(半桥)。拱肋系梁弯矩均以底缘纤维受拉为正,这与一般规定以拱肋-系杆体系的闭合图形外侧受拉为正略有区别。图示表明:
弯矩最大值出现在1/4跨附近而非跨中。因此弯矩工况的控制断面应选在四分点附近。
同时受吊杆位置的影响拱肋或系梁的弯矩图呈现折线变化;拱肋最大正弯矩、系梁的最大负弯矩一般出现在吊杆处;拱肋最大负弯矩、系梁的最大正弯矩一般出现在两吊杆之间。表明最大正、负弯矩控制截面并不在同一截面。
L/4截面附近拱肋、系梁均是正弯矩较大,一般应做正弯矩工况;但拱肋最大负弯矩达到正弯矩的77%,而系梁最大负弯矩也达到正弯矩的55%左右。因此可同时考虑最大负弯矩工况。
与一般拱桥不同,下承式简支梁拱组合桥在拱脚附近并未出现较大的弯矩,可不必设置拱脚最大弯矩工况。

图7 拱肋最大最小弯矩包络图(半桥)
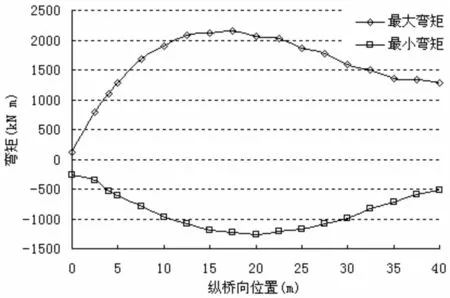
图8 系梁最大最小弯矩包络图(半桥)
图9、图10分别示出了拱肋与系梁主要截面弯矩变化曲线图。其中拱肋(或系梁)最大/最小表示拱肋(或系梁)的最大正弯矩/最小正弯矩。图示表明:
拱肋1/4跨处最大正弯矩与拱肋最大相差不超过1%,而最大负弯矩在ω>0.3时,也不超过5%。系梁1/4跨处最大正弯矩与系梁最大相差不超过6%,而最大负弯矩则出现在1/4跨处。可见拱肋、系梁弯矩最大最小值虽不出现在同一截面内,但相差并不大,因此静载试验中最大最小弯矩控制截面可取同一截面。
当ω≤0.1时,拱肋控制弯矩虽不到系梁弯矩的10%,但考虑到该情况下,拱肋截面刚度较小,其应力水平较大,因此建议仍进行相应的弯矩工况。
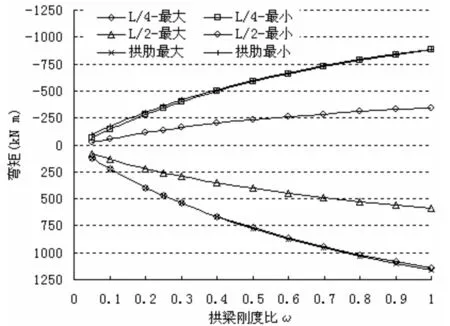
图9 拱肋主要截面弯矩随拱梁刚度比变化图
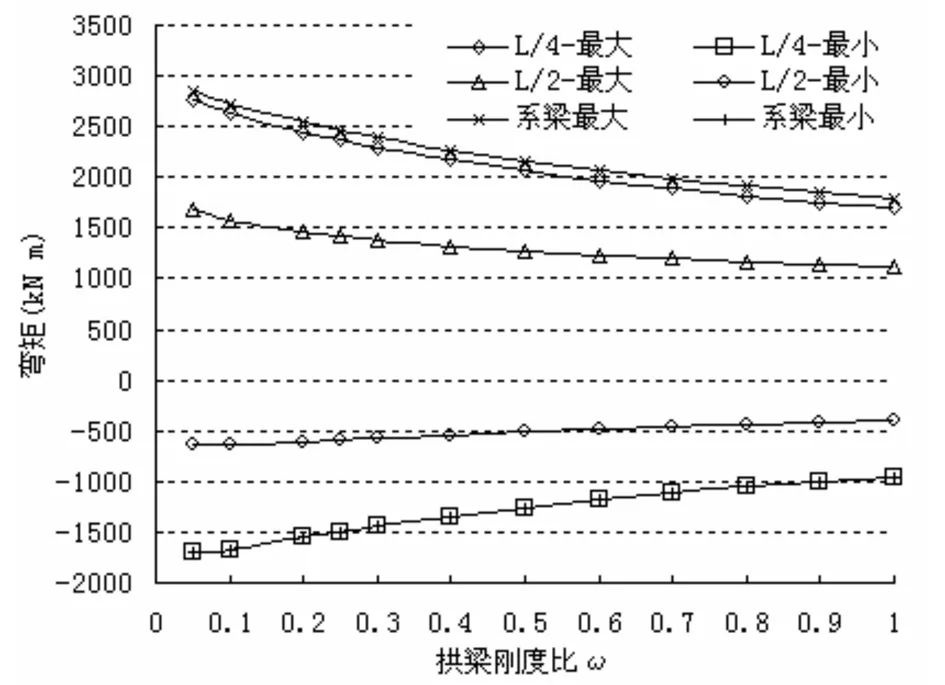
图10 系梁主要截面弯矩随拱梁刚度比变化图
4.2 轴力工况分析
各模型在汽车荷载作用下拱肋、系梁的轴力变化趋势相似。图11、图12示出了ω=0.5时,拱肋轴向压力、系梁轴向拉力的分布图(半桥)。图示表明:
拱肋轴压力分布变化较均匀,由拱顶向拱脚逐渐增大,因此拱肋最大轴力况的控制截面为拱脚。
系梁除梁端截面因构造加强,使轴力略有变化,其它截面轴力几乎不变。结合式(1)可见轴力对抗弯刚度贡献主要由矢高决定,也是最大正弯矩并未出现在跨中的原因。结合弯矩控制截面的选取,可将系梁最大轴力控制截面选择在L/4截面处或跨中。
图13、图14则为拱肋、系梁主要截面轴力随拱梁刚度比变化曲线图。

图11 拱肋最大轴压力包络图(半桥)
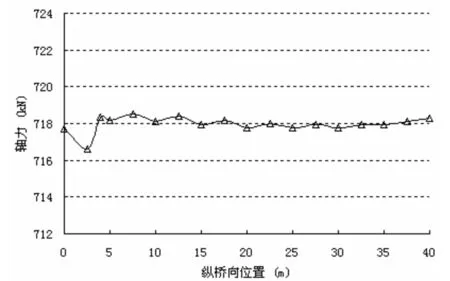
图12 系梁最大轴压力包络图(半桥)

图13 拱肋主要截面轴压力随拱梁刚度比变化图
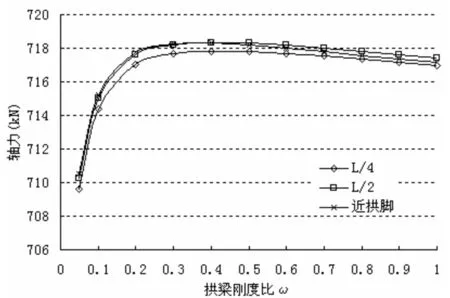
图14 系梁主要截面轴拉力随拱梁刚度比变化图
由图可见,拱肋、系梁主要截面轴力随拱梁刚度比变化均不超过3%,表明拱、梁水平力抵抗弯矩在各模型中几乎是不变的。因此从应力角度考虑,若拱梁刚度比较小且拱肋刚度也较小时,须考虑拱肋压力工况。反之拱梁刚度比较大且系梁刚度较小时,可能须要考虑系梁的拉力工况,本文中各模型系梁刚度均较大,可不考虑。
4.3 挠度工况分析
各模型在汽车荷载作用下拱肋、系梁的挠度变化趋势相似。图15、图16分别示出了ω=0.5时,拱肋、系梁的挠度包络图(半桥),图中挠度以向上为正。
拱肋、系梁最大正负挠度均出现在1/4跨位置,而跨中挠度则明显较小。同时挠度为宏观量,受局部受力或构造影响较小,挠度曲线较平滑。表明挠度工况的设置或挠度测点的布置,几乎不受吊杆位置的影响。
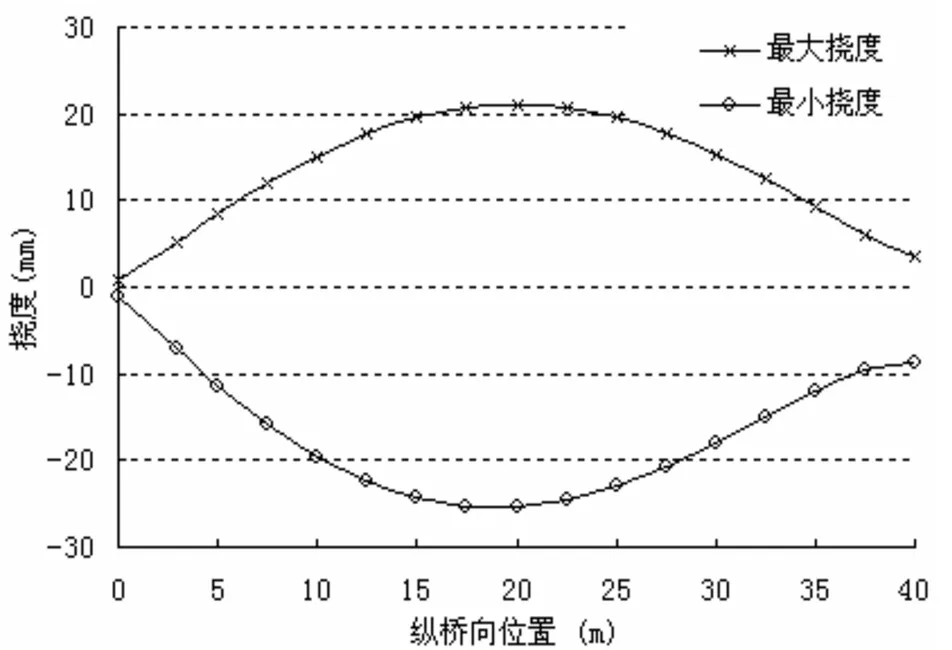
图15 拱肋最大最小挠度包络图(半桥)

图16 系梁最大最小挠度包络图(半桥)
图17、图18分别为拱肋、系梁挠度随拱梁刚度比变化曲线,图示表明:
各种拱梁刚度比下,拱肋L/4截面最大正挠度约为最大负挠度的80%左右,而系梁L/4截面最大正挠度约为最大负挠度的70%左右,因此宜考虑最大正、负挠度绝对值之和工况。
图中显示ω=0.25时,结构挠度最大,主要是因为模型中系梁刚度随拱梁刚度比的增加是先减小后增大的。

图17 拱肋挠度随拱梁刚度比变化曲线图
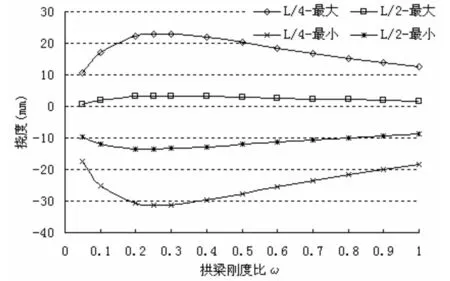
图18 系梁挠度随拱梁刚度比变化曲线图
5 结 语
通过对不同拱梁刚度比的桥梁主要构件的内力、挠度分析,对常见下承式简支梁拱组合桥(0.05≤ω≤1.0),推荐荷载试验主要工况如下:
(1)拱肋L/4截面附近最大正弯矩,最大负弯矩;
(2)拱肋L/4截面附近最大正、负挠度绝对值之和;
(3)系梁L/4截面附近最大正弯矩,最大负弯矩。
推荐附加工况如下:
(1)当拱梁刚度比较小,且拱肋刚度较小时,拱脚最大轴向压力;
(2)当拱梁刚度比较大,且系梁刚度较小时,系梁跨中或四分点最大轴向拉力。
[1]顾安邦,向中富.桥梁工程(下册)[M].北京:人民交通出版社,2011.
[2]JTG/T J21-2011,公路桥梁承载能力检测评定规程[S].
[3]JTG/T J21-01-2015,公路桥梁荷载试验规程[S].
[4]李万恒,沈红军.西塘大桥主桥静、动荷载试验[J].公路交通科技,2004,21(9):60-63.
[5]高晓燕,张浩,张晓炜,等.蒲山特大桥静动载试验及质量评定[J].中外公路,2010,30(4):360-364.
[6]金成棣.预应力混凝土梁拱组合桥梁-设计研究与实践[M].北京:人民交通出版社,2001.
[7] 肖汝成,等.桥梁结构体系[M].北京:人民交通出版社,2013.
[8]陈程.系杆拱桥受力特性及其类型划分析[D].沈阳:东北大学,2011.
[9]杨俊杰.相似理论与结构模型试验[M].武汉:武汉理工大学出版社,2005.
[10]易云,肖汝诚.下承式梁拱组合桥梁的梁拱协作机理研究[J].力学季刊,2007,28(1):153-159.
[11]谌润水,胡钊芳.公路桥梁荷载试验[M].北京:人民交通出版社,2003.
Static Load Test Study for Through Beam-arch Combination Bridge with Simply Supported
SHI Jie1, WANG Rong-bo2
(1. Zhejiang Zhe-jiao Detection Co.,Ltd, Hangzhou 310015,China;2 North China Municipal Engineering Design & Research Institute Co. Ltd., Chengdu Branch,Chengdu 610031,China)
The mechanical properties of through beam-arch combination bridge with simply supported is analyzed, to determine the main influence parameters for structural resistance. The design parameters of 26 beam-arch combination bridges with simply supported were processed. In order to gain the rule between flexural rigidity of arch rib and the stiffness ratio of arch rib to beam, between arch rib or beam section flexural rigidity and their axial stiffness, between axial stiffness of the suspender and flexural rigidity of arch rib. Finally the correlation equations of various parameters were gained. A set of bridge model which are in the same span calculation, design load, but different stiffness ratio of arch rib to beam were designed. Using finite element analysis program, the rule of the bending moment, axial force and the deflection were analyzed, and the most unfavorable loading sections were determined. On the basis of above, the recommended static load test conditions of the bridge are presented.
bridge engineering; beam-arch combination bridge; finite element analysis; static load test;test condition
2016-11-02
史 杰(1984-),男,安徽宿州人,工程师,硕士,E-mail:shijie1234567890@163.com。
U446.1
A
10.3969/j.issn.1671-234X.2016.04.002
1671-234X(2016)04-0006-07

