基于多重服务时限的物流中心选址双层规划模型研究
唐佑绵, 刘 涛, 刘书君
(1. 新疆农业大学 机械交通学院,乌鲁木齐 830052;2.新疆交通科学研究院 干旱荒漠区公路工程技术交通行业重点实验室,乌鲁木齐 830000)
基于多重服务时限的物流中心选址双层规划模型研究
唐佑绵1, 刘 涛2, 刘书君2
(1. 新疆农业大学 机械交通学院,乌鲁木齐 830052;2.新疆交通科学研究院 干旱荒漠区公路工程技术交通行业重点实验室,乌鲁木齐 830000)
目前物流配送活动大多是以服务时限为原则安排配送的时间与路径,根据此原则提出了基于多重服务时限的物流中心选址双层规划模型。该模型一方面考虑了物流服务提供方的基础建设投资、配送成本、环境污染成本、时间成本和其它临时变动成本,另一方面也考虑了客户对不同服务时限的要求。最后,运用聚类分析和启发式算法对模型进行求解,并通过模拟算例对模型的有效性进行验证。
服务时限;物流中心;双层规划;启发式算法
0 引 言
在物流中心理论定义中,其核心是实现运输工具的最佳互连,以产生最佳的交通流和形成每个区域最适合的网络物流中心。此外,物流中心是满足不同运输方式的枢纽,为铁路、公路和航空等交通运输链的组合提供了最佳的条件[1]。
事实上,城市物流已成为一个城市的增长和发展的重要组成部分。先进的城市物流系统可以提高经济增长率,减少不必要的交易成本,改善投资环境,解决城市失业和促进区域经济的发展。然而,研究也表明,城市物流体系的最后一公里是最贵的,是整个供应链的最低效部分。因此,有必要改善城市物流,使人们能在高质量的环境中生活和工作[2]。物流中心作为整个物流系统中关键环节显得尤其重要,而选址的合理性直接关系到企业和客户的成本,同时也将对城市交通、区域发展、环境、居民生活质量等各方面产生较大的影响。
在物流中心选址与设计中,一般做法是通过建立数学模型和量化影响因素进行分析求解。根据影响因素的性质可将选址方法分为定性和定量两大类。定性的方法主要是针对影响因素无法量化的选址问题,代表性方法的有层次分析法和专家选择法。定量的方法是将影响因素量化代入到选址模型中,求解模型找到最合适的备选点,代表性的方法有重心法、Blson模型、Kuehn-Hamburrger模型以及Baumol-wolfe模型等。另外,有学者还给出了九个基本的选址模型[3]。这些针对物流中心选址问题所提出方案理论的主要思想是在一系列候选点中确定新增设施的最佳位置,目标是使各项费用最小。
近年来,国内学者还提出了一些新的物流中心选址方法。张席洲、龚奇才等提出了基于GIS的物流中心选址方法[4];李琳、张振飞、刘泊等提出了基本博弈论思想的区域物流中心选址方法[5];谭凌、高峻峻、王迎军等对基于库存成本优化的物流中心选址问题进行研究[6];李卫江、郭晓汾、张毅、龚延成等提出了基于Matlab优化算法的物流中心选址[7];陆琳琳、张仁颐等给出了新的全面考虑上、下游物流活动的物流中心选址模型[8];杨波研究了多品种随机数学模型的物流中心选址模型[9];张培林、魏巧云等提出了有关多个物流中心的选址模型[10];王淑珍和振兴等提出了在不确定需求情况下,运用非线性规划方法构建及实现了基于鲁棒性优化的城市物流中心选址模型[11]。
在实际应用中学者们发现单独使用一种理论或方法进行选址的效果并不十分理想,而用两种或多种方法综合运用的复合型选址方法得到的备选点契合度更高。常见的复合型选址方法有基于重心法与层次分析法相结合的物流中心选址方法[12]、基于AHP/DEA的物流中心选址方法[13]以及连续与离散相结合的单一物流中心选址方法等[14]。
本文以在多重时限条件下物流终端点送达覆盖率和货物总量送达覆盖率的概念为基础,提出了基于多服务时限的物流中心选址双层规划模型。该选址模型在考虑物流中心建设成本、配送费用、时间成本、污染环境成本和物流中心本身维持基本运营的成本和其它临时变动成本等的同时也考虑了客户对服务时限的要求。然后,模型以聚类与用户级别优先为原则进行路径规划,并通过上下层函数反馈机制及启发式算法进行迭代求解,最后,通过一个简单模拟算例对模型的有效性进行了验证。
1 基于多重服务时限的物流中心选址双层规划模型
在客户对企业的物流服务水平反馈中,货物送达的时间是客户最关心的问题。对于生产企业或物流公司而言,物流终端多、分散广和类型杂是他们必须面对的问题,而要以最短时间到达所有物流终端点是不切实际的。目前,物流配送活动中是根据配送货物量、客户支付的费用、货物性质等因素对客户进行分级,以级别高低安排配送时间,其中,服务时限是衡量客户级别的显著性指标。对于客户而言,当区域中某一物流中心服务时限较其他物流中心有明显优势时,将对客户产生较强的吸引力,从而导致该物流中心客户大量增加,相应的将降低物流配送能力与服务水平(通常来说是服务时限的延长)。因此,客户与物流中心之间是一个相互影响-调整策略-再影响-再调整策略循环往复的过程。从很大程度上讲,配送时限反映的是物流中心在考虑客户级别下配送路径最优化的问题。一般来说,客户级别越高,服务时限越短。多重服务时限下的物流中心选址双层规划模型是基于这一原理,最终目标是要实现广义上物流费用最低。
1.1 物流终端点送达覆盖率和货物总量送达覆盖率定义
物流终端点送达覆盖率是指定的服务时限内,货物送达到终端网点个数与物流服务提供商可以服务的全部物流终端网点的比值。货物总量送达覆盖率是指所指定的服务时限内,物流服务提供商对物流终端点送达量与总配送量的比值。
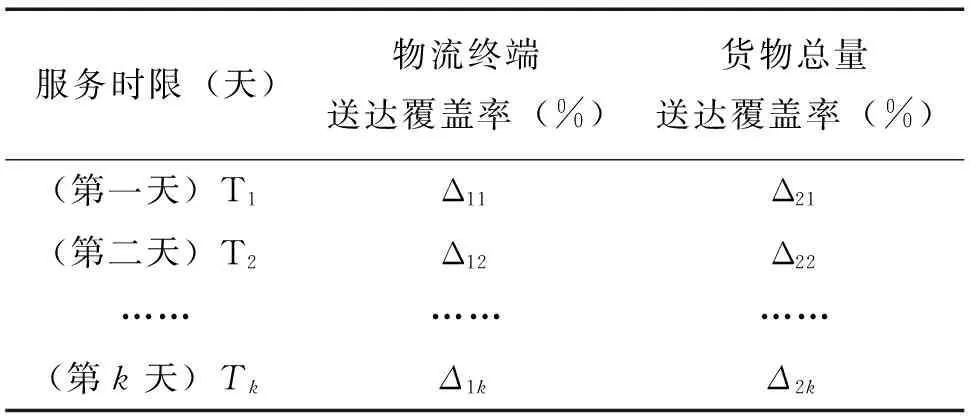
表1 物流终端点送达覆盖率和
显然,Δ11,Δ12,…,Δ1k和Δ21,Δ22,…,Δ2k单调增加,且有Δ1k=1,Δ2k=1,(当k→∞时),在实际操作中根据具体要求设置。设有m个需求点(用i来表示),n个物流中心选址候选点(用j表示),设选择的运输工具的平均行驶速度是v。用k个0-1函数a1ij,a2ij,…,akij来判断物流中心j对需求点i 的服务时限。设置式(1)所示:
(1)
1.2 基于多重服务时限的物流中心选址双层规划目标函数
模型假定:(1)在待建物流中心所在区域不存在其它已有的物流中心;(2)道路交通处于畅通的状态,即实时交通不会对配送路径和配送时间产生影响;(3)客户与物流中心之间距离以及客户与客户之间的距离取两点间的直线距离;(4)模型中任一备选物流中心都能满足所有客户的需求。
上层目标函数,见式(2)为广义费用函数,反映的是基础设施投资、配送费用、时间成本、污染环境成本和物流中心本身维持基本运营的成本和其它临时变动成本。
s.t.


zj∈{0,1}
(2)
式中: dij为第i个需求点到第j个物流中心的配送里程;pij为第i个需求点到第j个物流中心的平均运费;tij为第i个需求点到第j个物流中心的车辆行驶时间;y(vij)为第i个需求点到第j个物流中心平均车速下的污染物排放函数;a为处理污染物的单位成本;Ca为其它临时变动成本,一般情况下为零;gij为物流中心处理第i个需求点到第j个物流中心配送量的单位运营成本(包括人员费、水电费和设备运营费等);Xij为第i个需求点在j物流中心得到的需求量; B为修建物流中心的总投资预算; fj为在j地建物流中心的基础设施投资;zj表示在j地建物流中心时,此值为1,否则为0;θ为匹配总费用与需求点需求量的系数;F为总费用。
下层目标函数,见式(3)为在多个候选物流中心条件下的客户配送方案函数,反映多重服务时限条件下不同的物流配送方案的总费用,目标是使配送方案按客户级别进行最优规划,从而使广义的物流费用降至最低,并将最优化的配送路径反馈给上层目标函数。
(3)
s.t.

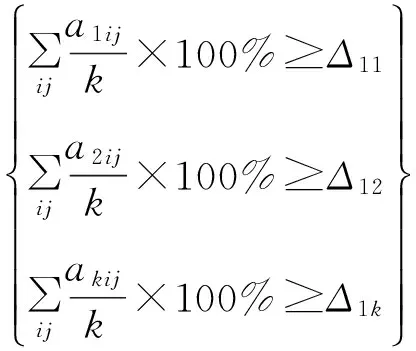
⑤
⑥
式中:约束条件①表示任意第i个物流终端点对物流服务的需求能完全满足;约束条件②表示新建物流中心的最大配送量始终大于或等于物流终端点的需求量;约束条件③表示物流终端点的需求量只在已有的物流中心进行配送;约束条件④保证变量始终为正数;约束条件⑤表示物流中心对物流终端点送达覆盖率的要求;约束条件⑥表示物流中心对货物总量送达覆盖率的要求。其中D-1(·)为W(总需求量函数)的反函数;Wi为物流终端点i的总需求量;Sj为j地物流中心所能提供物流能力;M为任意大正数;△11,△12,…,△1k为物流终端点送达覆盖率,△21,△22,…,△2k为货物总量送达覆盖率;qi为第i个需求点处的需配送的货物数量;Q为总配送量;T为对应总配送量的总费用。
2 模型求解
传统的配送路径假设从物流中心出发,经过巡回路径访问各个客户后返回,而在考虑客户级别时须优先给高级别客户进行配送,因此,相应的配送方案和路径与传统的配送方式大不相同,而在现实物流活动中,配送路径要复杂得多。根据聚类方法,考虑不同服务时限和客户与物流中心距离,按同一条配送路径和同一个物流中心提供服务原则进行分类,然后对每一类估计费用值,并根据配送路径的长度和车载上限得出一次配送活动的单位运输成本Cij,见式(4)。
(4)
其中:dj、pj、tj、y(vj)、gj分别为从j个物流中心出发的配送里程、平均运费、配送时间、污染物排放函数和物流中心的单位运营成本。
2.1 基于启发式算法的求解过程

(3)重复以上过程,进行迭代运算,当精度值e满足设计要求时,停止运算。其中e值可用迭代后项所得的总成本F值减去前项总成本F值的绝对值得到。
3 模拟算例
(1)假定条件: 3个客户(C1,C2,C3),2个物流中心备选点(P1,P2)。其中C1为最高级别客户(A级,当日送达),用☆表示,C3为较高级别客户,用▲表示(B级,次日送达),C2为普通客户(C级,第三日送达),用△表示,◎代表物流中心备选点;需求点、需求量分别为Q1=100 ,Q2=70,Q3=40;总需求量函数所对应的反函数为D-1(xij)=μj(Xij)φj-vjZj,其中μj、φj为匹配不同物流中心配送量的参数,Vj为从j个物流中心出发的平均行驶速度。可假设μ1=0.3,μ2=0.4,φ1=0.5,φ2=0.5,V1=6,V2=2,V3=10,f1=20,f2=16,B=40,θ=200,M=200。需求点之间的距离dC1C2=30,dC2C3=50,dC1C3=40。同时,设运输工具的载货量为200,两个物流中心可完全满足需求点的要求。另外,设第一天(T1)达到物流终端点送达覆盖率为30%和货物总量送达覆盖率为40%,第二天(T2)达到物流终端点送达覆盖率为60%和货物总量送达覆盖率为60%,第三天(T3)达到物流终端点送达覆盖率为90%和货物总量送达覆盖率为90%。

图1 模拟配送方案
(2)计算如下:
①设物流中心备选点P1、P2已经投入使用,令Z0=(1,1);
②对于给定的Z0=(1,1)代入到下层函数中,按物流中心点P1、P2到C1、C2、C3的2范数和级别优先原则排序,形成配送路径,从P1出发的配送路径为P1→C1→C3→C2→P1,从P2出发的配送路径为P2→C1→C3→P2→C2→P2,模拟配送方案如图1所示。
③在限制条件1_6下求解下层目标函数,3个需求点的需求量在第一个物流中心份额为:(63,0,43.48),3个需求点的需求量在第二个物流中心的份额为:(37.8, 40,25.72)
线性关系为:X11=200z1-137.88;X21=200z3-200;X31=200z3-156.52;X12=200z2-162.2;X22=200z3-160;X32=200z3-173.48。此时由P1点出发的模拟配送方案终端点送达覆盖率△11=33.3%>30% ,△12=66.7%>60%,△13=100%>90%;货物总量送达覆盖率△21=47.6%>40% ,△22=66.7%>60%,△23=100%>90%。由P2点出发的模拟配送方案终端点送达覆盖率△11=31.9%>30% ,△12=64.3%>60%,△13=93.5%>90%;货物总量送达覆盖率△21=45.1%>40% ,△22=61.7%>60%,△23=96.8%>90%,均符合要求。
④根据3个需求点与物流中心之间的距离dC1P1、dC2P1、dC3P2、dP2C2、dC2C3和dC1C3的,计算每条配送线路上的广义运输成本Cij。为简化运算,可令上层函数括号内的数值为物流中心完成一个配送任务的广义单位费用用Cij表示,即Cij=[dijpij+tij+ay(vij)+gij],在此算例中可令C11=0.3,C21=0.4,C31=0.5,C12=0.5,C22=0.3,C32=1.0。(Cij值在实际操作中要根据具体的dij、pij、tij、a、y(vij)和gij值进行测算)
⑤将Xij和Cij代到上层目标函数中,利用branch-and-bound方法求解上层目标函数,得出一组备选方案(z1=1,z2=0),说明在P1处更适合新建物流中心。
5 结 语
基于多重服务时限物流中心选址双层规划模型在考虑物流服务提供商总成本的前提下,创新性地引入了服务时限因素,与现行的物流配送方式较为吻合,因此具备较强的实用性。通过模型求解及案例分析可以验证该模型的有效性。但由模型假设可知,该模型目前仅适用于无物流中心区域新建物流中心的情境,并且模型未考虑交通阻抗的影响。当道路交通处于饱和或超饱和状态时,对送达时间或配送路径肯定会产生明显影响,因此,模型还有待进一步深入研究。
[1] Kampf R,Kolá? J,Lejsková P.Assessment Plan for Location of Distribution Centres[J].Applied Mechanics & Materials,2014,(708):324-329.
[2] Rao C,Goh M,Zhao Y,et al.Location selection of city logistics centers under sustainability[J].Transportation Research Part D Transport & Environment,2015, (36):29-44.
[3] Aikens C H.Facility location models for distribution planning[J].European Journal of Operational Research,1985,22(3):263-279.
[4] 张席洲,龚奇才.基于GIS的物流中心选址[J].物流技术,2005,(10):249-252.
[5] 李琳,张振飞,刘泊.基于博弈论思想的区域物流中心选址方法[J].物流科技,2006, 29(1):122-124.
[6] 谭凌,高峻峻,王迎军.基于库存成本优化的配送中心选址问题研究[J].系统工程学报, 2004,19(1):59-65.
[7] 李卫江,郭晓汾,张毅,等.基于Matlab优化算法的物流中心选址[J].长安大学学报:自然科学版,2006,26(3):76-79.
[8] 陆琳琳,张仁颐.一种新的物流中心选址方法[J].物流科技,2003,26(3):28-30.
[9] 杨波.多品种随机数学模型的物流配送中心选址问题[J].中国管理科学,2003, 11(2):45-49.
[10] 张培林,魏巧云.物流配送中心选址模型及其启发式算法[J].交通运输工程学报,2003, 3(2):65-68.
[11] 王淑珍,和振兴.不确定需求情景下的一种城市物流中心选址方法[J].铁道科学与工程学报,2011,8(4):106-110.[12] 孙焰,李云峰.物流中心选址的两阶段法研究[J].物流科技,2006,29(5):41-44.
[13] 张敏,杨超,杨珺.基于AHP/DEA的物流中心选址问题研究[J].管理学报,2005, 2(6):641-644.
[14] 孟祥海,苗鑫.连续与离散相结合的单一物流中心选址方法[J].哈尔滨工业大学学报,2006,38(7):1055-1058.
Research on Bi-level Programming Model of Logistics Center Location Based on Multiple Service Time Limits
TANG You-mian1, LIU Tao2, LIU Shu-jun2
(1. School of Mechanical and Transportation, Xinjiang Agricultural University, Urumqi 830052, China ; 2. Key Laboratory of Highway Engineering Technology in Arid & Desert Region, Ministry of Transport, Xinjiang Academy of Transportation Science, Urumqi 830000, China)
Most of the logistics distribution activities are based on the service time limit to arrange time and route of delivery in current situation, according to this principle paper presents the bi-level programming model of logistics center location based on multiple service time limits. On the one hand, the model considers the basic construction investment, distribution costs, environmental pollution cost, time cost and other temporary variable costs of logistics service providers, on the other hand, it also considers the requirements of different service time limits of customer. Finally, the model is solved by clustering analysis and heuristic algorithm, and the validity of the model is verified by simulation case.
service time limit;logistics center;bi-level programming;heuristic algorithm
2016-09-24
唐佑绵(1983-),男,湖南株洲人,硕士,E-mail:28639775@qq.com。
U492.3
A
10.3969/j.issn.1671-234X.2016.04.009
1671-234X(2016)04-0044-05

