基于多目标优化设计的多轴永磁同步电动机控制系统研究

郑 彬，王茂森，戴劲松

(南京理工大学，南京 210094)

基于多目标优化设计的多轴永磁同步电动机控制系统研究

郑 彬，王茂森，戴劲松

(南京理工大学，南京 210094)

为了更好地满足各类永磁同步电动机在不同工况下对电机性能目标的多样化需求,介绍了一种在MATLAB中进行多目标最优控制算法设计方法。采用JMAG进行实际PMSM物理模型仿真，得到更为直接真实的观测结果并依据结果分析得出最优方案。利用FPGA完成单芯片资源定制式高性能多轴永磁同步电动机控制系统设计。其后，本文依据该高性能永磁同步电动机控制系统设计方法，通过能源利用最优、转矩特性最好的多目标多永磁同步控制典型实验，证明其效果优越。该项研究可为定制化制造及高性能专用电机控制提供一定的借鉴意义。

多轴;永磁同步电动机；FPGA；多目标最优；定制式；MATLAB；JMAG

0 引 言

永磁同步电动机具有体积小、质量轻、效率高、控制性能高等优势[1]，近几年在工业生产、电动汽车、机器人等领域得到了广泛的应用[2]。但由于其在工作过程中具有多场强耦合的特点，理论分析上具有很高的难度，这成为高性能永磁同步电动机控制策略针对性设计的难点[3]。为此，本文利用JMAG进行更为真实的PMSM运行仿真。

现今市面上许多MCU或DSP控制板具有通用的控制电路及相应的驱动模块[4]，但是，这些控制板的高速存储空间有限，模拟信号采集范围较窄、PWM通道数量有限，无法满足高性能多轴永磁同步电动机控制系统的需求。下一代驱动器将会对驱动性能提出更高的需求，如效率、稳定性、寿命、实时性、多轴并行控制等，而采用FPGA作为驱动器可以实现上述多项功能，因此FPGA可以成为下一代主流驱动器。

目前，基于FPGA的多永磁同步控制器设计研究的学者主要集中在高校和研究所[5]。从国内外文献上可以看到，进行此类研究并取得一定成果的还不多，而针对PMSM多目标控制系统设计的研究则更加少。随着我国工业4.0战略的到来，基于多目标优化设计的多轴永磁同步电动机控制器设计，将在节约能源、提高性能等方面发挥重要作用。

为了更好地在实现单电机多目标优化最优控制的同时，进行PMSM并行控制，本文在MATLAB中建立针对多目标的控制方法设计，使用JMAG进行PMSM运行仿真，并将MATLAB设计的电机控制方法与其对接。通过对指定控制方法下电机的热场分布、磁滞情况、能量消耗、退磁等进行分析，可以得到增强型磁场定向控制(FOC)策略控制系统的最优控制参数，从而实现多目标定制式最优控制方法的设计。并将MATLAB控制方法模型转入Quartus II中，建立各PMSM目标针对性的片内检测与控制电路。通过参数及模块的调整、组合，实现单芯片多目标定制式多电机控制系统的设计。

1 多目标优化设计的PMSM控制系统设计流程

在工业能耗领域中，来自工业电机驱动设备的能源消耗量占了总能耗的2/3以上[6]。因此，为了更好地降低工厂生产费用，提高生产质量，高效的电气控制性能成为了核心要素[7]。

1) 在工业自动化设备电机控制设计中，企业在使用电机的时候通常会以电机转矩控制特性、速度控制特性、电机振动情况、电机温度控制、电机寿命提出不同的目标需求[8]。

2) 往往在同一个设备的不同部位，电机的控制性能需求可能完全不同。如在机床中，控制主轴和风扇的驱动器有不同的要求和反馈机制。

3) 由于不同厂商生产的同一类型电机在结构和材料上也都存在一定的差异。为了更好地利用电机的性能，节约成本，设计针对所使用电机的专用针对性控制策略，以进一步提高电机的控制性能。

采用本文介绍的基于多目标优化设计的多轴永磁同步电动机控制方法，具有设计周期短、综合性能提高显著、设计成本低、面积小、稳定性高等诸多优点。

1.1 JMAG仿真设计

为解决电机多场强耦合(如图1所示)、非线性时变系统理论分析的瓶颈和在实际环境下部分特性无法测量的困难，更好地了解电机内部工作情况。使用JMAG进行电机参数化快速建模，并通过仿真了解电机各场情况及工作性能特性曲线，如：热场分析、铁损分析、转矩分析、退磁分析等。

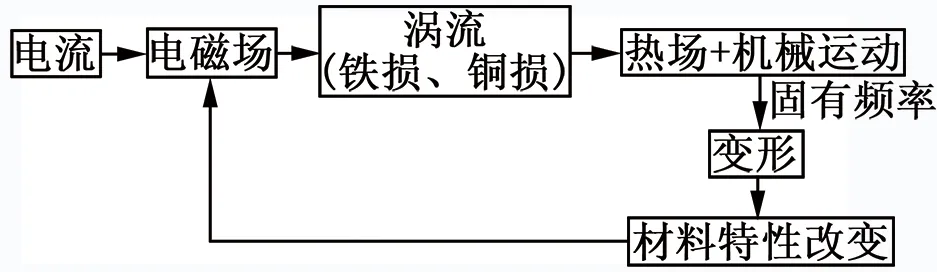
图1 双向耦合系统框图

1.2 MATLAB控制算法设计及仿真

为提高电机控制性能的鲁棒性及各项控制性能，针对应用模型建立对应的数学模型。通过JMAG-RT将电机模型导入Simulink当中，形成控制单元。由于多电机运动控制在数控机床及机器人领域广泛应用，本文在MATLAB中建立如图2机械手臂增强型FOC控制策略控制系统模型。采用数学模型与反馈机制并行控制的方式，通过基于模型的重力距及关节间力矩的评估(Ta，Td)，减少控制的波动，实现快速响应。采用物理场与控制模型双向对接的方式，可以实时地了解各场及控制特性情况，从而寻找定制目标最优控制参数解。

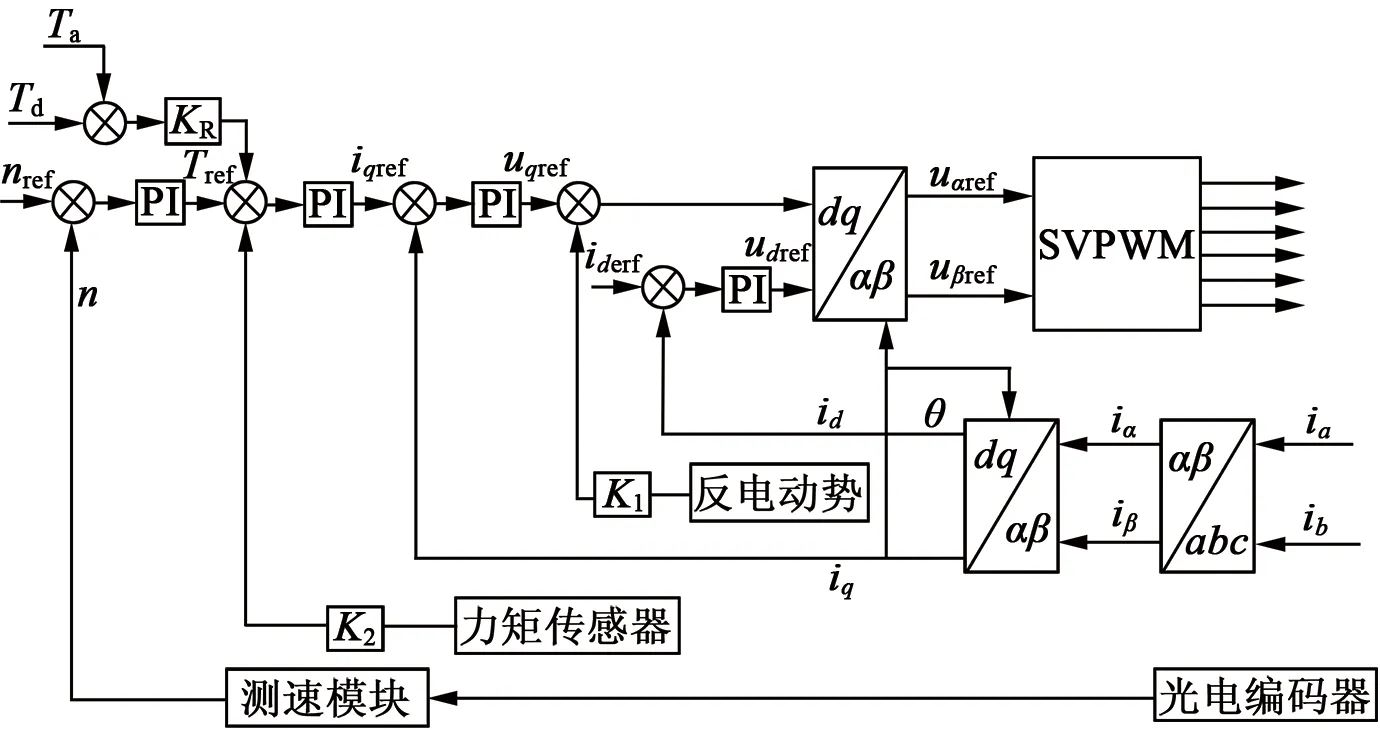
图2 机械手臂增强型FOC控制方法

通过MATLAB/Simulink求得最优仿真控制策略模型，后将其控制策略模型利用DSP Builder导入FPGA当中形成专用IP核。

在增强型FOC控制策略中的关节间力矩估计中，我们将机器关节看作刚体结构。其电动机-齿轮-负载联合装置传动结构如图3所示。

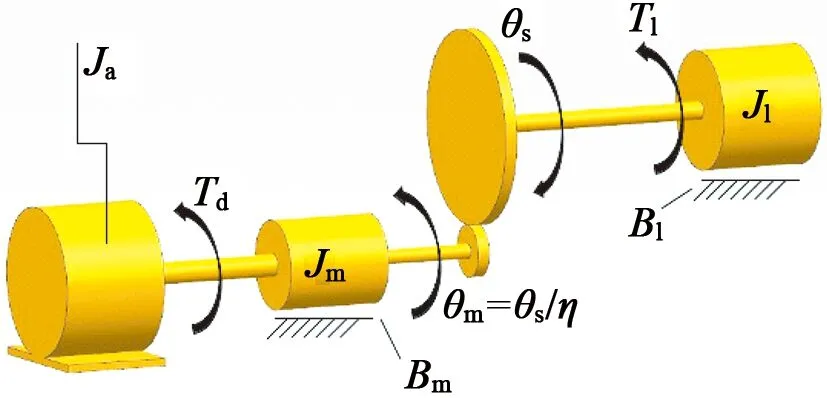
图3 机器关节传动示意图

图3中，Ja为驱动电机侧转动惯量；Jm为传动侧等效转动惯量；Jl为连接杆侧转动惯量；Bm为传动侧阻尼系数；Bl为负载侧阻尼系数；θm为传动侧角位移；θs为负载侧角位移；η=rm/rs=Nm/Ns为减速齿轮的传动比。

令F为从电动机传至负载的作用在齿轮啮合点上的力，则

Tl′=Frm

(1)

Tl′为电动机轴侧的等效负载力矩，而且

Tl=Frs

(2)

又因为θm=2π/Nm,θs=2π/Ns,所以

θs=θmNm/Ns=ηθm

(3)

传动侧、负载侧角速度和角加速度关系如下：

(4)

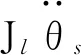
(5)

或写为：

(6)

在传动轴一侧，同理可得：

(7)

得到下式：

(8)

整合得到关节间力矩：

(9)

在增强型FOC控制策略矢量控制中，采用三相静止的ABC坐标系、两相静止的α-β坐标系和两相旋转的d-q坐标系。通过旋转坐标变换，对电机的数学模型进行解耦。

根据以上理论，可以推导出ABC静止坐标系到α-β静止坐标系的坐标变换矩阵，又称为Clarke变换矩阵：

(10)

从α-β两相静止坐标系转换为ABC三相静止坐标系的坐标变换称为Clarke逆变换。其变换矩阵：

(11)

从两相静止的α-β坐标系转换为两相旋转的d-q坐标系的坐标系变换被称为Park变换。其变换矩阵：

(12)

从d-q两相旋转坐标系转换为α-β两相静止坐标系的坐标变换为Park逆变换。其变换矩阵为：

(13)

其电压方程：

(14)

其磁链方程：

(15)

其电磁转矩方程：

(16)

1.3 FPGA控制算法实现

为更好地降低多PMSM控制器的开发成本，提高多PMSM控制器的控制性能，该驱动器充分利用FPGA柔性化设计的特点，通过使用FPGA片内处理器及灵活的DSP资源，实现精度可调的浮点型磁场定向控制或直接转矩控制(DTC)及其他需要大量数学计算的算法。保证了在顺序操作下系统工作的实时性需求。这些基于DSP的复杂控制功能、协同控制、通信、标准接口的大量应用使得FPGA控制构架成为了工业多电机高性能驱动领域的理想平台。另外，该系统采用Internet接口与互联网对接，满足未来伺服系统分布式、网络化的发展方向。采用NIOS II或ARM进行多电机任务协同。

为了更好地满足电机的定制式高性能控制，本文采用基于DSP技术的控制策略实现基于物理模型和控制环算法的矢量控制。该项改进能大大缩小电机体积，降低成本和功耗。FOC控制算法通过准确地检测各相电流及电机转速，可以良好地控制电机转速及转矩，使得电机在变载荷环境下也能保持恒转矩输出。图2所示的增强型FOC控制策略，数学模型非常复杂，在电机高速工作时需要很强的运算能力。而基于图4的电机控制系统可实现高实时性的复杂算法运作，并将顶层控制系统集成在单一芯片内，可以通过调节电机性能参数，实现电机驱动的多样化需求。

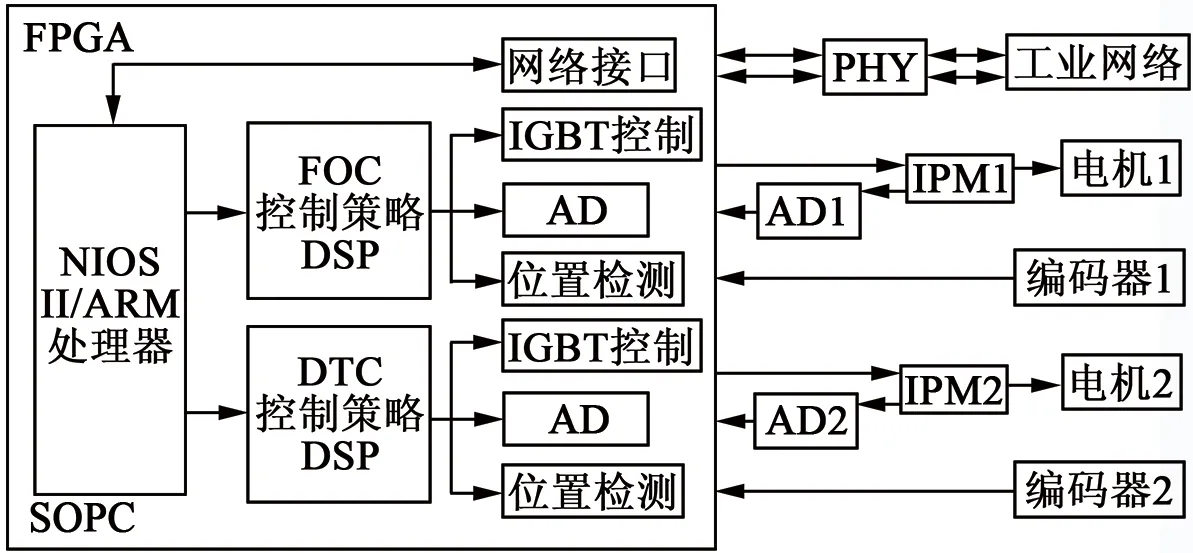
图4 FPGA多电机控制系统结构框图

1.4 多目标规划策略选择

为解决电机在实际工况下的多目标工作需求，分析如图5控制策略与目标关系，对控制模型及工作特性进行观测，寻找各目标随控制参数的关系函数，分配目标权重，建立多目标最优模型。

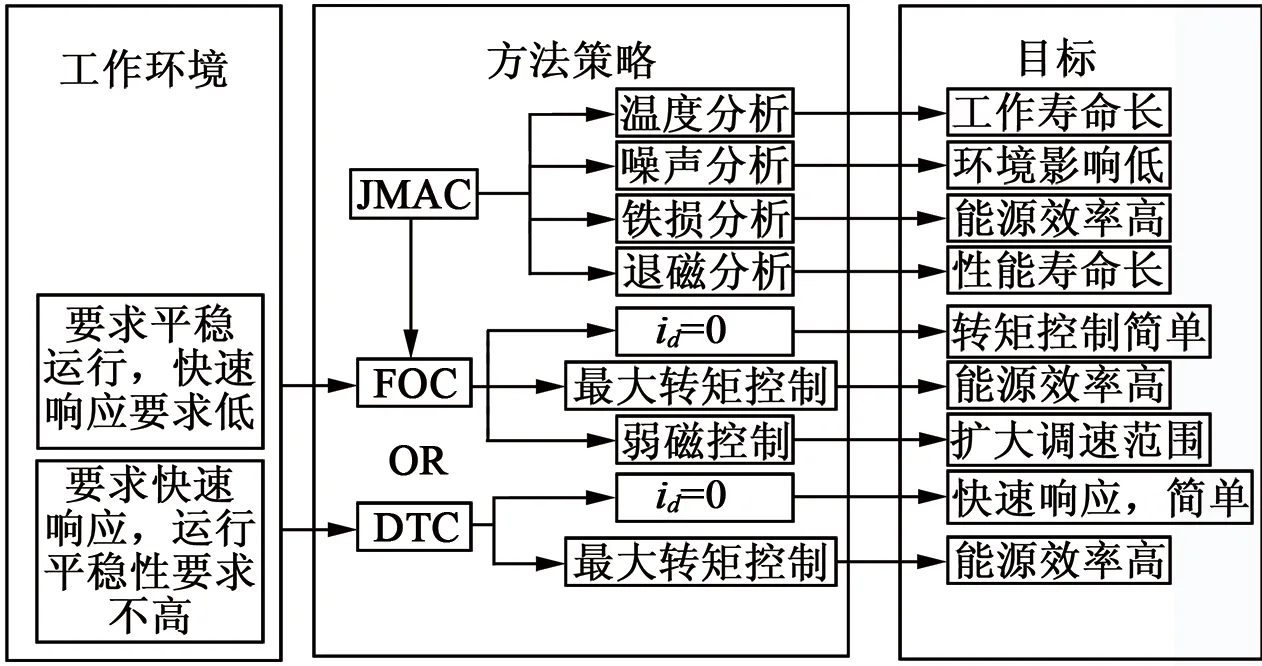
图5 控制策略与目标关系图

minJ=WTeKTe+WopKop+WenKen+WliKli+WevKev

(17)

式中：WTe，Wop，Wen，Wli，Wev分别为最优电磁转矩性能、最优运行状态、最优能源利用、最优寿命、最优环境影响加权系数。KTe，Kop，Ken，Kli，Kev分别为电磁转矩、运行状态、能源利用、寿命、环境影响情况。

2 定制式双目标最优控制算法仿真分析

为了更好地诠释该多目标优化设计的多轴永磁同步电动机控制系统设计方法的可行性，本文建立了以能源效率最高和转矩特性最好为目标的控制系统设计实例。

2.1 JMAG仿真模型搭建

本研究建立以能源效率最高和转矩特性最好为目标的控制系统设计。该实验选择电阻值0.89 Ω、电感0.62 mH、工作电压DC 24 V、功率62 W、额定电流4 A、额定转矩0.2 N·m的永磁同步电动机做为实验电机。

首先在JMAG中依据电机参数，建立几何模型，如图6所示。

图6 JMAG模型及物理场分布云图

将JMAG中模型通过JMAG-RT导入MATLAB当中。建立增强型FOC控制策略模型(如图2所示)。

其次，在MATLAB/Simulink中建立增强型FOC控制策略模型，采用S-function设计控制单元，通过参数化设计的方式快速建模，并以便捷的模块化组合实现控制，为JMAG-MATLAB-Quartus II联合仿真及应用提供坚实基础。

2.2 双目标控制仿真数据分析及参数确定

首先，进行能源利用率最优参数解分析：

1) 对电机能源利用率分析。由于电机无用功损耗主要为铁损，电机铁损主要受电机涡流损耗影响。通过JMAG采集数据分析，电机涡流损耗主要受到电压相位角θ的影响。

2)在实验过程中，我们将MATLAB中建立在2 000～6 000 r/min速度条件下的增强型FOC控制模型导入到JAMG中，经过电机涡流损耗及总能耗的计算，得到电压相位角在90°～180°范围内的电机的功率因数随电压相位变化曲线如图7所示。

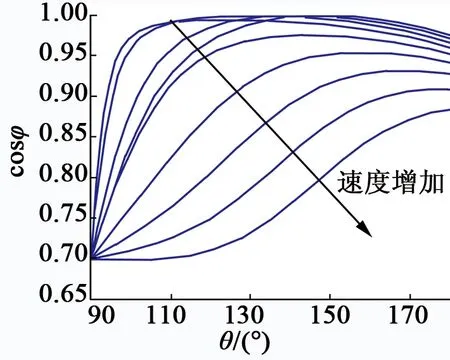
图7 功率因数随电压相位变化曲线

经过对图7功率因数曲线进行分析，可以得到：

1) 在不同速度环境下，电机都有各自对应的最高功率因数相位点。

2) 电机最高功率因数速度点随速度增加由相位角180°不断的向140°移动。

3) 在各相关控制参数相同情况下，电机功率因数随速度的提升不断增加。

为了实现更高的能源利用率，不仅需要寻找各速度点上的最优相位角，而且还应该在控制上保证更高的转矩，使其尽快地进入到高转速目标运行状态。

本台电机的最终目标转速范围在1 000～2 000 r/min之间，我们将实验电机控制目标定为1 500 r/min。在该环境下，得到电机控制的最佳参数为KR=0.63，K2=0.88，Kp1=3.2，Ki1=1.3，Kd1=0.2，Kp2=1.6，Ki2=1.4，Kd2=0.3，Kp3=1.6，Ki3=0.8，Kd3=0.1，电压相位角θ=130°，电流相位角α=95°。当速度在1 500 r/min时，能源利用率可达97.3%。

其次，进行转矩特性最优参数解分析。

1) 利用增强型FOC控制模型，对电机转矩随转矩角α特性进行分析。如图8所示，曲线1为永磁转矩，显然其最大值出现在90°。曲线2为磁阻转矩。由于PMSM中的Ld90°时，磁阻转矩才出现正值。曲线3给出了总转矩，其特性点是α=118°时出现转矩的最大值。为了得到较大的转矩并运行在较高的速度下，PMSM的转矩角一般控制在α>90°的范围内。

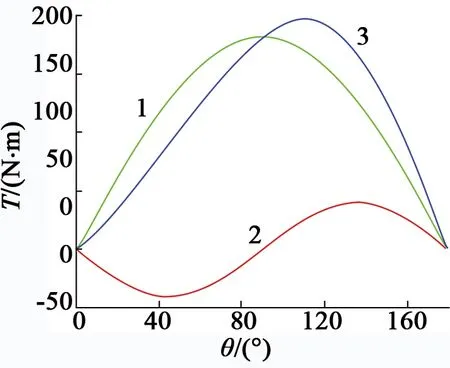
图8 转矩角特性曲线图

2) 由于电机在工作过程转矩需求的不同，在不同转矩下最佳电流相位角有所差异。如图9所示，一方面，电机转矩随电流的增加而不断增加；另一方面，电机的最大转矩负载角随电流的增加，发生微弱的变化。产生一个转矩，存在着不同的电流幅值和负载角。该实验电机设定负载转矩为0.14 N·m,其对应最大转矩负载角则对应为115°。

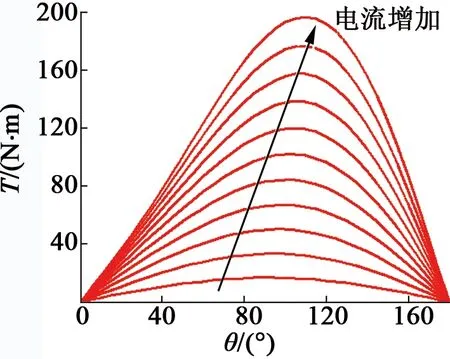
图9 不同电流下的转矩角特性曲线图

3) 以id,iq为变量，针对前述电机参数，采用MATLAB中增强式FOC控制模型，通过JMAG模型仿真计算出电动机转矩后，绘图得出图10。图10中，每一条恒转矩曲线中都存在某一电流与转矩的关系，还在图中画出了4条同心圆曲线。可以发现：在转矩较小时，最小电流的工作点靠近q轴，随着转矩的增加，id分量有明显增大以充分利用磁阻转矩，此时最小电流工作点逐渐偏离q轴。

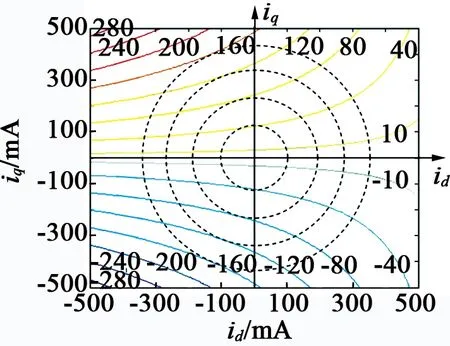
图10 电机转矩与id,iq关系曲线

通过图6我们还可以发现，在第一象限内也可以产生期望的电磁转矩。但是很多显然，一方面电机电流很大，另一方面由于正值id起到加强磁场的作用，所以对应的电动机定制电压会更大，因此基本不会考虑第一象限内的工作点。

通过以上数据，可以在FPGA中通过ROM建立转矩和最小电流关系参数表。而在FPGA中，采用由外界仿真实验得到的数据，通过ROM存储在某目标条件下最优参数的对应关系,可以极大程度地降低芯片计算的工作压力。当采用复杂计算、尤其是sin,cos三角函数计算时，芯片的资源时常超过90%，而使用查找表则可将芯片的资源的使用率降低到30%以下。留下足够的资源为多电机高性能驱动提供设计空间。

经过对增强型FOC控制策略参数变化对转矩性能的分析，我们可以通过上述联合仿真各图中找到，电机转矩性能与交直轴电流及电流相位角参数之间的关系。而电机其他控制参数，如KR，K2等对电机的转矩性能影响较小，主要作用体现在电机稳态性能改进上。通过使用参数KR=0.69，K2=0.73，Kp1=2.8，Ki1=1.1，Kd1=0.4，Kp1=2.7，Ki1=1.5，Kd1=1.3，Kp1=1.9，Ki1=0.5，Kd1=0.1,电流相位角α=115°，可以实现快速达到目标转速并较快的进入稳态。

采用多目标最优模型(式(17))，在本台电机中，我们以能源利用及转矩特性为最优为模型最优目标。设置权重分别为0.7和0.3。以上基于模型的数据测试结果，通过MATLAB拟合函数，建立能源利用率、转矩性能与各项参数的关系函数。得到在目标转速为1 500 r/min下，稳态最优参数解为KR=0.65，K2=0.82，Kp1=3.1，Ki1=1.2，Kd1=0.3，Kp1=2.3，Ki1=1.4，Kd1=0.6，Kp1=1.7，Ki1=0.7，Kd1=0.1，电流相位角α=103°。

最后，根据MATLAB模型仿真得到最优模型控制参数，通过DSP-Builder转入Quartus II中，建立各标准接口及处理控制模型。最终实现高性能多电机FPGA控制器。

由于FPGA是基于电路的硬件描述设计，其各模块间相互独立，并行工作，互不影响。电机数量对电机性能不产生任何影响。可以根据实际情况，参考本文电机控制器目标最优设计流程，实现多目标优化设计的多轴永磁同步电动机控制系统。

该套设计流程完整地对能源效率最高和转矩特性最优的双目标永磁同步电动机控制系统设计方法进行了介绍。多目标优化设计的多轴永磁同步电动机控制系统中其他PMSM则根据实际目标需求，进行多目标优化控制系统设计。

3 系统硬件实验

根据前述理论，设计相关软硬件系统。采用AD7278作为各电机电流检测AD，其工作频率高达48 MHz，可以充分满足高精度采集系统的要求。使用三菱公司生产的PS21767作为IPM驱动器，其PWM开关频率最高可达20 kHz，具有电流、电压、过热保护功能，其最高工作电压可达400 V。使用cyclone IV EP4CE15F17C8 作为FPGA控制芯片，其核心DSP工作频率达到200 MHz，核心计算模块计算延时控制在10 μs内。可以满足多电机10 000 r/min以上、多级数高精度的控制需求。采用Candence进行高速信号完整性分析，保证各路信号的时序约束及抗干扰性能。实验设备如图12所示。

图12 电机控制系统实物图

在实验过程中，将转速目标为1 500 r/min。图13为电机起动后的电机转速检测情况。电机具有较好的启动性能，后期波动较小，在转矩控制上有较好的效果。根据仿真结果，其电机能源利用率(即当前控制策略工作环境下电机的运行效率)达到96.7%。

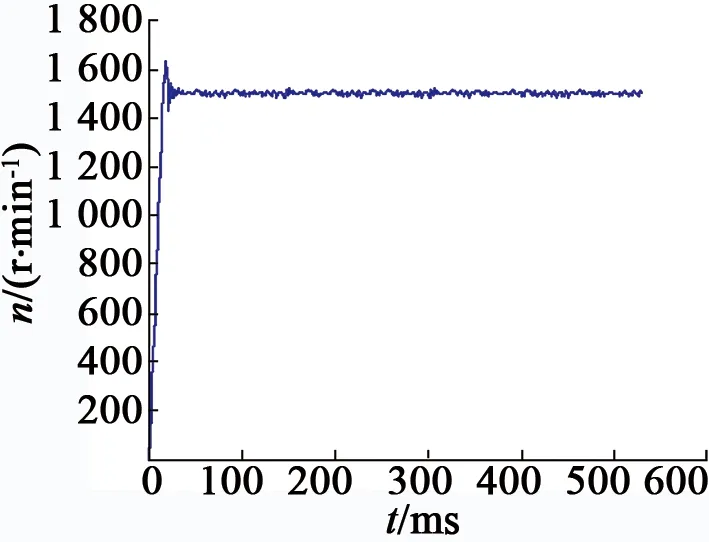
图13 实际编码器测速数据图

4 结 语

本文介绍的基于多目标优化设计的多轴永磁同步电动机控制方法，能较准确地设计出多目标条件下各电机最佳的控制方法。采用FPGA作为多PMSM的控制器，极大降低控制器的设计周期，提高设计灵活度，降低成本，提高稳定性及计算精度等，满足多样化的应用需求。为了更好地展示该目标优化后的控制方法的可行性，本文通过理论仿真与实际实验验证了多目标优化设计及其多PMSM控制的实用性和有效性，并取得良好的控制效果，具有较高的使用价值，在数控机床、机器人等各个定制化需求领域都具有一定借鉴意义。

[1] 寇宝泉，程树康.交流伺服电机及其控制[M].北京：机械工业出版社，2008： 2-4.

[2] GEORGE W Y.Industrial servo control system fundamentals and applications[M].Wisconsin：Marcel Dekker,2013： 78-82.

[3] YUN J M,KO J P,LEE J M.An inexpensive and accurate absolute position sensor for driving assistance[J].IEEE Transactions on Instrumentation and Measurement,2008,57(4)： 864-873.

[4] DEVASIA S.Should model-based inverse inputs be used as feed forward under plant uncertainty[J].IEEE Transactions on Automat Control,2012,47(11)： 1865-1870.

[5] 路甬祥.走向绿色和智能制造-中国制造发展之路[J].电气制造,2012(5):22-24.

[6] 程树康,宫海龙.永磁轮毂电机齿槽转矩研究[J].中国电机工程学报,2009,30(29):47-51.

[7] KURIHARA K,WAKUI,KUBOTA T.Steady-state performance analysis of permanent magnet synchronous motors including space harmonics[J].IEEE Transactions on Magnetics,1994,30(3):1306-1315.

[8] ZHU Z Q,CHEN J T.Influence of stator asymmetry on cogging torque of permanent magnet rushless machines[J].IEEE Transactions on Magnetics,2008,44(11):3851-3854.

Study on PMSM Control System Based on Multi-Objective Optimization

ZHENGBin，WANGMao-sen，DAIJin-song

(Nanjing University of Science & Technology,Nanjing 210094，China)

This paper aims to meet the needs of various types of permanent magnet synchronous motor under different conditions for the diverse needs of the motor performance objectives, and a multi-objective optimal control algorithm design in MATLAB is introduced. By adopting JMAG to realize actual PMSM physical model simulation, a more direct real observations is revealed and the optimal solution is found. Based on the single-chip resource customized FPGA, this paper fulfills the design of high performance multi-axis permanent magnet synchronous motor control system. Thus, in the light of the typical permanent magnet synchronous control experiments of optimal energy efficiency and torque characteristics, the high-performance permanent magnet synchronous motor control system design method proves its superior effect. The research can provide reference for the customized manufacture and high-performance motor control.

multi-axis; PMSM; FPGA; multi-objective optimal; customized; MATLAB; JMAG

2016-05-12

TM341;TM351

A

1004-7018(2016)12-0063-05