空-水冷永磁风力发电机流固耦合仿真

高 俊，孙晓明，郭洪亮，安忠良

(1.沈阳工业大学国家稀土永磁电机工程技术研究中心,沈阳 110870;2.沈阳鼓风机通风设备有限责任公司,沈阳 110022)

空-水冷永磁风力发电机流固耦合仿真

高 俊1，孙晓明2，郭洪亮2，安忠良1

(1.沈阳工业大学国家稀土永磁电机工程技术研究中心,沈阳 110870;2.沈阳鼓风机通风设备有限责任公司,沈阳 110022)

以一台1.65 MW，150 r/min的空-水冷永磁风力发电机为例，建立了电机空-水冷结构的物理模型，采用有限元法对该电机进行了温度场计算，并分析在计算中某些关键参数变化对温度场分析计算的影响规律。通过电机试验，验证所述计算方法的准确性；得出了一些有意义的结论，可为永磁同步风力发电机的设计提供参考。

空-水冷；永磁风力发电机；温度场

0 引 言

目前，风力发电机的发展趋势为单机大容量、高功率密度、低成本和高可靠性。发热问题始终是制约风力发电机发展的首要因素[1-2]。 随着磁负荷和热负荷的也越来越高，温升作为重要性能指标，成为永磁风力发电机设计中需要重点解决的问题[3-7]。

电机温升过高将导致绕组绝缘的损坏，对永磁风力发电机而言，温升过高容易导致永磁体不可逆退磁，上述由温升带来的问题直接影响电机寿命与安全运行。因此，永磁电机中温升的准确计算非常必要[8-10]。

本文以一台1.65 MW，150 r/min的空-水冷永磁风力发电机为例，建立了电机空-水冷结构的物理模型，采用有限元法对该电机进行了温度场计算。通过对计算结果与实验数据的比较分析，验证了计算方法的正确性；得出了一些有意义的结论，可为永磁同步风力发电机的设计提供参考。

1 结构模型

1.1 电机温度场的数学模型

对空水冷结构永磁风力发电机进行三维温度场进行数值研究，根据传热学的基本理论，在直角坐标系下，电机内的稳态温度场三维导热方程可以表示[11]：

(1)

式中：λx，λy，λz为x,y,z方向的导热系数；qv为热源密度；α为电机对流散热系数；Tf为电机周围流体的温度。

根据变分原理，可得等价变分方程:

(2)

对式(2)进行离散化处理，得到的三维温度场有限元方程：

KT=F

(3)

式中：T为求解域内全部节点温度阵列；K，F为总体系数矩阵和总体右端矢量。

1.2 电机流体场数学模型

电机冷却系统中，流体的流动控制方程可表示[12]：

(1)流体质量守恒方程

质量守恒方程：

(4)

式中：ux，uy，uz为在x，y，z方向上速度矢量u的分量。

(2)流体动量守恒方程

动量守恒同样作为流体流动必须遵守的基本方程：

(5)

(6)

(7)

式中：p为流体微元体上的压力。

(3)流体湍流方程

对于不可压缩流体，标准k-ε模型可以表示：

(8)

(9)

(10)

式中：μt为湍动粘度，i，j为下标，i,j=x,y,z且i≠j。

1.3 电机通风冷却结构

本文以一台空-水冷中型异步电机为例进行研究，电机的基本数据见表1。

该电机采用单路轴向冷却通风系统，风罩位于电机外侧，为将冷热风分开，在通风系统中采用隔板。通过风罩上端的两台离心风机向电机内提供冷却气体，冷却气体进入电机后，首先冷却一侧定子线圈端部，然后冷却气体沿轴向流动且分成3路，经由定子铁心背部通风孔、气隙、磁极间隙流向电机另一侧，对电机另一侧线圈进行冷却。由于冷却气体不断与电机内发热构件进行热交换，导致冷却气体温度不断升高，为降低冷却气体的温度，其与风罩上的水冷却器进行热交换，再经由冷却器与风机间的连接管流入风机进入电机内部，形成强迫通风。本文设计的通风系统风路如图1所示。

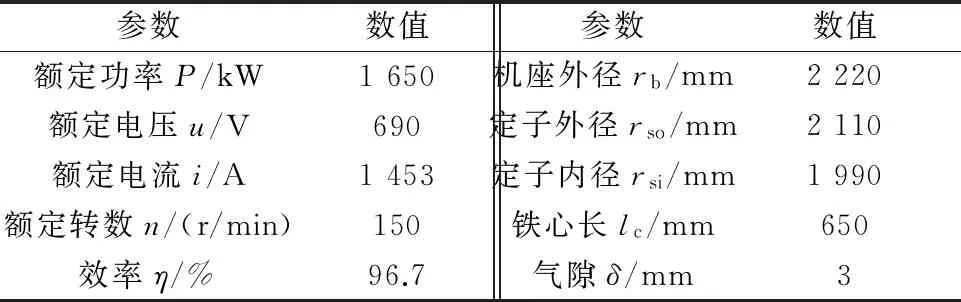
表1 电机基本参数

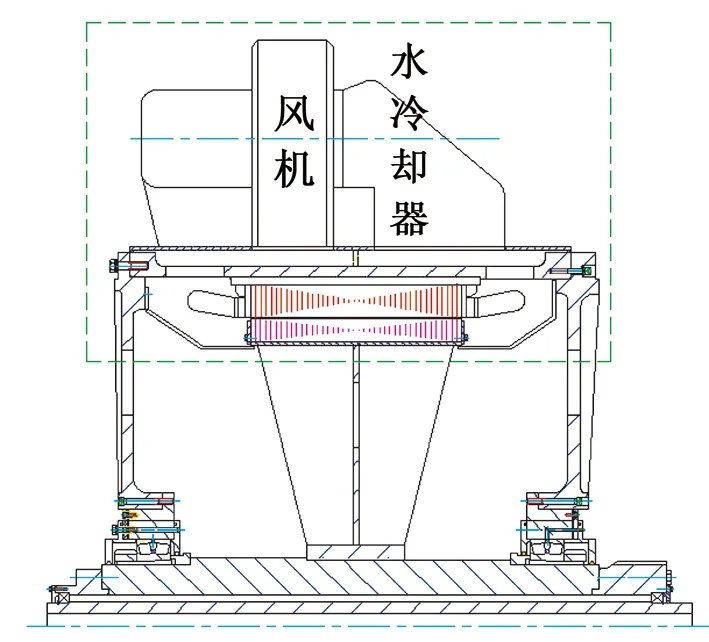
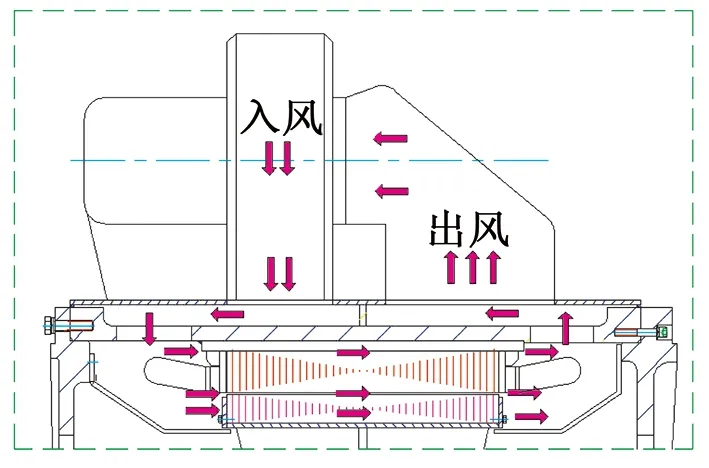
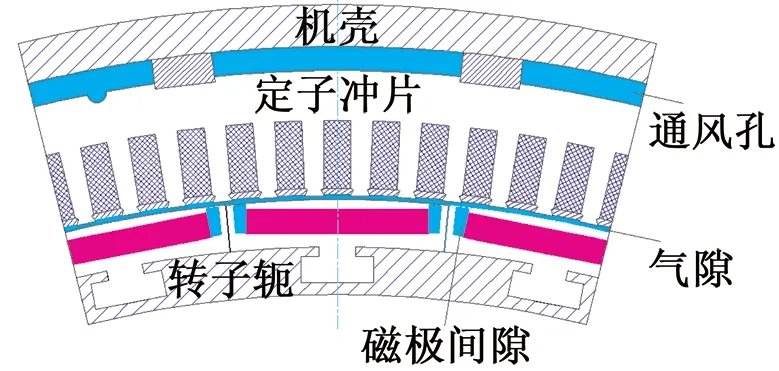
图1 空-水冷却系统

2 基本假设与求解区域的确定

2.1 基本假设与求解区域的确定

基于电机冷却结构以及电机内的流体特性，在温升计算中作出如下假设：(1) 电机稳定运行，冷却系统内风路冷却空气连续、稳定、密闭循环；(2) 空气流动速度远小于风速，即空气马赫数较小，为不可压流体；(3) 空气雷诺数较大，处于湍流状态，计算模型选择标准κ-ε模型。

同样，根据电机结构加上如下边界条件：(4) 考虑对称性，电机取1/6模型。在切面上端盖、机壳、定子部分加对称边界条件，空气部分由于考虑转子旋转的影响，加周期性边界条件；(5) 给定环境温度为27℃(300 K)，转子给定转速150 r/min；(6) 装配间隙选择永磁体和转子铁心间装配间隙为0.2 mm，定子铁心和机壳间装配间隙为0.065 mm。

2.2 求解区域的确定

由于电机模型复杂，计算规模大，取1/6模型为计算对象。计算时考虑了转子旋转的影响。求解区域如图2所示。

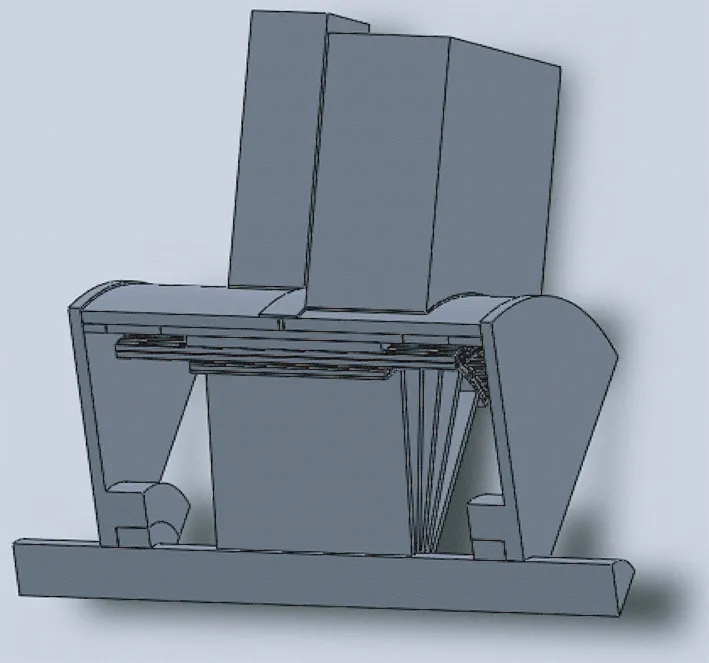
图2 计算模型

3 电机的损耗分布

电机各部分损耗，见表2。

表2 电机各部分损耗

根据电机各部分的实际体积，将各种损耗进行细分，损耗分配如图3所示。

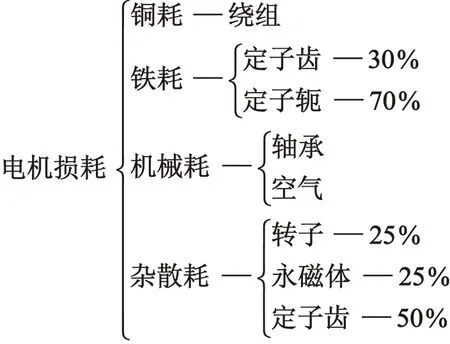
图3 电机各部分损耗分布

其中轴承损耗，可根据式(11)求出：

Pbr=1.03mbn

(11)

式中：n为电机的转速；mb为摩擦力矩。

mb=0.0015GrDsh/2

(12)

式中：Gr为转子重量；Dsh为轴承内圈直径。

除轴承损耗外的机械耗赋给电机内的空气。

电机各部位的生热率，见表3。

表3 电机各部分的生热率

4 仿真分析和实验验证

4.1 流-固耦合温升仿真结果

图4为电机绕组温度分布情况。电机的最高温升为74.5 K，最高温升位置在绕组中间靠近驱动侧出风口的位置，这是由于绕组端部位置受到冷却风的吹拂而易于散热。绕组在非驱动侧靠近机壳入风口的位置温升较低，最低温升为45.8 K。绕组的平均温升约为60 K。

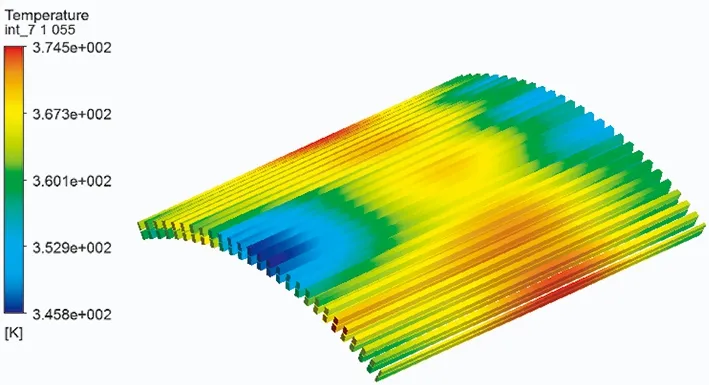
图4 电机绕组温升分布

图5为算得电机整机温度分布(包括气体部分)。从图中可以看出，冷却气体流出电机时温升约为20 K，且由于受到转子旋转的影响，出风口处冷却气体存在旋流现象。

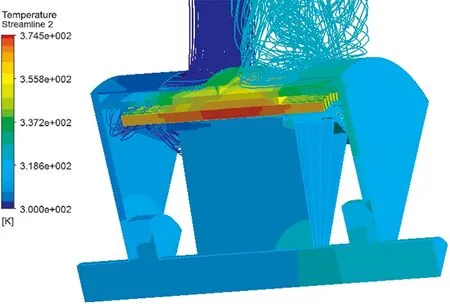
图5 整机温升分布

4.2 计算结果与试验数据对比

表4所示计算结果与试验数据的对比。

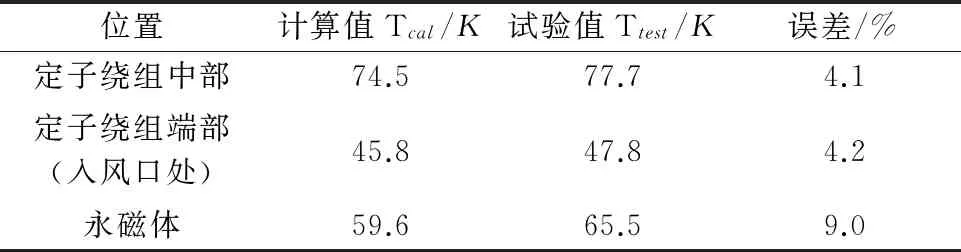
表4 温升计算结果对比

由表4可知，定子绕组温升计算结果与试验结果基本吻合，误差仅为4%。永磁体温升计算值与试验值误差为9.0%，相差约6 K，分析是由于流-固耦合计算时，转子幅板建成了等宽直板，加强了转子散热能力，而实际设计中越靠近轴的位置越窄，与实际设计相比转子散热容易，故而实际永磁体的温升略高于计算值。

4.3 电机通风位置的变化对电机的影响

本文分析了不同出、入风口位置变化时，系统流速及温度的变化情况。在计算时保证孔出、入风口的面积、系统的总流量不变。电机不同出入、风口的排布情况，如图6～图9所示。其中径向位置指出、入风口设置在机壳圆周上；轴向位置指出、入风口设置在端盖侧方。

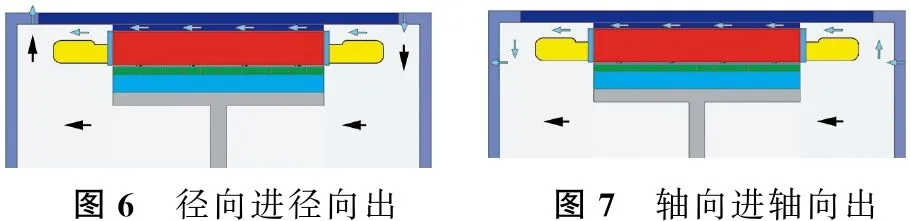
图6 径向进径向出图7 轴向进轴向出

图8 径向进轴向出图9 轴向进径向出

电机采用不同进出口位置时各部分的流速分配如图10所示。由图10可以看出，四种不同情况变化，对定子通风孔流速的影响很小，均保持在18 m/s，而气隙与极间间隙处的流速分别为9.15 m/s，8.79 m/s，8.68 m/s和8.47 m/s，最大风速差别为7.4%。

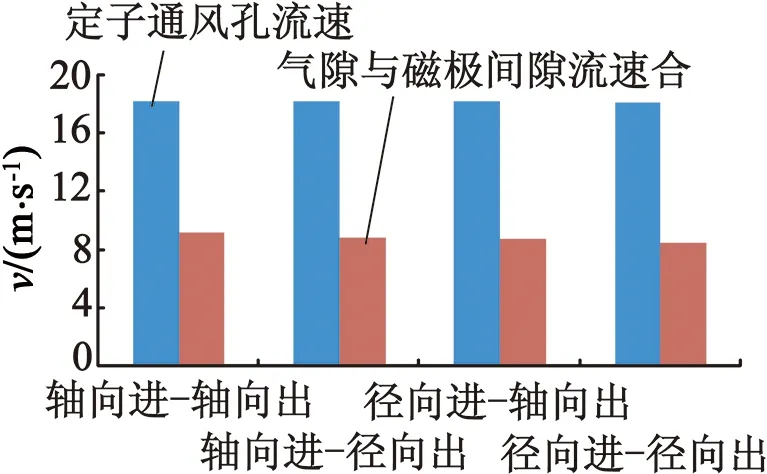
图10 不同通风位置电机的流速分配情况

图11所示为不同通风位置时，电机永磁体及定、转子表面的温升变化情况。可以看出，通风位置变化时，电机各部分的温升逐渐升高。其中永磁体的温升分别为48.7 K，51.5 K，56.4 K和59.6 K，温升最大差别为18.7%。转子外表面的温升分别为48.6 K，51.4 K，56.3 K和59.5 K，温升最大差别为18.3%。定子内表面的温升分别为55.3 K，58.9 K，59.9 K和64.0 K，温升最大差别为13.5%。

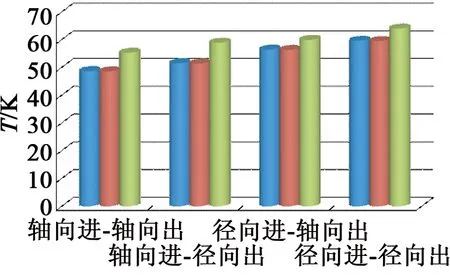
图11 不同通风位置电机气隙处的温度分布

从以上计算可以看出，由于定子通风孔风阻远小于气隙，出入风口的位置变化并不会改变风量主要从定子通风孔中流过的流量分布状态，定子通风孔风速变化较小。但对于流截面较小的气隙位置，总风量分配的微小改变会较为显著地影响其流过的冷却风流量及其流速，影响转子部分的散热效果。此时，气隙冷却风的减少直接造成转子散热困难、温升升高，并且有更多的转子热量需要通过定子散出，同时造成温升升高的结果。

4.4 不同流量分配对电机温升的影响

定子通风孔高度变化影响电机通风系统在发电机内部的风量分配。为了使电机冷却系统达到最优，实现电机内各部分风量的合理分配，本文对不同通风孔尺寸进行比较分析，分析过程中，保持系统总风量不变，分析结果见表5。

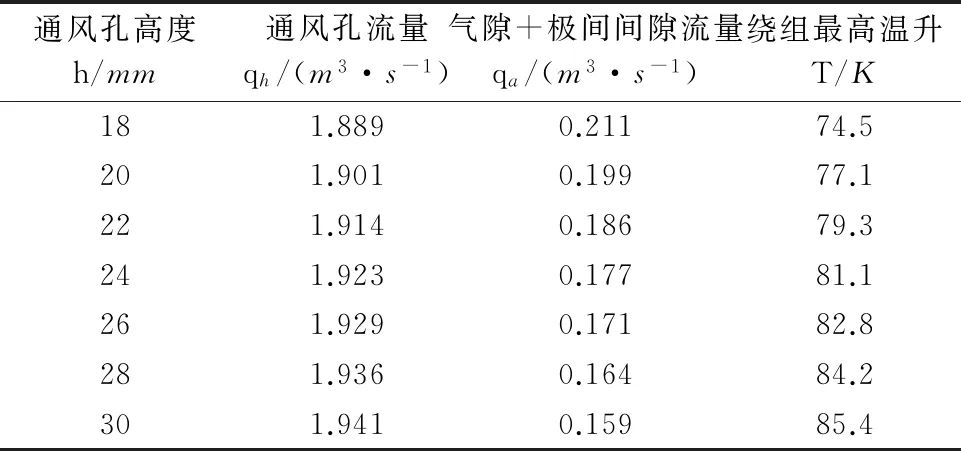
表5 不同流量分配对绕组温升的影响

由表5可知，当通风孔尺寸逐渐增大时，定子通风孔流量随之增大，但其增加速度小于通风孔过流面积的增加速度，因此通风孔内的风速降低。同时气隙和极间间隙中的流量也逐渐减小，但其过流面积没有变化，其风速亦降低，从而系统的冷却能力降低，绕组的温升逐渐升高。

5 结 语

本文对以一台1.65 MW，150 r/min的空-水冷永磁风力发电机双转子电机进行了流-固耦合分析，得到以下结论：

1) 通过温度场分析计算可以得出该结构电机的最高温升出现在绕组中间靠近驱动侧出风口的位置，绕组最低温升出现在入风口的位置。绕组最高温升和最低温升差别高达38.5%。

2) 不同通风位置改变，对定子通风孔内风速影响较小。但对于流截面较小的气隙位置，通风位置的改变会较为显著地影响其流过的冷却风流速，由径向通风改为轴向通风，气隙位置风速可增加10%左右。

3) 电机温升的计算结果与试验结果基本吻合，论证了本文所采用的求解模型及计算方法正确。

[1] 唐任远,赵清,周挺.稀土永磁电机正进入大发展时期[J].沈阳工业大学学报,2011,33(1):1-8.

[2] 程明,张运乾,张建忠.风力发电机发展现状及研究进展[J].电力科学与技术学报,2009,24(3):2-9.

[3] 张岳，王凤翔．直驱式永磁同步风力发电机性能研究[J]．电机与控制学报，2009，13(1):78-82．

[4] 温志伟，顾国彪．实心磁极同步电动机转子温度场计算[J]．大电机技术，2005(2):1-5．

[5] 姚若萍，饶方权．蒸发冷却水轮发电机定子温度场研究[J]．中国电机工程学报，2003，23(6):87-90．

[6] BOGLIETTI A，CAVAGNINO A，LAZZARI M， et al． A simplified thermal model for variable-speed self-cooled induction motor[J]．IEEE Transactions on Industry Applications，2003，39(4):945-952．

[7] 黄学良，胡敏强，周鹗．电机三维温度场新的有限元模型[J]．中国电机工程学报，1998，18(2):78- 82．[8] 李伟力,李勇,杨雪峰,等.大型空冷汽轮发电机定子端部温度场与流体场的计算与分析[J].中国电机工程学报,2009,29(36):80-87.

[9] 李伟力,陈玉红,霍菲阳.大型水轮发电机转子旋转状态下磁极间流体流动与温度场分析[J].中国电机工程学报,2012,32(9):132-139.

[10] 丁舜年.大型电机的发热与冷却[M].北京:机械工业出版社,1998.

[11] 胡田,唐任远,李岩,等.永磁风力发电机三维温度场计算及分析[J] .电工技术学报,2013,28(3):122-126.

[12] 王福军.计算流体动力学分析—CFD软件原理与应用[M].北京：清华大学出版社,2004.

Thermal Analysis and Calculation for Air-Water Cooled Permanent Magnet Wind Generators

GAOJun1，SUNXiao-ming2，GUOHong-liang2，ANZhong-liang1

(1.Shenyang University of Technology National Engineering Research Center for Rare-earth Permanent Magnet Machines,Shenyang 110870,China;2.Shenyang Blower Works Group Co.,Ltd.,Shenyang 110022,China

An 1.65 MW, 150 r/min of air-water cooled permanent magnet wind generator was built in the experiments. The physical model of motor with air-water cooling structure was established. The temperature of the motor was calculated by finite element method. The influence of some key factors on temperature was analyzed. According to the comparing of the calculated results and experimental data, verifies the correctness of the calculation method and some meaningful conclusions are obtained. It is the reference for the design of permanent magnet synchronous generator.

air-water cooling; permanent magnet wind generator; thermal field

2016-05-13

刘细平(1976-)， 男，博士，教授，研究方向为稀土永磁电机设计、风力发电及其相关控制。

TM315；TM351

A

1004-7018(2016)12-0020-04