FIR滤波器的等波纹最佳逼近法优化设计

蔚瑞(渤海大学 辽宁 锦州 121000)

FIR滤波器的等波纹最佳逼近法优化设计

蔚瑞
(渤海大学 辽宁 锦州 121000)

本文针对窗函数设计法和频率采样法在FIR滤波器设计中存在较大的资源浪费的问题提出采用等波纹最佳逼近法进行优化，并且采用MATLAB编程对窗函数设计法和该方法进行比较以求能直观地验证其优越性。

FIR滤波器优化设计；等波纹最佳逼近法；MATLAB仿真

1.引言

在现代信号处理中，例如图像处理、数据传输、雷达接收以及一些要求较高的系统对相位要求较为严格所以通常采用有限冲激响应滤波器即FIR滤波器。设计该滤波器的方法一般有窗函数设计法和频率采样法，虽然它们简单方便，易于实现但都有缺点，总的来说是所设计的滤波器性价比低，所以FIR数字滤波器的最优化设计就显得格外重要。

2.FIR数字滤波器的优化设计

2.1 优化设计准则

优化设计有以下三种方法：均方误差最小化准则、最大误差最小化准则和切比雪夫最佳一致逼近。其中均方误差最小准则就是选择一组时域采样值，以使均方误差最小。这一方法注重的是在整个-π～π频率区间内总误差的全局最小，但不能保证局部频率点的性能，有些频点可能会有较大的误差。最大误差最小化准则（也叫最佳一致逼近准则）是通过改变N个频率采样值（或时域h（n）值），使频响误差在给定频带范围内最大逼近误差达到最小。

2.2 等波纹最佳逼近法

2.2.1含义及优点 使用的最佳化准则是“最大误差最小化准则”，所谓的等波纹是指用此方法设计的FIR数字滤波器的幅频响应在通带和阻带都是等波纹的，而且分别控制通带和阻带波纹幅度。最佳逼近是指在滤波器长度给定的条件下，使加权误差波纹幅度最小化。优点：阶数相同时，使滤波器的最大逼近误差最小，也就是通带最大衰减最小，阻带最小衰减最大；指标相同时，可使滤波器阶数最低。

2.2.2基本思想 等波纹最佳逼近基于切比雪夫逼近，在通带和阻带以|E(ω)|的最大值最小化为准则，采用Remez多重交换迭代算法求解滤波器系数h（n）。定义加权误差函数E（ω）为

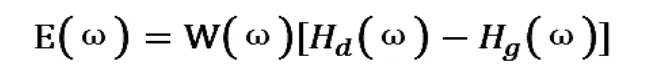
其中W(ω)称为误差加权函数，用来控制不同频段（一般指通带和阻带）的逼近精度。表示希望逼近的幅度特性函数，设计线性相位FIR数字滤波器时必须满足线性相位约束条件，表示实际设计的滤波器幅度特性函数。

在此方法设计中，把数字频段分为“逼近（或研究）区域”和“无关区域”。逼近区域通常指通带和阻带，而无关区域一般指过渡带。设计过程中只考虑对逼近区域的最佳逼近，但是无关区宽度不能为零，即不能是理想滤波特性。用等波纹最佳逼近法设计FIR数字滤波器的步骤为：

根据给定的逼近指标估算滤波器阶数N和误差加权函数W(ω)；

采用remez算法得到滤波器单位脉冲响应h(n)。

3.计算机模拟

3.1 已有的编程工具

MATLAB信号处理工具箱函数中为我们提供了采用经典窗函数法设计线性相位FIR数字滤波器的函数即fir1且具有标准低通、带通、高通，带阻等类型。其调用格式及功能如下：

• hn=fir1(M，wc)，返回6dB截止频率为wc的M阶（单位脉冲响应h（n）长度N=M+1）FIR低通（wc为标量）滤波器系数向量hn，默认选用汉明窗。滤波器单位脉冲响应h(n)和向量hn的关系为：h（n）=hn（n+1） n=0，1，2，…，M。而且满足线性相位条件：h（n）=hn（N-1-n），其中wc是对π归一化的数字频率，0≤wc≤1。

当wc=[wcl，wcu]时，得到的是带通滤波器，其-6dB通带为wcl≤ω≤wcu。

• hn=fir1(M，wc，‘ftype’)，可设计高通和带阻FIR滤波器。当ftype=high时，设计的是高通滤波器；当ftype=stop，且wc=[wcl，wcu]时，设计的是带阻滤波器。在设计高通和带阻FIR滤波器时，阶数M只能取偶数（h（n）长度N=M+1为奇数）。不过，即使用户将M设置为奇数时，fir1也会自动对M加1。

hn=fir1(M，wc，window)，可以指定窗函数向量window。如果缺省window参数则默认为汉明窗。

hn=fir1(M，wc，‘ftype’，window)，通过选择wc，ftype和window参数可以设计各种加窗滤波器。

而remez和remezord是用来实现线性相位FIR数字滤波器的等波纹最佳逼近设计的MATLAB信号处理工具箱函数。下面介绍这两种函数的调用格式和功能：

remez

remez函数实现线性相位FIR数字滤波器的等波纹最佳逼近设计。其调用格式有以下几种分别为：

•hn=remez（M，f，m，w）%最常用的格式

调用结果返回单位脉冲响应向量hn。remez函数的调用参数（M，f，m，w）一般通过调用remezord函数来计算。调用参数含义为：M为FIR数字滤波器阶数，hn 长度N=M+1。f是边界频率向量，0≤f≤1，要求f为单调增向量（即f（k）< f（k+1），k=1，2，…），且从0开始，以1结束，1对应数字频率ω=π（模拟频率，表示时域采样频率）。m是与f对应的幅度向量，m与f长度相同，m（k）表示频点f（k）的幅度响应值。f和m给出希望逼近的幅度特性，w是误差加权向量。

•hn=remez(M，f，m)

设计一个M阶FIR数字滤波器，其频率响应在数组f 和m中给定，含义与上述情形相似，只是数组w中的值均为1。

•hn=remez（M，f，m，w，ftype）

含义与上述情形均类似，只有当ftype是字符串“hilbert”或“differentiator”时，它相应地设计数字希尔伯特变换器或数字微分器。

对于数字希尔伯特变换器，数组f中的最低频率不能等于0，最高频率不能等于1；而对于数字微分器来说，矢量m不给出每个带中预期的斜率，而是给出预期的幅度。

remezord

remezord函数可根据逼近指标估算等波纹最佳逼近FIR数字滤波器的最低阶数M、误差加权向量w和归一化边界频率向量f，使滤波器在满足指标的前提下造价最低。其返回参数作为remez函数的调用参数。其调用格式为：

[M，fo，mo，w]=remezord(f，m，rip，Fs)

参数含义说明:f与remez中的类似，这里f可以是模拟频率（单位是Hz）或归一化数字频率，但必须从0开始，到（用归一化频率对应1）结束，而且其中省略了0 和两个频点。为采样频率，缺省时默认=2Hz。但是f的长度（包括省略的0和两个频点）是m的两倍，即m中的每个元素表示f给定的一个逼近频段上希望逼近的幅度值。rip表示f和m描述的各逼近频段允许的波纹幅度（幅频响应最大偏差），f的长度是rip的两倍。

所以，调用这两个函数设计线性相位FIR数字滤波器的关键在于要根据设计指标求出remezord函数的调用参数f、m、rip和。

3.2 编程验证

以设计FIR数字低通滤波器为例，相应的指标为：

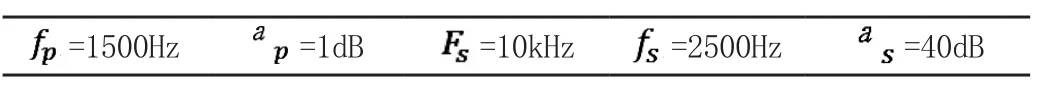
其中含义如下：

首先对所需指标进行估算可以得到：选择凯塞窗可以降低滤波器阶数。

3.2.1使用凯塞窗设计的MATLAB程序如下：

fp=1500；fs=2500；rs=40；Fs=10000；

wp=2*pi*fp/Fs；ws=2*pi*fs/Fs；

Bt=ws-wp； %计算过渡带宽度

alph=0.5842*(rs-21)^0.4+0.07886*(rs-21)； %计算kaiser窗的控制参数a

M=ceil((rs-8)/2.285/Bt)； %计算kaiser窗所需阶数M

wc=(wp+ws)/2/pi；

hn=fir1(M，wc，kaiser(M+1，alph))；%调用kaiser计算低通FIRDF的h（n）

运行结果如下图：

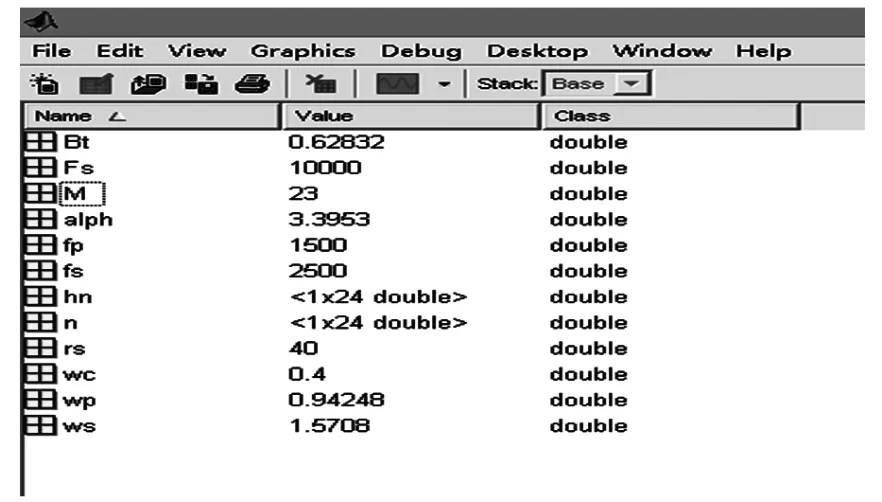
可以看到M=23即使用kaiser窗设计的滤波器阶数为23。

3.2.2使用等波纹最佳逼近法设计的MATLAB程序如下：

Fs=10000；f=[1500，2500]；m=[1，0]；

rp=1；rs=40；

dat1=(10^(rp/20)-1)/(10^(rp/20)+1)；

dat2=10^(-rs/20)；

rip=[dat1，dat2]；

[M，fo，mo，w]=remezord(f，m，rip，Fs)；%边界频率为模拟频率（Hz）时必须加入采样频率

M=M+1； %估算的M值达不到要求，加1后满足要求

hn=remez(M，fo，mo，w)；

运行结果如下图：

可以看到M=15即使用等波纹最佳逼近法设计的滤波器阶数为15。

综上，我们可以从MATLAB编程运行的结果直观地看到：指标相同时，即使用等波纹最佳逼近法设计可使滤波器阶数明显降低。

3.2.3同时用窗函数和等波纹最佳逼近设计相同阶数的FIR数字滤波器

以设计一个20阶FIR低通滤波器为例，要求如下：

MATLAB程序如下：

fp=1500；fs=2500；Fs=10000；

wp=2*pi*fp/Fs；ws=2*pi*fs/Fs；

M=20；n=M+1；

wc=(wp+ws)/2/pi；

hn1=fir1(M，wc)；% 默认采用汉明窗设计滤波器

[h，w1]=freqz(hn1)；%计算滤波器的频率响应

f=[0，0.3，0.5，1]；

m=[1，1，0，0]；

hn2=remez(M，f，m)；%采用remez设计滤波器

[hh，w2]=freqz(hn2)；%计算滤波器的频率响应

figure(1)

plot(w1/pi，abs(h)，w2/pi，abs(hh)，f，m)；grid on%绘制滤波器幅频响应

legend('fir1'，'remez'，'理想特性')；%给出图例

xlabel('w/pi')；ylabel('幅度')

figure(2)

plot(w1/pi，20*log10(abs(h))，w2/pi，20*log10(abs(hh)))； %绘制损耗函数

grid on

legend('fir1'，'remez')；%给出图例

xlabel('w/pi')；ylabel('幅度/dB')

figure(3)

impz(hn1，n)；grid on%绘制单位脉冲响应

xlabel('n')；

ylabel('h(n)')

figure(4)

impz(hn2，n)；grid on%绘制单位脉冲响应

xlabel('n')；

ylabel('h(n)')

程序运行后可得：

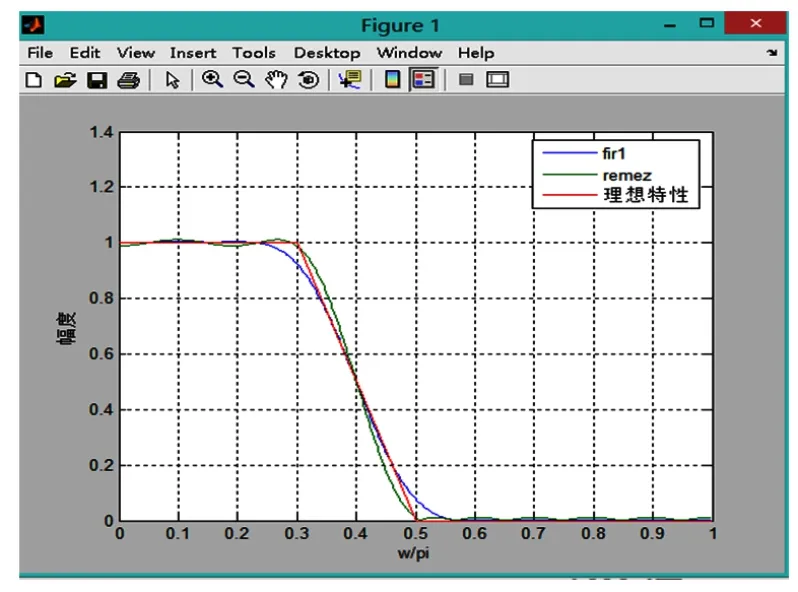
幅频响应损耗函数

结论：从幅频响应可以直观地看到用等波纹最佳逼近法设计FIR低通滤波器相较窗函数设计法更接近于理想特性。但是由于remez要求等波纹的特点，其在通带内的振动幅度较大；由损耗函数可以清楚地看出阻带的波纹变化曲线，remez接近等波纹，而fir1的振动幅度较大。并且比较窗函数设计法和等波纹最佳逼近法的滤波器指标可以看到，前者的过渡带宽较宽，通带最大衰减较小。

4.结束语

通过MATLAB仿真来直观地验证了使用等波纹最佳逼近法设计FIR滤波器时可以达到在指标相同时阶数最低，而阶数相同时滤波器的最大逼近误差最小，所以等波纹最佳逼近法在FIR滤波器的设计中有重要意义。

[1]高西全，丁美玉．数字信号处理(第三版)[M]．西安:西安电子科技大学出版社，2008.8

[2]万永革.数字信号处理的MATLAB实现[M].北京：科学出版社，2007

[3]张德丰.MATLAB数字信号处理与应用[M].北京：清华大学出版社，2010.1

TP3

A

1009-5624（2016）06-0045-04