基于支持向量机的NBA季后赛预测方法

曾　磐，朱安民

深圳大学计算机与软件学院，广东深圳 518060



Received：2015-10-03；Accepted：2015-12-10

Foundation：National Natural Science Foundation of China(61273354)

† Corresponding author：Professor Zhu Anmin. E-mail: azhu@szu.edu.cn

Citation：Zeng Pan, Zhu Anmin. A SVM-based model for NBA playoffs prediction[J]. Journal of Shenzhen University Science and Engineering, 2016, 33(1): 62-71.(in Chinese)

【电子与信息科学 / Electronic and Information Engineering】

基于支持向量机的NBA季后赛预测方法

曾磐，朱安民

深圳大学计算机与软件学院，广东深圳 518060

摘要：通过对参加NBA赛事的每支球队在常规赛阶段的数据统计，整合出球队常规赛综合得分、球员常规赛综合得分、主教练水平及主客场因素4项指标作为一支球队的综合实力体现，构建训练样本，使用适合小样本数据的基于结构风险最小化的支持向量机(support vector machine, SVM)来训练一个预测模型，并预测NBA季后赛每场比赛的胜负．通过结合欠采样和过采样技术消除训练样本中的不平衡数据，更好地发挥SVM的学习能力．实验表明，所提方法具有较好的预测效果．

关键词：计算机感知；NBA季后赛；因子分析；支持向量机；不平衡数据；欠采样；过采样

美国及加拿大职业篮球联盟(National Basketball Association，NBA)从1946年创办以来已发展成为一个集体育运动和娱乐消费于一体的大型商业集团，将篮球文化推向了一个新的高度．NBA的数据系统对比赛的量化程度让人惊叹，NBA从来都是依靠前沿的技术作支持，同时为比赛预测和比赛分析提供了大量的数据基础．NBA的比赛精彩刺激，每支球队之间的实力差距都不大，每场比赛都充满无限可能，这使预测比赛成为一项富有挑战且有意义的事情．Melnick[1]分析了1993—1998各年度赛季的常规赛数据，发现球队胜率与球队助攻之间存在正相关．勒勇[2]对2005—2006赛季总决赛球员的季后赛表现进行了分析，发现总决赛制胜的3个因素为：战术的发挥水平、超级球星的数量和质量、主教练的总决赛经验和心理调节能力．邱胜等[3]分别对2004—2005和2006—2007的季后赛建立Logistic和Bayes预测模型，发现球队常规赛综合水平和超级明星数量以及主教练常规赛和季后赛的执教经验决定了季后赛比赛胜负．Chatterjee等[4]对NBA所有球队一个赛季的数据建立统计模型，对球队胜率进行回归分析，发现得分、罚球、篮板和失误在统计上具有显著性，且回归系数在各年数据之间都是相对稳定的．由于赛事瞬息万变，影响比赛胜负的因素诸多，所以研究人员只能相对尽可能多地找到影响比赛胜负的因子，并合理地组织使其成为适合预测的形式．

本研究根据NBA球队常规赛的数据统计来预测其季后赛的表现．因为漫长的82场常规赛可基本展示出一支球队的综合实力，本研究提取常规赛数据中影响球队综合实力的特征组成一个合理的样本空间，并采用基于结构风险最小化的支持向量机(support vector machine, SVM)来训练一个预测模型．目前使用SVM进行预测的研究有很多，如倪建军等[5]用SVM作为预测模型并配合基于核的主成分分析(kernel principal component analysis, KPCA)方法在复杂的水资源环境系统下建立了一个突发污染事件的监测系统； Torheim等[6]使用磁共振动态增强扫描(dynamic contrast-enhanced magnetic resonance imaging, DCE-MRI)扫描获取的宫颈癌病人白利糖度的药代动力学模型参数，经过纹理分析后和一些临床因素一起作为特征训练了一个SVM分类器来预测宫颈癌病人的治疗效果．SVM对不平衡数据样本较敏感，而NBA季后赛的比赛结果常常是不平衡的，即主场优势球队胜场多于主场劣势球队，所以本研究还采用了两种特定的算法对数据做了平衡化处理，使样本空间更适于SVM建立预测模型．查阅大量文献，尚未发现有人使用SVM作为模型来预测NBA比赛结果的，也未见有对球赛预测数据进行过平衡化处理的研究．本研究首先定义了采集数据的内容及处理方法，在数据层面进行平衡化处理，再使用SVM对平衡化后的数据建立预测模型，并通过实验证明其性能可观．

1数据构成

1.1数据采集

本研究分析的数据均采自NBA统计网站www.stat-nba.com，采集了2003—2015共13个赛季每支季后赛参赛球队的常规赛数据．每个赛季每支季后赛参赛球队的具体采集内容见表1．由于直接采集的球队相关数据项很多，不便直接构建训练样本进行分析，因此根据球队各个指标的特性将所有指标转换为4项综合指标以便构建训练样本集．本研究设计的样本数据包括球队常规赛综合得分、球员常规赛综合得分和主教练水平及球队主客场影响3部分．

1.2球队常规赛综合得分

NBA数据专家Oliver[7]提出了一个满分为100分的计算一支球队综合实力得分的公式

score_Oliver=0.5×{[t3+0.4t7-1.07t9/(t9+

o10)×t3×(1-t2)+t14]+[o3+

0.4o7-1.07o9/(o9t10)×o3×

(1-o2)+o14]}

(1)

根据式(1)可计算一个球队常规赛综合得分， 求出score_Oliver对于球队胜场的相关系数r=-0.136．

本研究提出另一种球队常规赛综合得分的计算方式，采用因子分析的方法对球队实力进行评价．首先对表1中的指标a1～a16按最大方差旋转法作因子分析，取累计贡献达到80%的m个因子向量Fi(i=1,2,…,m)来解释球队指标，取每个因子的方差贡献作为其权重wi(i=1,2,…,m)， 定义新的球队常规赛能力值计算公式为

scoure_factors=∑factor_scorei×wi

(2)

其中，factor_scorei是Fi的因子得分．这里对原数据的p1～p16指标作因子分析，取累计贡献率达82.3%的前7个因子向量，采用最大似然来估计因子的载荷阵并用加权最小二乘估计来计算因子得分(本研究使用Matlab自带的factoran函数对源数据作因子分析)，得到的载荷阵和因子权重见表2．

表1　单赛季每支球队数据指标

根据观察各个因子的载荷可以发现： F1主要反映球队的进攻能力； F2反映球队在比赛中失误的情况； F3反映球队防守能力； F4反映了球队制造犯规的能力； F5反映球队的进攻欲望； F6反映了球队的稳定性．根据式(2)计算出192支季后赛球队综合得分，求出score_factors对于球队胜场t1的相关系数r=0.664．

本研究对原数据的a1～a16指标进行主成分分析，选择降为6维．此时的球队常规赛得分

score_PCA=finaldata×selectedvalues

(3)

其中，finaldata是经过主成分分析处理降维后的数据；selectedvalues是最大的6个特征值．根据式(3)计算出的192支季后赛球队综合得分，求出score_PCA对于球队胜场的相关系数r=0.897．

至此，关于球队常规赛综合得分已有3种数据，这里分别称其为Oliver数据、因子分析数据以及PCA数据．它们对球队常规赛胜场数的相关性依次递增，而一支NBA球队的综合实力并非仅仅由常规赛胜场数来决定．因此本研究偏向用因子分析数据作为球队常规赛综合得分来构成最后的样本数据．

表2　旋转因子载荷阵与权重

1.3球员常规赛综合得分

NBA数据分析专家Hollinger定义了一项球员综合实力计算公式，可综合反映一个球员在当赛季对球队各方面的贡献，计算公式[7]为

player_score=p1+0.4p2-0.7p3-0.4(p4-p5)+

0.7p6+0.3p7+p8+0.7p9+0.7p10-

0.4p11-p12

(4)

通常每支球队的12人阵容名单中会有1～2名核心球员，正是这几名核心球员代表了球队阵容的实力．核心球员人数通常约占球队总人数的10%，根据式(4)计算出每个赛季球队所有球员的综合得分，然后选出每个赛季前10%的球员作为核心球员，并以得分最低的那名核心球员的得分作为核心球员和非核心球员的分水岭m． 球队中得分超过m的球员定义为核心球员，依此标准选出每支球队的核心球员数量n． 如果球队中没有得分超过m的球员则选择该队得分最高的球员作为核心球员．然后计算每支球队的核心球员得分总和sum=∑player_scorei． 本研究用(n,sum)这种二维数据来表示球员常规赛能力值水平．

例如，在2013—2014赛季是否核心球员的分水岭m=14.68，得分超过这一数值的球员为球队的核心球员．筛选出的核心队员均是一些大家耳熟能详的明星球员，如热火队的勒布朗詹姆斯和德怀恩韦德，得分分别为22.71和14.82；雷霆队的凯文杜兰特和维期布鲁克，得分分别是21.12和19.77；快船队的布雷克格里芬和克里斯保罗，得分分别是18.88和19.87．

1.4主教练水平

主教练的执教水平可以由过去所执教比赛的胜率和执教比赛场次来综合体现．本研究截选每个球队主教练从其执教生涯开始到当赛季为止以往的常规赛执教总场数(c1)， 常规赛执教总胜率(c2)， 季后赛执教总场数(c3)以及季后赛执教胜率(c4)这4个指标来评估球队主教练的水平．对于每个赛季的每支球队，均选取该球队参加季后赛时的主教练数据作为球队的主教练水平．

1.5球队主客场因素

一般在NBA的比赛中主场球队的取胜概率要高于客场球队．而季后赛系列赛采用7场4胜制．对阵双方球队中常规赛战绩较好的球队最多有4个主场，而对手最多只有3个，因此有一方球队拥有主场优势．本研究通过球队在常规赛主客场的表现来度量季后赛中的主场优势以及客场劣势，用wh表示一个球队常规赛在主场的胜率，用la表示该球队在客场的输率，并定义变量home_ad来度量主场优势．

1.6数据组织

此时对于每个赛季的每支球队构建了一个由球队常规赛综合得分，球员常规赛综合得分，主教练水平以及主客场影响4个部分组成的数据．表3展示2014—2015赛季部分球队的数据．

表3　2014—2015赛季部分初始数据(共16行)

季后赛共有4轮比赛，均是淘汰赛制，季后赛第1轮东西部各有4轮系列赛，胜出球队可进入季后赛第2轮，而季后赛第2轮东西部各有2轮系列赛，胜出球队进入东西部决赛，一共有2轮系列赛，胜出球队最终进行NBA总决赛系列赛，即每个NBA季后赛共需进行15轮系列赛．本研究需要预测每一轮系列赛的胜负，因此需将初始数据组织成系列赛的数据形式，并加上胜负标签以便利用SVM训练模型．

本研究将系列赛对阵2支球队各项初始数据相减，从而形成系列赛数据．为保证一致性，约定由对阵双方中有主场优势一方的各项数据(除去wh， la及n)减去主场劣势球队一方的相应各项数据，再加上主场优势变量home_ad形成新的系列赛数据．对于季后赛对阵两支球队，常规赛胜场数更高的球队有4个主场，对手有3个主场，因此根据式(5)可计得home_ad的值为

home_ad=4(wh_1+la2)-3(wh_2+la_1)

(5)

其中， wh_1和la_1表示主场优势球队的wh和la； wh_2和 la_2表示无主场优势球队的wh和la． 最后加上该场系列赛的胜负标签，约定1表示主场优势一方获胜，0表示主场劣势一方获胜．表4部分地展示了2014—2015赛季最终形成的数据．其中，Δn、 Δteam_score、 Δplayer_score、Δc1、Δc2、Δc3和Δc4为本赛季与上一赛季的增量．

表4　2014—2015赛季部分最终数据(共15行)

2数据的平衡化

2.1欠采样和过采样

根据数据构成，最终形成195(13个赛季，每个赛季15轮系列赛)组系列赛数据．预测NBA季后赛胜负问题就转化为分类问题(即胜和负两类，分别用1和0表示)．但在这195组数据中胜负标签为1的样本有146个，标签为0的样本有49个，此时样本为不平衡样本．因为0类样本对于分类器提供的信息匮乏将导致训练后的模型分类不准确．在实际NBA比赛中，少数类样本点代表的是弱队在系列赛中战胜强队．这类比赛往往给观众带来不一般的刺激，因此博彩公司和球迷都希望出现大冷门．所以少数类样本在大多数情况下显得更为重要．本研究采用数据层面处理来实现平衡化，方法包括数据的欠采样和过采样．

欠采样算法是通过删减原样本数据中多数类样本的数目从而平衡样本．本研究采用逐级优化递减欠采样算法(optimization of decreasing reduction, ODR)，该算法是在k最近邻(k-nearest neighbor，kNN)分类算法的基础上利用多数类样本对零域内其他样本点的影响从而对传统欠采样算法进行改进[9-10]．设训练样本集为T， 其中多数类样本集为N， 对于N集中的任一样本p， 本研究定义所有在N集中的并且其k最近邻中含有p的样本集称为关联集，例如，关联集R={r1,r2,…,rn}， 其中样本p是ri(ri∈R)的k最近邻．ODR算法的流程如图1．

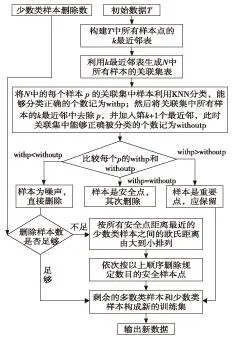
图1　ODR方法流程图Fig.1　Flow chart of ODR method

过采样算法是通过内插或复制的方式增加样本中少数类样本的数目，从而使训练样本达到平衡．传统的过采样算法一般采用的随机复制方法，偶然性过大，容易产生过拟合．一些学者提出了人工合成的过采样方法，即利用算法根据某种规则产生新的少数类样本，少数类样本合成过采样技术 (synthetic minority oversampling technique, SMOTE)是其中经典的过采样方法[12]，但这种方法并没有考虑少数类样本和多数类样本的分布特性，只是盲目的在少数类样本之间找差值，所以有学者提出边界少数类样本合成过采样技术(border synthetic minority oversample technique, BSMOTE)[8]．

算法根据少数类样本的分布情况分为噪声样本、边界样本以及安全样本．由于SVM只对边界样本敏感，所以BSMOTE只在少数类样本中的边界样本中插入新合成的样本来实现样本平衡．设训练样本集为T， 少数类样本为L={l1,l2,…,ln}． BSMOTE算法的流程如图2．

图2　BSMOTE方法流程图Fig.2　Flow chart of BSMOTE method

2.2评估指标

传统分类器的评估指标是从整体分类情况考虑的，采用所有样本的分类准确率．但在不平衡数据分类问题中，少数类样本占总样本的比重很小，错分对整体准确率的影响不大．例如有100个样本，其中A类样本99个，B类样本1个，如果分类器将所有样本都分为A类，准确率达99%，看起来性能相当不错，但是B类样本的错分率为100%．所以这并不适合评估不平衡数据的分类问题．针对传统评估指标处理不平衡样本时存在的缺陷，很多学者常常使用几何平均正确率G-mean和少数类的F-measure作为性能指标.

G-mean=

(6)

F-measure=

(7)

定义少数类样本数目为L， 多数类样本数目为N． 设FL为将多数类样本错分为少数类的样本的数目，TL为分类正确的少数类样本数目，FN为将少数类样本错分为多数类的样本数目，TN为分类正确的多数类样本数目.

从式(6)和式(7)可知，G-mean综合考虑了多数类和少数类两类样本的分类性能，要使G-mean值大，必须同时保证少数类样本的正确率和多数类样本的正确．因此若分类器只偏向于一类样本的分类性能，则G-mean值肯定很小．而F-measure也综合考虑了多数类样本和少数类样本的正确率，但侧重于体现少数类样本的分类效果[8]．本研究主要以G-mean值来评价分类器的性能．

3模型的建立

3.1训练样本和测试样本

2.1节中生成了195组系列赛的数据(这里使用因子分析数据)．取2003—2014赛季共12个赛季180组数据作为训练样本训练模型，并使用该模型预测下一赛季季后赛各系列赛比赛结果．取2014—2015赛季15个系列赛数据作为测试样本．本研究使用的是对不平衡数据较为敏感的SVM作为预测模型，这里对训练数据采用BSMOTE算法和ODR算法进行平衡化．为了确定具体的少数类样本删除数和多数类样本增加数，设置一个平衡参数β表示需要删除的多数类样本数目和多数类与少数类样本数目差值的比，用Nnum表示多数类样本的数目，Lnum表示少数类样本的数目，根据式(8)和式(9)确定样本需删增的数目分别为

deletenum=⎣(Nnum-Lnum)·β」

(8)

enlargenum=⎣Nnum-deletenum-Lnum」

(9)

这样可以保证经过处理后的训练样本中多数类和少数类样本数目相差不大．β的取值反映了算法对于数据均衡化的程度，随着均衡化的程度不同，分类器的分类性能也不同．β取值应在(0, 0.5)最佳，如果超过0.5，根据式(7)和式(8)可知，多数类样本将被删除过多导致训练样本均衡化后总数变少不利于训练模型．

3.2SVM的核函数选择

通常核函数的选择非常灵活，且已被证明凡是符合Mercer定理的函数都可作为核函数[11]．选择不同的核函数，可以生成不同的SVM，常用的核函数有：线性核函数、多项式核函数、径向基函数以及sigmoid函数．本研究通过实验选择核函数，具体的核函数选择主要根据SVM分类器对测试样本的分类的效果来判断．

3.3SVM参数的选择

在SVM的训练过程中，有一种交叉验证的方法，把训练集分成N份，每次把其中一份当做是测试集，同时用剩余几份训练分类模型，并迭代这个过程[13]．最后求出测试集分类效果最好时的参数c和g． 本研究将训练样本分为3份进行交叉验证，参数c和g的变化区间为[2-8, 28]，每次迭代后指数部加1．

3.4模型具体建立过程

训练模型建立的步骤如图3．设β=0.34，SVM核函数取RBF，惩罚参赛交叉验证结果为c=1，g=16． 以1表示结果为胜，0表示结果为负，2014—2015赛季的预测结果见表5．其中，G-mean值为0.679．

图3　模型建立过程Fig.3　Model Building

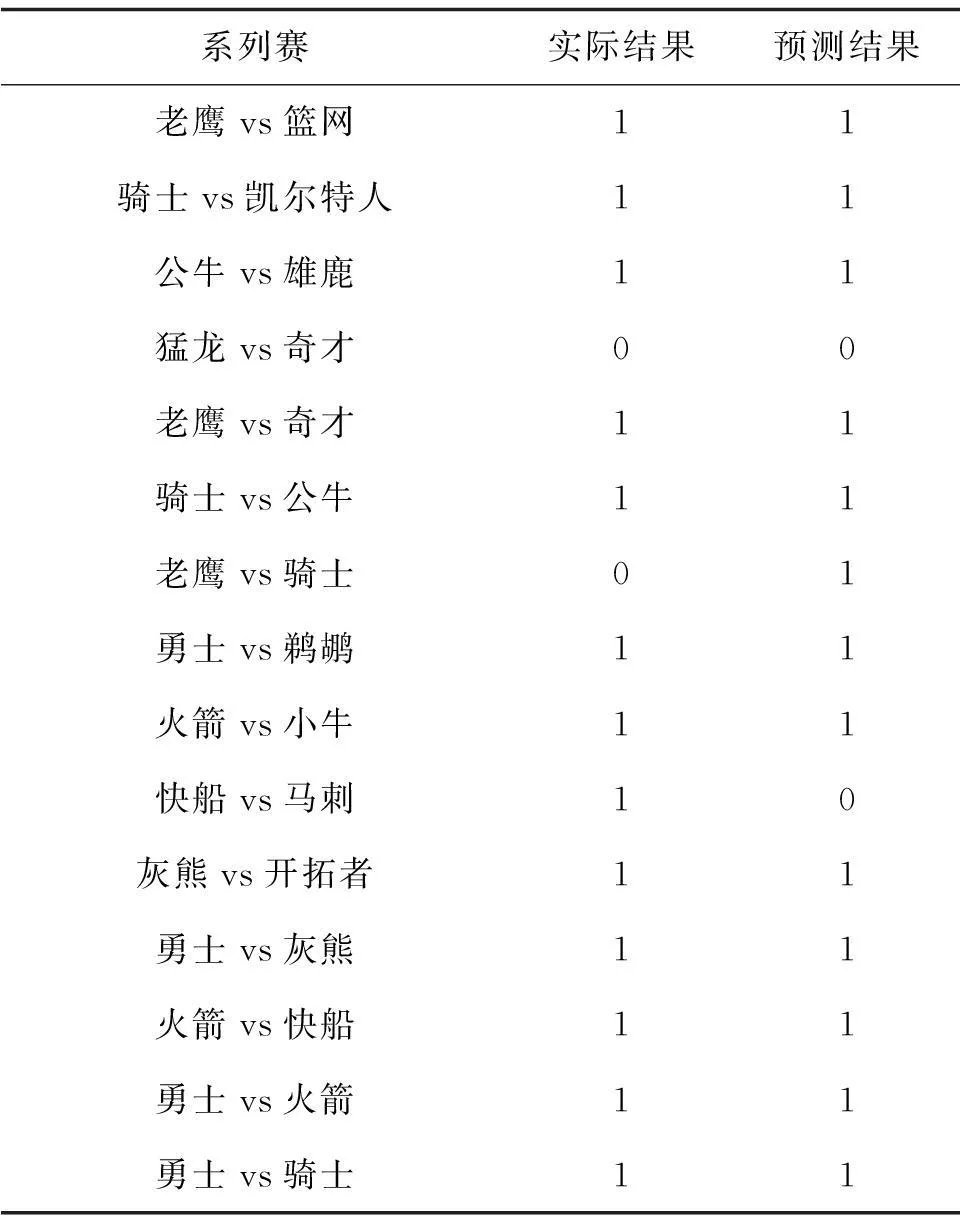
系列赛实际结果预测结果老鹰vs篮网11骑士vs凯尔特人11公牛vs雄鹿11猛龙vs奇才00老鹰vs奇才11骑士vs公牛11老鹰vs骑士01勇士vs鹈鹕11火箭vs小牛11快船vs马刺10灰熊vs开拓者11勇士vs灰熊11火箭vs快船11勇士vs火箭11勇士vs骑士11

4不同β值下的预测性能

由于平衡参数β的取值对于分类器的性能影响很大，本研究从195组数据中随机取55个数据作为测试样本，余下的作为训练样本，分别用Oliver数据、PCA数据以及因子分析数据所生成的训练样本在β值属于[0, 0.5]区间下计算分类器相应的accuracy、 G-mean及F-measure的值(由于耗时过长且效果不佳，这里不用多项式核函数)．主要参考G-mean的值，实验结果如图4．

图4中每个小图的横坐标表示β的取值，纵坐标表示相应模型的分类性能．很明显β的取值对于分类器的分类性能影响较大．本部分旨在寻找最佳核函数以及使相应分类器的G-mean值达到最高的β值．表6为3种不同数据建立SVM模型预测性能最高时的G-mean值和β值．

表6　不同数据训练SVM的最高分类性能

根据观察发现，虽然预测性能随β值变化展现出一定的混沌性，但因子分析数据较Oliver数据和PCA数据更适合训练高性能的SVM分类器；虽然RBF核函数在各数据下训练的SVM分类器有较高的accuracy值，但其对少数类样本分类的性能确实最差，因此线性核函数或者sigmoid核函数性能较之RBF会更好．因此在使用此模型预测NBA季后赛比赛结果时，可以使用因子分析构造数据，同时平衡参数β的取值在(0.04, 0.10)内，SVM核函数选择sigmoid．

体现平衡化给性能带来的提升，这里给出了使用上述因子分析数据在不经过均衡化处理下直接训练SVM后测试的结果．表7展示了6种SVM模型的测试结果．训练样本数量均为140，都是随机从195组样本中抽取的，剩余样本作为测试数据，模型SVM*表示对训练样本进行了均衡化处理，模型SVM则没有进行平衡化．不平衡比例1表示训练样本中多数类样本与少数类样本的比，不平衡比例2表示经过平衡化处理后的比例．可见经平衡化处理后的SVM模型性能明显高于未经平衡化处理的，同时核函数为sigmoid，β=0.065时达到最佳．

图4　不同数据和不同核函数在不同β值下训练SVM分类器结果图Fig.4　SVM classification results under different data, different kernel functions and diverse β

模型不平衡比例1核函数β不平衡比例2accuracyF-measure值G-mean值SVM*101∶39linear0.17591∶750.8000.6200.807SVM*101∶39RBF0.35072∶800.7090.4670.680SVM*101∶39sigmoid0.06589∶770.8360.6670.829SVM104∶36linearnull104∶360.74500SVM107∶33RBFnull107∶330.7090.2000.338SVM106∶34sigmoidnull106∶340.7450.4170.537

结语

NBA季后赛赛场较量的是每支球队的综合实力，而每支球队的综合实力都体现在漫长的82场常规赛中，如何从常规赛数据中提取真实反映球队综合实力的特征就成为预测NBA季后赛比赛胜负的关键．而预测比赛胜负的问题其实是对未知类数据的分类问题．

本研究综合分析了每支NBA球队的综合实力构成，提出球队综合实力由球队常规赛综合得分、球队核心球员综合得分、主教练水平以及主客场因素4部分数据组成．并将预测比赛结果问题转化为二分类问题用于SVM分类器上．同时对球队综合实力的评估提出了3种数据组织方式，分别是Oliver数据，PCA数据及因子分析数据．通过引入平衡参数β， 结合了欠采样算法ODR及过采样算法BSMOTE对训练数据进行预处理，消除了训练数据不平衡的现象．通过在不同的核函数下不断改变β的取值来获取分类器最佳的性能．最终得出在因子分析数据下使用sigmoid核函数并设置β值在(0.055, 0.075)之间可获得不错的分类效果．实验结果表明，经过平衡化处理后的数据可以训练一个性能更优的SVM分类器．

本研究在分析NBA球队综合实力时并未考虑球员在季后赛时期的伤病影响以及球队阵容的化学反应，同时球员评价公式并不能完全反映一个超级球星的全部实力．因此进一步的研究应该是如何更加准确地从常规赛数据中提取更多的影响球队季后赛胜负的信息．

引文：曾磐，朱安民．基于支持向量机的NBA季后赛预测方法[J]. 深圳大学学报理工版，2016，33(1)：62-71.

参考文献/ References：

[1] Melnick M J. Relation between team assists and win-loss record in the National Basketball Association[J]. Percept Mot Skills，2001, 92(2): 595-602.

[2] 靳勇．2005—2006赛季NBA总决赛制胜因素探析[J]．哈尔滨体育学院学报，2006，24(6)：118-119．

Jin Yong. The winning factors of the finals of 2005—2006 NBA season[J]. Harbin Sports Institute Proceedings, 2006, 24(6): 118-602.(in Chinese)

[3] 邱胜，段重阳，陈征．NBA季后赛成绩分析及预测：Logistic和Bayes模型[J]．统计教育，2010(10)：46-51．

Qiu Sheng, Duan Chongyang, Chen Zheng. Analysis and forecast of playoff teams promotions with Logistic and Bayes model[J]. Statistical Education, 2010(10): 46-51.(in Chinese)

[4] Chatterjee S, Campbell M R, Wiseman F. Take that Jam! An analysis of winning percentage for NBA teams[J]. Managerial and Decision Economics, 1994, 15(5): 521-535.

[5] Ni Jianjun, Zhang Chuanbiao, Ren Li, et al. Abrupt event monitoring for water environment system based on KPCA and SVM[J]. IEEE Transactions on Instrumentation and Measurement, 2012, 61(4): 980-989.

[6] Torheim T, Malinen E, Kvaal K, et al. Classification of dynamic contrast enhanced MR images of cervical cancers using texture analysis and support vector machines[J]. IEEE Transactions on Medical Imaging, 2014, 33(8): 1648-1656.

[7] Sports Reference LLC. Glossary: poss, GmSc[DB/OL].[2015-09-11]. http://www.basketball-reference.com/about/glossary.html.

[8] 童智靖．不均衡数据下基于SVM的分类算法研究与应用[D]．哈尔滨：哈尔滨工程大学，2011．

Tong Zhijing. Unbalanced data classification algorithm based on SVM for research and application[D]. Harbin: Harbin Engineering University, 2011.(in Chinese)

[9] Bhanu P K N, Ramakrisbnan A G, Suresh S, et al. Fetal lung maturity analysis using ultrasound image features[C]// IEEE Transactions on Information Technology in Biomedicine.[S.l.]:IEEE, 2002, 6(1): 38-45.

[10] Alpaydin E．机器学习导论[M]．2版．范明，昝红英，牛常勇，译．北京: 机械工业出版社，2009：1-2，142．

Alpaydin E. Introduction to machine learning[M]. 2nd ed. Fan Ming, Zan Hongying, Niu Changyong, trans. Beijing: China Machine Press, 2009: 1-2, 142.(in Chinese)

[11] Wang F, He K, Liu Y, et al. Research on the selection of kernel function in SVM based facial expression recognition[C]// The 8th IEEE Conference on Industrial Electronics and Applications (ICIEA). Melbourne, Australia: IEEE, 2013: 1404-1408.

[12] Chawla N V, Bowyer K W, Hall L O, et al. SMOTE: synthetic minority over-sampling technique[J]. Journal of Artificial Intelligence Research, 2002, 16(1): 321-357.

[13] Zhu Anmin, Yi Xin. The comparisons of four methods for financial forecast[C]// Proceeding of the IEEE International Conference on Automation and Logistics. Zhengzhou: IEEE, 2012: 45-50.

【中文责编：英子；英文责编：雨辰】

Received：2015-05-01；Accepted：2015-12-07

Foundation：National Natural Science Foundation of China (61300192)；National Key Technology Support Program of China (2013BAH33F00)；Research Foundation of NARI Group Corporation(SGTYHT/14-XX-194)

† Corresponding author：Engineer Zhang Zonghua．E-mail: Zhangzonghua@sgepri.sgcc.com.cn

Citation：Zhang Zonghua,Zhang Haiquan,Li Shihang,et al．Disk usage prediction based on an improved weighted moving average method[J]. Journal of Shenzhen University Science and Engineering, 2016, 33(1): 72-79.(in Chinese)

【电子与信息科学 / Electronics and Information Science】

A SVM-based model for NBA playoffs prediction

Zeng Pan and Zhu Anmin†

College of Computer Science and Software Engineering, Shenzhen University, Shenzhen 518060,

Guangdong Province, P.R.China

Abstract：We use four statistics data from the NBA regular season including team comprehensive score, player comprehensive score, chief coach capability, and the impact of home and away games as the indicators to build up training samples. Then, we construct a prediction model based on a support vector machine (SVM), which is suitable for solving the problem of a small sample size and has the theoretical basis of structural risk minimization. We combine the technique of undersampling and oversampling to remove the unbalanced data in training datasets, thus improving the leaning ability of SVM. Experimental results show that the proposed method has a relatively preferable performance.

Key words：computer perception; NBA playoffs; factor analysis; support vector machine; unbalanced data; undersampling; oversampling

作者简介：曾磐(1992—)，男，深圳大学硕士研究生．研究方向：数据挖掘．E-mail：q64545@sina.com

基金项目：国家自然科学基金资助项目(61273354)

中图分类号：TP 391

文献标志码：A

doi：10.3724/SP.J.1249.2016.01062