一种改进的即时解码网络编码的无线重传策略
肖 巍,梅中辉
(南京邮电大学 通信与信息工程学院,江苏 南京 210003)
一种改进的即时解码网络编码的无线重传策略
肖 巍,梅中辉
(南京邮电大学 通信与信息工程学院,江苏 南京 210003)
为了充分利用网络编码的优势,文中提出一种改进的基于即时解码网络编码的无线重传策略。该策略从图论(编码机会)的角度出发,为了减少编码数据包的重传次数,在考虑剩余编码机会和剩余数据包需求的条件下选择编码数据包,使每一步选择的重传编码数据包组合能够保证剩余编码密度(实际编码机会和最大编码机会之比)最大,并且针对同等编码密度的情况,进一步考虑平均解码时延最小者为所选择的网络编码重传方式。研究表明,所提出的策略相对于服务最大需求数据包策略和随机编码子集选择策略,能够进一步减少重传次数,降低平均解码时延。
网络编码;重传策略;解码时延;编码密度
0 引 言
在无线广播信道中,网络编码[1]能够显著提高吞吐量和传输效率,吞吐量和传输效率的优化是目前的研究热点之一[2-9]。针对在无线网络中由于存在删除信道(Erasure Channel)而导致信宿节点不能成功收到所有的数据包的问题,已有人提出利用随机线性网络编码[10]去解决,但在随机线性网络编码模型下,信宿节点需要收到足够多的数据包才能进行解码,因此这种模型下的解码时延非常大。为了确保无线传输的可靠性,同时尽量提高传输效率,一种基于反馈矩阵的即时解码网络编码(Instantly Decodable Network Coding,IDNC)[11]方案被提出。
为了优化某一给定的性能指标,大部分的基于IDNC的数据包重传策略只考虑每次传输解码出的需求数,并未考虑重传的编码数据包组合对剩余编码机会的影响。然而随着编码机会的减少,从中获取的网络编码增益就会减少。基于这一点,文献[12]通过缓存未即时解码的数据包来达到增加编码机会的目的。由于文献[12]中的方法并不适用于IDNC,Sorour S等提出一种基于IDNC的服务最大需求数据包策略(Most Wanted Packet Serving Strategy,MoWPS)[13]。该策略与随机编码子集选择策略(Random clique selection,RND)[3]相比,能够减少重传次数;但是在出现同等编码密度的情况下并没有考虑选取哪种编码数据包组合进行重传。
基于上述原因,文中提出一种改进的基于即时解码网络编码的无线重传策略(Improved Retransmission Strategy based on Instantly Decodable Network Coding,IRS-IDNC)。IRS-IDNC每次选取的编码数据包组合能够最大化剩余编码密度,并且在某一次出现多个同等剩余编码密度的情况下,以最小化平均解码时延为优化目标去选取最优编码数据包组合。
1 系统模型
1.1 无线广播传输模型
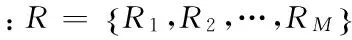
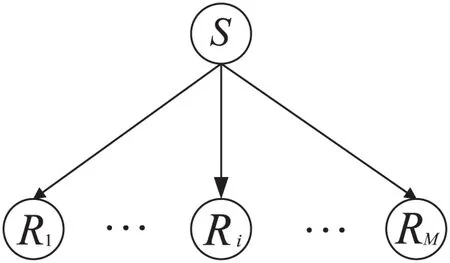
图1 无线广播传输模型
在上述广播模型中,信源节点S首先用N个时隙依次将N个原始数据包广播给M个信宿节点,此阶段称为系统传输阶段。由于无线网络下的信道衰落,并不能确保每个信宿节点都能全部接收到所有的原始数据包。在信源节点S将所有原始数据包广播传输之后,信宿节点会将自身所接收到的原始数据包信息反馈给信源节点。
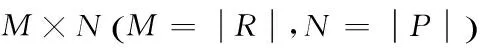
(1)
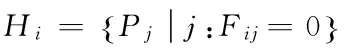
在经历了系统传输阶段之后,接下来是编码重传阶段。得到反馈矩阵F,图2为一反馈矩阵示例,其中M=5,N=6。
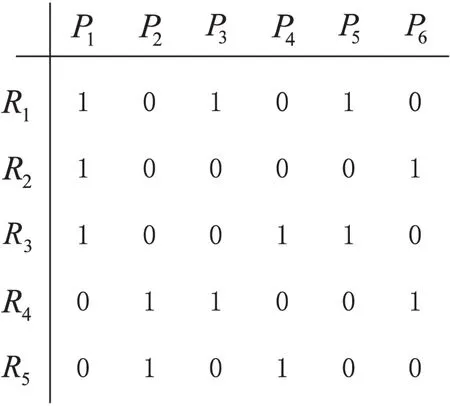
图2 反馈矩阵F
(1)j=l,说明i节点和k节点需要同一个数据包,如F中的V11和V21;
(2)j∈Hk,l∈Hi,说明i节点想要的数据包在k节点已接收的数据包集合中,并且k节点想要的数据包在i节点已接收的数据包集合中,如F中的V11和V42。
定义1(最大编码子集C):如果某一个编码数据包组合满足IDNC编码约束条件,并且再加入任何一个数据包到该编码组合都会导致信宿节点不能即时解码,那么把这样的编码数据包组合称为一个最大编码子集。
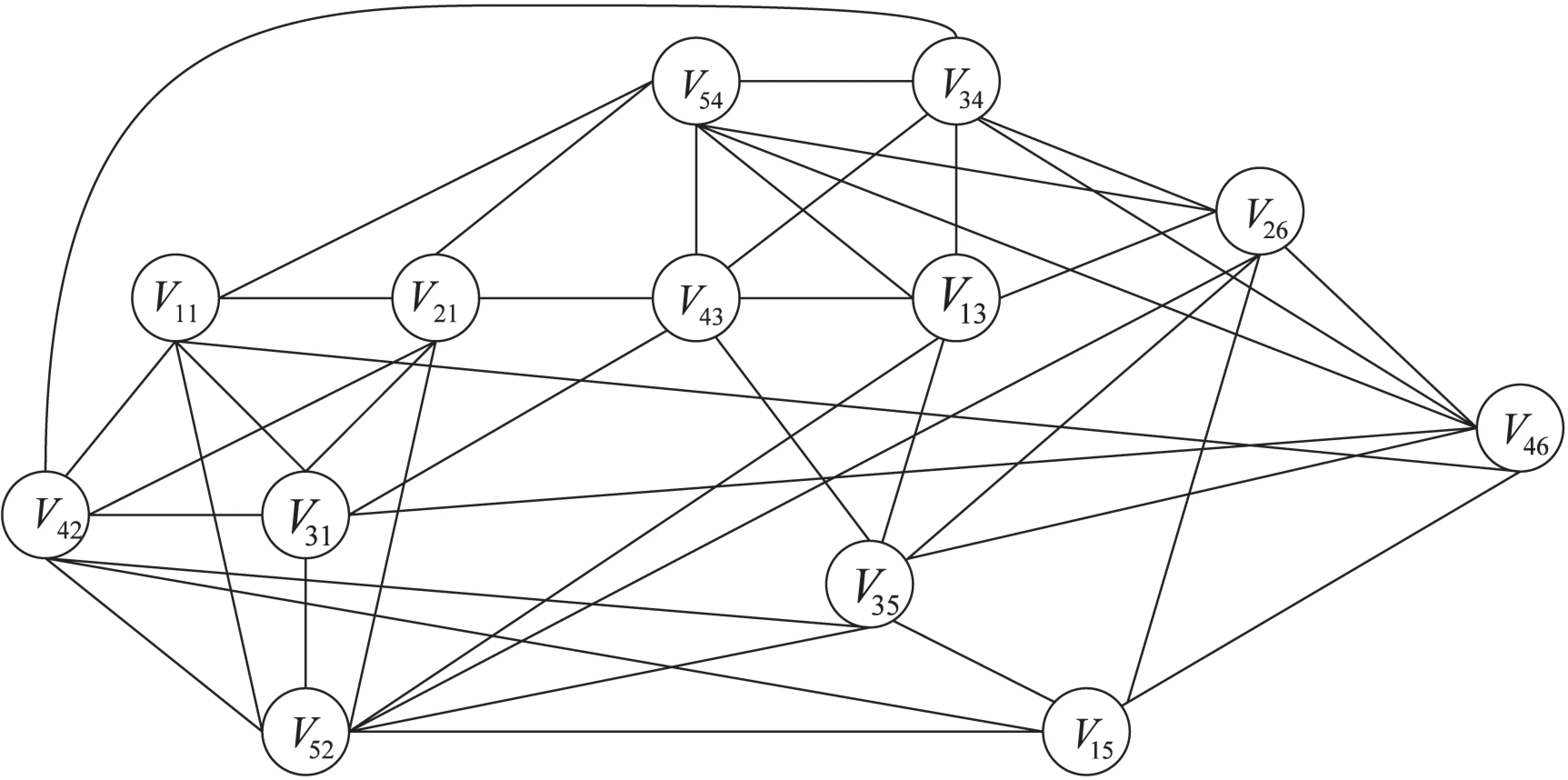
图3 IDNC无向图
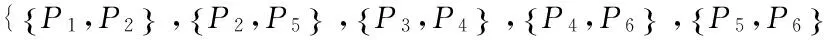
1.2 IDNC图论思想
众所周知,网络编码不仅能够显著提高传输效率和吞吐量,而且可以减少时延。很显然,应该尽可能利用每一个编码机会。
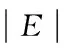
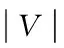
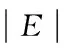
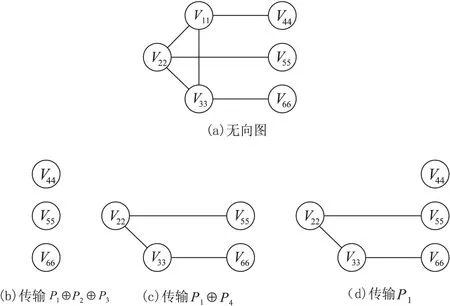
图4 编码数据包传输方式示例
从图4(b)和(c)可以看出,为了充分利用网络编码的优势,选择编码数据包组合不仅要考虑单次传输解决的需求数目,还要考虑剩余的编码机会数目。从(c)和(d)可以看出,在剩余编码机会数相同的情况下,应选择剩余顶点(需求)少的编码数据包组合以减少传输次数。
2 IRS-IDNC编码方案
2.1 IRS-IDNC思想与分析
根据1.2节的描述可知,为了充分利用网络编码机会,同时减少传输次数,选择的编码数据包组合应使剩余的编码机会越大越好,同时使剩余的顶点数越少越好(此时剩余的最大编码机会也相应变少)。也就是说,在传输完选取的编码数据包组合之后,剩余的编码密度应该越大越好。
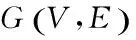
(2)
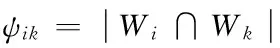
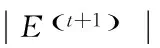
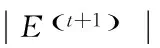
(3)
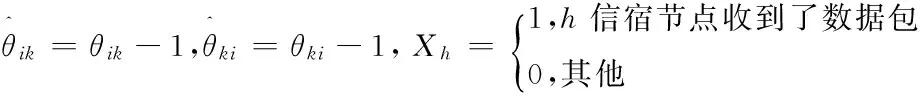
引理3:系统平均解码时延[15]为:
(4)
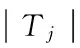
2.2 IRS-IDNC方案
为了能够充分利用网络编码机会并且降低系统平均解码时延,文中提出的IRS-IDNC方法如下:
(1)根据某一时刻得到的反馈矩阵,利用Bron-Kerbosch算法[16]找出该反馈矩阵对应的所有最大编码子集;
(2)选择某一个最大编码子集C(称为最优编码子集)进行传输,确保该最大编码子集能够包含尽量多的同求数据包,并且解码尽量多的需求,也就是使式(5)的目标函数最大[13]:
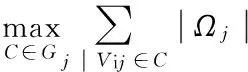
(5)
其中,Ωj是需要数据包j的信宿节点数目。
如果在通过Bron-Kerbosch算法得到的最大编码子集中,有两个或多个最优编码子集,那么将保留该组最优编码子集,并假定系统分别选择这些最优编码子集进行传输。后续每一次出现多个最优编码子集时,都按照此策略选择编码数据包直到反馈矩阵F更新全零矩阵。
(3)依次记录由上述策略所得到的最大编码子集传输序列。
(4)根据式(4),分别计算每一个记录下的最大编码子集传输序列对应的平均解码时延,并最终选取平均解码时延最小的最大编码子集序列进行重传。
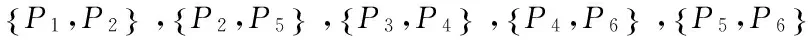
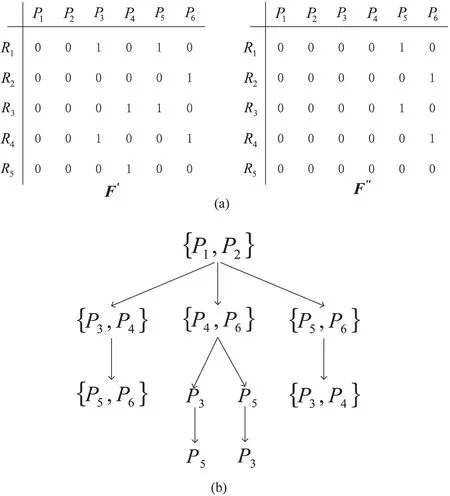
图5 反馈矩阵和最大编码子集树图
3 仿真结果及分析
为了验证IRS-IDNC方案的有效性,文中使用MATLAB对图1中的无线广播信道传输模型进行仿真。主要对RND方案、MoWPS方案和文中提出的IRS-IDNC方案的平均传输次数和系统平均解码时延进行仿真,并且对三者进行性能比较和分析。
首先,为确保能够观察性能指标在不同信宿节点M下的变化趋势,设定每个信宿节点的丢包率Pe=0.2,原始数据包N=15,信宿节点M在5到30之间变化,并选取200个样本数进行仿真,仿真结果如图6(a)所示。
同样,设定每个信宿节点的丢包率Pe=0.2,信宿节点个数M=15,数据包个数N在5到30之间变化,并选取200个样本数进行仿真,仿真结果如图6(b)所示。
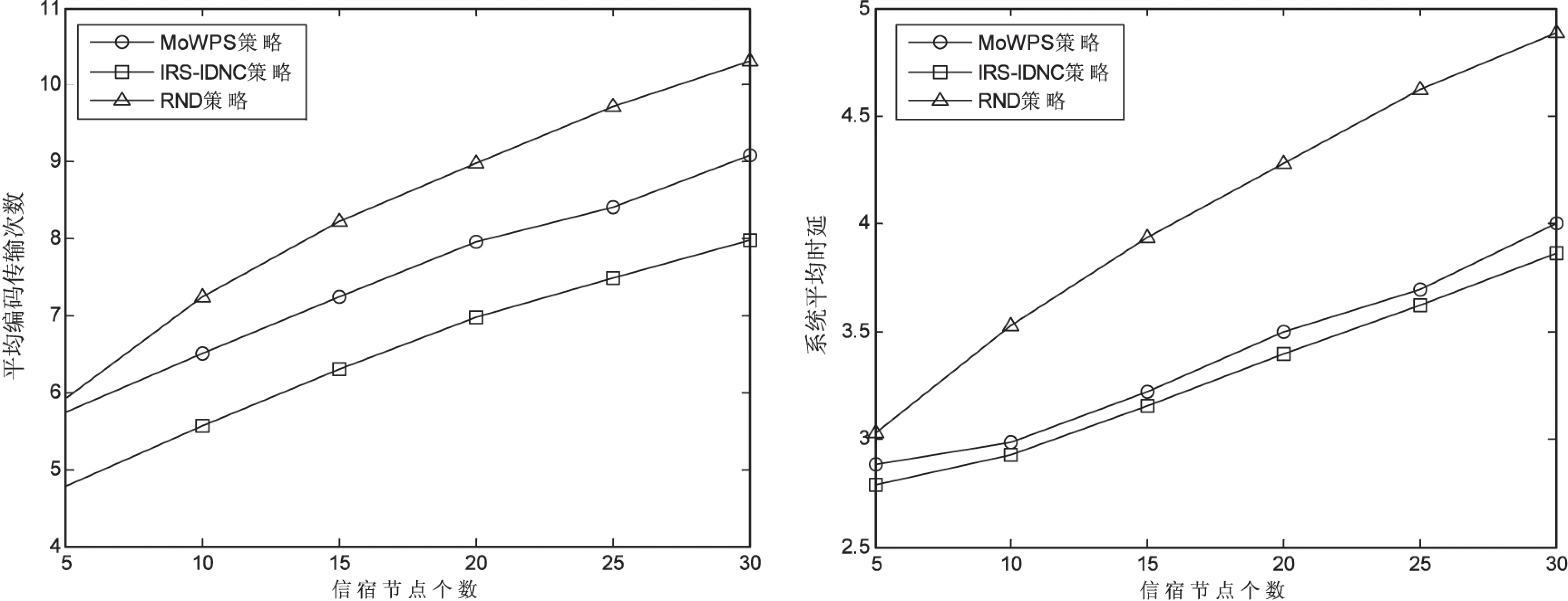
(a)不同信宿节点时的系统性能
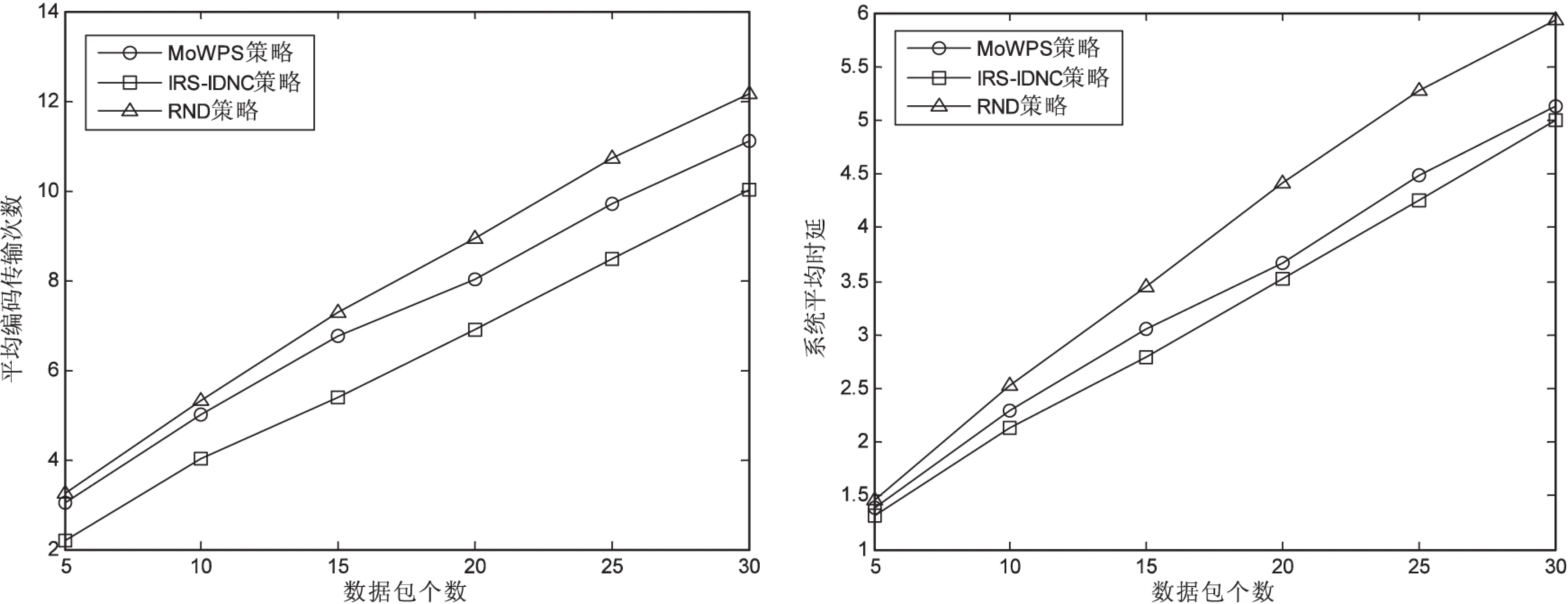
(b)不同数据包数目时的系统性能
从图6中可以看出,三种方案的传输次数和平均解码时延都随着信宿节点或数据包个数增加而增加。其中,IRS-IDNC方案的传输次数和平均解码时延优于RND方案和MoWPS方案。这是因为RND方案在选择最大编码子集时是进行随机选取的,而没有考虑剩余的编码机会,MoWPS方案的最大编码子集选择虽然考虑了剩余编码机会,但是没有进一步考虑当多个最大编码子集的剩余编码密度相同时,如何使系统平均解码时延最小;而IRS-IDNC方案既充分利用了编码机会,而且当出现多个最大编码子集而导致编码密度相同的情况时,以最小化系统平均解码时延为目标去选取最大编码子集,从而可相应降低系统平均解码时延。
4 结束语
文中主要借助图论思想从编码机会的角度对基于IDNC的无线广播重传问题进行了研究。为了充分利用网络编码的优势,针对MoWPS策略没有考虑如何处理出现多个最大编码子集对应的剩余编码密度相同的情况,文中结合编码密度和平均解码时延,提出了IRS-IDNC方案。仿真结果与分析表明,与RND方案和MoWPS方案相比,IRS-IDNC能够有效减少重传次数,降低系统平均解码时延。
[1] Ahlswede R,Cai N,Li S Y R,et al.Network information flow[J].IEEE Transactions on Information Theory,2000,46(4):1204-1216.
[2] Sundararajan J K,Shah D,Medard M.Online network coding for optimal throughput and delay-the three-receiver case[C]//Proc of international symposium on information theory and its applications.[s.l.]:IEEE,2008.
[3] Keller L,Drinea E,Fragouli C,et al.Online broadcasting with network coding[C]//Proc of fourth workshop on network coding theory & applications.Hong Kong:[s.n.],2008.
[4] Drinea E,Fragouli C,Keller L.Delay with network coding and feedback[C]//Proceedings of ISIT.[s.l.]:[s.n.],2009:844-848.
[5] Rouayheb S E,Chaudhry M A R,Sprintson A,et al.On the minimum number of transmissions in single-hop wireless coding networks[C]//Proc of information theory workshop.[s.
l.]:IEEE,2007:120-125.
[6] Dong N,Nguyen T,Xue Y.Multimedia wireless transmission with network coding[C]//Packet video 2007.Lausanne,Switzerland:IEEE,2007:326-335.
[7] Seferoglu H,Markopoulou A.Video-aware opportunistic network coding over wireless networks[J].IEEE Journal on Selected Areas in Communications,2009,27(5):713-728.
[8] Seferoglu H,Markopoulou A.Opportunistic network coding for video streaming over wireless[C]//Packet video 2007.Lausanne,Switzerland:IEEE,2007:191-200.
[9] Sundararajan J K,Sadeghi P,Médard M.A feedback-based adaptive broadcast coding scheme for reducing in-order delivery delay[C]//Proc of IEEE workshop on network coding,theory and application.Lausanne:IEEE,2009:1-6.
[10] Ho T,Medard M,Koetter R,et al.A random linear network coding approach to multicast[J].IEEE Transactions on Information Theory,2006,52(10):4413-4430.
[11] Sadeghi P,Shams R,Traskov D.An optimal adaptive network coding scheme for minimizing decoding delay in broadcast erasure channels[J].EURASIP Journal on Wireless Communications & Networking,2010,2010:50-50.
[12] Wang C C.On the capacity of 1-to-K broadcast packet erasure channels with channel output feedback[J].IEEE Transactions on Information Theory,2010,58(2):1347-1354.
[13] Sorour S,Valaee S.Coding opportunity densification strategies for instantly decodable network coding[J].IEEE Transactions on Communications,2013,61:5077-5089.
[14] Harris J M,Hirst J L,Mossinghoff M J.Combinatorics and graph theory[M]//Undergraduate texts in mathematics.Berlin:Springer,2008.
[15] Yu M,Sadeghi P,Aboutorab N.On the throughput and decoding delay performance of instantly decodable network coding[J].IEEE/ACM Trans on Networking,2013,67:1309-1310.
[16] Bron C,Kerbosch J.Algorithm 457:finding all cliques of an undirected graph[J].Communication of the ACM,1973,16(9):575-577.
An Improved Wireless Retransmission Strategy Based on Instantly Decodable Network Coding
XIAO Wei,MEI Zhong-hui
(College of Telecommunication & Information Engineering,Nanjing University of Posts and Telecommunications,Nanjing 210003,China)
To take full advantage of the advantages of network coding,an improved wireless retransmission strategy based on instantly decodable network coding is proposed in this paper.This strategy is researched with graph theory.In order to reduce the numbers of broadcast retransmissions,when doing the selection of a coding combination,the remaining coding opportunity and remaining packet requests are considered.So each coding packet of selection can maximize the remaining coding density (the ratio of the number of actual coding opportunities to the maximum number of coding opportunities).If the number of optimal selection is large with the same coding density,the retransmissions will be chosen to minimize the average decoding delay.Research illustrates that the strategy proposed in this paper is possible to reduce the numbers of retransmissions and average decoding delay compared with most wanted packet serving strategy and random clique selection strategy.
network coding;retransmission strategy;decoding delay;coding density
2015-06-13
2015-09-18
时间:2016-02-18
国家科技重大专项(2010zx03003-003)
肖 巍(1990-),男,硕士研究生,研究方向为网络编码技术、资源优化等;梅中辉,副教授,硕士研究生导师,研究方向为网络编码技术、协助通信技术等。
http://www.cnki.net/kcms/detail/61.1450.TP.20160218.1634.044.html
TP301
A
1673-629X(2016)03-0144-05
10.3969/j.issn.1673-629X.2016.03.034

