求解车辆路径问题的改进MMAS算法
谢骊玲,宋彦斌,杨 坦,骆其伦
(华南师范大学 数学科学学院,广东 广州 510631)
求解车辆路径问题的改进MMAS算法
谢骊玲,宋彦斌,杨 坦,骆其伦
(华南师范大学 数学科学学院,广东 广州 510631)
最大-最小蚂蚁系统(MMAS)只在最优解对应的路径上更新信息素,有效地利用了最优解,但容易导致搜索过早停滞。文中分析了MMAS在求解车辆路径问题(VRP)时的表现,针对其容易陷入局部最优解、全局搜索能力差、后期收敛速度慢等不足提出改进,给出一种新的信息素更新策略,动态改变挥发系数的数值,并在较优的几条路线上进行信息素更新,从而在加速算法收敛的同时提高全局搜索能力,避免过早停滞。VRP仿真实验结果表明,改进后的算法稳定性好,收敛速度比原始MMAS算法有明显的提高。
车辆路径问题;优化算法;蚁群算法;最大-最小蚂蚁系统;信息素更新
1 概 述
车辆路径问题(Vehicle Routing Problem,VRP)最早是1959年由G. Dantzig等提出的,问题可描述为:在诸如容量、总路程、时间窗、送货顺序等限制条件下,找到从一个或多个初始点出发,到多个不同位置的客户的最优送货路径,即设计一个总代价最小的路线集,满足:每个客户只被一辆车访问一次且所有车辆从起点出发再回到起点[1]。例如,最简单最经典的VRP的要求是所有车辆的行驶路线使总的运输成本最小。
车辆路径问题是物流配送优化中的关键环节,也是管理科学中的一个重要研究课题。多年来运筹学、应用数学、物流科学、计算机科学等学科学者对这个问题进行了大量的理论研究和实验分析,取得了很大的进展。
VRP是一个NP难题,随着配送客户数量的增加,可选的车辆路径方案数量将以指数速度急剧增长。当问题规模较大时,利用传统的理论寻优算法难以严格获得精确最优解,因此求解该问题的主要方法是启发式算法,后者一般能够在一定时间内找到满意的近似最优解,这是前者难以达到的。目前已成功应用于VRP的启发式算法有扫描法[2]、节约法[3]、最近插入法[4]、遗传算法[5]、神经网络[6]、蚁群算法[7-8]、模拟退火法[9]、禁忌搜索法[10]等。这些方法各有优缺点,以经典TSP为测试基准,除了Lin-Kernighan的局部改进法之外,由意大利科学家Dorigo M等提出的蚁群算法(Ant Colony Algorithm)优于其他方法[1]。
蚁群算法是一种仿生类算法,应用范围几乎遍及各个领域。国内外多年的研究工作表明,蚁群算法在求解组合优化问题、离散优化问题方面都取得了成功,充分说明蚁群算法是一种非常有效的优化方法。蚁群算法自提出至今已在聚类分析、自动控制、系统工程、通信网络路由选择、车间调度问题、车辆路径问题等方面都得到了成功的应用。算法在求解过程中利用蚂蚁群体的系统性、自组织性、正反馈性和分布式计算,使算法演化过程得以进行,并且朝着优化方向收敛;另一方面,通过在算法中加入概率搜索技术来增加负反馈机制,从而提高了生成解的随机性,一定程度上保持了解的搜索范围,避免算法过早收敛于不好的结果。但是蚁群算法本身还是存在着搜索初期信息素匮乏、信息素积累时间较长、易陷入局部最优解的缺陷。所以研究者们提出了一系列的改进蚁群算法[11-15]。其中由Stützle等提出的最大-最小蚁群算法[16](Max-Min Ant Colony Algorithm,MMAS)是目前国际公认的用于解决VRP效果最好的蚁群算法[17]。
文中针对车辆路径问题的特点,提出了一种改进的MMAS算法,给出一种新的信息素更新策略,通过动态改变信息素的挥发系数,达到在提高收敛速度的同时有效地防止停滞。
2 车辆路径问题的描述
根据考虑因素的多寡、限制条件的不同,可以将车辆路径问题分成几种类型,但不管带有何种条件的约束,配送总费用总是一个需要着重考虑的问题,而路径的选择则直接影响了配送费用的高低。
为使问题的描述更接近文中要解决的问题,下面以配送中心车辆调度问题为例重述VRP:已知若干客户的位置坐标和货物需求量,配送车辆的负载能力,每辆车从已知位置的物流中心出发,完成向多个客户送货的任务后回到起点。要求合理安排车辆配送路线,使配送总费用最少,即总里程最短,且满足以下约束条件:
(1)每辆车所配送的客户的需求量总和不超过车辆的负载能力;
(2)每个客户的需求必须满足,且只由一辆车配送。
显然这是一个经典的有容量限制的车辆路径问题(CVRP),在不引起混淆的情况下,许多文献直接将CVRP简称为VRP。一般地,该问题的数学模型可以表述如下[1]:
设
则要解决的问题即为:
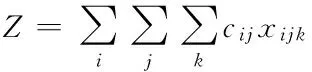

其中:约束(a)是车辆负载能力;约束(b)保证每个客户只被一辆车访问一次;约束(c)-(e)保证每辆车完成任务后回到起点。参数cij是位置i到位置j的距离;di是客户i的需求量;D为单车额定载重量。
3 MMAS算法的原理和实现步骤
3.1 算法原理
MMAS算法与基础的AS算法比较,主要作了如下改进:

(2)完成一次迭代后,只更新最优解所在路径上的信息,充分保留了历史最优解的信息;
(3)算法开始时,信息素挥发速率ρ初始值较小,以便在迭代初期能让蚂蚁搜索到更多可能的路径。但为保证搜索能顺利进行,信息素的初始值被设定为上限值τmax,使得算法能在搜索初期加大对新解的探索,不至于一开始就快速接近局部最优解。从文献实验中还可发现,在迭代过程中,逐步提高全局最优解的应用频率,可加快算法的搜索过程。
3.2 算法步骤
求解CVRP的带有局部优化步骤的MMAS算法(算法1)如下:
Step1:蚂蚁初始化。设有N个客户点,每条边上的信息素初始值为τmax,将N只蚂蚁放在配送中心所在节点上,每只蚂蚁的负载能力代表车辆的额定载重D;与实际蚁群不同,人工蚁群系统具有记忆功能,所以为每只蚂蚁建立空禁忌表tabuk(k=1,2,…,N),用以记录蚂蚁k当前所走过的城市,集合随迭代过程动态调整。
Step2:条件终止判断。当定时时间到,或达到最大迭代次数,或最优解重复达到指定次数,结束算法,转Step6;否则对蚁群中的每只蚂蚁,重复执行以下步骤。
Step3:路径构建。tabuk的补集中小于等于当前蚂蚁的负载量剩余的节点作为备选节点,即allowedk={0,1,…,N-1}-tabuk,每只蚂蚁根据如下转移概率公式选择下一个节点,逐步形成完整路线。
同时将该节点加入tabuk中,更新当前每只蚂蚁的负载量,若tabuk的补集中各节点的需求量di均大于当前剩余的负载量,则直接返回配送中心。
Step4:路径改进。采用2-Opt局部搜索方法对第3步中形成的路线进行优化。
Step5:轨迹更新。当N只蚂蚁均完成遍历任务后,找出该代次最佳路径并保留(当前迭代最优解):
lmin=minlk,k∈{1,2,…,N}
式中,lk为第k只蚂蚁走过的路程之和。
然后更新信息素,增加该次迭代中表现最好的蚂蚁经过路径上的信息素浓度,信息素浓度更新规则如下:
(1)

Step6:输出结果。
4 改进的MMAS算法步骤
由3.2的MMAS算法步骤可知,在迭代过程中需要对若干参数进行设定,参数的取值对算法性能会有一定的影响,其中信息素挥发度参数ρ的取值直接影响到算法的收敛性和全局搜索能力。信息素挥发度与信息的正反馈作用是此消彼长的关系。ρ较大,则正反馈作用较弱,算法的收敛速度慢,但搜索的随机性提高;反之则算法收敛速度较快而搜索的随机性降低,算法容易出现搜索停滞。所以对ρ的选择需要综合考虑算法的全局搜索能力和收敛速度。
基本的MMAS算法将各条路径上的信息素浓度值限定在固定的范围内,虽然能在一定程度上避免过早陷入局部最优解,但当解的分布较分散时收敛速度较慢;另外,每完成一次迭代后,没有考虑到各条可能路径的优劣情况,仅以固定的挥发系数ρ对当前最优路径上的信息素进行更新,有可能由于对当前最优路线的更新远大于其他路径,从而使某些次优、次次优的路径没有机会被选中,导致算法在这些路径上的搜索能力相对较低,造成算法的全局寻优性能变差,影响了算法的随机性能和全局搜索能力。
从上述分析过程可看出,固定挥发系数ρ的值总是有弊端,所以可通过动态地改变ρ的值来提高算法的全局搜索能力,并且同时应兼顾到次优路径的信息素更新问题。
综合文献中的实验结果,容易发现,蚁群算法在迭代到一定程度后,蚂蚁对信息素的浓度逐渐变得不敏感,各条路径上的信息素最大差距趋向于固定数值(上限值-下限值),此时算法将会出现一定程度的搜索停滞。在一定的迭代次数内所得的解大致接近,如果固定挥发系数ρ,即使每次迭代都更新信息素的量,对解也不会有太大的改进。因此为加快迭代速度,考虑在迭代过程中动态地修改挥发系数ρ的值,并修改信息素更新规则。
根据上述分析,在搜索的前期和后期,为保留最优路径更多的信息,ρ应该取得小一些,在搜索的中期,为加快迭代速度,ρ可以取得较大一些。易见ρ与迭代次数n有关,因此构造如下关于迭代次数n的函数动态地改变挥发系数ρ的值,用以路径的信息素更新过程。
(2)
其中,自变量n为迭代次数,并且在式(1)中,将更新规则修改为:
(3)
得到文中算法2。
MMAS只对最优路径上的信息素进行全局更新,即只增强最优解的影响程度。这种做法当解的分布较集中时收敛速度较快,但当解的分布较分散时容易出现局部收敛。为避免过早停滞,选择同时在最优的bn个路径上进行信息素更新,并根据路径的优劣程度相应地在这bn个路径上依次降低更新概率,具体规则修改如下:
由算法1的第5步,一次迭代完成后,根据路径长度将路径重新排序,假设由短到长依次排序为l1 其中,k=1,2,…,bn。 由此得到算法3。 最后,为保证信息素更新后依然满足MMAS关于信息素浓度的限制,达到避免停滞现象发生的目的,在信息素更新步骤(见式(2))后面加上判断条件: end 为了验证文中提出的带有动态信息素调整策略的算法2和带有改进更新规则的算法3比原始的MMAS算法具有更佳的全局最优解搜索能力和更高的收敛速度,以NEO网站中提供的VRP问题的数据(http://neo.lcc.uma.es/vrp/vrp-instances/capacitated-vrp-instances/)为例进行实验。实验的硬件环境为Intel酷睿i5-2450,内存8G;软件环境为MATLAB2013b。实验中所采用的部分参数统一取值如下:最大循环次数NCmax=3 000,蚂蚁个数m=20,重要度系数α=1,能见度系数β=2。 实验结果如表1和表2所示。 其中:最优解是已知的该问题最好的解;平均解是指运行3次所得的3个解的平均值;平均时间是指各次运行中找到最好解的时间的平均值,单位为s。 表1 算法2的实验结果对比 表2 算法3的实验结果对比 实验结果表明,带有动态信息素调整策略的算法2以及带有改进更新规则的算法3均比原始的MMAS算法的稳定性好,全局搜索能力较强,而算法效率与带局部改进的MMAS算法相当,比原始的MMAS收敛速度快。 从蚁群搜索最短路径的机制不难发现,算法中参数的选择明显地影响到蚁群算法的性能,但对各参数的选取方法和原则,通常都是根据经验而定的,尚没有理论上的依据。文中在对车辆路径问题进行简单描述的基础上,通过对MMAS算法中有关参数的讨论,发现原有算法虽然具备较好性能,但是因为算法中各参数都是固定的,没有根据求解过程动态变化,依然存在容易陷入局部最优解、全局搜索能力差、收敛速度慢等基本蚁群算法的不足。 基于上述缺陷,文中提出一种求解车辆路径问题的改进的自适应最大-最小蚂蚁算法,对MMAS算法中的一些参数及策略作了自适应变化,给出动态调整的信息素挥发系数和新的信息素更新策略,使得算法在求解问题时能在求解过程中随着解状态的变化而相应变化,从而具有更好的算法性能。实验结果表明,带有动态信息素调整策略和新的信息素更新规则的MMAS算法增强了蚂蚁搜索的有效性,提高了算法的寻优性能;而且算法效率与带局部改进(2-Opt)的MMAS算法相当,收敛速度比原始的MMAS算法有较大的提高。 文中提出的求解车辆路径问题的改进算法对解决类似的组合优化问题有一定的参考价值。但是,限于篇幅关系,没有讨论其他参数对算法有效性、稳定性和收敛性的影响,这将是接下来的一个研究方向。 [1] 马 良,朱 刚,宁爱兵.蚁群优化算法[M].北京:科学出版社,2008. [2]GillettBE,MillerLR.Aheuristicalgorithmforthevehicledispatchproblem[J].OperationsResearch,1974,22(2):340-349. [3] 方金城,张岐山.物流配送车辆路径问题(VRP)算法综述[J].沈阳工程学院学报:自然科学版,2006,2(4):357-360. [4] 赵燕伟,张景玲,王万良.物流配送的车辆路径优化方法[M].北京:科学出版社,2014. [5] Laporte G,Mercure H,Nobert Y.An exact algorithm for the asymmetrical capacitated vehicle routing problem[J].Network,1986,16:33-46. [6] 王德东,郑丕谔.车辆路径问题的混沌神经网络解法[J].计算机集成制造系统,2005,11(12):1747-1750. [7] Bullnheimer B,Hartl R F,Strauss C.An improved ant system algorithm for the vehicle routing problem[J].Annals of Operations Research,1999,89(13):319-328. [8] Dorigo M,Stützle T.Ant colony optimization:overview and recent advances[M]//International series in operations research & management science:handbook of metaheuristics.US:Springer,2010:227-263. [9] 胡大伟,朱志强,胡 勇.车辆路径问题的模拟退火算法[J].中国公路学报,2006,19(4):123-126. [10] Barbarrosoglu G,Ozgur D.A tabu search algorithm for the vehicle routing problem[J].Computers & Operations Research,1999,26(3):255-270. [11] 李 琳,刘士新,唐加福.改进的蚁群算法求解带时间窗的车辆路径问题[J].控制与决策,2010,25(9):1379-1383. [12] Chen C,Ting C.An improved ant colony system algorithm for the vehicle routing problem[J].Journal of the Chinese Institute of Industrial Engineers,2006,23(2):115-126. [13] Gan R,Guo Q,Chang H,et al.Improved ant colony optimization algorithm for the traveling salesman problems[J].Journal of Systems Engineering and Electronics,2010,21(2):329-333. [14] 刘晓勇,付 辉.基于启发式蚁群算法的VRP问题研究[J].计算机工程与应用,2011,47(32):246-248. [15] 张 锦,李 伟,费 腾.交叉变异蚁群算法在VRP问题中的应用研究[J].计算机工程与应用,2009,45(34):201-203. [16] Stützle T,Hoos H H.Max-min ant system[J].Future Generation Computer Systems,2000,16(19):889-914. [17] 耿耀华.基于MMAS的配送线路规划研究与应用[D].济南:山东大学,2008. An Improved MMAS for Vehicle Routing Problem XIE Li-ling,SONG Yan-bin,YANG Tan,LUO Qi-lun (School of Mathematics Sciences,South China Normal University,Guangzhou 510631,China) To exploit the best solutions found during an iteration or during the run of the algorithm,Max-Min Ant System (MMAS) allows the ant on the best solution to heighten the pheromone.Unfortunately,it will lead to the premature stagnation of the search.By analyzing the performance of MMAS in Vehicle Routing Problem (VRP),in order to avoid getting a local optimum solution,poor global search optimization ability,and slow convergence rate,a new strategy for pheromone updating is presented.It changes the value of the volatilization coefficients dynamically and updates the pheromones on the best ways,thus accelerating convergence and avoiding premature stagnation.The simulation experiments of the VRP show that the stability and convergence rate of the proposed algorithm is improved significantly compared with the basic MMAS. VRP;optimization algorithm;ant colony algorithm;MMAS;pheromone updating 2014-12-15 2015-03-21 时间:2016-02- 国家自然科学基金资助项目(11371154);广东省教育部产学研结合项目(2012B091100186) 谢骊玲(1977-),女,博士,副教授,研究方向为最优化算法与应用、物流与供应链管理。 http://www.cnki.net/kcms/detail/61.1450.TP.20160218.1619.006.html TP301.6 A 1673-629X(2016)03-0027-04 10.3969/j.issn.1673-629X.2016.03.0075 实验与结果


6 结束语

