基于自适应的粗糙C-均值聚类算法
严静静,张腾飞
(南京邮电大学 自动化学院,江苏 南京 210023)
基于自适应的粗糙C-均值聚类算法
严静静,张腾飞
(南京邮电大学 自动化学院,江苏 南京 210023)
粗糙C-均值的提出,首次将粗糙集与聚类算法结合起来。随后,众多学者对其进行了广泛研究。然而,绝大多数算法在研究簇的下近似、边界对象时,使用统一的权重,忽略了这些对象本身的差异性以及对所在簇的贡献。针对此问题,文中提出一种改进的聚类方法。通过样本对象偏移其所在簇心的程度,设定不同的簇偏移量,距离簇心越近的样本对象其簇偏移量越大,反之越小。通过此举以客观描述这些样本对象对其所在簇的贡献,使得最终聚类结果更加精确、簇内更加紧密、簇间更加稀疏。实例计算结果以及通过MATLAB对数据库中IRIS的数据集进行仿真验证,表明提出的改进算法具有一定的可行性。
聚类;粗糙集;粗糙C-均值;簇偏移量
1 概 述
聚类是满足同类对象相似而不同类对象差异的一种数据分类过程。通过优化对象函数,分组N个样本对象为c个可能的簇,实现簇内对象具有较高的相似性,簇间对象具有较低的相似性[1]。
传统的聚类技术强制划分数据对象到某个簇中,然而在许多数据挖掘应用中,这种要求过于局限。在某些情况下,数据对象可能属于两个或两个以上的簇。由此可知,类边界严重交叉重叠[2]。Bezdek提出模糊聚类如模糊C均值(FCM),定义0~1之间的模糊隶属度,使某个对象属于多个簇成为可能。2002年,Lingras[3-4]在Web数据挖掘时,把粗糙集理论融入到K-均值算法中,定义三种集合:上近似、下近似、边界。下近似中的对象一定属于所在的簇,上近似中的对象可能属于所在或者其他的簇,在解决边界重叠问题上具有一定的可行性。然而,Lingras在计算簇心时,只考虑了边界为空和边界非空的情况。当下近似为空时,算法会出现数值不稳定;计算对象是否属于上下近似时,使用绝对距离公式,忽视了存在的离散数据点。Peters[5]针对上(下)近似为空时,对相应的下(上)近似权重赋值为1;考虑到离散点的干扰,用相对距离代替绝对距离,并通过实例,证明其优势。文献[6-7]提出粗糙模糊算法和模糊粗糙算法,通过加入模糊隶属度,每个类有一个模糊下近似和模糊边界,下近似中的对象有明确的权重值,而边界对象有模糊的权重值,有效提高了边界精度。
上述粗糙C-均值算法在计算簇心时,上、下近似使用统一的权重值,忽视了样本对象内部的差异性。根据样本对象对其所在簇的贡献程度,无法使用一致的度量值来衡量,否则必将导致某些点的错误分类。
文中通过计算样本对象偏移簇心的程度,每个对象分别赋予不同的权重值,越是靠近簇心的样本对象其所在簇的权值越大,表明此对象对样本贡献最重。通过实验数据,对比不同的聚类算法,证明了文中提出算法的可行性。
2 粗糙C-均值聚类算法
2.1 粗糙C-均值聚类算法的基础

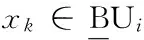
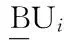
粗糙C-均值聚类算法流程如下:
步骤1:初始化参数,设置聚类个数c,任意选取c个样本中心Ci(i=1,2,…,c),距离阈值ε,权重值wl,wu。
步骤2:计算每个对象xk到簇心Ci(i=1,2,…,c)的欧氏距离。dik,djk为xk到簇心ci,cj的欧氏距离。

步骤4:更新簇心公式。
(1)
步骤5:重复步骤2~4,直到没有新的划分对象。
2.2 粗糙C-均值聚类算法的改进
文献[7]将模糊集的模糊隶属度加入到C-均值算法可以处理重叠问题,将粗糙集的上、下近似加入到C-均值算法可以定义不确定的、模糊的、不完备的类,改进后的算法能高效选取聚类原型。文献[8-13]提出粗糙模糊C均值融合算法。该算法通过粗糙集上、下近似的引入改变了模糊C均值算法中隶属度函数的分布情况,修正了模糊隶属度计算公式(2)和簇心的更新公式(3)。
模糊隶属度uik表明对象xk与类Ui的关联程度,隶属度越大表明对象对其类关联程度越高、簇作用越大。
(2)
将模糊隶属度加入粗糙集质心迭代公式:
Vi=
(3)
文献[6,8]将下近似中的对象的权重值设为1,认为下近似中的对象肯定是属于所在的类,对其类关联程度最高,簇心迭代公式更新为:
Vi=
(4)
3 基于自适应的粗糙K-均值聚类算法
3.1 对象偏移质心程度的偏移量
文中提出的算法(IMP-RCM)基于对象偏移簇心程度的偏移量,在进行公式迭代时,每个样本对象的权重值设为:
(5)
约束条件:
其中:σij为样本对象到簇心的标准差;mi为类i中样本数。
从式中可以看出类内对象离簇心越近,σij值越小,其对所在类的贡献越大,分配的权重值越大。反之,如果偏移度越大,σij样本对象到簇心距离越远,对其所在类的贡献越低,相应的样本对象获得的权重值越低。
对于wl与wu值的公式,文中不再使用默认参数值,而是参照样本中上、下近似对象的个数,wl(wu)是样本下(上)近似对象的个数比样本数。
(6)
3.2 基于自适应的粗糙C-均值聚类算法
文中提出的算法(IMP-RCM)是在式(4)的基础上进行改进。式(4)中簇内样本对象权重是所有样本总数的倒数,忽视样本个体对类的贡献差异。文中将式(5)引入到簇心迭代公式中。同时式(4)中wl、wu受初始参数影响较大,提出式(6),考虑上、下近似样本的对象个数。
步骤1:初始化参数,设置聚类个数c,任意选取c个样本中心Ci(i=1,2,…,c),距离阈值ε。
步骤2:计算权重值wl、wu,以及每个对象xk到样本中心Ci(i=1,2,…,c)的欧氏距离。dik,djk为xk到质心ci,cj的欧氏距离。

步骤4:更新簇心公式。
Vi=
(7)
步骤5:重复步骤2~4,直到没有新的划分对象。
在步骤4中,不再是传统意义上对象权重值都是固定值,在每次迭代过程中,簇心越来越收敛,趋于稳定。
4 实验仿真分析
为了验证算法的处理效果,文中对UCI数据库中的IRIS数据集进行MATLAB仿真分析。IRIS数据特征见表1。

表1 IRIS数据集特征
先通过主成分分析法将IRIS数据集进行降维处理,随后采用HCM算法、粗糙RCM算法、文中改进的RCM算法对降维后的数据集进行聚类分析。聚类分布图分别为图1~3所示。其中,▽、△、○分别表示IRIS的三个类对象,即簇1、簇2、簇3;黑圆×表示簇心。簇1相距簇2、簇3较远,而且簇2与簇3边界交叉重叠。
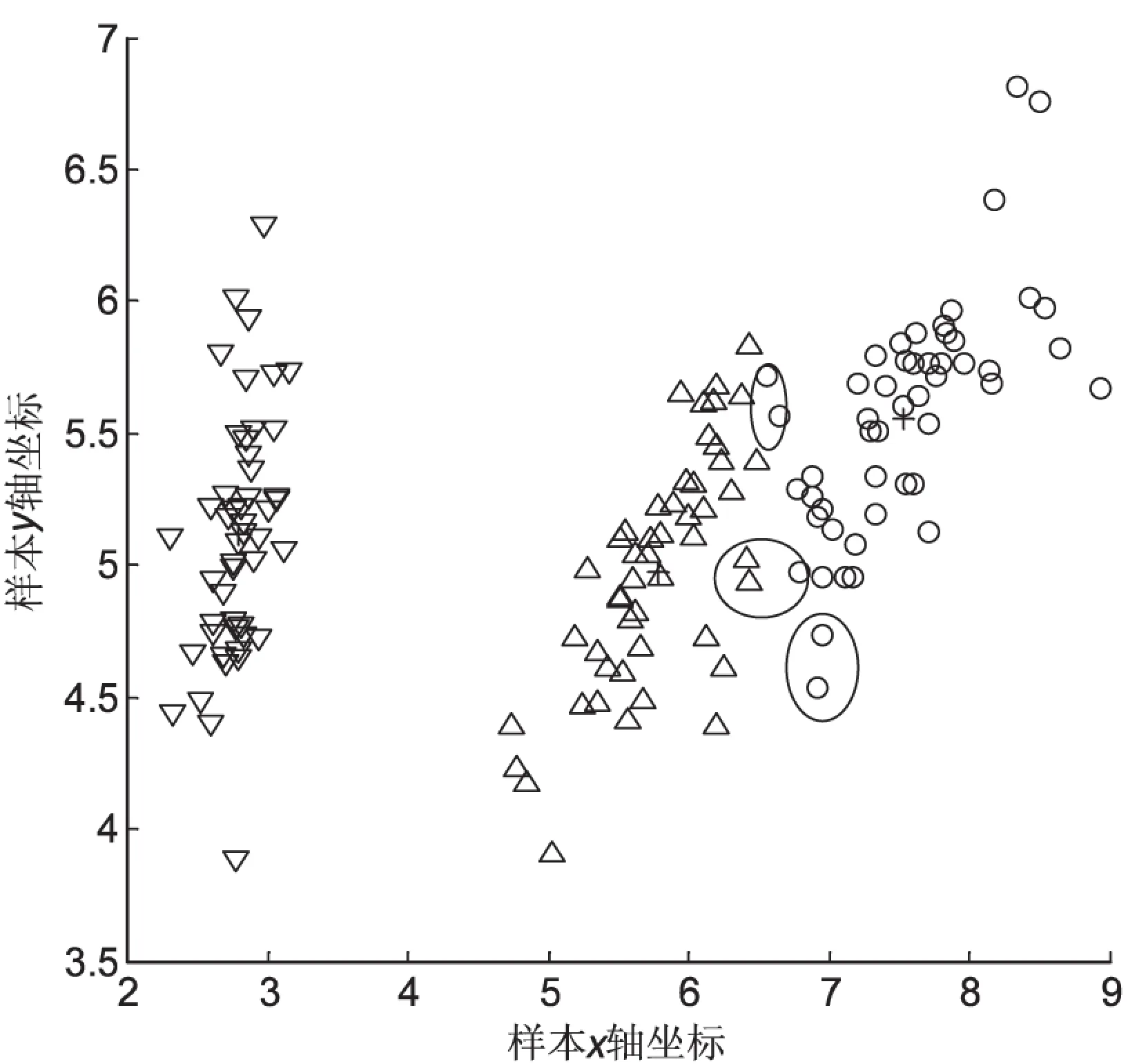
图1 HCM算法IRIS数据点分布
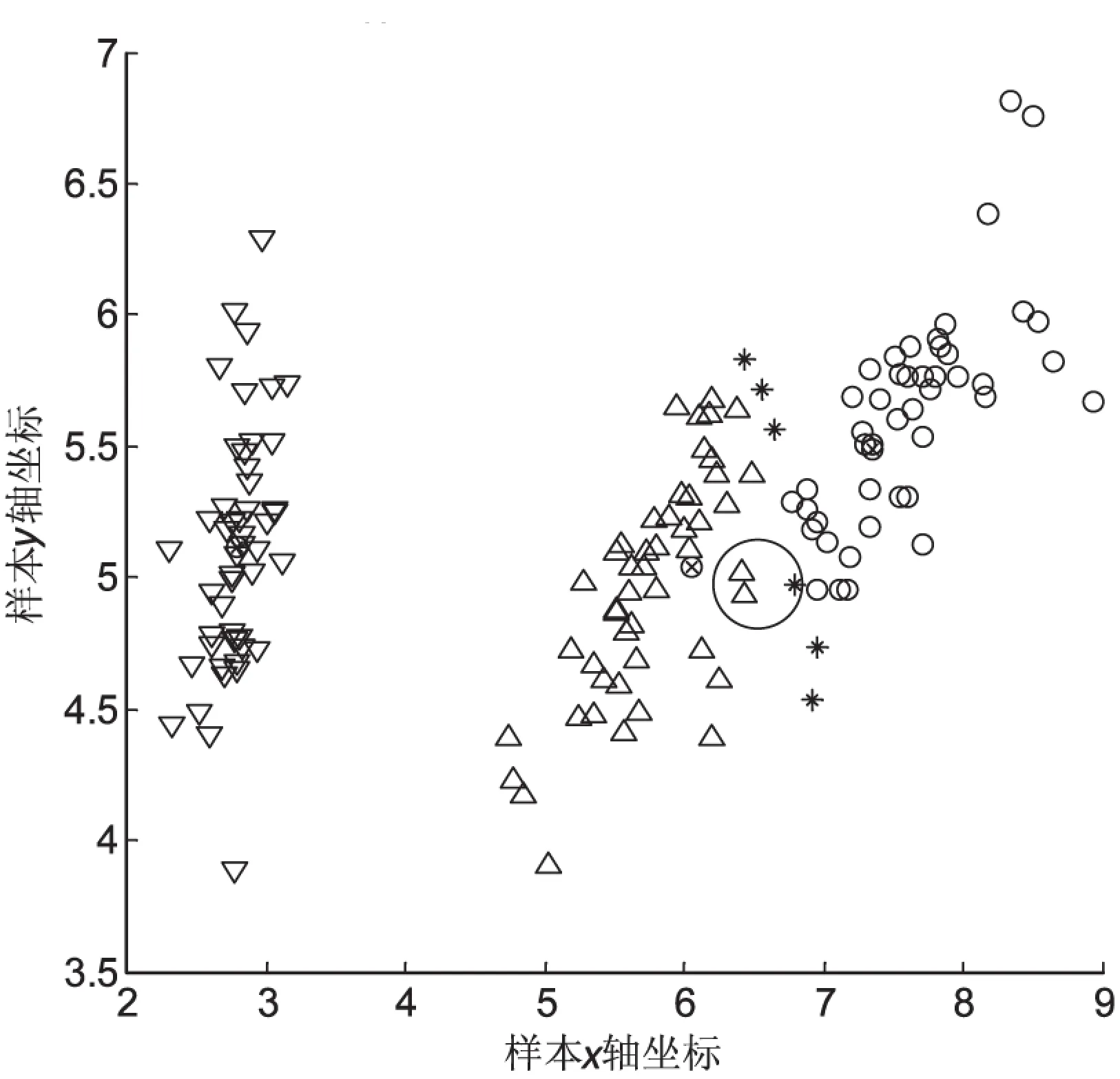
图2 RCM算法IRIS数据点分布
HCM算法强制认为非此即彼的划分,没有考虑边界严重交织、模糊的划分。图2标出有些点属于某个簇是不科学的;粗糙RCM的权重wl=0.7,wu=0.3。文中改进的权重值属于自适应值,从图2看出,出现划分的错误点,而改进算法得到的簇心(见图3)较图2更科学,与所在簇更紧密。
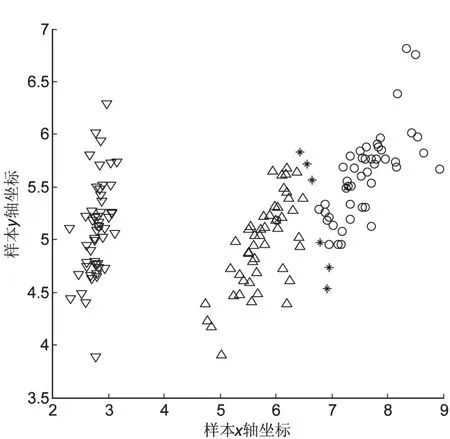
图3 文中改进的RCM算法IRIS数据点分布
5 结束语
文中主要针对绝大多数算法在研究簇的下近似、边界对象时,使用统一的权重,忽略了这些对象本身的差异性以及对所在簇的贡献差异,提出一种新的改进方法。通过对样本对象偏移其所在簇心的程度,设定不同的簇偏移量,以客观描述这些样本对象对其所在簇的贡献,使得最终聚类结果更加精确、簇内更加紧密、簇间更加稀疏。通过MATLAB仿真,对比以往的聚类,表明基于自适应的粗糙C-均值聚类算法的聚类效果更优。
[1]MitraS,BankaH,PedryczW.Rough-fuzzycollaborativeclustering[J].IEEETransonSystems,ManandCybernetics,PartB:Cybernetics,2006,36(4):795-805.
[2]LingrasP,PetersG.Roughclustering[J].WileyInterdisciplinaryReviews:DataMiningandKnowledgeDiscovery,2011,1
(1):64-72.
[3]LingrasP,WestC.Intervalsetclusteringofwebuserswithroughk-means[J].Journal of Intelligent Information Systems,2004,23(1):5-16.
[4] Pawan L,Rui Y,Chad W.Comparison of conventional and roughk-means clustering[C]//Proc of 9th international conference on rough sets,fuzzy sets,data mining,and granular computing.Berlin:Springer,2003:130-137.
[5] Georg P.Some refinements of roughk-means clustering[J].Pattern Recognition,2006,39(8):1481-1491.
[6] Hu Qinghua,Yu Daren.An improved clustering algorithm for information granulation[C]//Proc of 2nd international conference on FSKD.Berlin:Springer,2005:494-504.
[7] Maji P,Pal S K.RFCM:A hybrid clustering algorithm using rough and fuzzy sets[J].Fundamenta Informaticae,2007,80(4):475-496.
[8] 王 丹,吴孟达.粗糙模糊C均值融合聚类[J].国防科技大学学报,2011,33(3):145-150.
[9] Maji P,Paul S.Robust rough-fuzzy c-means algorithm:design and applications in coding and non-coding RNA expression data clustering[J].Fundamenta Informaticae,2013,124:153-174.
[10] Lai J Z C,Juan E Y T,Lai F J C.Rough clustering using generalized fuzzy clustering algorithm[J].Pattern Recognition,2013,46(9):2538-2547.
[11] Peters G,Crespo F,Lingras P,et al.Soft clustering - fuzzy and rough approaches and their extensions and derivatives[J].International Journal of Approximate Reasoning,2013,54(2):307-322.
[12] Scitovski R,Sabo K.Analysis of the k-means algorithm in the case of data points occurring on the border of two or more clusters[J].Knowledge-based Systems,2014,57(2):1-7.
[13] Velmurugan T.Performance based analysis between k-means and fuzzy c-means clustering algorithms for connection oriented telecommunication data[J].Applied Soft Computing,2014,19(6):134-146.
RoughC-means Clustering Algorithm Based on Self-adaption
YAN Jing-jing,ZHANG Teng-fei
(College of Automation,Nanjing University of Posts and Telecommunications,Nanjing 210023,China)
RoughC-meansisproposedtocombinetheroughsetwithclusteringalgorithmfirst.Inthefollowing,manyscholarshavebeendoingextensiveresearch.However,fortheobjectsinthelowapproximationorboundary,themostofalgorithmsuseunifiedweights,ignoringthedifferenceoftheobjectsthemselvesandthecontributiontotheclasses.Aimingatthisproblem,animprovedclusteringmethodisputforward.Basedondegreeofobjectsdeviatedcentroidofclusters,itsetsdifferentoffsetstohighlighttheseobjectsoncontributiontotheclassesinthispaper,makingtheresultofclusteringmoreprecise,intra-classesmoreclose,andinter-classesmoresparse.TheexperimentalresultsandsimulationverificationonIRISbyMATLABshowsthemethodisfeasible.
clustering;rough set;roughC-means;offsetsofclasses
2015-06-17
2015-09-23
时间:2016-02-18
江苏省普通高校研究生科研创新计划项目(46888LX14819)
严静静(1990-),女,硕士生,研究方向为模式识别与智能系统;张腾飞,副教授,博士,研究方向为智能信息处理、智能控制等。
http://www.cnki.net/kcms/detail/61.1450.TP.20160218.1634.054.html
TP
A
1673-629X(2016)03-0067-04
10.3969/j.issn.1673-629X.2016.03.016

