直升机横向漂浮稳定性时域分析方法与验证

段国贺，鲁 江

(1.中国直升机设计研究所，江西 景德镇 333001；2.中国船舶科学研究中心，江苏 无锡 214082)

直升机横向漂浮稳定性时域分析方法与验证

段国贺1，鲁 江2

(1.中国直升机设计研究所，江西 景德镇 333001；2.中国船舶科学研究中心，江苏 无锡 214082)

基于船舶横风横浪中倾覆概率衡准的时域数值计算方法，结合直升机的结构特点，考虑风倾力矩、波浪力和自由液面的影响，给出了一种直升机在随机波中横向漂浮稳定性时域分析方法，并利用试验数据对数值模型和计算结果进行了验证。

不规则波；时域分析；横向漂浮稳定性

0 引言

舰载直升机是以大型舰船为起降平台，主要在海面上空执行任务的直升机。为了保证人员和设备的安全，要求直升机具有水上漂浮能力，必须考虑直升机受到外界(波浪和风)大扰动时的横向稳定性。

《军用直升机飞行品质规范》(GJB902-90)对直升机水上漂浮时间和配平姿态有明确的要求。对具有在水上起飞和降落条件的直升机，旋翼停转后，直升机应能在水上漂浮2小时不致倾覆；对配有应急浮筒的直升机，当在水面降落旋翼停转后，直升机应能在水上漂浮5分钟不至倾覆。

按CCAR29R1和咨询通报AC29-C/D的相关要求，直升机应具备4级以上海况下大于5分钟的漂浮能力，并在应急浮囊一侧破损(一个应急浮囊隔舱)时具备至少2级海况的漂浮能力。

国外一些军机为保密等原因，需回收机体结构，所以在应急漂浮时间上有更为严格的指标，如：美军在H-46(CH-46的海军型)直升机应急漂浮装置的研制过程中，确定应急漂浮装置的两条基本性能要求：机身稳定漂浮10分钟，便于乘员撤离；机身漂浮3小时，便于机体回收。EH101军机应急漂浮装置研制中提出的指标为：在3级海况下，机身漂浮至少2小时。

1 漂浮稳定性衡准原则

漂浮特性是海上结构物必须研究的课题，针对船舶稳性，国内外进行了大量的研究，包括静稳性、规则波和不规则的非线性横摇响应，以及随机横浪中船舶倾覆概率的时域分析，理论和数值分析方法比较成熟。

船舶稳定性衡准分为静稳性衡准和动稳性衡准两种[1]。目前生效的《2008年完整稳性规则》，主要由静力学理论以海上结构物在静水中的复原力臂曲线的参数来描述的，并作为海上结构物抗倾覆能力的评估方法。该衡准是根据20世纪中期收集的海上结构物营运统计和气象衡准制定的规定性规则，主要是基于经验背景，无法体现海上结构物类型及其操作和环境条件的多样化，往往忽略影响舰船稳性的其它许多重要因素，例如外界扰动力、舰船运动的非线性阻尼等。而在研究随机风浪下舰船的大倾角横摇运动时，这些因素具有重要作用。同时目前生效的海上结构物横风横浪中抗倾覆能力的判断衡准，过于严格和保守，留出的安全裕度过大。

现行的确定性因素的稳性衡准难以合理地反映舰船的实际安全度，国际海事组织(IMO)于2014年开始执行第二代完整稳性衡准，即随机风浪中舰船的动稳性衡准。第二代衡准采用时域数值计算，通过随机非线性横摇运动参数的辨识和计算，得到舰船的稳性衡准值，通过横摇运动的分析计算，进行舰船稳性预报研究。

直升机海上漂浮稳定性的研究较少，理论和分析方法不够成熟，但是直升机和船舶在海面上漂浮时可同视为海上结构物，可以利用船舶漂浮稳定性的分析原理，结合直升机的结构特点，采用第二代稳性衡准规范，对直升机在海面上的漂浮稳定性进行数值预报和分析。

2 漂浮稳定性数值分析

2.1 静稳性

文献[2]利用船舶静稳性衡准方法对某带应急浮筒的直升机进行了横向漂浮稳定性计算，该方法建立在准静态的基础之上，根据静稳性曲线和动稳性曲线进行直升机稳性计算和校核，忽略了随机风浪下直升机的大倾角横摇运动时外界扰动力、运动的非线性阻尼等影响。

本文基于切片理论[3]，以重力与浮力平衡(等体积排水)及纵倾力矩为零为约束条件，通过迭代求解出直升机在不同横倾角度时的升沉位移和自由纵倾角，确定出直升机和水面的相对位置，同时考虑了各横剖面左右舷与波面存在一组或多组交点的情况，进而求出各浸水剖面面积和浮心位置，最后按照公式(1)进行积分，求得静水中复原力矩。重心、浮心位置关系示意图见图1。

(1)

式中:W—排水量；GZ—复原力臂；ρ—液体密度；g—重力加速度；L—机身长度；yB(x)—浸水横剖面中心在参考坐标系下的坐标；A(x)—各横剖面的浸水剖面面积。

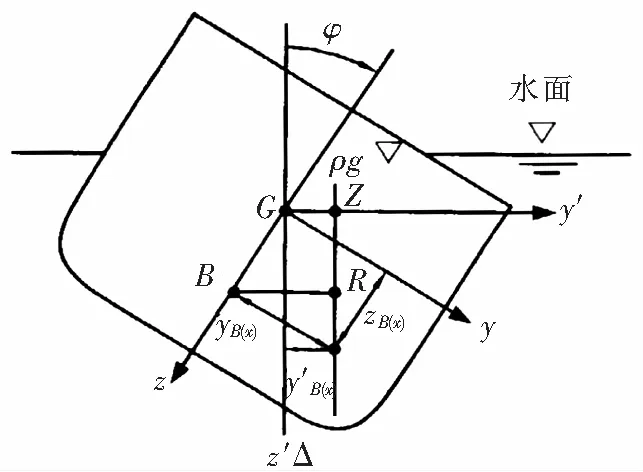
图1 重心、浮心位置关系示意图

由于本文分析的直升机带有浮筒，外形复杂且不同于常规的海洋结构物，在计算直升机的复原力臂时同时约束等体积排水和纵倾力矩为零时计算程序会不收敛，因此优先保证等体积排水的约束条件，即保持初始纵倾角不变，在不同横倾角时，通过调整吃水变化保证等体积排水。

2.2 单自由度横摇运动方程

直升机在横浪运动中，横摇运动和艏摇运动是耦合在一起的，因艏摇运动影响较小，可忽略艏摇运动，而横荡对横摇的耦合作用和横摇方向的绕射力矩互相抵消，波浪力只有Froude_Krylov力作用直升机[4]。田才福造等已经证明单自由度横摇方程可以近似表达横摇运动。

风浪并存时单自由度横摇运动方程如下：

(2)

方程两边同时除以惯性矩，方程无因次化后公式如下：

(3)

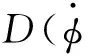
2.3 风压力

风压力矩采用下面公式计算：

(4)

其中：ρair:空气密度；Cm:抗力系数；Uw：定常风压力；U(t)：变动风压力；AL：机体受风投影面积；HC：风力作用力臂。

忽略其中比较小的变动风二次项部分，公式(4)可无因次化为：

(5)

其中：

(6)

(7)

不规则风中变动压力部分采用不同振幅和相位的正弦波叠加而成，公式如下：

(8)

其中：

(9)

变动风波谱采用Davenpot波谱，公式如下：

(10)

2.4 波浪力

入射波作用于机体的变动压力，其Froude_Krylov力可以根据有效波倾系数求出，公式如下：

(11)

上式无因次化为：

(12)

其中：γ:有效波倾系数；Θ(t):波形。

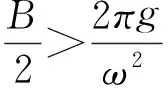
不规则波形采用不同振幅和相位的正弦波叠加而成，公式如下：

(13)

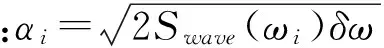
本文采用ITTC波谱，公式如下：

(14)

有义波高H1/3、平均波周期T01和平均风速UW存在对应函数关系：

(15)

(16)

本文参照公式(15)、(16)和《船舶原理》[5]中关于风速、浪级的定义对有义波高H1/3、平均波周期T01和平均风速UW进行取值。

2.5 横摇阻尼力

时域横摇数值计算中横摇衰减力采用线性阻尼系数和平方项阻尼系数，即：

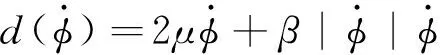
(17)

(18)

由于缺少自由横摇衰减曲线，同时该直升机规则波中横摇角度不大，本文采用等价线性阻尼系数，并通过直升机规则波中横摇响应曲线求出等价线性阻尼系数。

2.6 自由液面对稳性的影响

直升机的液舱，如燃油舱等，若舱内液体不满，则直升机倾斜时舱内的液体也将流向一侧，且保持与水面平行，这种可以自由移动的液面称为自由液面。自由液面的存在，降低了直升机的初稳性高，即提高了重心高度。

自由液面对直升机的初稳性高影响的计算公式如下：

(19)

其中：ix为自由液面的面积对其倾斜轴线的惯性矩；ρ为液体密度；g为重力加速度，P为直升机排水量。

由公式(19)看出，自由液面对初稳性高的修正值与自由液面的大小、直升机的排水量有关，一般与液舱内液体质量无关。

直升机带有若干个有自由液面的液舱时，可先算出各自的ρg·ix，然后把它们加起来除以排水量，便得到所有自由液面对初稳性高的修正值：

(20)

采用纵向隔舱壁可减小自由液面对稳性的影响，直升机油舱若采用横向舱壁，不能减小自由液面对稳性的影响，可认为整个油箱的液体只有一个自由液面。

3 数值预报算例及试验验证

为了验证该方法和软件在直升机漂浮稳定性分析上的适用性，对某型带浮筒直升机的横向漂浮能力进行了数值预报，并和水池试验结果做了比较，同时确定出合理的横摇阻尼系数和附加惯性矩。

3.1 直升机运动坐标系

采用右手坐标系(见图2)，说明如下：X=0平面在直升机机头顶点处；Y=0平面为直升机纵向对称面；Z=0平面为客/货舱地板下表面；X轴沿逆航向为正；Y轴沿航向右侧为正；Z轴垂直于X轴、Y轴向上为正。

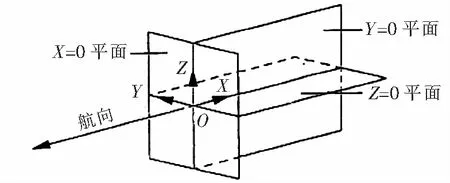
图2 直升机运动坐标系

3.2 直升机在静水中的浮态计算结果

直升机在静水中的浮态计算结果见表1。

表1 静水中浮态计算结果

3.3 静稳性曲线

根据上述静稳性计算方法，对某海上使用直升机进行了复原力矩的计算。为了验证该方法的有效性，计算结果和该直升机耐波性试验的数据[6]进行了对比，见图3-图5，计算与试验结果是比较接近的，主要差距来自于模型制造、试验测试精度以及计算未考虑纵倾角的影响。从图6可知，随着重量的减小，最大复原力矩减小，消失角随之减小，系因重心高度随着排水量减小而提高所致。

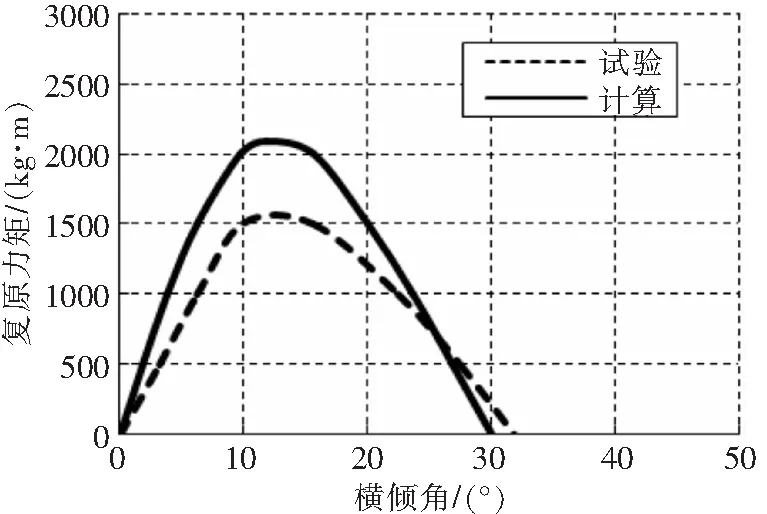
图3 静稳性曲线计算和试验对比(小重量)

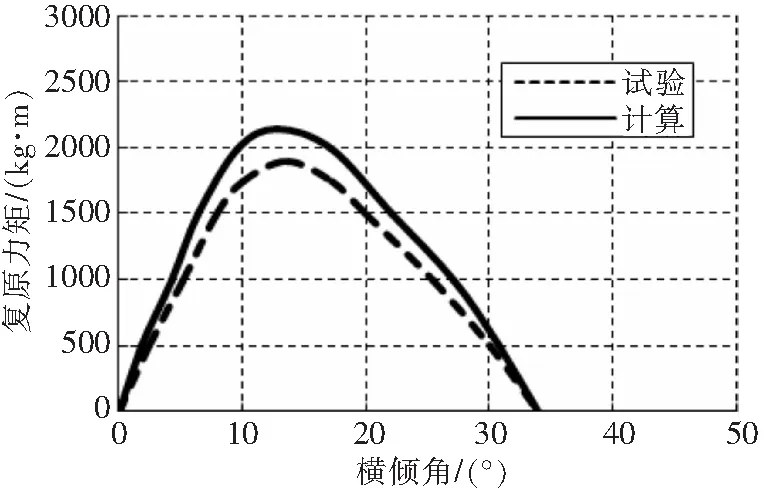
图4 静稳性曲线计算和试验对比(中等重量)

图5 静稳性曲线计算和试验对比(最大重量)

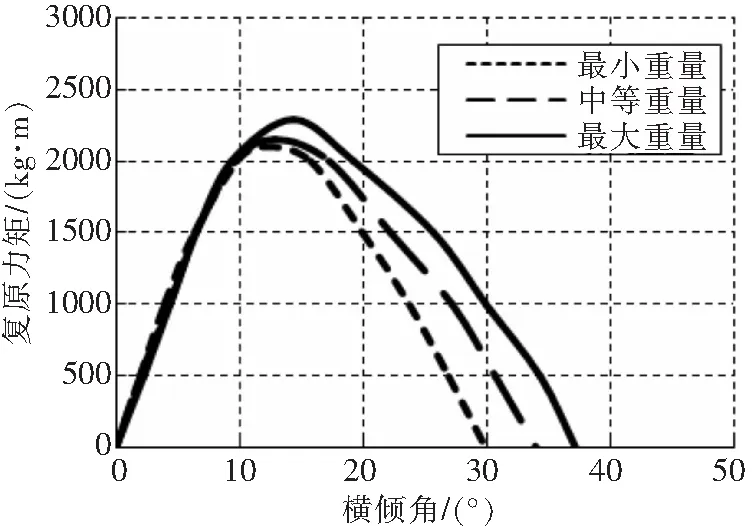
图6 静稳性曲线计算结果对比(重量变化)

自由液面修正前后的静稳性曲线对比如图7所示，考虑了燃油舱自由液面后，静稳性明显变差，按照横风横浪中抗倾覆能力的第一层判断衡准，考虑自由液面后，直升机的抗倾覆能力必然下降很多。自由液面的存在，降低了直升机的初稳性高，即提高了重心高度，但同时也改变了横摇固有周期，对横摇运动的影响需要通过实际计算其运动状态确定。

图7 液面修正对静稳性曲线的影响对比(计算)

3.4 规则波中横摇响应曲线

对某型直升机进行了规则波中的横摇响应计算，横摇响应曲线见图8-图10，计算结果稳定，和试验结果趋势一致，吻合较好，说明本文采用的数值计算方法是可行且准确的。该直升机初稳定高度较大，固有周期较短，当遇到周期较短的风浪时，将会发生共振，引起剧烈摇摆。从试验和计算数据看，基本在波长达20m左右时共振发生，此时共振周期为3～4s左右，横摇振幅最大达到30°/s。

同时计算了自由液面(燃油)修正对横摇响应曲线的影响。从图11可知，较小波长下横摇响应减小，但大波高时反而增大，虽然考虑自由液面后复原力矩减小，但由于运动并不是顺势增大或减小，所以其稳性性能还需进一步直接计算其在不规则波浪中的运动状态来确定。

图8 横摇振幅响应曲线(小重量)

图9 横摇振幅响应曲线(中等重量)

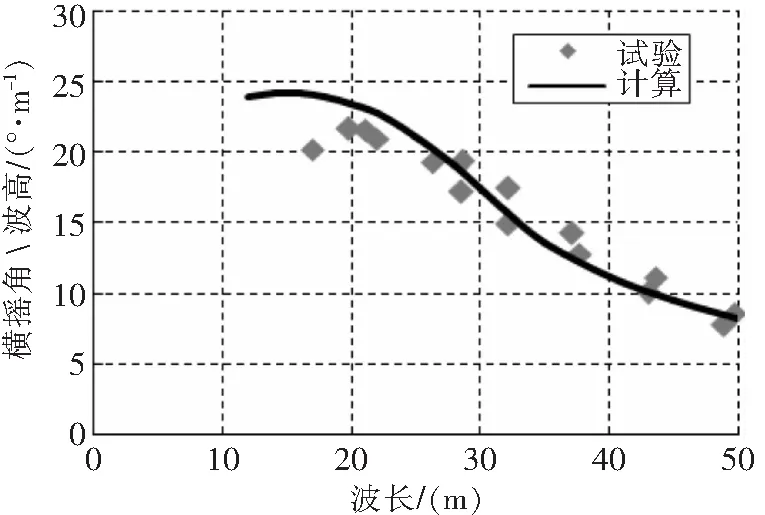
图10 横摇振幅响应曲线(最大重量)

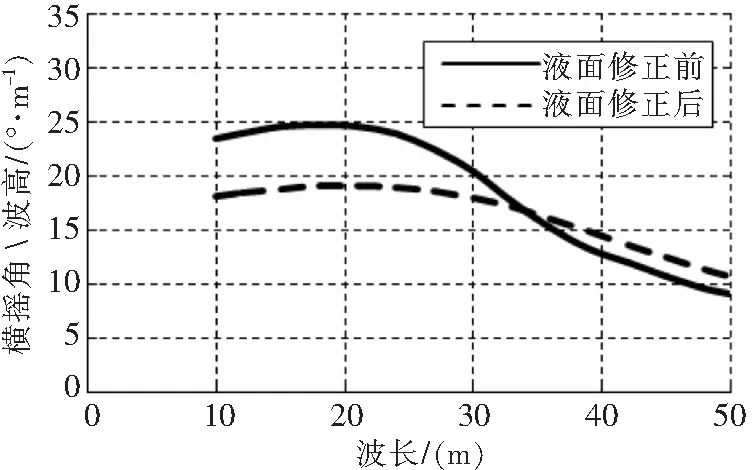
图11 液面修正对横摇振幅响应曲线影响对比

3.5 不规则波中横摇响应

采用时域分析方法进行直升机在不规则波中横摇响应计算，其中，横摇阻尼系数、横摇惯性矩和复原力矩采用规则波计算中的数值。图12给出了一组直升机时域横摇运动历程，描述了波形和横摇角随时间变化的历程，可以知道直升机最大横摇角或倾覆时对应的有义波高和时间点。

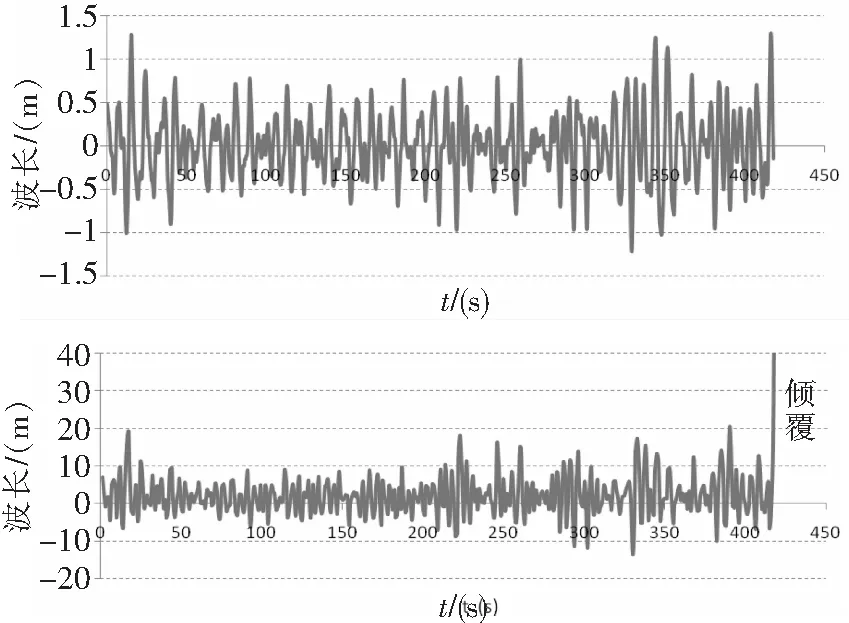
图12 不规则波中横摇响应时间历程对比(计算)

表2给出了不规则波中数值预报结果和试验结

果的对比，计算中采用和试验相同的有义波高和周期。判断直升机是否倾覆，计算中通常根据最大横摇角判断，而耐波性试验一般给出运动有义值，故现行数据只有直升机在不同海况下的有义值，故计算横摇角和试验不具备直接比较意义，但从其稳性情况可直接看出，试验中直升机在四级海况有风作用下是危险的，直接倾覆，无风时是安全的；而计算结果表明，直升机在四级海况有风作用下，只有波高达到一定高度时才倾覆，但总体结果是直升机在四级海况是有倾覆危险的。故本文的计算方法可以作为判断直升机稳性的一个依据，并具有一定的可靠性。

3.6 不规则波中横向漂浮稳定性预报结果

采用时域分析方法，对某直升机不规则波中横向漂浮稳定性进行了详细的计算分析，给出了抗风浪等级，不规则波数值预报结果见表3。

表2 不规则波中计算和试验结果对比

表3 不规则波计算结果

通过表3可以看出，该直升机随着重量的变小，稳定性变差。中等重量有义波高1.67(4级)时，两个小时之内稳定，最大横摇角21.8°；有义波高1.88(4级)时，5分钟之内稳定，最大横摇角19.4°，但在348秒时(5分钟48秒)倾覆；最小重量有义波高0.88(3级)时，两个小时之内稳定，最大横摇角14.9°；有义波高1.25(3、4级分界)时，5分钟之内稳定，最大横摇角15.1°，但在2652秒(约44分钟)时倾覆。

以前采用传统静稳定性分析方法评估该机具有2级海况的漂浮能力。

综上分析，该直升机具有3级海况的横向漂浮能力，4级海况倾覆，和试验结果基本一致；传统静稳定性分析方法过于严格和保守，留出的安全裕度过大。

4 结论

首次采用时域数值分析方法计算直升机漂浮稳定性，综合考虑了等价线性阻尼系数、自由液面修正以及随机横浪激励的影响，建立了横摇随机微分方程，采用数值分析方法求解微分方程模拟直升机的横摇倾覆过程，并对某型直升机进行了横向漂浮稳定性数值预报，结论如下：

1)时域数值分析方法突破了传统静稳定性分析方法忽略外界扰动力、运动的非线性阻尼和不规则波等因素，评估过于严格和保守，留出的安全裕度过大的局限性，可以对直升机横向漂浮能力进行更为精确的数值预报；

2)通过理论计算和试验结果相关性分析，静稳性曲线、规则波中横摇响应曲线以及不规则波中数值预报结果和试验趋势吻合较好，预报等级一致；

3)自由液面(燃油)的影响导致静稳性明显变差，但同时改变了横摇固有周期，较小波长下横摇响应减小，但大波高时反而增大，不规则波中数值预报结果和修正前基本一致；

4)通过数值预报分析，某型机具有3级海况的横向漂浮能力，4级海况倾覆。

[1] 王迎光，谭家华.对船舶完整稳性衡准的几点思考[J].船舶标准化工程师,2007,4.

[2] 汪正中.直升机水中横向稳性计算与试验验证[J].直升机技术,2012,4:1-7.

[3] 鲁 江，马 坤, 黄武刚.规则波中船舶复原力变化计算[J].武汉理工大学学报,2011. 35(5).

[4] 鲁 江，顾 民，马 坤, 黄武刚.随机波中船舶参数横摇研究[J].船舶力学,2012,8.

[5] 盛振邦，刘应中.船舶原理(下册)[M].上海：上海交通大学出版社，2004.

[6] 杨森华.某型机机耐波性试验报告[R].中国船舶科学研究中心科技报告,1982.

Analyzing Method and Validating in Time Domain on Transverse Stability of the Helicopter in Irregular

DUAN Guohe1, LU Jiang2

(1.China Helicopter Research and development Institute, Jingdezhen 333001, China; 2.China ship scientific Research Center, Wuxi 210482, Chnia)

This paper gave a analyzing method on transverse stability of the helicopter in irregular, based on the numerical account method of capsizing probability in time domain for ships in beam winds and waves, uniting the helicopter structure characteristic and considering the infection of the winds moment、wave force and free liquid.

irregular waves; analyzing in time domain; transverse stability

2015-09-08 作者简介：段国贺(1976-)，男，河南省驻马店市人，本科，高级工程师，主要研究方向：直升机飞行载荷及着水载荷。

1673-1220(2016)01-011-07

V212.12+1

A